Teil A
1
Gegeben ist die Funktion  mit maximaler Definitionsmenge
mit maximaler Definitionsmenge 
a)
Gib  sowie eine Gleichung der waagrechten Asymptote des Graphen von
sowie eine Gleichung der waagrechten Asymptote des Graphen von  an.
an.
(2 BE)
b)
Zeige, dass der Graph von  in genau einem Punkt eine waagrechte Tangente besitzt.
in genau einem Punkt eine waagrechte Tangente besitzt.
(3 BE)
2
Betrachtet werden die in  definierten Funktionen
definierten Funktionen  und
und  wobei
wobei  eine Stammfunktion von
eine Stammfunktion von  ist. Abbildung 1 zeigt den Graphen
ist. Abbildung 1 zeigt den Graphen  von
von 
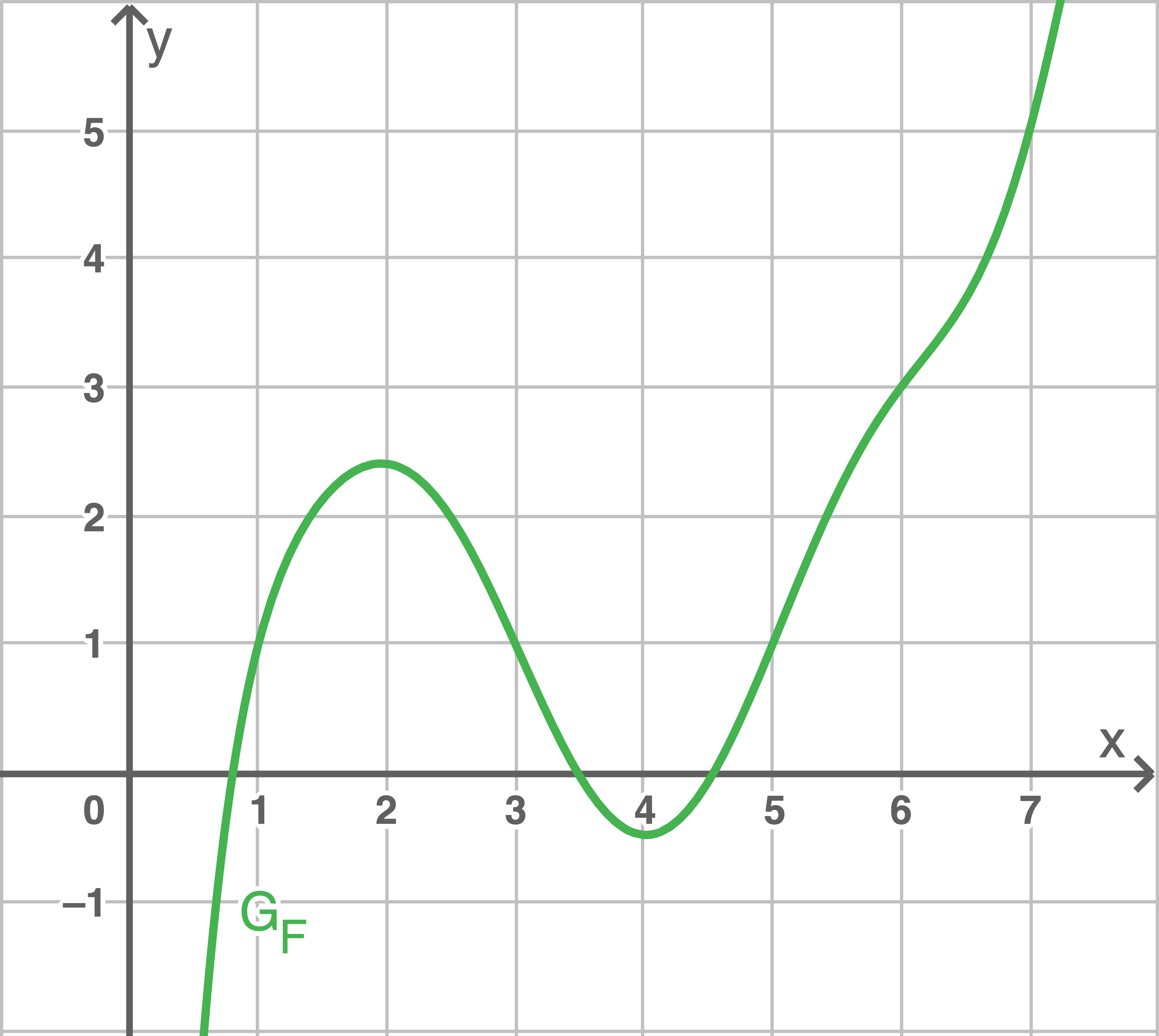
Abb. 1
a)
Bestimme den Wert des Integrals 
(2 BE)
b)
Bestimme den Funktionswert von  an der Stelle
an der Stelle  veranschauliche dein Vorgehen in Abbildung 1.
veranschauliche dein Vorgehen in Abbildung 1.
(3 BE)
3
a)
Gegeben ist die Funktion  mit Definitionsmenge
mit Definitionsmenge ![\(D_h = ]\frac{3}{2}; + \infty [.\)](https://mathjax.schullv.de/f69ea6759e496f56153418408498a78c2ac5f7e4435f8cd120fd6fc59deed645?color=5a5a5a) Gib die Nullstelle von
Gib die Nullstelle von  sowie einen Term der ersten Ableitungsfunktion von
sowie einen Term der ersten Ableitungsfunktion von  an.
an.
(2 BE)
b)
Die in  definierte Funktion
definierte Funktion  besitzt die Nullstelle
besitzt die Nullstelle  außerdem gilt
außerdem gilt  für alle
für alle  Abbildung 2 zeigt den Graphen
Abbildung 2 zeigt den Graphen  von
von 
Betrachtet wird die Funktion mit maximaler Definitionsmenge
mit maximaler Definitionsmenge 
Betrachtet wird die Funktion
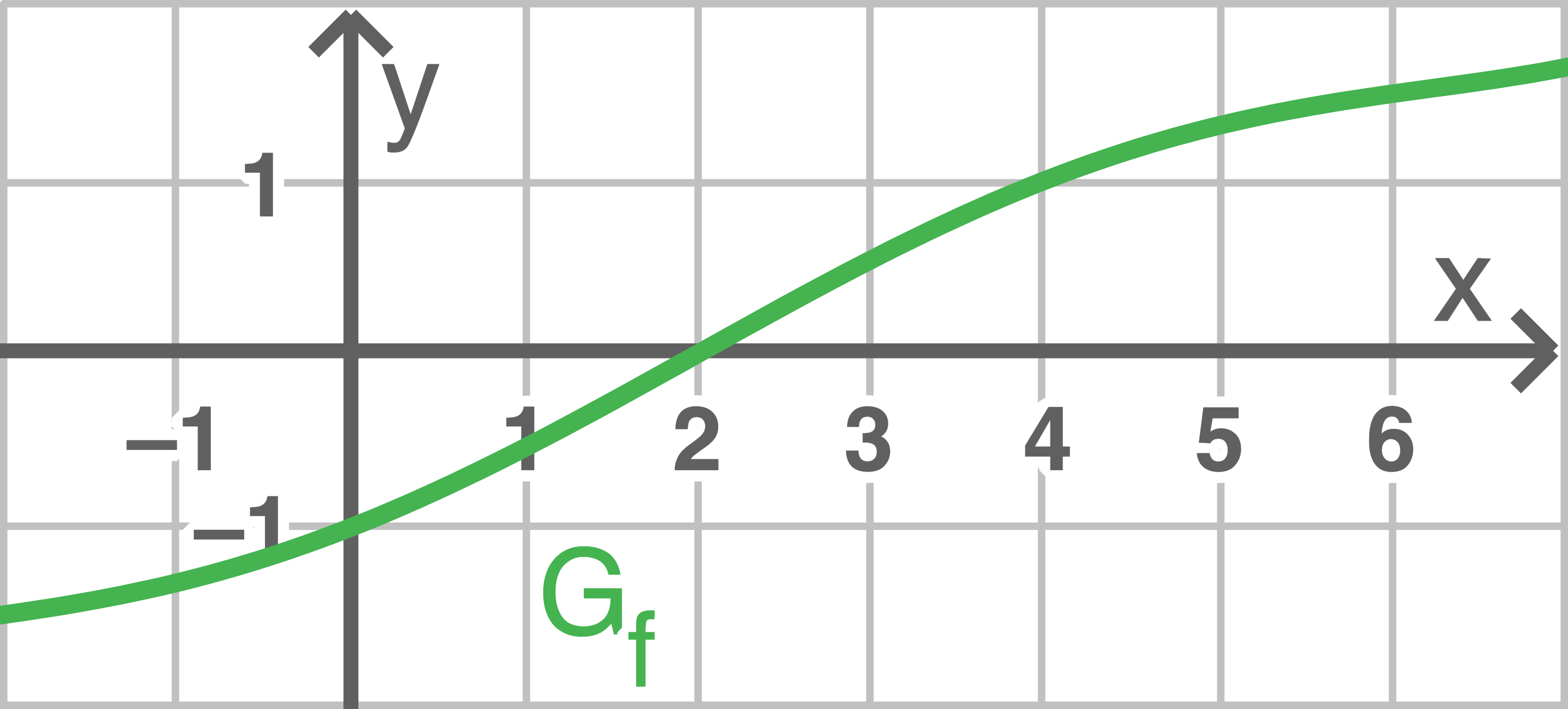
Abb. 2
(3 BE)
4
Gegeben sind die in  definierten Funktionen
definierten Funktionen  mit
mit  und
und 
a)
Zeige, dass  gilt.
gilt.
(1 BE)
b)
Betrachtet wird die Tangente an den Graphen von  im Punkt
im Punkt 
Bestimme diejenigen Werte von , für die diese Tangente eine positive Steigung hat und zudem die
, für die diese Tangente eine positive Steigung hat und zudem die  -Achse in einem Punkt schneidet, dessen
-Achse in einem Punkt schneidet, dessen  -Koordinate größer als
-Koordinate größer als  ist.
ist.
Bestimme diejenigen Werte von
(4 BE)
(20 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
2
a)
b)
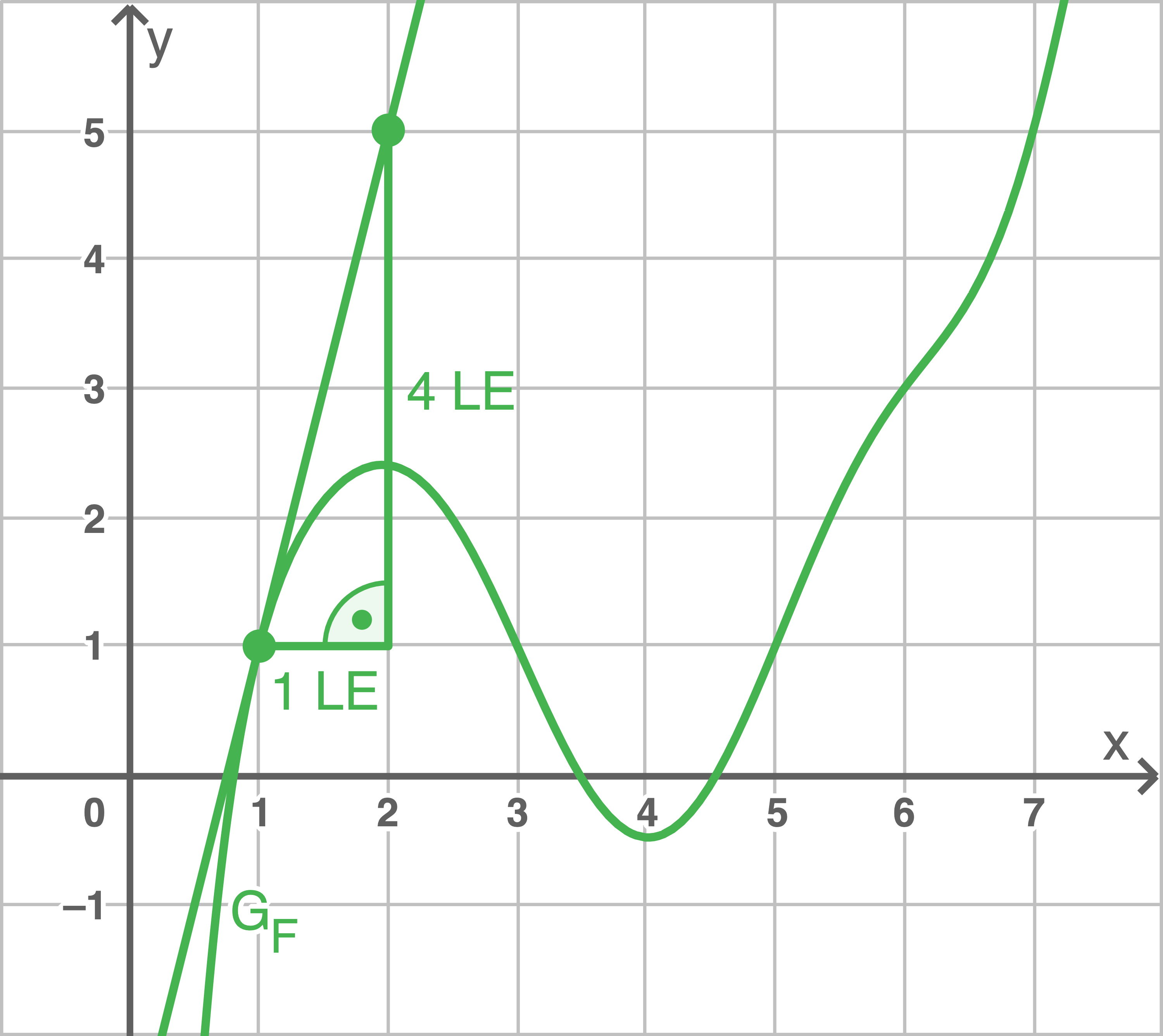
3
a)
Nullstelle angeben

 daher gilt:
daher gilt:


 Term der ersten Ableitungsfunktion angeben
Term der ersten Ableitungsfunktion angeben


b)
4
a)
b)