Teil B

Die Punkte $A( 6\mid0\mid4)$ , $B (0\mid6\mid4),$ $C(-6\mid0\mid4)$ und $D$ liegen in der Ebene $E$ und bilden die Eckpunkte der quadratischen Grundfläche einer Pyramide $ABCDS$ mit der Spitze $S( 0\mid0\mid1).$ $A, B$ und $S$ liegen in der Ebene $F.$

Zeige rechnerisch, dass das Dreieck $ABS$ gleichschenklig ist. Gib die Koordinaten des Punkts $D$ an und beschreibe die besondere Lage der Ebene $E$ im Koordinatensystem.

(4 BE)

Bestimme eine Gleichung der Ebene $F$ in Koordinatenform.
[zur Kontrolle: $F:x_1 + x_2 -2x_3 +2=0$ ]

(2 BE)

Berechne das Volumen $V$ der Pyramide $ABCDS.$

[zur Kontrolle: $V=72$ ]

(2 BE)

Mithilfe der folgenden beiden Gleichungen lässt sich die Größe eines Winkels $\epsilon$ berechnen:

I. $\cos \varphi = \dfrac{\,\bigg \vert \,\pmatrix{1\\1\\-2} \circ \pmatrix{0\\0\\1}\,\bigg \vert \,} {\,\bigg \vert \,\pmatrix{1\\1\\-2}\,\bigg \vert \,\cdot \,\bigg \vert \,\pmatrix{0\\0\\1}\,\bigg \vert \,}$

II. $\epsilon=(90°-\varphi )\cdot 2$

Beschreibe eine mögliche Bedeutung von $\epsilon$ im Zusammenhang mit der Pyramide.

(2 BE)

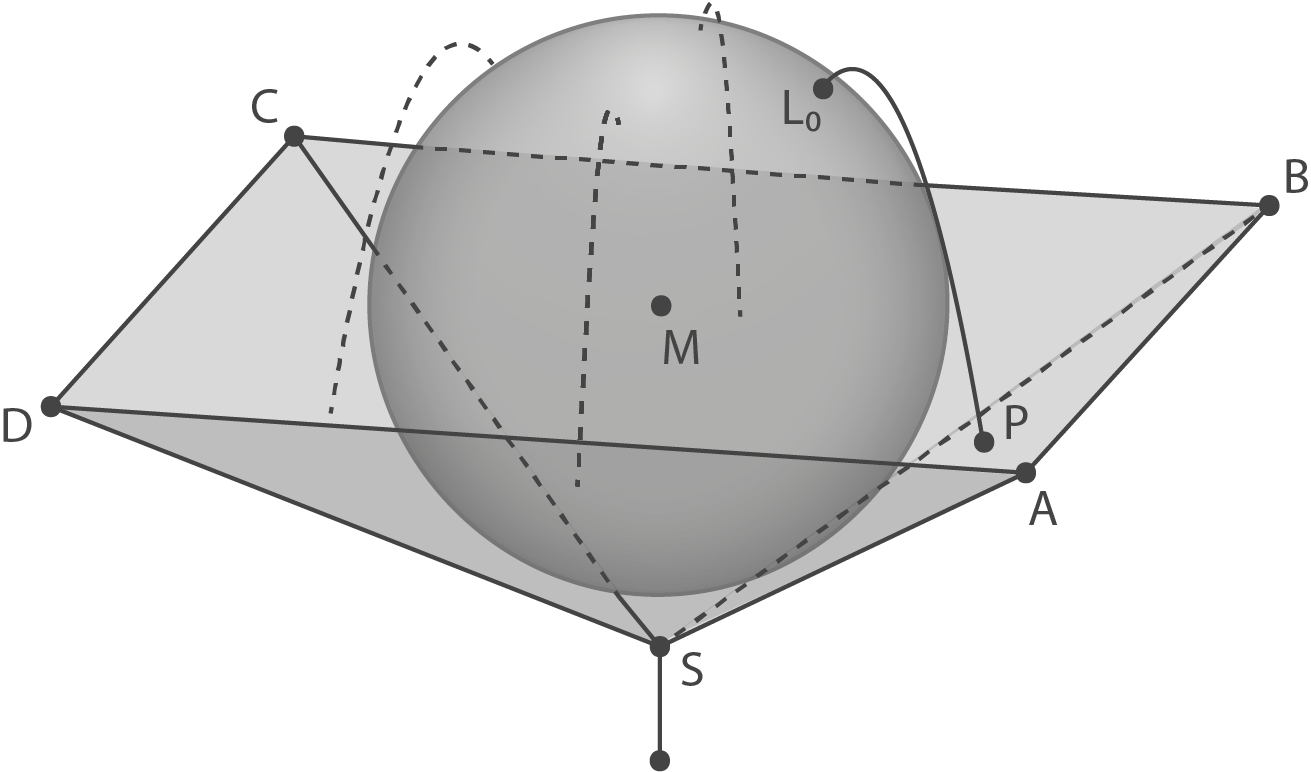
Ein auf einer Stange montierter Brunnen besteht aus einer Marmorkugel, die in einer Bronzeschale liegt. Die Marmorkugel berührt die vier Innenwände der Bronzeschale an jeweils genau einer Stelle. Die Bronzeschale wird im Modell durch die Seitenflächen der Pyramide $ABCDS$ beschrieben, die Marmorkugel durch eine Kugel mit Mittelpunkt $M( 0|0|4)$ und Radius $r$ . Die $x_1x_2-$ Ebene des Koordinatensystems stellt im Modell den horizontal verlaufenden Erdboden dar; eine Längeneinheit entspricht einem Dezimeter in der Realität.

Diagramm einer Kugel mit beschrifteten Punkten und Linien, die verschiedene geometrische Aspekte darstellen.

Ermittle den Durchmesser der Marmorkugel auf Zentimeter genau.
[zur Kontrolle: $r=\sqrt{6}$ ]

(4 BE)

Weise nach, dass der höchste Punkt des Brunnens ca. 64 cm über dem Erdboden liegt.

(2 BE)

Auf der Oberfläche der Marmorkugel treten an vier Stellen Wasserfontänen aus. Eine dieser Austrittsstellen wird im Modell durch den Punkt $L_0(1\mid 1\mid 6)$ beschrieben. Die zugehörige Fontäne wird modellhaft durch Punkte $L_t \bigg( t+1 \mid t+1\mid 6,2-5 \cdot (t-0,2)^2 \bigg)$ mit geeigneten Werten $t \in \mathbb{R}^+_0$ beschrieben.

Der Punkt $P$ liegt innerhalb des Dreiecks $ABS$ und beschreibt im Modell die Stelle, an der die Fontäne auf die Bronzeschale trifft (vgl. Abbildung). Bestimme die Koordinaten von $P.$

(3 BE)

Untersuche, ob der höchste Punkt der Wasserfontäne höher liegt als der höchste Punkt des Brunnens.

(2 BE)

Aus den vier Austrittsstellen fließen pro Sekunde insgesamt 80 ml Wasser in die Bronzeschale. Bestimme die Zeit in Sekunden, die vergeht, bis der anfangs leere Brunnen vollständig mit Wasser gefüllt ist.

(4 BE)

(25 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Gleichschenkliges Dreieck
Bei einem gleichschenkligen Dreieck sind zwei Seiten gleich lang.

Es gilt:
$d(A,S)= \left| \pmatrix{6-0\\0-0\\4-1} \right|$ $= \sqrt{6^2+3^2}=\sqrt{45}$

$d(B,S)= \left| \pmatrix{0-0\\6-0\\4-1} \right|$ $= \sqrt{6^2+3^2}=\sqrt{45}$

Da $d(A,S) = d(B,S)$ ist, sind die Seiten $\overline{AS}$ und $\overline{BS}$ des Dreiecks $ABS$ gleich lang und das Dreieck $ABS$ daher gleichschenklig.

Koordinaten von D
Da die Grundfläche quadratisch ist, ergeben sich die Koordinaten von $D$ zu $D(0\mid -6\mid 4).$

Besondere Lage von E
Die Ebene $E$ liegt parallel zur $x_1x_2-$ Ebene.

Zwei Spannvektoren der Ebene $F$ sind $\overrightarrow{AS}=\pmatrix{-6\\0\\-3}$ und $\overrightarrow{BS}=\pmatrix{0\\-6\\-3}.$

Ein Normalenvektor der Ebene ergibt sich mit dem Kreuzprodukt und dem crossP-Befehl des CAS:

$\overrightarrow{n_F}= \pmatrix{-6\\0\\-3} \times \pmatrix{0\\-6\\-3}$ $= \pmatrix{-18\\-18\\36 }$ $= -18 \cdot \pmatrix{1\\1\\-2}.$

Die Ebene lässt sich daraus in Koordinatenform aufstellen:

$\begin{array}[t]{rll} x_1+x_2-2x_3 +c&=& 0 &\quad \scriptsize \mid\; S \text{ einsetzen}\\[5pt] -2 \cdot 1 +c &=& 0 \\[5pt] c &=& 2 \\[5pt] \end{array}$

Somit lautet die Ebenengleichung von $F$ in Koordinatenform $x_1+x_2-2x_3+2=0.$

Die allgemeine Formel um das Volumen einer Pyramide zu berechnen, lautet $V_P=\dfrac{1}{3} \cdot G\cdot h.$

Die Höhe $h$ entspricht dem Abstand von $S$ zur Ebene $E.$ Da $E$ parallel zur $x_1x_2-$ Ebene liegt und zwar mit $x_3=4,$ beträgt der Abstand zu $S(0\mid 0\mid 1):$

$h = 4-1 =3\,\text{[LE]}$

Da die Grundfläche quadratisch ist, gilt:

$G= \left| \overrightarrow{AB} \right|^2$ $= \left| \pmatrix{-6\\6\\0} \right|^2= \sqrt{6^2+6^2}^2 =72\,\text{[FE]}$

Das Volumen der Pyramide ergibt sich zu

$V_P= \dfrac{1}{3} \cdot 72 \cdot 3 =72\,\text{[VE]}$

Der Winkel $\varphi$ ist der Winkel zwischen der Ebene $F$ und der $x_1x_2$ -Ebene, also der Winkel, in dem die Seitenflächen der Pyramide zur Horizontale bzw. zum Boden stehen.

Der Winkel $\epsilon = (90^{\circ}-\varphi)\cdot 2$ ist der Winkel, den zwei gegenüberliegende Seitenflächen innerhalb der Pyramide zusammen bilden.

Der Radius $r$ entspricht dem Abstand vom Mittelpunkt der Kugel zu den Seitenflächen, also beispielsweise dem Abstand von $M$ zur Ebene $F.$ Mit der Hesseschen Normalenform ergibt sich:

$\begin{array}[t]{rll} r&=& d(M;F) \\[5pt] &=&\left| \dfrac{0+0-2\cdot 4 +2}{\sqrt{1^2+1^2+(-2)^2}} \right| &\quad \scriptsize \\[5pt] &=&\left| \dfrac{-6}{\sqrt{6}} \right| &\quad \scriptsize \\[5pt] &=&\sqrt{6} \;\text{[dm]} \end{array}$

Für den Durchmesser folgt:

$d=2\cdot r= 2 \cdot \sqrt{6} \;\text{dm}$ $\approx 4,9\,\text{dm} \approx 49\;\text{cm}.$

Die Höhe des höchsten Punkts über dem Erdboden setzt sich zusammen aus

dem Abstand der Pyramidenspitze zum Erdboden, also der Abstand von $S$ zur $x_1x_2-$ Ebene: $d(S,x_1x_2) = 1\,\text{[dm]}$
dem Abstand von der Pyramidenspitze zum Mittelpunkt der Kugel, also: $d(M,S) = 4-1 =3\,\text{[dm]}$
dem Abstand vom Mittelpunkt der Kugel zum höchsten Punkt der Kugel, also dem Radius $r = \sqrt{6}\approx 2,4\,\text{[dm]}$ .

Insgesamt ergibt sich damit für den Abstand des höchsten Punkts vom Erdboden:

$d\approx 1\,\text{dm} + 3\,\text{dm} + 2,4\,\text{dm}$ $= 6,4\,\text{dm} = 64\,\text{cm}$

$P$ ist einer der Punkte $L_t$ und liegt in der Ebene $F.$ Die Koordinaten von $L_t$ werden in die Koordinatengleichung von $F$ eingesetzt. Mit dem solve-Befehl des CAS ergibt sich:

Rechenweg anzeigen

$\begin{array}[t]{rll} t_{1}&=&-\dfrac{4}{5} \\[5pt] t_{2}&=& 1 \\[5pt] \end{array}$

Da $t\in \mathbb{R}^+_0$ vorgegeben ist, wird $t_2=1$ in die Koordinaten von $L_t$ eingesetzt und ergibt:

$L_1 = P(2 \mid 2 \mid 3)$

Der höchste Punkt der Wasserfontäne ergibt sich aus der $x_3$ -Koordinate von $L_t.$ Die $x_3$ -Koordninate entspricht einer quadratischen Funktion, aus der der Scheitelpunkt abgelesen werden kann. Der Scheitelpunkt ist $S(0,2 \mid 6,2),$ wobei der Wert der $y$ -Koordinate der Höhe über dem Erdboden entspricht.
Somit liegt der höchste Punkt der Wasserfontäne auf $62 \;\text{cm}$ über dem Erdboden und folglich unter dem höchsten Punkt des Brunnens mit $64 \;\text{cm}.$

Um die Zeit zu bestimmen muss zunächst das Volumen, welches vom Wasser eingenommen wird, bestimmt werden.

Berechnung des Volumens anzeigen

$V_{\text{Wasser}} \approx 41.219 \;\text{ml}$

Folglich ist der anfangs leere Brunnen nach $\dfrac{41.219\,\text{ml}}{80 \frac{\text{ml}}{\text{s}}} \approx 515 \;\text{s}$ vollständig mit Wasser gefüllt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?