Geometrie Prüfungsteil B
Aufgabengruppe 1
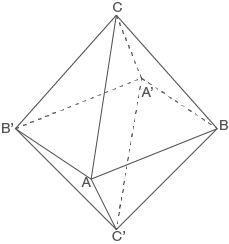
In einem kartesischen Koordinatensystem legen die Punkte  ,
,  und
und  das gleichseitige Dreieck
das gleichseitige Dreieck  fest.
fest.
a)
Ermittle eine Gleichung der Ebene  , in der das Dreieck
, in der das Dreieck  liegt, in Normalenform.
liegt, in Normalenform.
Spiegelt man die Punkte
(mögliches Ergebnis:  )
)
(3P)
b)
Beschreibe die Lage der Ebene, in der die Punkte  und
und  liegen, im Koordinatensystem. Zeige, dass die Strecke
liegen, im Koordinatensystem. Zeige, dass die Strecke ![\([CC‘]\)](https://mathjax.schullv.de/fa164b6e9cc4fb3d981051d34a653352a5075c84d0f23d6834e49c9b7f2396bb?color=5a5a5a) senkrecht auf dieser Ebene steht.
senkrecht auf dieser Ebene steht.
(3P)
c)
Begründe, dass das Viereck  ein Quadrat mit der Seitenlänge
ein Quadrat mit der Seitenlänge  ist.
ist.
(4P)
d)
Berechne den Abstand des Punkts  von der Ebene
von der Ebene  .
.
(2P)
Der Körper  ist ein sogenanntes Oktaeder. Er besteht aus zwei Pyramiden mit dem Quadrat
ist ein sogenanntes Oktaeder. Er besteht aus zwei Pyramiden mit dem Quadrat  als gemeinsamer Grundfläche und den Pyramidenspitzen
als gemeinsamer Grundfläche und den Pyramidenspitzen  bzw.
bzw.  .
.
e)
Weise nach, dass das Oktaeder das Volumen  besitzt.
besitzt.
(2P)
f)
Bestimme die Größe des Winkels zwischen den Seitenflächen  und
und  .
.
(3P)
g)
Alle Eckpunkte des Oktaeders liegen auf einer Kugel. Gib eine Gleichung dieser Kugel an.
Berechne den Anteil des Oktaedervolumens am Kugelvolumen.
Berechne den Anteil des Oktaedervolumens am Kugelvolumen.
(3P)
(20P)
Aufgabengruppe 2
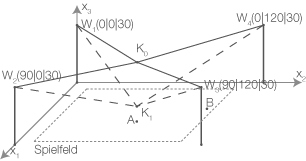
Für die Fernsehübertragung eines Fußballspiels wird über dem Spielfeld eine bewegliche Kamera installiert. Ein Seilzugsystem, das an vier Masten befestigt wird, hält die Kamera in der gewünschten Position. Seilwinden, welche die Seile koordiniert verkürzen und verlängern, ermöglichen eine Bewegung der Kamera.
In der Abbildung ist das horizontale Spielfeld modellhaft als Rechteck in der -Ebene eines kartesischen Koordinatensystems dargestellt. Die Punkte
-Ebene eines kartesischen Koordinatensystems dargestellt. Die Punkte  und
und  beschreiben die Positionen der vier Seilwinden. Eine Längeneinheit im Koordinatensystem entspricht
beschreiben die Positionen der vier Seilwinden. Eine Längeneinheit im Koordinatensystem entspricht  in der Realität, d.h. alle vier Seilwinden sind in einer Höhe von
in der Realität, d.h. alle vier Seilwinden sind in einer Höhe von  angebracht.
Der Punkt
angebracht.
Der Punkt  beschreibt die Lage des Anstoßpunkts auf dem Spielfeld. Die Kamera befindet sich zunächst in einer Höhe von
beschreibt die Lage des Anstoßpunkts auf dem Spielfeld. Die Kamera befindet sich zunächst in einer Höhe von  vertikal über dem Anstoßpunkt. Um den Anstoß zu filmen, wird die Kamera um
vertikal über dem Anstoßpunkt. Um den Anstoß zu filmen, wird die Kamera um  vertikal abgesenkt. In der Abbildung ist die ursprüngliche Kameraposition durch den Punkt
vertikal abgesenkt. In der Abbildung ist die ursprüngliche Kameraposition durch den Punkt  , die abgesenkte Position durch den Punkt
, die abgesenkte Position durch den Punkt  dargestellt.
dargestellt.
In der Abbildung ist das horizontale Spielfeld modellhaft als Rechteck in der
a)
Berechne die Seillänge, die von jeder der vier Seilwinden abgerollt werden muss, um dieses Absenken zu ermöglichen, wenn man davon ausgeht, dass die Seile geradlinig verlaufen.
(4P)
b)
Berechne die Größe des Winkels, den das Seilstück, das im Modell durch die Strecke ![\([W_1K_1]\)](https://mathjax.schullv.de/55b9ea0aae3a18a0ca595881788c288579f3022fc4aa626fffac866fb3c34772?color=5a5a5a) beschrieben wird, mit der Horizontalen einschließt.
beschrieben wird, mit der Horizontalen einschließt.
(2P)
c)
Bestimme die Koordinaten von  .
.
(Ergebnis:  )
)
(3P)
d)
Im Zielpunkt ist die Kamera zunächst senkrecht nach unten orientiert. Um die Position des Balls anzuvisieren, die im Modell durch den Punkt  beschrieben wird, muss die Kamera gedreht werden. Berechne die Größe des erforderlichen Drehwinkels.
beschrieben wird, muss die Kamera gedreht werden. Berechne die Größe des erforderlichen Drehwinkels.
Der Torwart führt den Abstoß aus. Der höchste Punkt der Flugbahn des Balls wird im Modell durch den Punkt
(3P)
e)
Ermittle eine Gleichung der durch die Punkte  und
und  festgelegten Ebene
festgelegten Ebene  in Normalenform und weise nach, dass
in Normalenform und weise nach, dass  unterhalb von
unterhalb von  liegt.
liegt.
(Mögliches Teilergebnis:  )
)
(7P)
f)
Mache plausibel, dass folgende allgemeine Schlussfolgerung falsch ist: „Liegen der Startpunkt und der anvisierte höchste Punkt einer Flugbahn des Balls im Modell unterhalb der Ebene  , so kann der Ball entlang seiner Bahn die Seile, die durch
, so kann der Ball entlang seiner Bahn die Seile, die durch ![\([W_1K_2]\)](https://mathjax.schullv.de/ac5720d75fbadde194f3132aa09f1a72ccf3fe18dabe37051fb56dd1d84d7ca2?color=5a5a5a) und
und ![\([W_2K_2]\)](https://mathjax.schullv.de/4c698bffcd575ffe5f1f190ca62e038a941dd745bbe71b68744ca0ca9b8888f4?color=5a5a5a) beschrieben werden, nicht berühren.“
beschrieben werden, nicht berühren.“
Bildnachweise [nach oben]
(2P)
(20P)
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabengruppe 1
 Normalenform aufstellen
Du sollst die Normalenform der Ebene
Normalenform aufstellen
Du sollst die Normalenform der Ebene  durch die drei Punkte
durch die drei Punkte  ,
,  ,
,  bestimmen. Die Normalenform erhältst du durch
bestimmen. Die Normalenform erhältst du durch
 Dabei bezeichnet
Dabei bezeichnet  den Stützvektor und
den Stützvektor und  den Normalenvektor, welcher senkrecht auf den zwei Spannvektoren steht.
Benutze
den Normalenvektor, welcher senkrecht auf den zwei Spannvektoren steht.
Benutze  als Ausgangspunkt der Ebene und als Spannvektoren
als Ausgangspunkt der Ebene und als Spannvektoren  und
und  .
1. Schritt: Spannvektoren berechnen
Die Spannvektoren entsprechen dem Vektor zwischen
.
1. Schritt: Spannvektoren berechnen
Die Spannvektoren entsprechen dem Vektor zwischen  und
und  bzw.
bzw.  und
und  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=& \vec B-\vec A \\[5pt]
&=&\pmatrix{3 \\ 6 \\ 3}-\pmatrix{6 \\ 3 \\ 3} \\[5pt]
&=&\pmatrix{-3\\3\\0}
\end{array}\)](https://mathjax.schullv.de/7af650ed19f75e4c11011791fd5b3c5a08f299062b96c3741ad985b855d6b0bb?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{AC}&=& \vec C-\vec A \\[5pt]
&=&\pmatrix{3 \\ 3 \\ 6}-\pmatrix{6 \\ 3 \\ 3} \\[5pt]
&=&\pmatrix{-3\\0\\3}
\end{array}\)](https://mathjax.schullv.de/c86e30403a16954aaa217f8b7c2f997e4072d07005fa8ff7ee16fbc6aab1c77c?color=5a5a5a) 2. Schritt: Normalenvektor berechnen
Mit dem Kreuzprodukt kannst du den Normalenvektor bestimmen, den Befehl findest du unter:
2. Schritt: Normalenvektor berechnen
Mit dem Kreuzprodukt kannst du den Normalenvektor bestimmen, den Befehl findest du unter:
 Abb. 1: Kreuzprodukt mit dem nspire berechnen
Du erhältst das Kreuzprodukt
Abb. 1: Kreuzprodukt mit dem nspire berechnen
Du erhältst das Kreuzprodukt  . Für eine Ebene kannst du auch ein Vielfaches des Normalenvektors verwenden. Dies ermöglicht es dir Ebenengleichungen zu vereinfachen. Für die Normalenform erhältst du:
. Für eine Ebene kannst du auch ein Vielfaches des Normalenvektors verwenden. Dies ermöglicht es dir Ebenengleichungen zu vereinfachen. Für die Normalenform erhältst du:
![\(\begin{array}[t]{rll}
E : & 1\cdot x_1+1\cdot x_2+1\cdot x_3=d & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ecd5fb128303ca9a27f967c140ff05120a4e220d53353ea8da4f19938c645d9e?color=5a5a5a) Die Konstante
Die Konstante  bestimmst du durch Einsetzen eines Punktes, welcher sicher in der Ebene liegt. Dazu verwendest du den Stützpunkt
bestimmst du durch Einsetzen eines Punktes, welcher sicher in der Ebene liegt. Dazu verwendest du den Stützpunkt  .
.
![\(\begin{array}[t]{rll}
d&=& 6+3+3 \\[5pt]
&=& 12
\end{array}\)](https://mathjax.schullv.de/b4afb1be8b6cec976f3bf3a01d752685e6476c547b95e8ee663a1a4627852e63?color=5a5a5a) Du erhältst die Normalenform der Ebene mit:
Du erhältst die Normalenform der Ebene mit:
![\(\begin{array}[t]{rll}
E : & 1\cdot x_1+1\cdot x_2+1\cdot x_3=12 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d34e381e24aa65cb5b5c1508ec059649f53efb4b498310c37964e7ad7f1a5212?color=5a5a5a)
 Lage der Ebene beschreiben
Du sollst die Lage der Ebene durch die drei Punkte
Lage der Ebene beschreiben
Du sollst die Lage der Ebene durch die drei Punkte  ,
,  und
und  beschreiben. Aller drei Punkte besitzen die gleiche
beschreiben. Aller drei Punkte besitzen die gleiche  -Koordinate.
Somit liegen die Punkte in einer mit dem Abstand
-Koordinate.
Somit liegen die Punkte in einer mit dem Abstand  zur
zur  -Ebene parallelen Ebene.
-Ebene parallelen Ebene.

 senkrecht zur Ebene nachweisen
Du sollst nachweisen, dass die Strecke bzw. der Vektor
senkrecht zur Ebene nachweisen
Du sollst nachweisen, dass die Strecke bzw. der Vektor  senkrecht zur Ebene ist. Dazu bestimmst du zuerst die Koordinaten von
senkrecht zur Ebene ist. Dazu bestimmst du zuerst die Koordinaten von  .
1. Schritt: Koordinaten von
.
1. Schritt: Koordinaten von  bestimmen
bestimmen
 entsteht durch Spiegelung von
entsteht durch Spiegelung von  an
an  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{C‘}&=& 2\cdot \overrightarrow{CZ}+\overrightarrow{C} \\[5pt]
&=& 2\cdot \left( \overrightarrow{Z}-\overrightarrow{C} \right)+\overrightarrow{C} \\[5pt]
&=& 2\cdot \left( \pmatrix{3\\3\\3}-\pmatrix{3\\3\\6}\right)+\pmatrix{3\\3\\6} \\[5pt]
&=& 2\cdot \pmatrix{0\\0\\-3}+\pmatrix{3\\3\\6} \\[5pt]
&=& \pmatrix{3\\3\\0}
\end{array}\)](https://mathjax.schullv.de/f4cb9c01eaa6013f82def2626fa97ab945d84599f0a23256497f99b39c5aef01?color=5a5a5a) 2. Schritt:
2. Schritt:  bestimmen
Desweiteren wird der Vektor
bestimmen
Desweiteren wird der Vektor  benötigt.
benötigt.
![\(\begin{array}[t]{rll}
\overrightarrow{CC‘}&=& \overrightarrow{C‘}-\overrightarrow{C} \\[5pt]
&=& \pmatrix{3\\3\\0}-\pmatrix{3\\3\\6} \\[5pt]
&=& \pmatrix{0\\0\\-6}
\end{array}\)](https://mathjax.schullv.de/0c9fce91f5701aaeace336988503b5ed7ded42c184094306fa65eab0fa0d556f?color=5a5a5a) 3. Schritt: Senkrecht nachweisen
Vektoren welche senkrecht zu einer Ebene stehen sind Vielfache des Normalenvektors. Da die Ebene parallel zur
3. Schritt: Senkrecht nachweisen
Vektoren welche senkrecht zu einer Ebene stehen sind Vielfache des Normalenvektors. Da die Ebene parallel zur  -Ebene ist, ist ihr Normalenvektor
-Ebene ist, ist ihr Normalenvektor  . Es muss somit ein
. Es muss somit ein  geben, dass gilt:
geben, dass gilt:
![\(\begin{array}[t]{rll}
\pmatrix{0\\0\\-6}&=& \lambda\cdot \pmatrix{0\\0\\1} \\[5pt]
\lambda&=& -6
\end{array}\)](https://mathjax.schullv.de/e965baf9de8fd30279c1e4333e7685ef9639f837b9be87ae57d47145ce942e9e?color=5a5a5a) Da ein
Da ein  existiert, steht
existiert, steht  senkrecht auf der Ebene.
senkrecht auf der Ebene.
 Seitenlänge des Quadrats begründen
Du sollst begründen, dass es sich bei dem Viereck
Seitenlänge des Quadrats begründen
Du sollst begründen, dass es sich bei dem Viereck  um ein Quadrat mit Seitenlänge
um ein Quadrat mit Seitenlänge  handelt. Bestimme zuerst die Koordinaten von
handelt. Bestimme zuerst die Koordinaten von  und
und  .
1. Schritt: Koordinaten von
.
1. Schritt: Koordinaten von  und
und  bestimmen
Die Koordinaten von
bestimmen
Die Koordinaten von  und
und  bestimmst du analog wie
bestimmst du analog wie  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{A‘}&=& \pmatrix{0 \\ 3\\ 3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d29818861f4f04018c40d97f85a9c80ba41ec3fcbb12aeeb304fa4689d906ed4?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{B‘}&=& \pmatrix{3 \\ 0\\ 3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/66fd66316409c332fba60940330f00134ad47b82ba1e7d4930ed7dc9034ce79b?color=5a5a5a) 2. Schritt: Streckenlängen bestimmen
Du bestimmst die Streckenlänge oder die Norm zwischen den Punkten mit dem Befehl norm:
2. Schritt: Streckenlängen bestimmen
Du bestimmst die Streckenlänge oder die Norm zwischen den Punkten mit dem Befehl norm:
 Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Alle vier Längen sind
Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Alle vier Längen sind  lang. Um zu zeigen, dass es sich um ein Quadrat handelt und nicht um ein Parallelogramm ist ein Rechterwinkel nachzuweisen.
3. Schritt: Rechtewinkel nachweisen
Für zwei rechtwinklige Vektoren gilt, dass das Skalarprodukt
lang. Um zu zeigen, dass es sich um ein Quadrat handelt und nicht um ein Parallelogramm ist ein Rechterwinkel nachzuweisen.
3. Schritt: Rechtewinkel nachweisen
Für zwei rechtwinklige Vektoren gilt, dass das Skalarprodukt  ist, du berechnest es mit dem Befehl Skalarprodukt:
ist, du berechnest es mit dem Befehl Skalarprodukt:
 und
und  , ausgehen von Punkt
, ausgehen von Punkt  .
.
 Abb. 3: Skalarprodukt berechnen
Ein Viereck mit vier gleich langen Seiten und einem rechten Winkel ist ein Quadrat, in diesem Fall mit der Seitenlänge
Abb. 3: Skalarprodukt berechnen
Ein Viereck mit vier gleich langen Seiten und einem rechten Winkel ist ein Quadrat, in diesem Fall mit der Seitenlänge  .
.
 Volumen berechnen
Du sollst das gegebene Volumen des Oktaeders nachweisen. Ein Oktaeder besteht aus zwei quadratischen Pyramiden, für deren Volumen
Volumen berechnen
Du sollst das gegebene Volumen des Oktaeders nachweisen. Ein Oktaeder besteht aus zwei quadratischen Pyramiden, für deren Volumen  gilt, wobei
gilt, wobei  den Flächeninhalt der Grundfläche und
den Flächeninhalt der Grundfläche und  die Höhe der Pyramide bezeichnet.
Die Höhe der Pyramide entspricht dem
die Höhe der Pyramide bezeichnet.
Die Höhe der Pyramide entspricht dem  -Abstand zwischen
-Abstand zwischen  und
und  bzw.
bzw.  oder der Hälfte des Abstandes zwischen
oder der Hälfte des Abstandes zwischen  und
und  .
.
![\(\begin{array}[t]{rll}
V&=& 2\cdot \frac{1}{3}\cdot \left(3\sqrt{2}\right)^2\cdot 3 \\[5pt]
&=& 2\cdot 18 \\[5pt]
&=& 36
\end{array}\)](https://mathjax.schullv.de/afb23bd42d701e30a121ef6fa120a419359596bec2639744c93beb69c177b58c?color=5a5a5a) Wie gefordert berträgt das Volumen der Pyramide
Wie gefordert berträgt das Volumen der Pyramide  .
.
 Winkel berechnen
Du sollst den Winkel zwischen den Seitenflächen
Winkel berechnen
Du sollst den Winkel zwischen den Seitenflächen  und
und  bestimmen.
bestimmen.
 Lösungsweg A: Mit dem Schnittwinkel zweier Geraden lösen
Den Schnittwinkel der beiden Seitenflächen kannst du auf die Schnittwinkel zweier Geraden bestimmen. Als Geraden wählst du die Verbindung zwischen
Lösungsweg A: Mit dem Schnittwinkel zweier Geraden lösen
Den Schnittwinkel der beiden Seitenflächen kannst du auf die Schnittwinkel zweier Geraden bestimmen. Als Geraden wählst du die Verbindung zwischen  bzw.
bzw.  und dem Mittelpunkt
und dem Mittelpunkt  der Strecke
der Strecke  und
und  .
1. Schritt: Mittelpunkt berechnen
Den Mittelpunkt erhältst du, wenn du zu
.
1. Schritt: Mittelpunkt berechnen
Den Mittelpunkt erhältst du, wenn du zu  die Hälfte der Strecke
die Hälfte der Strecke  addierst.
addierst.
![\(\begin{array}[t]{rll}
\overrightarrow{M}&=& \overrightarrow{A}+\frac{1}{2}\cdot\overrightarrow{AB} \\[5pt]
&=& \pmatrix{4,5 \\4,5 \\3 }
\end{array}\)](https://mathjax.schullv.de/3766e87b526dfff9dcccbf0739438ab52ba9d127c56b3e42213ac0ff0ce7cb1b?color=5a5a5a) Somit liegt der Mittelpunkt der Strecke bei
Somit liegt der Mittelpunkt der Strecke bei  .
2. Schritt: Vektoren
.
2. Schritt: Vektoren  und
und  bestimmen
Die Verbindungsvektoren
bestimmen
Die Verbindungsvektoren  und
und  bestimmst du wie zuvor
bestimmst du wie zuvor  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{MC}&=& \pmatrix{-1,5\\-1,5\\3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c5695eb10a8249ee7aeae64224eda3dda74505ab6f5d09b4aa5c7d736cdb3687?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{MC‘}&=& \pmatrix{-1,5\\-1,5\\-3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3e93e413c63345881d27a287111797fc8cbaa6667299738bd322fd2beae58d9c?color=5a5a5a) 3. Schritt: Schnittwinkel berechnen
Mit dem Winkelsatz kannst du aus diesen zwei Vektoren den Schnittwinkel bestimmen.
3. Schritt: Schnittwinkel berechnen
Mit dem Winkelsatz kannst du aus diesen zwei Vektoren den Schnittwinkel bestimmen.
 Für die Vektoren der Aufgabenstellung ergibt sich:
Für die Vektoren der Aufgabenstellung ergibt sich:
![\(\begin{array}[t]{rll}
\cos\varphi&=& -\frac{1}{3} &\quad \scriptsize \mid\; \arccos \\[5pt]
\varphi &=& \arccos \left(-\frac{1}{3}\right) \\[5pt]
&\approx & 109,47
\end{array}\)](https://mathjax.schullv.de/52658d7d91f48cd4baee6bcb6959345a903014bd5fd581ed47da8d57f8ae0f47?color=5a5a5a)
 Lösungsweg B: Mit dem Schnittwinkel zweier Ebenen lösen
Du kannst den Schnittwinkel über den Schnitt zweier Ebenen bestimmen. Dafür benötigst du allerdings die beiden Normalenvektoren. Dazu wählst du
Lösungsweg B: Mit dem Schnittwinkel zweier Ebenen lösen
Du kannst den Schnittwinkel über den Schnitt zweier Ebenen bestimmen. Dafür benötigst du allerdings die beiden Normalenvektoren. Dazu wählst du  bzw.
bzw.  als Stützvektor.
als Stützvektor.
![\(\begin{array}[t]{rll}
\vec n_1&=& \left( \overrightarrow{A}-\overrightarrow{C} \right)\times\left( \overrightarrow{B}-\overrightarrow{C} \right) \\[5pt]
&=& \pmatrix{9\\9\\9}
\end{array}\)](https://mathjax.schullv.de/c501561262115c3559b91c915354b9a19844e59049e3e7724c8b19f88760f167?color=5a5a5a)
![\(\begin{array}[t]{rll}
\vec n_2&=& \left( \overrightarrow{A}-\overrightarrow{C‘} \right)\times\left( \overrightarrow{B}-\overrightarrow{C‘} \right) \\[5pt]
&=& \pmatrix{-9\\-9\\9}
\end{array}\)](https://mathjax.schullv.de/65fe51549919fc266e033fe00b3c48c644a39ad8395bf17efcb7b40951a9d63b?color=5a5a5a) Mit dem Winkelsatz und diesen zwei Vektoren kannst du den Schnittwinkel der Ebene bestimmen.
Mit dem Winkelsatz und diesen zwei Vektoren kannst du den Schnittwinkel der Ebene bestimmen.
 Für die Vektoren der Aufgabenstellung ergibt sich:
Für die Vektoren der Aufgabenstellung ergibt sich:
![\(\begin{array}[t]{rll}
\cos\varphi&=& -\frac{1}{3} &\quad \scriptsize \mid\; \cos^{-1}s \\[5pt]
\varphi &=& \cos^{-1}\left(-\frac{1}{3}\right)\\[5pt]
&\approx & 109,47^{\circ}
\end{array}\)](https://mathjax.schullv.de/be3fc4eb81fb3b1009c9282e7ce87abd12f72555a7777b323891d0d97206f649?color=5a5a5a)
 Kugelgleichung angeben
Du sollst eine Gleichung für die Kugel angeben, auf welcher alle Eckpunkte des Oktaeders liegen. Der Mittelpunkt dieser Kugel liegt in
Kugelgleichung angeben
Du sollst eine Gleichung für die Kugel angeben, auf welcher alle Eckpunkte des Oktaeders liegen. Der Mittelpunkt dieser Kugel liegt in  , da die Punkte
, da die Punkte  ,
,  ,
,  und
und  alle den gleichen Abstand zu diesem haben. Der Radius ergibt sich somit aus der Länge des Vektors
alle den gleichen Abstand zu diesem haben. Der Radius ergibt sich somit aus der Länge des Vektors  .
.
![\(\begin{array}[t]{rll}
\vert \overrightarrow{AZ}\vert&=& \left|\pmatrix{3\\3\\3}-\pmatrix{6\\3\\3}\right| \\[5pt]
&=& 3
\end{array}\)](https://mathjax.schullv.de/c04b3cbbdff228230e970465ec9cb7b15f4bcb3c6ddf223a4667aecc2b84cd20?color=5a5a5a) Der Radius beträgt
Der Radius beträgt  somit ergibt sich die Kugelgleichung:
somit ergibt sich die Kugelgleichung:
![\(\begin{array}[t]{rll}
r^2&=& (x-3)^2+(y-3)^2+(z-3)^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6e7cc3ec5e13fd7ad4a561d9a6d7c968413b7e57ef5e01eb664ed894cc0ba4a7?color=5a5a5a) Dies Gleichung beschreibt die Kugel, auf welcher alle Eckpunkte und Spitzen des Oktaeders liegen.
Dies Gleichung beschreibt die Kugel, auf welcher alle Eckpunkte und Spitzen des Oktaeders liegen.
 Volumen der Kugel und des Oktaeders vergleichen
Du sollst die Volumina der Kugel und des Oktaeders vergleichen. Das Volumen des Oktaeders beträgt
Volumen der Kugel und des Oktaeders vergleichen
Du sollst die Volumina der Kugel und des Oktaeders vergleichen. Das Volumen des Oktaeders beträgt  . Für das Kugelvolumen gilt:
. Für das Kugelvolumen gilt:
 Für
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
V&=& \frac{4}{3}\cdot\pi\cdot 3^3\\[5pt]
&=& 36\pi
\end{array}\)](https://mathjax.schullv.de/975e5046a4aa4b21ef82cad1238cbddb3e80e10968d4a422a0fdc8bc4ddae02d?color=5a5a5a) Das Volumen der Kugel ist etwas mehr als dreimal so groß wie das des Oktaeders. Oder anders: Der Oktaeder nimmt
Das Volumen der Kugel ist etwas mehr als dreimal so groß wie das des Oktaeders. Oder anders: Der Oktaeder nimmt  des Kugelvolumens ein.
Aufgabengruppe 2
des Kugelvolumens ein.
Aufgabengruppe 2
 Benötigte Seillänge berechnen
Du sollst die benötigte Seillänge an den vier Masten zum Ablassen der Kamera berechnen. Betrachte hierzu den Längenunterschied der Strecken
Benötigte Seillänge berechnen
Du sollst die benötigte Seillänge an den vier Masten zum Ablassen der Kamera berechnen. Betrachte hierzu den Längenunterschied der Strecken  und
und  .
Die benötigten Koordinaten von
.
Die benötigten Koordinaten von  und
und  erhältst du aus der Aufgabenstellung.
erhältst du aus der Aufgabenstellung.
![\(\begin{array}[t]{rll}
\overrightarrow{K_0}&=& \overrightarrow{A}+25\cdot e_3 \\[5pt]
&=& \pmatrix{45\\60\\25}
\end{array}\)](https://mathjax.schullv.de/0f25b61bc4991c1cc9d2b7a3d6ba42fa9406dcf36468897beb7c3deff6de10d1?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{K_1}&=& \overrightarrow{K_0}-19\cdot e_3 \\[5pt]
&=&\pmatrix{45\\60\\6}
\end{array}\)](https://mathjax.schullv.de/7d2a01fb88fb38553d85902926e00615b8eaa727d979934729445bcd45c0794b?color=5a5a5a) Die Länge ergibt sich aus dem Betrag bzw. der Norm, deren Befehl findest du unter:
Die Länge ergibt sich aus dem Betrag bzw. der Norm, deren Befehl findest du unter:
 :
:
 Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
Die benötigte Seillänge
Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
Die benötigte Seillänge  pro Mast ergibt sich aus der Differenz dieser beiden Abstände:
pro Mast ergibt sich aus der Differenz dieser beiden Abstände:
![\(\begin{array}[t]{rll}
l&=& 3\cdot \sqrt{689} - 5\cdot \sqrt{689} \\[5pt]
&\approx & 3,58
\end{array}\)](https://mathjax.schullv.de/5365510f091749218811cd9507167b2ff7041349f5aab9de388f42e004a67afe?color=5a5a5a) Pro Mast werden
Pro Mast werden  m Seillänge benötigt.
m Seillänge benötigt.
 Winkel gegen die Horizontale berechnen
Du sollst den Winkel des Seils, welches durch
Winkel gegen die Horizontale berechnen
Du sollst den Winkel des Seils, welches durch  beschrieben wird, zur Horizontalen berechnen. Die Horizontale entspricht einer
beschrieben wird, zur Horizontalen berechnen. Die Horizontale entspricht einer  -Koordinate von
-Koordinate von  .
.
![\(\begin{array}[t]{rll}
\cos\varphi&=& \frac{\pmatrix{45\\60\\-24}\cdot \pmatrix{45\\60\\0}}{\left|\pmatrix{45\\60\\0}\right|\cdot\left|\pmatrix{45\\60\\-24}\right|} \\[5pt]
\varphi&\approx& 17,74^\circ
\end{array}\)](https://mathjax.schullv.de/e5c3d85e581665b20fb0f0202c42bdcd08b70e0fe9b5d4d8d09851e368abfa17?color=5a5a5a) Das Seil und die Horizontale schließen einen Winkel von
Das Seil und die Horizontale schließen einen Winkel von  ein.
ein.
 Koordinaten von
Koordinaten von  ermitteln
Du sollst die Koordinaten von
ermitteln
Du sollst die Koordinaten von  bestimmen.
bestimmen.  liegt auf der Geraden
liegt auf der Geraden  mit
mit  . Desweiteren ist bekannt, dass die
. Desweiteren ist bekannt, dass die  Koordinate von
Koordinate von 
 ist. Du erhältst drei Gleichungen aus den drei Komponenten, du löst sie mit:
ist. Du erhältst drei Gleichungen aus den drei Komponenten, du löst sie mit:
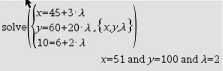 Abb. 5: Lineares Gleichungssystem lösen
Die Koordinaten von
Abb. 5: Lineares Gleichungssystem lösen
Die Koordinaten von  sind
sind  .
.
 Drehwinkel zum Ball berechnen
Du sollst berechnen, um welchen Drehwinkel die Kamera gedreht werden muss, damit sie den Ball auf
Drehwinkel zum Ball berechnen
Du sollst berechnen, um welchen Drehwinkel die Kamera gedreht werden muss, damit sie den Ball auf  anvisiert.
Betrachte dieses Problem zwei dimensional.
Der Abstand in
anvisiert.
Betrachte dieses Problem zwei dimensional.
Der Abstand in  -Richutng beträgt
-Richutng beträgt  , der Abstand in
, der Abstand in  -Richtung beträgt
-Richtung beträgt  . Zusammen beträgt der Abstand
. Zusammen beträgt der Abstand  in der
in der  -Ebene:
-Ebene:
![\(\begin{array}[t]{rll}
d&=& \sqrt{11^2+5^2} \\[5pt]
&=& \sqrt{146} \\[5pt]
&\approx & 12,08
\end{array}\)](https://mathjax.schullv.de/4ef857f11270e586ccd3ae55555d17a66a2448f000c6bd2b5de392a6e5f2874b?color=5a5a5a) Auf
Auf  m ist ein Höhenunterschied von
m ist ein Höhenunterschied von  m zu überwinden. Mit der Trigonometrie ergibt sich:
m zu überwinden. Mit der Trigonometrie ergibt sich:
![\(\begin{array}[t]{rll}
\tan\varphi&=& \frac{d}{h} &\quad \scriptsize \mid\; \arctan\\[5pt]
\varphi&=& \arctan\left(\frac{12,08}{10}\right) \\[5pt]
&\approx & 50,38^\circ
\end{array}\)](https://mathjax.schullv.de/47e64eeea1f36fb4354c5366994c9e2893604144f07b6a588f6bd9cc51c26bcd?color=5a5a5a) Es ist eine Drehung um
Es ist eine Drehung um  notwendig.
notwendig.
 Ebenengleichung ermitteln
Du sollst eine Ebenengleichung für die Ebene durch die drei Punkte
Ebenengleichung ermitteln
Du sollst eine Ebenengleichung für die Ebene durch die drei Punkte  ,
,  und
und  ermitteln. Wähle
ermitteln. Wähle  als Stützpunkt. Für die Koordinatenform benötigst du den Normalenvektor, welchen du aus dem Kreuzprodukt der beiden Spannvektoren
als Stützpunkt. Für die Koordinatenform benötigst du den Normalenvektor, welchen du aus dem Kreuzprodukt der beiden Spannvektoren  und
und  erhältst. Den notwendigen Befehl findest du unter:
erhältst. Den notwendigen Befehl findest du unter:
 Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
Für die Normalenform einer Ebene kannst du ein Vielfaches des Normalenvektors verwenden. Du teilst somit jede Komponente des errechneten Vektors durch
Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
Für die Normalenform einer Ebene kannst du ein Vielfaches des Normalenvektors verwenden. Du teilst somit jede Komponente des errechneten Vektors durch  . Die Ebene ist somit von folgender Form:
. Die Ebene ist somit von folgender Form:
![\(\begin{array}[t]{rll}
d&=& 1\cdot x_2+5\cdot x_3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f52acc2de0bfdeea034bd9898e9ac5400f12d1ab497f290320cdfeef8347839a?color=5a5a5a) Um die Konstante
Um die Konstante  zu ermitteln, setzt du den Stützpunkt
zu ermitteln, setzt du den Stützpunkt  ein.
ein.
![\(\begin{array}[t]{rll}
d&=& 5\cdot 30 \\[5pt]
&=& 150
\end{array}\)](https://mathjax.schullv.de/1b7e5f42c3e7e19112249d09b38e9cc19392f385e937976f88573e754325c8ea?color=5a5a5a) Die Gleichung mit
Die Gleichung mit  bschriebt die Ebene durch die geforderten Punkte.
bschriebt die Ebene durch die geforderten Punkte.

 liegt unterhalb der Ebene nachweisen
Du sollst nachweisen, dass
liegt unterhalb der Ebene nachweisen
Du sollst nachweisen, dass  unterhalb der Ebene liegt. Dazu setzt du die
unterhalb der Ebene liegt. Dazu setzt du die  - und
- und  -Koordinaten in die Ebenengleichung ein und berechnest
-Koordinaten in die Ebenengleichung ein und berechnest  .
.
![\(\begin{array}[t]{rll}
150 &=& 70+5\cdot x_3 &\quad \scriptsize \mid\; -70 \\[5pt]
80&=& 5\cdot x_3 &\quad \scriptsize \mid\; :5 \\[5pt]
x_3&=& 16
\end{array}\)](https://mathjax.schullv.de/1d22287444c8023ac952b6a6bc1d5133dfd6a51ce0c9834bb6cf1c1c69ba06e2?color=5a5a5a) Die
Die  -Koordinate des Punktes in der Ebene mit
-Koordinate des Punktes in der Ebene mit  und
und  beträgt
beträgt  . Die
. Die  -Koordinate von
-Koordinate von  beträgt allerdings nur
beträgt allerdings nur  , somit liegt
, somit liegt  unterhalb der Ebene.
unterhalb der Ebene.
 Schlussfolgerung falsifizieren
Du sollst plausible machen, dass im Allgemeinen die Aussage falsch ist, dass wenn der höchste Punkt der Flugbahn eines Balles unterhalb von
Schlussfolgerung falsifizieren
Du sollst plausible machen, dass im Allgemeinen die Aussage falsch ist, dass wenn der höchste Punkt der Flugbahn eines Balles unterhalb von  liegt er die Seile nicht berühren kann. Dazu betrachtest du eine Schuss welcher bei
liegt er die Seile nicht berühren kann. Dazu betrachtest du eine Schuss welcher bei  in Richtung
in Richtung  abgestoßen wird.
Sein höchster Punkt liegt beispielsweise bei
abgestoßen wird.
Sein höchster Punkt liegt beispielsweise bei  und somit unterhalb der Eben, aber durch seine Parabel-Flugbahn landet er gleich daraufhin im Seil.
Bildnachweise [nach oben]
und somit unterhalb der Eben, aber durch seine Parabel-Flugbahn landet er gleich daraufhin im Seil.
Bildnachweise [nach oben]
a)
Menu  Matrix und Vektor
Matrix und Vektor  Vektor
Vektor  Kreuzprodukt
Kreuzprodukt
 Abb. 1: Kreuzprodukt mit dem nspire berechnen
Abb. 1: Kreuzprodukt mit dem nspire berechnen
b)
c)
Menu  Matrix und Vektor
Matrix und Vektor  Normen
Normen  Norm
Norm
Die Vektoren zwischen den Punkten ermittelst du wie zuvor.
 Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Menu  Matrix und Vektor
Matrix und Vektor  Vektor
Vektor  Skalarprodukt
Skalarprodukt
Betrachte die Vektoren  Abb. 3: Skalarprodukt berechnen
Abb. 3: Skalarprodukt berechnen
d)
e)
f)
g)
a)
menu  Matrix und Vektor
Matrix und Vektor  Normen
Normen  Norm
Norm
Für die Vektoren ergibt sich der Abstand zu  Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
b)
c)
menu  Algebra
Algebra  Gleichungssystem lösen
Gleichungssystem lösen  Gleichungssystem lösen
Gleichungssystem lösen
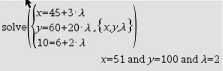 Abb. 5: Lineares Gleichungssystem lösen
Abb. 5: Lineares Gleichungssystem lösen
d)
e)
menu  Matrix und Vektor
Matrix und Vektor  Vaktor
Vaktor  Kreuzprodukt
Kreuzprodukt
 Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
f)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabengruppe 1
 Normalenform aufstellen
Du sollst die Normalenform der Ebene
Normalenform aufstellen
Du sollst die Normalenform der Ebene  durch die drei Punkte
durch die drei Punkte  ,
,  ,
,  bestimmen. Die Normalenform erhältst du durch
bestimmen. Die Normalenform erhältst du durch
 Dabei bezeichnet
Dabei bezeichnet  den Stützvektor und
den Stützvektor und  den Normalenvektor, welcher senkrecht auf den zwei Spannvektoren steht.
Benutze
den Normalenvektor, welcher senkrecht auf den zwei Spannvektoren steht.
Benutze  als Ausgangspunkt der Ebene und als Spannvektoren
als Ausgangspunkt der Ebene und als Spannvektoren  und
und  .
1. Schritt: Spannvektoren berechnen
Die Spannvektoren entsprechen dem Vektor zwischen
.
1. Schritt: Spannvektoren berechnen
Die Spannvektoren entsprechen dem Vektor zwischen  und
und  bzw.
bzw.  und
und  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=& \vec B-\vec A \\[5pt]
&=&\pmatrix{3 \\ 6 \\ 3}-\pmatrix{6 \\ 3 \\ 3} \\[5pt]
&=&\pmatrix{-3\\3\\0}
\end{array}\)](https://mathjax.schullv.de/7af650ed19f75e4c11011791fd5b3c5a08f299062b96c3741ad985b855d6b0bb?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{AC}&=& \vec C-\vec A \\[5pt]
&=&\pmatrix{3 \\ 3 \\ 6}-\pmatrix{6 \\ 3 \\ 3} \\[5pt]
&=&\pmatrix{-3\\0\\3}
\end{array}\)](https://mathjax.schullv.de/c86e30403a16954aaa217f8b7c2f997e4072d07005fa8ff7ee16fbc6aab1c77c?color=5a5a5a) 2. Schritt: Normalenvektor berechnen
Mit dem Kreuzprodukt kannst du den Normalenvektor bestimmen, dazu verwendest du den Befehl crossP, du findest ihn unter:
2. Schritt: Normalenvektor berechnen
Mit dem Kreuzprodukt kannst du den Normalenvektor bestimmen, dazu verwendest du den Befehl crossP, du findest ihn unter:
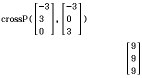 Abb. 1: Kreuzprodukt mit dem Classpad berechnen
Du erhältst das Kreuzprodukt
Abb. 1: Kreuzprodukt mit dem Classpad berechnen
Du erhältst das Kreuzprodukt  . Für eine Ebene kannst du auch ein Vielfaches des Normalenvektors verwenden. Dies ermöglicht es dir Ebenengleichungen zu vereinfachen. Für die Normalenform erhältst du:
. Für eine Ebene kannst du auch ein Vielfaches des Normalenvektors verwenden. Dies ermöglicht es dir Ebenengleichungen zu vereinfachen. Für die Normalenform erhältst du:
![\(\begin{array}[t]{rll}
E : & 1\cdot x_1+1\cdot x_2+1\cdot x_3=d & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/ecd5fb128303ca9a27f967c140ff05120a4e220d53353ea8da4f19938c645d9e?color=5a5a5a) Die Konstante
Die Konstante  bestimmst du durch Einsetzen eines Punktes, welcher sicher in der Ebene liegt. Dazu verwendest du den Stützpunkt
bestimmst du durch Einsetzen eines Punktes, welcher sicher in der Ebene liegt. Dazu verwendest du den Stützpunkt  .
.
![\(\begin{array}[t]{rll}
d&=& 6+3+3 \\[5pt]
&=& 12
\end{array}\)](https://mathjax.schullv.de/b4afb1be8b6cec976f3bf3a01d752685e6476c547b95e8ee663a1a4627852e63?color=5a5a5a) Du erhältst die Normalenform der Ebene mit:
Du erhältst die Normalenform der Ebene mit:
![\(\begin{array}[t]{rll}
E : & 1\cdot x_1+1\cdot x_2+1\cdot x_3=12 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d34e381e24aa65cb5b5c1508ec059649f53efb4b498310c37964e7ad7f1a5212?color=5a5a5a)
 Lage der Ebene beschreiben
Du sollst die Lage der Ebene durch die drei Punkte
Lage der Ebene beschreiben
Du sollst die Lage der Ebene durch die drei Punkte  ,
,  und
und  beschreiben. Aller drei Punkte besitzen die gleiche
beschreiben. Aller drei Punkte besitzen die gleiche  -Koordinate.
Somit liegen die Punkte in einer mit dem Abstand
-Koordinate.
Somit liegen die Punkte in einer mit dem Abstand  zur
zur  -Ebene parallelen Ebene.
-Ebene parallelen Ebene.

 senkrecht zur Ebene nachweisen
Du sollst nachweisen, dass die Strecke bzw. der Vektor
senkrecht zur Ebene nachweisen
Du sollst nachweisen, dass die Strecke bzw. der Vektor  senkrecht zur Ebene ist. Dazu bestimmst du zuerst die Koordinaten von
senkrecht zur Ebene ist. Dazu bestimmst du zuerst die Koordinaten von  .
1. Schritt: Koordinaten von
.
1. Schritt: Koordinaten von  bestimmen
bestimmen
 entsteht durch Spiegelung von
entsteht durch Spiegelung von  an
an  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{C‘}&=& 2\cdot \overrightarrow{CZ}+\overrightarrow{C} \\[5pt]
&=& 2\cdot \left( \overrightarrow{Z}-\overrightarrow{C} \right)+\overrightarrow{C} \\[5pt]
&=& 2\cdot \left( \pmatrix{3\\3\\3}-\pmatrix{3\\3\\6}\right)+\pmatrix{3\\3\\6} \\[5pt]
&=& 2\cdot \pmatrix{0\\0\\-3}+\pmatrix{3\\3\\6} \\[5pt]
&=& \pmatrix{3\\3\\0}
\end{array}\)](https://mathjax.schullv.de/f4cb9c01eaa6013f82def2626fa97ab945d84599f0a23256497f99b39c5aef01?color=5a5a5a) 2. Schritt:
2. Schritt:  bestimmen
Desweiteren wird der Vektor
bestimmen
Desweiteren wird der Vektor  benötigt.
benötigt.
![\(\begin{array}[t]{rll}
\overrightarrow{CC‘}&=& \overrightarrow{C‘}-\overrightarrow{C} \\[5pt]
&=& \pmatrix{3\\3\\0}-\pmatrix{3\\3\\6} \\[5pt]
&=& \pmatrix{0\\0\\-6}
\end{array}\)](https://mathjax.schullv.de/0c9fce91f5701aaeace336988503b5ed7ded42c184094306fa65eab0fa0d556f?color=5a5a5a) 3. Schritt: Senkrecht nachweisen
Vektoren welche senkrecht zu einer Ebene stehen sind Vielfache des Normalenvektors. Da die Ebene parallel zur
3. Schritt: Senkrecht nachweisen
Vektoren welche senkrecht zu einer Ebene stehen sind Vielfache des Normalenvektors. Da die Ebene parallel zur  -Ebene ist, ist ihr Normalenvektor
-Ebene ist, ist ihr Normalenvektor  . Es muss somit ein
. Es muss somit ein  geben, dass gilt:
geben, dass gilt:
![\(\begin{array}[t]{rll}
\pmatrix{0\\0\\-6}&=& \lambda\cdot \pmatrix{0\\0\\1} \\[5pt]
\lambda&=& -6
\end{array}\)](https://mathjax.schullv.de/e965baf9de8fd30279c1e4333e7685ef9639f837b9be87ae57d47145ce942e9e?color=5a5a5a) Da ein
Da ein  existiert, steht
existiert, steht  senkrecht auf der Ebene.
senkrecht auf der Ebene.
 Seitenlänge des Quadrats begründen
Du sollst begründen, dass es sich bei dem Viereck
Seitenlänge des Quadrats begründen
Du sollst begründen, dass es sich bei dem Viereck  um ein Quadrat mit Seitenlänge
um ein Quadrat mit Seitenlänge  handelt. Bestimme zuerst die Koordinaten von
handelt. Bestimme zuerst die Koordinaten von  und
und  .
1. Schritt: Koordinaten von
.
1. Schritt: Koordinaten von  und
und  bestimmen
Die Koordinaten von
bestimmen
Die Koordinaten von  und
und  bestimmst du analog wie
bestimmst du analog wie  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{A‘}&=& \pmatrix{0 \\ 3\\ 3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d29818861f4f04018c40d97f85a9c80ba41ec3fcbb12aeeb304fa4689d906ed4?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{B‘}&=& \pmatrix{3 \\ 0\\ 3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/66fd66316409c332fba60940330f00134ad47b82ba1e7d4930ed7dc9034ce79b?color=5a5a5a) 2. Schritt: Streckenlängen bestimmen
Du bestimmst die Streckenlänge oder die Norm zwischen den Punkten mit dem Befehl norm:
2. Schritt: Streckenlängen bestimmen
Du bestimmst die Streckenlänge oder die Norm zwischen den Punkten mit dem Befehl norm:
 Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Alle vier Längen sind
Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Alle vier Längen sind  lang. Um zu zeigen, dass es sich um ein Quadrat handelt und nicht um ein Parallelogramm ist ein Rechterwinkel nachzuweisen.
3. Schritt: Rechtewinkel nachweisen
Für zwei rechtwinklige Vektoren gilt, dass das Skalarprodukt
lang. Um zu zeigen, dass es sich um ein Quadrat handelt und nicht um ein Parallelogramm ist ein Rechterwinkel nachzuweisen.
3. Schritt: Rechtewinkel nachweisen
Für zwei rechtwinklige Vektoren gilt, dass das Skalarprodukt  ist, du berechnest es mit dem Befehl dotP:
ist, du berechnest es mit dem Befehl dotP:
 und
und  , ausgehen von Punkt
, ausgehen von Punkt  .
.
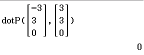 Abb. 3: Skalarprodukt berechnen
Ein Viereck mit vier gleich langen Seiten und einem rechten Winkel ist ein Quadrat, in diesem Fall mit der Seitenlänge
Abb. 3: Skalarprodukt berechnen
Ein Viereck mit vier gleich langen Seiten und einem rechten Winkel ist ein Quadrat, in diesem Fall mit der Seitenlänge  .
.
 Volumen berechnen
Du sollst das gegebene Volumen des Oktaeders nachweisen. Ein Oktaeder besteht aus zwei quadratischen Pyramiden, für deren Volumen
Volumen berechnen
Du sollst das gegebene Volumen des Oktaeders nachweisen. Ein Oktaeder besteht aus zwei quadratischen Pyramiden, für deren Volumen  gilt, wobei
gilt, wobei  den Flächeninhalt der Grundfläche und
den Flächeninhalt der Grundfläche und  die Höhe der Pyramide bezeichnet.
Die Höhe der Pyramied entspricht dem
die Höhe der Pyramide bezeichnet.
Die Höhe der Pyramied entspricht dem  -Abstand zwischen
-Abstand zwischen  und
und  bzw.
bzw.  oder der Hälfte des Abstandes zwischen
oder der Hälfte des Abstandes zwischen  und
und  .
.
![\(\begin{array}[t]{rll}
V&=& 2\cdot \frac{1}{3}\cdot \left(3\sqrt{2}\right)^2\cdot 3 \\[5pt]
&=& 2\cdot 18 \\[5pt]
&=& 36
\end{array}\)](https://mathjax.schullv.de/eda2cc170059b35a2c57ba0b836ab3c5a36b866e67ab51dd9311952bdb34f7eb?color=5a5a5a) Wie gefordert berträgt das Volumen der Pyramide
Wie gefordert berträgt das Volumen der Pyramide  .
.
 Winkel berechnen
Du sollst den Winkel zwischen den Seitenflächen
Winkel berechnen
Du sollst den Winkel zwischen den Seitenflächen  und
und  bestimmen.
bestimmen.
 Lösungsweg A: Mit dem Schnittwinkel zweier Geraden lösen
Den Schnittwinkel der beiden Seitenflächen kannst du auf die Schnittwinkel zweier Geraden bestimmen. Als Geraden wählst du die Verbindung zwischen
Lösungsweg A: Mit dem Schnittwinkel zweier Geraden lösen
Den Schnittwinkel der beiden Seitenflächen kannst du auf die Schnittwinkel zweier Geraden bestimmen. Als Geraden wählst du die Verbindung zwischen  bzw.
bzw.  und dem Mittelpunkt
und dem Mittelpunkt  der Strecke
der Strecke  und
und  .
1. Schritt: Mittelpunkt berechnen
Den Mittelpunkt erhältst du, wenn du zu
.
1. Schritt: Mittelpunkt berechnen
Den Mittelpunkt erhältst du, wenn du zu  die Hälfte der Strecke
die Hälfte der Strecke  addierst.
addierst.
![\(\begin{array}[t]{rll}
\overrightarrow{M}&=& \overrightarrow{A}+\frac{1}{2}\cdot\overrightarrow{AB} \\[5pt]
&=& \pmatrix{4,5 \\4,5 \\3 }
\end{array}\)](https://mathjax.schullv.de/3766e87b526dfff9dcccbf0739438ab52ba9d127c56b3e42213ac0ff0ce7cb1b?color=5a5a5a) Somit liegt der Mittelpunkt der Strecke bei
Somit liegt der Mittelpunkt der Strecke bei  .
2. Schritt: Vektoren
.
2. Schritt: Vektoren  und
und  bestimmen
Die Verbindungsvektoren
bestimmen
Die Verbindungsvektoren  und
und  bestimmst du wie zuvor
bestimmst du wie zuvor  .
.
![\(\begin{array}[t]{rll}
\overrightarrow{MC}&=& \pmatrix{-1,5\\-1,5\\3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c5695eb10a8249ee7aeae64224eda3dda74505ab6f5d09b4aa5c7d736cdb3687?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{MC‘}&=& \pmatrix{-1,5\\-1,5\\-3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3e93e413c63345881d27a287111797fc8cbaa6667299738bd322fd2beae58d9c?color=5a5a5a) 3. Schritt: Schnittwinkel berechnen
Mit dem Winkelsatz kannst du aus diesen zwei Vektoren den Schnittwinkel bestimmen.
3. Schritt: Schnittwinkel berechnen
Mit dem Winkelsatz kannst du aus diesen zwei Vektoren den Schnittwinkel bestimmen.
 Für die Vektoren der Aufgabenstellung ergibt sich:
Für die Vektoren der Aufgabenstellung ergibt sich:
![\(\begin{array}[t]{rll}
\cos\varphi&=& -\frac{1}{3} &\quad \scriptsize \mid\; \arccos \\[5pt]
\varphi &=& \arccos \left(-\frac{1}{3}\right) \\[5pt]
&\approx & 109,47^{\circ}
\end{array}\)](https://mathjax.schullv.de/e09edacaed12963d4b60c92c18cffcaddf22e959b0a68a99ba888a11c6f5b558?color=5a5a5a)
 Lösungsweg B: Mit dem Schnittwinkel zweier Ebenen lösen
Du kannst den Schnittwinkel über den Schnitt zweier Ebenen bestimmen. Dafür benötigst du allerdings die beiden Normalenvektoren. Dazu wählst du
Lösungsweg B: Mit dem Schnittwinkel zweier Ebenen lösen
Du kannst den Schnittwinkel über den Schnitt zweier Ebenen bestimmen. Dafür benötigst du allerdings die beiden Normalenvektoren. Dazu wählst du  bzw.
bzw.  als Stützvektor.
als Stützvektor.
![\(\begin{array}[t]{rll}
\vec n_1&=& \left( \overrightarrow{A}-\overrightarrow{C} \right)\times\left( \overrightarrow{B}-\overrightarrow{C} \right) \\[5pt]
&=& \pmatrix{9\\9\\9}
\end{array}\)](https://mathjax.schullv.de/c501561262115c3559b91c915354b9a19844e59049e3e7724c8b19f88760f167?color=5a5a5a)
![\(\begin{array}[t]{rll}
\vec n_2&=& \left( \overrightarrow{A}-\overrightarrow{C‘} \right)\times\left( \overrightarrow{B}-\overrightarrow{C‘} \right) \\[5pt]
&=& \pmatrix{-9\\-9\\9}
\end{array}\)](https://mathjax.schullv.de/65fe51549919fc266e033fe00b3c48c644a39ad8395bf17efcb7b40951a9d63b?color=5a5a5a) Mit dem Winkelsatz und diesen zwei Vektoren kannst du den Schnittwinkel der Ebene bestimmen.
Mit dem Winkelsatz und diesen zwei Vektoren kannst du den Schnittwinkel der Ebene bestimmen.
 Für die Vektoren der Aufgabenstellung ergibt sich:
Für die Vektoren der Aufgabenstellung ergibt sich:
![\(\begin{array}[t]{rll}
\cos\varphi&=& -\frac{1}{3} &\quad \scriptsize \mid\; \arccos \\[5pt]
\varphi &=& \arccos \left(-\frac{1}{3}\right)\\[5pt]
&\approx & 109,47^{\circ}
\end{array}\)](https://mathjax.schullv.de/1c9eb3cf4c71442ad1f6d9d6f581b55e9ea46610b3a43445c8ac90df80f4fd8a?color=5a5a5a)
 Kugelgleichung angeben
Du sollst eine Gleichung für die Kugel angeben, auf welcher alle Eckpunkte des Oktaeders liegen. Der Mittelpunkt dieser Kugel liegt in
Kugelgleichung angeben
Du sollst eine Gleichung für die Kugel angeben, auf welcher alle Eckpunkte des Oktaeders liegen. Der Mittelpunkt dieser Kugel liegt in  , da die Punkte
, da die Punkte  ,
,  ,
,  und
und  alle den gleichen Abstand zu diesem haben. Der Radius ergibt sich somit aus der Länge des Vektors
alle den gleichen Abstand zu diesem haben. Der Radius ergibt sich somit aus der Länge des Vektors  .
.
![\(\begin{array}[t]{rll}
\vert \overrightarrow{AZ}\vert&=& \left|\pmatrix{3\\3\\3}-\pmatrix{6\\3\\3}\right| \\[5pt]
&=& 3
\end{array}\)](https://mathjax.schullv.de/c04b3cbbdff228230e970465ec9cb7b15f4bcb3c6ddf223a4667aecc2b84cd20?color=5a5a5a) Der Radius beträgt
Der Radius beträgt  somit ergibt sich die Kugelgleichung:
somit ergibt sich die Kugelgleichung:
![\(\begin{array}[t]{rll}
r^2&=& (x-3)^2+(y-3)^2+(z-3)^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c7b7550086a36b81805066bd48bda95f88876c712993df8a1b7fa0f5130ff32a?color=5a5a5a) Dies Gleichung beschreibt die Kugel, auf welcher alle Eckpunkte und Spitzen des Oktaeders liegen.
Dies Gleichung beschreibt die Kugel, auf welcher alle Eckpunkte und Spitzen des Oktaeders liegen.
 Volumen der Kugel und des Oktaeders vergleichen
Du sollst die Volumina der Kugel und des Oktaeders vergleichen. Das Volumen des Oktaeders beträgt
Volumen der Kugel und des Oktaeders vergleichen
Du sollst die Volumina der Kugel und des Oktaeders vergleichen. Das Volumen des Oktaeders beträgt  . Für das Kugelvolumen gilt:
. Für das Kugelvolumen gilt:
 Für
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
V&=& \frac{4}{3}\cdot\pi\cdot 3^3 \\[5pt]
&=& 36\pi
\end{array}\)](https://mathjax.schullv.de/d309380d0595e56599f07c4f578927d2db2ae0097c391447673c83c2c6ba2982?color=5a5a5a) Das Volumen der Kugel ist etwas mehr als dreimal so groß wie das des Oktaeders. Oder anders: Der Oktaeder nimmt
Das Volumen der Kugel ist etwas mehr als dreimal so groß wie das des Oktaeders. Oder anders: Der Oktaeder nimmt  des Kugelvolumens ein.
Aufgabengruppe 2
des Kugelvolumens ein.
Aufgabengruppe 2
 Benötigte Seillänge berechnen
Du sollst die benötigte Seillänge an den vier Masten zum Ablassen der Kamera berechnen. Betrachte hierzu den Längenunterschied der Strecken
Benötigte Seillänge berechnen
Du sollst die benötigte Seillänge an den vier Masten zum Ablassen der Kamera berechnen. Betrachte hierzu den Längenunterschied der Strecken  und
und  .
Die benötigten Koordinaten von
.
Die benötigten Koordinaten von  und
und  erhältst du aus der Aufgabenstellung.
erhältst du aus der Aufgabenstellung.
![\(\begin{array}[t]{rll}
\overrightarrow{K_0}&=& \overrightarrow{A}+25\cdot e_3 \\[5pt]
&=& \pmatrix{45\\60\\25}
\end{array}\)](https://mathjax.schullv.de/0f25b61bc4991c1cc9d2b7a3d6ba42fa9406dcf36468897beb7c3deff6de10d1?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{K_1}&=& \overrightarrow{K_0}-19\cdot e_3 \\[5pt]
&=&\pmatrix{45\\60\\6}
\end{array}\)](https://mathjax.schullv.de/7d2a01fb88fb38553d85902926e00615b8eaa727d979934729445bcd45c0794b?color=5a5a5a) Die Länge ergibt sich aus dem Betrag bzw. der Norm, deren Befehl findest du unter:
Die Länge ergibt sich aus dem Betrag bzw. der Norm, deren Befehl findest du unter:
 :
:
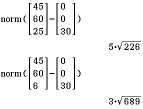 Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
Die benötigte Seillänge
Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
Die benötigte Seillänge  pro Mast ergibt sich aus der Differenz dieser beiden Abstände:
pro Mast ergibt sich aus der Differenz dieser beiden Abstände:
![\(\begin{array}[t]{rll}
l&=& 3\cdot \sqrt{689} - 5\cdot \sqrt{689} \\[5pt]
&\approx & 3,58
\end{array}\)](https://mathjax.schullv.de/5365510f091749218811cd9507167b2ff7041349f5aab9de388f42e004a67afe?color=5a5a5a) Pro Mast werden
Pro Mast werden  m Seillänge benötigt.
m Seillänge benötigt.
 Winkel gegen die Horizontale berechnen
Du sollst den Winkel des Seils, welches durch
Winkel gegen die Horizontale berechnen
Du sollst den Winkel des Seils, welches durch  beschrieben wird, zur Horizontalen berechnen. Die Horizontale entspricht einer
beschrieben wird, zur Horizontalen berechnen. Die Horizontale entspricht einer  -Koordinate von
-Koordinate von  .
.
![\(\begin{array}[t]{rll}
\cos\varphi&=& \frac{\pmatrix{45\\60\\-24}\cdot \pmatrix{45\\60\\0}}{\left|\pmatrix{45\\60\\0}\right|\cdot\left|\pmatrix{45\\60\\-24}\right|} \\[5pt]
\varphi&\approx& 17,74^\circ
\end{array}\)](https://mathjax.schullv.de/e5c3d85e581665b20fb0f0202c42bdcd08b70e0fe9b5d4d8d09851e368abfa17?color=5a5a5a) Das Seil und die Horizontale schließen einen Winkel von
Das Seil und die Horizontale schließen einen Winkel von  ein.
ein.
 Koordinaten von
Koordinaten von  ermitteln
Du sollst die Koordinaten von
ermitteln
Du sollst die Koordinaten von  bestimmen.
bestimmen.  liegt auf der Geraden
liegt auf der Geraden  mit
mit  . Desweiteren ist bekannt, dass die
. Desweiteren ist bekannt, dass die  Koordinate von
Koordinate von 
 ist. Du erhältst drei Gleichungen aus den drei Komponenten, du löst sie mit:
ist. Du erhältst drei Gleichungen aus den drei Komponenten, du löst sie mit:
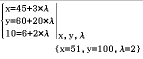 Abb. 5: Lineares Gleichungssystem lösen
Die Koordinaten von
Abb. 5: Lineares Gleichungssystem lösen
Die Koordinaten von  sind
sind  .
.
 Drehwinkel zum Ball berechnen
Du sollst berechnen, um welchen Drehwinkel die Kamera gedreht werden muss, damit sie den Ball auf
Drehwinkel zum Ball berechnen
Du sollst berechnen, um welchen Drehwinkel die Kamera gedreht werden muss, damit sie den Ball auf  anvisiert.
Betrachte dieses Problem zwei dimensional.
Der Abstand in
anvisiert.
Betrachte dieses Problem zwei dimensional.
Der Abstand in  -Richutng beträgt
-Richutng beträgt  , der Abstand in
, der Abstand in  -Richtung beträgt
-Richtung beträgt  . Zusammen beträgt der Abstand
. Zusammen beträgt der Abstand  in der
in der  -Ebene:
-Ebene:
![\(\begin{array}[t]{rll}
d&=& \sqrt{11^2+5^2} \\[5pt]
&=& \sqrt{146} \\[5pt]
&\approx & 12,08
\end{array}\)](https://mathjax.schullv.de/4ef857f11270e586ccd3ae55555d17a66a2448f000c6bd2b5de392a6e5f2874b?color=5a5a5a) Auf
Auf  m ist ein Höhenunterschied von
m ist ein Höhenunterschied von  m zu überwinden. Mit der Trigonometrie ergibt sich:
m zu überwinden. Mit der Trigonometrie ergibt sich:
![\(\begin{array}[t]{rll}
\tan\varphi&=& \frac{d}{h} &\quad \scriptsize \mid\; \arctan\\[5pt]
\varphi&=& \arctan\left(\frac{12,08}{10}\right) \\[5pt]
&\approx & 50,38^\circ
\end{array}\)](https://mathjax.schullv.de/47e64eeea1f36fb4354c5366994c9e2893604144f07b6a588f6bd9cc51c26bcd?color=5a5a5a) Es ist eine Drehung um
Es ist eine Drehung um  notwendig.
notwendig.
 Ebenengleichung ermitteln
Du sollst eine Ebenengleichung für die Ebene durch die drei Punkte
Ebenengleichung ermitteln
Du sollst eine Ebenengleichung für die Ebene durch die drei Punkte  ,
,  und
und  ermitteln. Wähle
ermitteln. Wähle  als Stützpunkt. Für die Koordinatenform benötigst du den Normalenvektor, welchen du aus dem Kreuzprodukt der beiden Spannvektoren
als Stützpunkt. Für die Koordinatenform benötigst du den Normalenvektor, welchen du aus dem Kreuzprodukt der beiden Spannvektoren  und
und  erhältst. Den notwendigen Befehl findest du unter:
erhältst. Den notwendigen Befehl findest du unter:
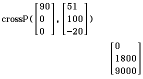 Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
Für die Normalenform einer Ebene kannst du ein Vielfaches des Normalenvektors verwenden. Du teilst somit jede Komponente des errechneten Vektors durch
Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
Für die Normalenform einer Ebene kannst du ein Vielfaches des Normalenvektors verwenden. Du teilst somit jede Komponente des errechneten Vektors durch  . Die Ebene ist somit von folgender Form:
. Die Ebene ist somit von folgender Form:
![\(\begin{array}[t]{rll}
d&=& 1\cdot x_2+5\cdot x_3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f52acc2de0bfdeea034bd9898e9ac5400f12d1ab497f290320cdfeef8347839a?color=5a5a5a) Um die Konstante
Um die Konstante  zu ermitteln, setzt du den Stützpunkt
zu ermitteln, setzt du den Stützpunkt  ein.
ein.
![\(\begin{array}[t]{rll}
d&=& 5\cdot 30 \\[5pt]
&=& 150
\end{array}\)](https://mathjax.schullv.de/1b7e5f42c3e7e19112249d09b38e9cc19392f385e937976f88573e754325c8ea?color=5a5a5a) Die Gleichung mit
Die Gleichung mit  bschriebt die Ebene durch die geforderten Punkte.
bschriebt die Ebene durch die geforderten Punkte.

 liegt unterhalb der Ebene nachweisen
Du sollst nachweisen, dass
liegt unterhalb der Ebene nachweisen
Du sollst nachweisen, dass  unterhalb der Ebene liegt. Dazu setzt du die
unterhalb der Ebene liegt. Dazu setzt du die  - und
- und  -Koordinaten in die Ebenengleichung ein und berechnest
-Koordinaten in die Ebenengleichung ein und berechnest  .
.
![\(\begin{array}[t]{rll}
150 &=& 70+5\cdot x_3 &\quad \scriptsize \mid\; -70 \\[5pt]
80&=& 5\cdot x_3 &\quad \scriptsize \mid\; :5 \\[5pt]
x_3&=& 16
\end{array}\)](https://mathjax.schullv.de/1d22287444c8023ac952b6a6bc1d5133dfd6a51ce0c9834bb6cf1c1c69ba06e2?color=5a5a5a) Die
Die  -Koordinate des Punktes in der Ebene mit
-Koordinate des Punktes in der Ebene mit  und
und  beträgt
beträgt  . Die
. Die  -Koordinate von
-Koordinate von  beträgt allerdings nur
beträgt allerdings nur  , somit liegt
, somit liegt  unterhalb der Ebene.
unterhalb der Ebene.
 Schlussfolgerung falsifizieren
Du sollst plausible machen, dass im Allgemeinen die Aussage falsch ist, dass wenn der höchste Punkt der Flugbahn eines Balles unterhalb von
Schlussfolgerung falsifizieren
Du sollst plausible machen, dass im Allgemeinen die Aussage falsch ist, dass wenn der höchste Punkt der Flugbahn eines Balles unterhalb von  liegt er die Seile nicht berühren kann. Dazu betrachtest du eine Schuss welcher bei
liegt er die Seile nicht berühren kann. Dazu betrachtest du eine Schuss welcher bei  in Richtung
in Richtung  abgestoßen wird.
Sein höchster Punkt liegt beispielsweise bei
abgestoßen wird.
Sein höchster Punkt liegt beispielsweise bei  und somit unterhalb der Eben, aber durch seine Parabel-Flugbahn landet er gleich daraufhin im Seil.
Bildnachweise [nach oben]
und somit unterhalb der Eben, aber durch seine Parabel-Flugbahn landet er gleich daraufhin im Seil.
Bildnachweise [nach oben]
a)
Interactive  Vector
Vector  crossP
crossP
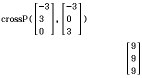 Abb. 1: Kreuzprodukt mit dem Classpad berechnen
Abb. 1: Kreuzprodukt mit dem Classpad berechnen
b)
c)
Interactive  Vector
Vector  norm
norm
Die Vektoren zwischen den Punkten ermittelst du wie zuvor.
 Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Abb. 2: Betrag bzw. Norm eines Vektors berechnen
Interactive  Vector
Vector  dotP
dotP
Betrachte die Vektoren  Abb. 3: Skalarprodukt berechnen
Abb. 3: Skalarprodukt berechnen
d)
e)
f)
g)
a)
Interactive  Vector
Vector  norm
norm
Für die Vektoren ergibt sich der Abstand zu 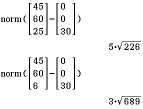 Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
Abb. 4: Länge eines Vektors mit dem norm-Befehl bestimmen
b)
c)
Keyboard  Math1
Math1
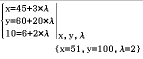 Abb. 5: Lineares Gleichungssystem lösen
Abb. 5: Lineares Gleichungssystem lösen
d)
e)
Interactive  Vector
Vector  crossP
crossP
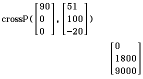 Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
Abb. 6: Kreuzprodukt aus den zwei Spannvektoren bestimmen
f)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.