Analysis Prüfungsteil A

Aufgabengruppe 1

Gegeben ist die Funktion $f:x \mapsto \sqrt{1-\text{ln}\,x}$ mit maximaler Definitionsmenge $D$ .

Bestimme $D$ .

(2P)

Bestimme den Wert $x\in D$ mit $f(x)=2$ .

(2P)

Zeige, dass der Graph der in $\mathbb{R}$ definierten Funktion $g: x \mapsto x^2 \cdot \text{sin}\,x$ punktsymmetrisch bezüglich des Koordinatenursprungs ist, und gib den Wert des Integrals $\displaystyle\int_{-\pi}^{\pi}\,x^2\cdot \text{sin}\, x \; \mathrm dx$ an.

(3P)

Skizziere im Bereich $-1\leq x\leq 4$ den Graphen einer in $\mathbb{R}$ definierten Funktion $f$ mit den folgenden Eigenschaften:

$f$ ist nur an der Stelle $x = 3$ nicht differenzierbar.
$f(0) =2$ und für die Ableitung $f‘$ von $f$ gilt: $f‘(0)=-1$ .
Der Graph von $f$ ist im Bereich $-1\lt x\lt 3$ linksgekrümmt.

(3P)

Gegeben ist eine in $\mathbb{R}$ definierte ganzrationale Funktion $f$ dritten Grades, deren Graph $G_f$ an der Stelle $x = 1$ einen Hochpunkt und an der Stelle $x = 4$ einen Tiefpunkt besitzt.

Begründe, dass der Graph der Ableitungsfunktion $f‘$ von $f$ eine Parabel ist, welche die $x$ -Achse in den Punkten $(1\mid 0)$ und $(4\mid 0)$ schneidet und nach oben geöffnet ist.

(3P)

Begründe, dass $2,5$ die $x$ -Koordinate des Wendepunkts von $G_f$ ist.

(2P)

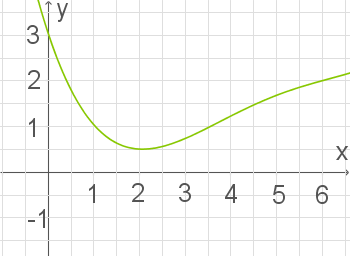
Die Abbildung 1 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ .

Graph einer Funktion mit einem grünen Verlauf auf einem karierten Hintergrund.

Abb. 1

Bestimme mithilfe der Abbildung 1 einen Näherungswert für $\displaystyle\int_{3}^{5}\, f(x)\,\mathrm dx$ .

(2P)

Die Funktion $F$ ist die in $\mathbb{R}$ definierte Stammfunktion von $f$ mit $F(3) =0$

Gib mithilfe der Abbildung 1 einen Näherungswert für die Ableitung von $F$ an der Stelle $x=2$ an.

(1P)

Zeige, dass $F(b)=\displaystyle\int_{3}^{b}f(x)\;\mathrm dx$ mit $b\in\mathbb{R}$ gilt.

(2P)

(20P)

Aufgabengruppe 2

Gegeben ist die Funktion $f:x \mapsto \dfrac{\mathrm{ln}x}{x^2}$ mit maximalem Definitionsbereich $D$ .

Gib $D$ sowie die Nullstelle von $f$ an und bestimme $\lim\limits_{x\to 0}\, f(x)$ .

(3P)

Ermittle die $x$ -Koordinate des Punkts, in dem der Graph von $f$ eine waagerechte Tangente hat.

(4P)

Gib jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.

Der Punkt $(2\mid 0)$ ist ein Wendepunkt des Graphen von $g$ .

(2P)

Der Graph der Funktion $h$ ist streng monoton fallend und rechtsgekrümmt.

(2P)

Abbildung 2 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ .

Abb. 2

Bestimme mithilfe von Abbildung 2 einen Näherungswert für $\displaystyle\int_{3}^{5}f(x)\;\mathrm dx$ .

(2P)

Die Funktion $F$ ist die in $\mathbb{R}$ definierte Stammfunktion von $f$ mit $F(3)=0$ .

Gib mithilfe von Abbildung 2 einen Näherungswert für die Ableitung von $F$ an der Stelle $x=2$ an.

(1P)

Zeige, dass $F(b)=\displaystyle\int_{3}^{b}f(x)\;\mathrm dx$ mit $x\in\mathbb{R}$ gilt.

(2P)

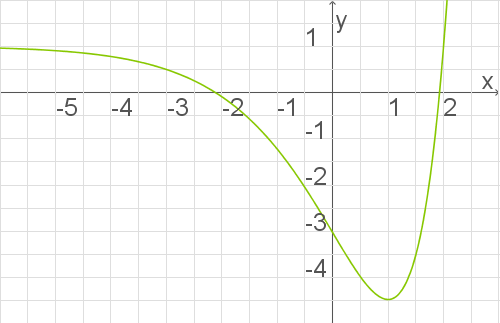
Abbildung 3 zeigt den Graphen $G_k$ einer in $\mathbb{R}$ definierten Funktion $k$ .
Skizziere in Abbildung 3 den Graphen der zugehörigen Ableitungsfunktion $k‘$ . Berücksichtige dabei insbesondere einen Näherungswert für die Steigung des Graphen $G_k$ an dessen Wendepunkt $(0 \mid -3)$ sowie die Nullstelle von $k‘$ .

Graph einer mathematischen Funktion auf einem Koordinatensystem mit Achsen und Gitterlinien.

Abb. 3

(4P)

(20P)

Bildnachweise [nach oben]

[1]

[2]

[3]

Aufgabengruppe 1

$\blacktriangleright$ Maximalen Definitonsbereich bestimmen

Du sollst den maximalen Definitionsbereich der Funktion $f:\, x\mapsto \sqrt{1-\ln x}$ bestimmen.
Hierzu betrachtest du zuerst das Argument der Wurzel: $1-\ln x$ . Dieses darf nicht negativ werden bzw. muss immer größer oder gleich $0$ sein.

$\begin{array}[t]{rll} 0&\leq & 1-\ln x &\quad \scriptsize \mid\; +\ln x \\[5pt] \ln x&\leq& 1 &\quad \scriptsize \mid\; e \\[5pt] x &\leq & e \end{array}$

Somit hast du $x$ zumindest auf einer Seite eingegrenzt. Ein weiteres Problem stellt der natürliche Logarithmus dar. Dessen Argument darf nicht negativ oder $0$ sein. Daraus erhältst du:

$\begin{array}[t]{rll} x&\gt & 0 \end{array}$

$x$ ist nun auf beiden Seiten durch Bedingungen eingeschränkt und du kannst den Definitionsbereich angeben:

$\begin{array}[t]{rll} D&=& ( 0,\,e ] \end{array}$

$\blacktriangleright$ Gleichung lösen

Du sollst die Stelle $x$ im Definitionsbereich bestimmen, für welche $f(x)=2$ gilt. Du erhältst folgende Gleichung:

$\begin{array}[t]{rll} 2&=& \sqrt{1-\ln x} &\quad \scriptsize \mid\; {}^2 \\[5pt] 4&=& 1-\ln x &\quad \scriptsize \mid\; +\ln x \; -4 \\[5pt] \ln x &=& -3 &\quad \scriptsize \mid\; e \\[5pt] x &=& e^{-3} \\[5pt] &\approx& 0,0498 \end{array}$

$x=0,0498$ ist Lösung der Gleichung und die gesuchte Stelle.

$\blacktriangleright$ Punktsymmetrie nachweisen

Du sollst nachweisen, dass der Graph der Funktion $g:\, x\mapsto x^2\cdot\sin x$ punktsymmetrisch zum Ursprung ist.
Für einen punktsymmetrischen Graphen gilt, für jede Stelle im Definitonsbereich, $g(-x)=-g(x)$ :

$\begin{array}[t]{rll} f(-x)&=& \quad ... \end{array}$

Vollständige Lösung anzeigen

Der Graph der Funktion $f$ ist somit punktsymmetrisch.

$\blacktriangleright$ Integral berechnen

Du sollst den Wert eines Integrals berechnen. Da die Bestimmung einer Stammfunktion schwierig ist, nutzt du die Punktsymmetrie des Graphen. Du teilst das Integral auf:

$\begin{array}[t]{rll} \int\limits_{-\pi}^\pi x^2\cdot \sin x\; dx&=& \quad ... \end{array}$

Vollständige Lösung anzeigen

Da der Graph punktsymmetrisch zum Ursprung ist, heben sich die Integrale gegenseitig auf:

$\begin{array}[t]{rll} \int\limits_{-\pi}^0 x^2\cdot \sin x\; dx + \int\limits_{0}^\pi x^2\cdot \sin x\; dx&=& 0 \\[5pt] \end{array}$

Der Wert des Integrals beträgt somit $0$ .

$\blacktriangleright$ Graph skizzieren

Du sollst den Graph einer Funktion skizzieren, welcher folgende Bedingungen erfüllt:

$f(x)$ ist auf $\mathbb{R}$ definiert.
$f$ ist nur an der Stelle $x=3$ nicht differenzierbar.
$f(0)=2$ und für die Ableitung $f‘$ von $f$ gilt: $f‘(0)=-1$ .
Der Graph von $f$ ist im Bereich $-1\lt x\lt 3$ linksgekrümmt.

Der erste Punkt bedeutet, dass $f$ an jeder Stelle einen Funktionswert besitzen muss. Da $f$ aber bei $x=3$ nicht differenzierbar sein soll, muss der Graph an dieser Stelle einen Knick aufweisen. Wähle also am besten eine zusammengesetzen Funktion, die aus zwei Teilen besteht.

Wegen des vierten Punkts, bietet sich für den Bereich $x \lt 3$ eine nach oben geöffnete Parabel an. Wegen der dritten Bedingung muss die Parabel durch den Punkt $P(0\mid2)$ verlaufen und dort die Steigung $-1$ besitzen. Letzteres bedeutet, dass es in diesem Punkt eine Tangente mit der Steigung $-1$ an die Parabel gibt. Die Tangente und den Punkt $P$ kannst du zur Orientierung in das Koordinatensystem einzeichnen.

Für den Bereich $x \geq 3$ ist nur wichtig, dass die Funktion in diesem Bereich keine Definitionslücken aufweist. Es kann sich also beispielsweise um eine Gerade handeln.

Foglendes Schaubild erfüllt beispielsweise alle Bedingungen:

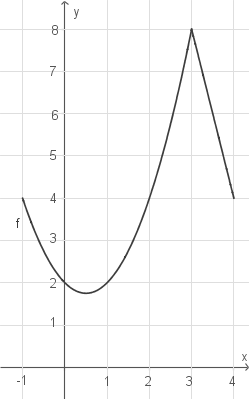Diagramm einer Parabel mit Achsenbeschriftungen x und y.

Abb. 1: Skizze des Funktionsgraphens

$\blacktriangleright$ Eigenschaften der Ableitung begründen

Du sollst begründen, dass die Ableitung von $f$ eine Parabel ist, sowie die Nullstellen $1$ und $4$ besitzt und nach oben geöffnet ist. Dazu überlegst du, was diese Bedingungen der Ableitung für den Graphen bedeuten.

Ist die Ableitung eine Parabel, also eine Funktion von Grad $2$ , so ist die Funktion von Grad $3$ .
Eine Nullstelle der Ableitung bedeutet für den Graphen einen Extrempunkt.
Nach oben geöffnet, bedeutet, dass die Ableitung für betragsmäßig große $x$ positiv ist. Die Funktion steigt für diese $x$ . Daraus schließt du, dass $f(x)\overset{x\rightarrow\infty}{\longrightarrow}\infty$ und $f(x)\overset{x\rightarrow -\infty}{\longrightarrow} -\infty$ gilt.

Betrachtest du nun den Hochpunkt an der Stelle $x=1$ und den Tiefpunkt an der Stelle $x=4$ , ist die erste Bedingung erfüllt. Die zweite Bedingung folgt direkt aus dem Aufgabentext. Abschließend überlegst du, wie die Funktion verläuft. Sie besitzt für $x=1$ einen Hochpunkt, insbesondere fällt sie davor. An der Stelle $x=4$ liegt ein Hochpunkt des Graphen vor. Die Funktion steigt danach weiter. Da eine Funktion dritten Grades maximal zwei Extrempunkte besitzen kann, kann es weiter rechts und links der beiden Extremstellen keine weiteren Extremstellen geben. Damit für $x=1$ ein Hochpunkt vorliegt, muss $f‘$ nach oben geöffnet sein.

$\blacktriangleright$ Wendestelle begründen

Du sollst begründen, dass $x=2,5$ die Wendestelle des Graphen von $f$ ist. Dazu nutzt du aus, dass die Ableitung eine Parabel und somit symmetrisch ist. Die einzige Stelle einer Parabel, welche die Steigung $0$ besitzt, liegt genau zwischen den zwei Nullstellen. Die Wendestelle des Graphen von $f$ dementsprechend auch. Du berechnest somit das arithmetische Mittel der beiden Nullstellen für die Wendestelle $x_W$ .

$\begin{array}[t]{rll} x_W&=& \frac{1+4}{2} \\[5pt] &=& \frac{5}{2}=2,5 \end{array}$

Somit liegt die Wendestelle des Graphen von $f$ bei $x=2,5$ .

$\blacktriangleright$ Näherungswert des Integrals bestimmen

Du sollst anhand des Funktionsgraphen einen Näherungswert für das Integral mit den Grenzen $3$ und $5$ bestimmen.

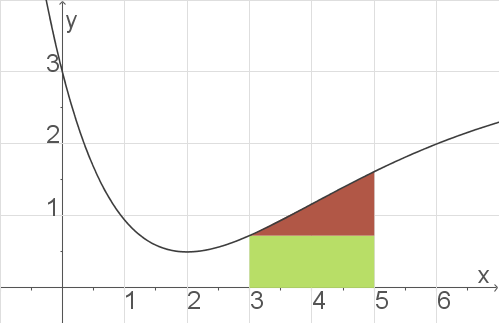Diagramm einer Funktion mit einem hervorgehobenen Bereich in verschiedenen Farben. Achsen sind beschriftet.

Abb. 2: Näherung des Integrals

Dazu zerlegst du die Fläche in Drei- und Vierecke. Die Näherung entspricht somit der Summe der Flächeninhalte. Für das Viereck mit den Kantenlängen $5-3=2$ und $f(3)$ ergibt sich:

$\begin{array}[t]{rll} A_{4}&=& 2\cdot f(3) \\[5pt] &\approx& 2\cdot 0,75 \\[5pt] &=& 1,5 \end{array}$

Das auf dem Viereck sitzende rechtwinklige Dreieck hat die lange Seite mit dem Viereck gemeinsam. Die Länge der kurzen Seite ist $f(5)-f(3)$ :

$\begin{array}[t]{rll} A_3&=& \frac{1}{2}\cdot 2\cdot (f(5)-f(3)) \\[5pt] &=& f(5)-f(3) \\[5pt] &\approx& 1,6-0,75 \\[5pt] &=& 0,85 \end{array}$

Für beide Flächen zusammen, beziehungsweise für die Näherung des Integrals, ergibt sich:

$\begin{array}[t]{rll} \int\limits_3^5 f(x)\; dx&\approx& A_4+A_3 \\[5pt] &=& 2,35 \end{array}$

Du kannst einen Näherungswert für das Integral mit ungefähr $2,35$ angeben.

$\blacktriangleright$ Wert der Ableitung bestimmen

Du sollst einen Wert für die Ableitung der Stammfunktion $F$ an der Stelle $x=2$ angeben. Da $F$ eine Stammfunktion von $f$ mit $F(3)=0$ ist, gilt:

$\begin{array}[t]{rll} F(x)&=&\int f(x)\, dx +c \\[5pt] F‘(x)&=& \frac{d}{dx}\left(\int f(x)\, dx \right)+c \\[5pt] &=& f(x) \end{array}$

Du kannst somit die Ableitung am Funktionsgraphen ablesen und erhältst:

$\begin{array}[t]{rll} F‘(2)&=& f(2) \\[5pt] &=& 0,5 \end{array}$

Die Ableitung der Funktion $F$ an der Stelle $x=2$ beträgt $0,5$ .

$\blacktriangleright$ Gleichheit zeigen

Du sollst zeigen, dass $F(b)=\int\limits_3^b f(x)\; dx$ gilt. Dazu betrachtest du die zwei Intervalle links und rechts von $b=3$ und genau die Stelle $b=3$ .

1. Schritt: Integral an der Stelle $b=3$

Für $x=3$ kennst du den Funkitonswert aus der Aufgabenstellung und prüfst diesen nach, dazu verwendest du den Hauptsatz der Integralrechnung:

$\begin{array}[t]{rll} F(3)&=& \int\limits_3^3 f(x) \; dx \\[5pt] &=& 0 \end{array}$

Dies entspricht der Definition von $F$ und ist somit korrekt.

2. Schritt: Integral für $b\gt 3$

Als nächstes betrachtest du das Intervall $(3,\infty)$ . In diesem Bereich entspricht das Integral, und somit der Funktionswert, der Fläche unter $f$ . Die Gleichheit ist per Definition gezeigt.

3. Schritt: Integral für $b\lt 3$

Im Intervall $(-\infty,3)$ ist das Integral, wie es gegeben ist, nicht berechenbar und du verwendest erst den Hauptsatz der Integralrechnung:

$\begin{array}[t]{rll} F(b)&=& \int\limits_3^b f(x)\; dx &\quad \scriptsize \mid\; b\lt 3 \\[5pt] &=& -\int\limits_b^3 f(x)\; dx \end{array}$

Für $b\lt 3$ wird der Funktionswert durch Subtraktion des Flächeninhaltes berechnet, was der Aussage entspricht.

Aufgabengruppe 2

$\blacktriangleright$ Definitionsbereich bestimmen

Du sollst den Definitionsbereich $D$ sowie die Nullstellen und den Grenzwert der Funktion $f:\, x\mapsto\dfrac{\ln x}{x^2}$ bestimmen. Für den Definitionsbereich betrachtest du zuerst den Nenner $x^2$ .

$\dfrac{1}{x^2}$ ist für alle $x$ außer $0$ definiert. Du erhältst einen ersten Definitionsbereich von $D_1=\mathbb{R}\setminus \{0\}$ .
Im Zähler $\ln x$ dürfen nur strickt positive Argumente verwendet werden, der Definitionsbereich des $\ln$ ist $D_2=\mathbb{R}^+=(0,\infty)$ .

Zusammenfassend ergibt sich für den gesuchten Definitionsbereich $D$ :

$\begin{array}[t]{rll} D&=& D_1\cup D_2 \\[5pt] &=& \mathbb{R}^+=(0,\infty) \end{array}$

$\blacktriangleright$ Nullstellen bestimmen

Für die Nullstellen der Funktion sind lediglich die Nullstellen des Zählers zu betrachten:

$\begin{array}[t]{rll} \ln x&=& 0 &\quad \scriptsize \mid\; e \\[5pt] x&=& e^0=1 \end{array}$

$x=1$ ist die einzige Nullstelle des $\ln$ und liegt im Definitionsbereich $D$ , somit ist es auch Nullstelle von $f$ .

$\blacktriangleright$ Grenzwert bestimmen

Du sollst den Grenzwert von $f(x)$ für $x\to 0$ bestimmen. Der Funktionsterm besteht aus einem Bruch. Überlege dir für die beiden Terme im Zähler und Nenner zunächst unabhängig den Grenzwert für $x\to 0$ .

Im Zähler steht $\ln(x)$ . Für $x=0$ ist dies nicht definiert. Du kennst aber den groben Verlauf der Logarithmusfunktion und weißt daher, dass $\ln(x)$ für $x \lt 1$ negativ ist und für immer kleinere $x$ auch immer kleiner wird, und zwar unbegrenzt. Daher gilt
$\lim\limits_{x\to0} \ln(x) = -\infty$

Im Nenner des Bruchs steht $x^2$ . Dies ist definiert, es ist $0^2 = 0$ . Es wird also sozusagen $-\infty$ durch $0$ geteilt. Es kann aber nicht durch $0$ geteilt werden. Betrachtest du also den Grenzwert, wird $-\infty$ durch einen sehr kleinen aber positiven Wert geteilt. Und daher ist:

$\lim\limits_{x\to0} \dfrac{\ln(x)}{x^2} = -\infty$ .

$\blacktriangleright$ Stelle mit waagerechter Tangente bestimmen

Du sollst die $x$ -Koordinate der Stelle bestimmen, an welcher der Graph eine waagerechte Tangente besitzt. Waagerechte Tangenten besitzen die Steigung $0$ . Somit suchst du eine Nullstelle der Ableitung, welche du über die Quotientenregel erhältst:

$\dfrac{d}{dx}\dfrac{u(x)}{v(x)}=\dfrac{u‘(x)\cdot v(x)-u(x)\cdot v‘(x)}{(v(x))^2}$

Mit $u(x)=\ln x$ und $v(x)=x^2$ ergibt sich:

$\begin{array}[t]{rll} f‘(x)&=& \dfrac{\dfrac{1}{x}\cdot x^2-\ln x \cdot 2\cdot x}{x^4} \\[5pt] &=& \dfrac{1-2\cdot \ln x}{x^3} \end{array}$

Für die Nullstelle betrachtest du lediglich den Zähler:

$\begin{array}[t]{rll} 0&=& 1-2\cdot \ln x &\quad \scriptsize \mid\; +2\cdot \ln x \\[5pt] 1&=& 2\cdot \ln x &\quad \scriptsize \mid\; :2 \\[5pt] \frac{1}{2}&=&\ln x &\quad \scriptsize \mid\; e \\[5pt] x&=&\sqrt{e} \end{array}$

Für $x=\sqrt{e}$ besitzt der Graph von $f$ eine waagerechte Tangente.

$\blacktriangleright$ Term und Definitionsbereich angeben

Du sollst den Term und den Definitionsbereich einer Funktion angeben, welche die Eigenschafft erfüllt, dass $(2\vert 0)$ ein Wendepunkt des Graphen von $g$ ist.

Für einen Wendepunkt muss die zweite Ableitung $0$ , aber nicht konstant sein. Die einfachste Form ist deshalb die Verschiebung einer Geraden. Du erhältst durch Integration, wobei $c=0$ ist:

$\begin{array}[t]{rll} g‘‘(x)&=& x-2 \\[5pt] g‘(x)&=& \frac{1}{2}\cdot x^2-2\cdot x \\[5pt] g(x)&=& \frac{1}{6}\cdot x^3 -x^2 \end{array}$

Der Graph von $g$ besitzt an der Stelle $x=2$ einen Wendepunkt. Dieser hat aber noch nicht die $y$ -Koordinate null:

$g(2)= \frac{1}{6}\cdot 2^3-2^2 =-\frac{8}{3}$

Der Graph muss also noch um $\frac{8}{3}$ Einheiten entlang der positiven $y$ -Achse verschoben werden.

Die Funktion $g_1(x)=\frac{1}{6}\cdot x^3 -x^2+\frac{8}{3}$ erfüllt die Bedingung, wobei für den Definitionsbereich $D=\mathbb{R}$ gilt.

$\blacktriangleright$ Term und Definitionsbereich angeben

Der Graph der Funktion $h$ soll streng monoton fallend und rechtsgekrümmt sein. Die Rechtskrümmung ergibt sich durch eine immer negative Ableitung, setzt diese deshalb auf $h‘‘(x)=1$ . Durch Integration erhältst du:

$\begin{array}[t]{rll} h‘(x)&=& -x \\[5pt] h(x)&=& -\frac{1}{2}\cdot x^2 \end{array}$

Da allerdings $h(x)=-\frac{1}{2}\cdot x^2$ nur für positive $x$ streng monoton fällt, ergibt sich eine Definitionsbereich von $D=\mathbb{R}^+$ .

$\blacktriangleright$ Näherungswert des Integrals bestimmen

Du sollst anhand des Funktionsgraphen einen Näherungswert für das Integral mit den Grenzen $3$ und $5$ bestimmen.

Abb. 2: Näherung des Integrals

Dazu zerlegst du die Fläche in Drei- und Vierecke. Die Näherung entspricht somit der Summe der Flächeninhalte. Für das Viereck mit den Kantenlängen $5-3=2$ und $f(3)$ ergibt sich:

$\begin{array}[t]{rll} A_{4}&=& 2\cdot f(3) \\[5pt] &\approx& 2\cdot 0,75 \\[5pt] &=& 1,5 \end{array}$

Das auf dem Viereck sitzende rechtwinklige Dreieck hat die lange Seite mit dem Viereck gemeinsam. Die Länge der kurzen Seite ist $f(5)-f(3)$ :

$\begin{array}[t]{rll} A_3&=& \frac{1}{2}\cdot 2\cdot (f(5)-f(3)) \\[5pt] &=& f(5)-f(3) \\[5pt] &\approx& 1,6-0,75 \\[5pt] &=& 0,85 \end{array}$

Für beide Flächen zusammen, beziehungsweise für die Näherung des Integrals, ergibt sich:

$\begin{array}[t]{rll} \int\limits_3^5 f(x)\; dx&\approx& A_4+A_3 \\[5pt] &=& 2,35 \end{array}$

Du kannst einen Näherungswert für das Integral mit ungefähr $2,35$ angeben.

$\blacktriangleright$ Wert der Ableitung bestimmen

Du sollst einen Wert für die Ableitung der Stammfunktion $F$ an der Stelle $x=2$ angeben. Da $F$ eine Stammfunktion von $f$ mit $F(3)=0$ ist, gilt:

$\begin{array}[t]{rll} F(x)&=&\int f(x)\, dx +c \\[5pt] F‘(x)&=& \frac{d}{dx}\left(\int f(x)\, dx \right)+c \\[5pt] &=& f(x) \end{array}$

Du kannst somit die Ableitung am Funktionsgraphen ablesen und erhältst:

$\begin{array}[t]{rll} F‘(2)&=& f(2) \\[5pt] &=& 0,5 \end{array}$

Die Ableitung der Funktion $F$ an der Stelle $x=2$ beträgt $0,5$ .

$\blacktriangleright$ Gleichheit zeigen

Du sollst zeigen, dass $F(b)=\int\limits_3^b f(x)\; dx$ gilt. Dazu betrachtest du die zwei Intervalle links und rechts von $b=3$ und genau die Stelle $b=3$ .

1. Schritt: Integral an der Stelle $b=3$

Für $x=3$ kennst du den Funkitonswert aus der Aufgabenstellung und prüfst diesen nach, dazu verwendest du den Hauptsatz der Integralrechnung:

$\begin{array}[t]{rll} F(3)&=& \int\limits_3^3 f(x) \; dx \\[5pt] &=& 0 \end{array}$

Dies entspricht der Definition von $F$ und ist somit korrekt.

2. Schritt: Integral für $b\gt 3$

Als nächstes betrachtest du das Intervall $(3,\infty)$ . In diesem Bereich entspricht das Integral, und somit der Funktionswert, der Fläche unter $f$ . Die Gleichheit ist per Definition gezeigt.

3. Schritt: Integral für $b\lt 3$

Im Intervall $(-\infty,3)$ ist das Integral, wie es gegeben ist, nicht berechenbar und du verwendest erst den Hauptsatz der Integralrechnung:

$\begin{array}[t]{rll} F(b)&=& \int\limits_3^b f(x)\; dx &\quad \scriptsize \mid\; b\lt 3 \\[5pt] &=& -\int\limits_b^3 f(x)\; dx \end{array}$

Für $b\lt 3$ wird der Funktionswert durch Subtraktion des Flächeninhaltes berechnet, was der Aussage entspricht.

$\blacktriangleright$ Ableitung skizzieren

Du sollst zu einem gegebenen Funktionsgraphen die Ableitung skizzieren und dabei besonders auf die Steigung am Wendepunkt $(0\vert -3)$ achten. Zeichne dir idealerweise ein paar Tangenten an den Graphen und markiere signifikante Stellen wie Wende- und Extremalstellen.

Da der Graph gegen eine waagerechte Asymptote bei $y=1$ strebt, konvergiert die Ableitung gegen $0$ . Für die Wendestelle bei $x=0$ ergibt sich in der Ableitung ein Tiefpunkt, wobei dieser bei ungefähr $y=2$ liegt. Danach steigt die Ableitung, wie die Funktion, stetig weiter. Skizziert ergibt sich in grün die Ableitung:

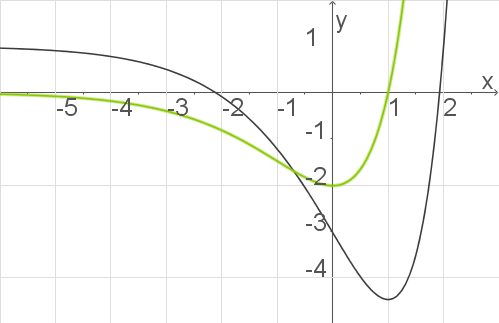Graph zweier Funktionen im Koordinatensystem mit x- und y-Achse.

Abb. 3: Ableitung skizzieren