Analysis Prüfungsteil B
Aufgabengruppe 1
1
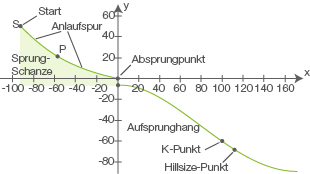
Der höchste Punkt der Anlaufspur wird durch den Punkt  dargestellt. Die Anlaufspur verläuft im Modell zwischen den Punkten
dargestellt. Die Anlaufspur verläuft im Modell zwischen den Punkten  und
und  entlang einer Geraden, die gegenüber der
entlang einer Geraden, die gegenüber der  -Achse um
-Achse um  geneigt ist.
geneigt ist.
Der Aufsprunghang beginnt im Modell im Punkt
a)
Bestimme eine Gleichung der Geraden durch  und
und  . Runde im Ergebnis auf eine Nachkommastelle.
. Runde im Ergebnis auf eine Nachkommastelle.
(3P)
b)
Die Punkte  und
und  liegen in der Realität
liegen in der Realität  voneinander entfernt.
voneinander entfernt.
Berechne die Koordinaten von auf eine Nachkommastelle genau.
auf eine Nachkommastelle genau.
Berechne die Koordinaten von
(4P)
beschreiben.
2
a)
Gib die Höhe des Absprungpunkts über dem Beginn des Aufsprunghangs sowie die Steigung des Aufsprunghangs in seinem Beginn an.
(2P)
b)
Derjenige Punkt, in dem die Profillinie im unteren Bereich des Aufsprunghangs einen Neigungswinkel von  gegenüber der Horizontalen aufweist, wird als Hillsize-Punkt bezeichnet (vgl. Abbildung). Die Größe einer Skisprunganlage wird durch die Länge der Strecke zwischen dem Absprungpunkt und dem Hillsize-Punkt festgelegt und als Hillsize bezeichnet.
gegenüber der Horizontalen aufweist, wird als Hillsize-Punkt bezeichnet (vgl. Abbildung). Die Größe einer Skisprunganlage wird durch die Länge der Strecke zwischen dem Absprungpunkt und dem Hillsize-Punkt festgelegt und als Hillsize bezeichnet.
Bestimme auf der Grundlage des Modells die Hillsize auf Meter genau und berechne deren prozentuale Abweichung von der tatsächlichen Hillsize dieser Skisprunganlage, die beträgt.
beträgt.
Bestimme auf der Grundlage des Modells die Hillsize auf Meter genau und berechne deren prozentuale Abweichung von der tatsächlichen Hillsize dieser Skisprunganlage, die
(8P)
3
Zur Beschreibung der Flugkurve eines Skispringers wird die in  definierte Funktion
definierte Funktion  verwendet. Dabei ist die Sprungweite die Länge der Profillinie des Aufsprunghangs zwischen dem Punkt
verwendet. Dabei ist die Sprungweite die Länge der Profillinie des Aufsprunghangs zwischen dem Punkt  und dem Punkt
und dem Punkt  , der den Landepunkt des Skispringers auf dem Aufsprunghang beschreibt.
, der den Landepunkt des Skispringers auf dem Aufsprunghang beschreibt.
 bezeichnete Länge des Graphen der Funktion
bezeichnete Länge des Graphen der Funktion  zwischen den Punkten
zwischen den Punkten  und
und  mit
mit  kann mithilfe der Formel
kann mithilfe der Formel ![\(l=\displaystyle\int_{a}^{b}\sqrt{1+[h‘(x)]^2]}\;\mathrm dx\)](https://mathjax.schullv.de/b909c31a1003cdeca596d2240e2098de0938292abf129ed305829f739d1d9591?color=5a5a5a) berechnet werden.
Hinweis: Führe die Berechnungen in den Aufgaben 3b und 3c mit dem CAS jeweils näherungsweise durch!
berechnet werden.
Hinweis: Führe die Berechnungen in den Aufgaben 3b und 3c mit dem CAS jeweils näherungsweise durch!
 -Punkt (kritischer Punkt) der hier betrachteten Skisprunganlage liegt so auf der Profillinie, dass die Kurvenlänge zwischen ihm und dem Beginn des Aufsprunghangs, die sogenannte
-Punkt (kritischer Punkt) der hier betrachteten Skisprunganlage liegt so auf der Profillinie, dass die Kurvenlänge zwischen ihm und dem Beginn des Aufsprunghangs, die sogenannte  -Punkt-Weite,
-Punkt-Weite,  beträgt.
beträgt.
a)
Bestimme die Koordinaten des Punkts  auf eine Nachkommastelle genau.
auf eine Nachkommastelle genau.
Die als Kurvenlänge
(Teilergebnis:  -Koordinate des Punktes
-Koordinate des Punktes  )
)
(2P)
b)
Bestimme die Sprungweite des Skispringers; berücksichtige dabei, dass beim Skispringen Sprungweiten nur auf halbe Meter genau angegeben werden.
Der
(Ergebnis:  )
)
(3P)
c)
Ermittle die Koordinaten des  -Punkts auf eine Nachkommastelle genau.
-Punkts auf eine Nachkommastelle genau.
(4P)
d)
Für einen Sprung auf den  -Punkt einer Skisprunganlage bekommt ein Springer
-Punkt einer Skisprunganlage bekommt ein Springer  Weitenpunkte. Für jeden halben Meter, den er kürzer bzw. weiter springt, werden Weitenpunkte gemäß nachstehender Tabelle subtrahiert bzw. addiert. Bestimme die Gesamtzahl der Weitenpunkte für den betrachteten Sprung.
Weitenpunkte. Für jeden halben Meter, den er kürzer bzw. weiter springt, werden Weitenpunkte gemäß nachstehender Tabelle subtrahiert bzw. addiert. Bestimme die Gesamtzahl der Weitenpunkte für den betrachteten Sprung.
der Sprunganlage in Metern |
Weitenpunkte pro halbem Meter |
|---|---|
| 70-79 | 1,1 |
| 80-99 | 1,0 |
| 100-169 | 0,9 |
| ab 170 | 0,6 |
(3P)
e)
Die Landung ist für den Springer umso schwieriger, je größer der Winkel zwischen Aufsprunghang und Flugkurve im Landepunkt ist. Berechne die Größe dieses Winkels für den betrachteten Sprung.
(4P)
f)
Formuliere im Sachzusammenhang eine Aufgabenstellung, die mit folgendem Lösungsweg gelöst werden kann.



 Der gesuchte Wert beträgt etwa
Der gesuchte Wert beträgt etwa  .
.
(3P)
g)
Zur Beschreibung der Flugkurve eines zweiten Skispringers wird die in  definierte Funktion
definierte Funktion  verwendet. Dabei gilt
verwendet. Dabei gilt
 und
und  .
Entscheide jeweils, welcher der beiden Skispringer unter einem betragsmäßig größeren Winkel gegenüber der Horizontalen abspringt und welcher die größere Sprungweite erzielt. Begründe deine Entscheidungen.
.
Entscheide jeweils, welcher der beiden Skispringer unter einem betragsmäßig größeren Winkel gegenüber der Horizontalen abspringt und welcher die größere Sprungweite erzielt. Begründe deine Entscheidungen.
(4P)
(40P)
Aufgabengruppe 2
1
Gegeben ist die Funktion  mit maximalem Definitionsbereich
mit maximalem Definitionsbereich  .
.
Der Graph von wird mit
wird mit  bezeichnet.
bezeichnet.
Der Graph von
a)
Gib  , den Wertebereich
, den Wertebereich  von
von  sowie die Gleichungen aller Asymptoten von
sowie die Gleichungen aller Asymptoten von  an.
an.
(4P)
b)
Der Graph der Funktion  geht aus
geht aus  durch eine Verschiebung hervor und ist symmetrisch bezüglich des Koordinatenursprungs. Gib eine Gleichung von
durch eine Verschiebung hervor und ist symmetrisch bezüglich des Koordinatenursprungs. Gib eine Gleichung von  an.
an.
(2P)
c)
Die Funktion  ist umkehrbar. Beschreibe, wie man den Term der Umkehrfunktion von
ist umkehrbar. Beschreibe, wie man den Term der Umkehrfunktion von  bestimmen kann, und gib Definitions- und Wertebereich der Umkehrfunktion von
bestimmen kann, und gib Definitions- und Wertebereich der Umkehrfunktion von  an.
an.
(3P)
d)
Der Graph der Funktion  und der Graph der Umkehrfunktion von
und der Graph der Umkehrfunktion von  schneiden sich im Koordinatenursprung. Bestimme die Größe des Winkels, den die beiden Graphen im Koordinatenursprung einschließen.
schneiden sich im Koordinatenursprung. Bestimme die Größe des Winkels, den die beiden Graphen im Koordinatenursprung einschließen.
(4P)
e)
Die Punkte  und
und  mit
mit  sind Eckpunkte eines Rechtecks, dessen Seiten parallel zur
sind Eckpunkte eines Rechtecks, dessen Seiten parallel zur  Achse bzw. zur
Achse bzw. zur  Achse sind. Das Rechteck wird von
Achse sind. Das Rechteck wird von  in zwei Teilflächen gleichen Inhalts zerlegt. Bestimme einen Näherungswert für
in zwei Teilflächen gleichen Inhalts zerlegt. Bestimme einen Näherungswert für  auf zwei Dezimalen genau.
auf zwei Dezimalen genau.
(4P)
2
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit  .
.
a)
Begründe ausschließlich anhand des Funktionsterms  , ohne Verwendung von Ableitungen, dass alle Funktionen
, ohne Verwendung von Ableitungen, dass alle Funktionen  an der Stelle
an der Stelle  ein Minimum besitzen.
ein Minimum besitzen.
(2P)
b)
Weise nach, dass alle Wendepunkte der Graphen der Schar  auf einer Parallelen zur
auf einer Parallelen zur  Achse liegen.
Achse liegen.
(4P)
c)
In dieser Aufgabe ist  . Für jedes
. Für jedes  legen die Punkte
legen die Punkte  ,
,  und
und  das Dreieck
das Dreieck  fest. Bestimme dessen Flächeninhalt
fest. Bestimme dessen Flächeninhalt  in Abhängigkeit von
in Abhängigkeit von  und ermittle anschließend denjenigen Wert von
und ermittle anschließend denjenigen Wert von  , für den der Flächeninhalt des zugehörigen Dreiecks maximal ist.
, für den der Flächeninhalt des zugehörigen Dreiecks maximal ist.
(Teilergebnis:  )
)
(5P)
3
Betrachtet wird die in  definierte Funktion
definierte Funktion  .
.
 und eine Dicke von
und eine Dicke von  Es wird in einer Maschine zu einem Wellblechelement mit unverändertem Volumen umgeformt (vgl. Abbildung 2).
Von oben betrachtet deckt das Wellblechelement weiterhin ein Quadrat der Seitenlänge
Es wird in einer Maschine zu einem Wellblechelement mit unverändertem Volumen umgeformt (vgl. Abbildung 2).
Von oben betrachtet deckt das Wellblechelement weiterhin ein Quadrat der Seitenlänge  ab, seine mittlere Dicke ist folglich geringer als
ab, seine mittlere Dicke ist folglich geringer als  . Die Profillinie des Wellblechelements (vgl. Abbildung 3) kann durch ein Teilstück des Graphen von
. Die Profillinie des Wellblechelements (vgl. Abbildung 3) kann durch ein Teilstück des Graphen von  beschrieben werden; eine Längeneinheit im Koordinatensystem entspricht dabei
beschrieben werden; eine Längeneinheit im Koordinatensystem entspricht dabei  in der Realität.
in der Realität.
Bildnachweise [nach oben]
a)
Zeichne den Graphen der Funktion  im Intervall
im Intervall ![\([-25;175]\)](https://mathjax.schullv.de/8463076ca7f4550e55bb03576999b4797a140a99d30133a963eec0713dab37ec?color=5a5a5a) in ein geeignet skaliertes Koordinatensystem ein.
in ein geeignet skaliertes Koordinatensystem ein.
(2P)
b)
Gib an, wie der Graph der Funktion  schrittweise aus dem Graphen der in
schrittweise aus dem Graphen der in  definierten Funktion
definierten Funktion  hervorgeht.
hervorgeht.
Ein quaderförmiges Aluminiumblech besitzt eine quadratische Grundfläche der Seitenlänge
(2P)
c)
Bestimme die mittlere Dicke des Wellblechelements auf Zehntelmillimeter genau. Verwende dabei, dass für die Länge  des Funktionsgraphen der Funktion
des Funktionsgraphen der Funktion  zwischen den Punkten
zwischen den Punkten  und
und  mit
mit  gilt:
gilt: ![\(l=\displaystyle\int_{a}^{b}\sqrt{1+[w‘(x)]^2}\;\mathrm dx\)](https://mathjax.schullv.de/7ceedc0f5443635be6467ee2e5885c4bf863b68f1fe38f1761d9671114e1f957?color=5a5a5a) .
.
(4P)
d)
Das Wellblechelement wird auf einer ebenen Dachfläche so angebracht, dass es unmittelbar aufliegt. Der dabei entstehende Hohlraum wird ausgeschäumt. Bestimme das Volumen, das der Schaum einnimmt; vernachlässige dabei die Dicke des Wellblechelements.
(4P)
(40P)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabengruppe 1
 Geradengleichung bestimmen
Du sollst die Gleichung einer Geraden durch die Punkte
Geradengleichung bestimmen
Du sollst die Gleichung einer Geraden durch die Punkte  und
und  bestimmen. Das Problem hierbei liegt darin, dass dir die Koordinaten des Punktes
bestimmen. Das Problem hierbei liegt darin, dass dir die Koordinaten des Punktes  nicht bekannt sind. Allerdings kannst du mit dem angegebenen Winkel von
nicht bekannt sind. Allerdings kannst du mit dem angegebenen Winkel von  und dem Winkelsatz
und dem Winkelsatz  auf die Steigung der Geraden schließen.
auf die Steigung der Geraden schließen.
![\(\begin{array}[t]{rll}
m&=& \tan( -35^\circ) \\[5pt]
&\approx& -0,7
\end{array}\)](https://mathjax.schullv.de/9cc5e24f4a5eb6c42d7db684b577f7947a51cfa670adc87b0bd878912dd22c49?color=5a5a5a) Die Steigung beträgt
Die Steigung beträgt  somit kannst du eine Geradengleichung durch Verschiebung aufstellen.
somit kannst du eine Geradengleichung durch Verschiebung aufstellen.
![\(\begin{array}[t]{rll}
y=&=& -0,7\cdot (x+94)+51 \\[5pt]
&=& -0,7\cdot x-14,8
\end{array}\)](https://mathjax.schullv.de/745a9688efe24661984ac8958ff4d2cbac64c2ae561fa0d1b6cbf23cec03767d?color=5a5a5a) Diese Grade läuft durch die Punkte
Diese Grade läuft durch die Punkte  und
und  .
.
 Koordinaten von
Koordinaten von  bestimmen
Du sollst die Koordinaten des Punktes
bestimmen
Du sollst die Koordinaten des Punktes  auf eine Nachkommastelle genau bestimmen. Du kennst die Geradengleichung und den Abstand der beiden Punkte. Mit dem Pythagoras kannst du ein Gleichungssystem aufstellen:
auf eine Nachkommastelle genau bestimmen. Du kennst die Geradengleichung und den Abstand der beiden Punkte. Mit dem Pythagoras kannst du ein Gleichungssystem aufstellen:
![\(\begin{array}[t]{rll}
50^2&=& (-94-x)^2+(51-y)^2 \\[5pt]
y&=& -0,7\cdot x-14,8
\end{array}\)](https://mathjax.schullv.de/d89071e6ba7bbb4fc36d956bb1cd67cc3a925461d2451d6a5adee6b539594000?color=5a5a5a) Das Gleichungssystem löst du mit dem Befehl:
Das Gleichungssystem löst du mit dem Befehl:
 Abb. 1: Gleichungssystem lösen mit dem nspire
Es handelt sich um ein Gleichungssystem mit quadratischen Termen und du erhältst deshalb zwei Lösungen. Da
Abb. 1: Gleichungssystem lösen mit dem nspire
Es handelt sich um ein Gleichungssystem mit quadratischen Termen und du erhältst deshalb zwei Lösungen. Da  weiter rechts liegt als
weiter rechts liegt als  erhältst du
erhältst du  .
.
 Höhe des Absprungpunktes bestimmen
Du sollst den Höhenunterschied zwischen der Absprungkante und dem Beginn des Aufsprunghangs bestimmen. Die Absprungkante liegt im Koordinatenursprung
Höhe des Absprungpunktes bestimmen
Du sollst den Höhenunterschied zwischen der Absprungkante und dem Beginn des Aufsprunghangs bestimmen. Die Absprungkante liegt im Koordinatenursprung  , der Aufsprunghang beginnt im Punkt
, der Aufsprunghang beginnt im Punkt  .
Das einzige dir Unbekannte ist die
.
Das einzige dir Unbekannte ist die  -Koordinate von
-Koordinate von  , welche du mit
, welche du mit  berechnest:
Der gesuchte Abstand
berechnest:
Der gesuchte Abstand  berechnest du aus der Differenz der
berechnest du aus der Differenz der  -Koordinaten:
-Koordinaten:
![\(\begin{array}[t]{rll}
\Delta &=& 0-h(0) \\[5pt]
&=& 3,38
\end{array}\)](https://mathjax.schullv.de/20e30305c7b6ea2de1d3fcde84eb489a32797a9cfb415f0798a8b24d934040af?color=5a5a5a) Der Abstand zwischen Absprungkante und Aufsprunghang beträgt
Der Abstand zwischen Absprungkante und Aufsprunghang beträgt  m.
m.
 Hillsize und Abweichung zum Soll berechnen
Du sollst die Hillsize, das Maß für die Größe einer Skisprunganlage, berechnen. Du weißt, dass die Hillsize die Länge der Strecke zwischen dem Absprungpunkt und dem Hillsize-Punkt, welcher auf
Hillsize und Abweichung zum Soll berechnen
Du sollst die Hillsize, das Maß für die Größe einer Skisprunganlage, berechnen. Du weißt, dass die Hillsize die Länge der Strecke zwischen dem Absprungpunkt und dem Hillsize-Punkt, welcher auf  liegt, ist. Zuerst bestimmst du dementsprechend die Koordinaten des Hillsize-Punktes, dessen Steigung
liegt, ist. Zuerst bestimmst du dementsprechend die Koordinaten des Hillsize-Punktes, dessen Steigung  beträgt. Dazu verwendest du den Winkelsatz:
beträgt. Dazu verwendest du den Winkelsatz:
 1. Schritt: Stelle des Hillsize-Punktes bestimmen
Du suchst die Stelle
1. Schritt: Stelle des Hillsize-Punktes bestimmen
Du suchst die Stelle  für welche gilt:
für welche gilt:
![\(\begin{array}[t]{rll}
h‘(x_H)&=& \tan(-32^\circ) \\[5pt]
\end{array}\)](https://mathjax.schullv.de/5a2da93ca7fc8551f380be80854d8a5b93e45197bbd52a3539ce75a8900d7aea?color=5a5a5a) Diese Gleichung löst du mit:
Diese Gleichung löst du mit:
 Abb. 2: Gleichung lösen mit dem nspire
Du erhältst erneut zwei Lösungen, wobei du nur
Abb. 2: Gleichung lösen mit dem nspire
Du erhältst erneut zwei Lösungen, wobei du nur  beachtest.
2. Schritt: Hillsize-Punkt bestimmen
Aus der
beachtest.
2. Schritt: Hillsize-Punkt bestimmen
Aus der  -Koordinate bestimmst du den Hillsizepunkt
-Koordinate bestimmst du den Hillsizepunkt  .
Für
.
Für  ergeben sich die Koordinaten
ergeben sich die Koordinaten  .
3. Schritt: Abstand zum Absprungpunkt bestimmen
Jetzt ist es möglich den Abstand, also die Hillsize
.
3. Schritt: Abstand zum Absprungpunkt bestimmen
Jetzt ist es möglich den Abstand, also die Hillsize  , zum Absprungpunkt
, zum Absprungpunkt  zu bestimmen. Dazu verwendest du den Satz des Pythagoras.
Es ergibt sich eine Hillsize von
zu bestimmen. Dazu verwendest du den Satz des Pythagoras.
Es ergibt sich eine Hillsize von  m.
4. Schritt: Abweichung bestimmen
Du sollst die prozentuale Abweichung
m.
4. Schritt: Abweichung bestimmen
Du sollst die prozentuale Abweichung  zur tatsächlichen Hillsize von
zur tatsächlichen Hillsize von  m bestimmen.
m bestimmen.
![\(\begin{array}[t]{rll}
\delta&=& \frac{131-132}{132} \\[5pt]
&\approx & -7,58\cdot 10^{-3} = -0,758\%
\end{array}\)](https://mathjax.schullv.de/931ec0215de8db741eff62dcb769880fed5b51fd10f71c367a76a8495ae9215d?color=5a5a5a) Die Abweichung zur tatsächlichen Hillsize beträgt weniger
Die Abweichung zur tatsächlichen Hillsize beträgt weniger  .
.
 Koordinaten von
Koordinaten von  bestimmen
Du sollst die Koordinaten des Punktes
bestimmen
Du sollst die Koordinaten des Punktes  bestimmen, welcher den Landepunkt eines Springers mit der Flugbahn
bestimmen, welcher den Landepunkt eines Springers mit der Flugbahn  beschreibt. Du bestimmst somit den Schnittpunkt
beschreibt. Du bestimmst somit den Schnittpunkt  von
von  und
und  . Dazu verwendest du erneut den solve Befehl.
. Dazu verwendest du erneut den solve Befehl.
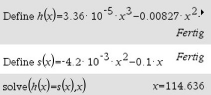 Abb. 3: Gleichung lösen mit dem nspire
Es ergibt sich
Abb. 3: Gleichung lösen mit dem nspire
Es ergibt sich  . Als zweites fehlt die
. Als zweites fehlt die  -Koordinate. Dazu kannst du sowohl die Funktion
-Koordinate. Dazu kannst du sowohl die Funktion  als auch
als auch  verwenden.
verwenden.
![\(\begin{array}[t]{rll}
s(114,6)&\approx& -66,6 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/930191f9a974648db4796b20a92d527e219d1d942a529bce0b747b323db9184b?color=5a5a5a) Zusammen ergibt sich für den Punkt
Zusammen ergibt sich für den Punkt  .
.
 Sprungweite bestimmen
Du sollst mit einem Kurvenlängenintegral die Sprungweite des Springers bestimmen. Dazu verwendest du:
Sprungweite bestimmen
Du sollst mit einem Kurvenlängenintegral die Sprungweite des Springers bestimmen. Dazu verwendest du:
![\(l=\int\limits_a^b\sqrt{1+\left[h‘(x)\right]^2}\;\mathrm{d}x\)](https://mathjax.schullv.de/c98a49cefca78e5734487ae016f41f37b89570bef9af1a9c54ea43beebb70411?color=5a5a5a) Der Springer ist von
Der Springer ist von  bis zu einer
bis zu einer  -Koordinate von
-Koordinate von  gesprungen. Mit diesen Integralgrenzen ergibt sich:
gesprungen. Mit diesen Integralgrenzen ergibt sich:
![\(\begin{array}[t]{rll}
l&=& \int\limits_{0}^{114,6}\sqrt{1+\left[h‘(x)\right]^2}\;\mathrm{d}x \\[5pt]
&\approx& 132,44
\end{array}\)](https://mathjax.schullv.de/b6d30d66bf6c72fb4cb1eb42064f904a77845253c4c34f5cbb878e755d7b41df?color=5a5a5a) Sprungweiten werden immer auf halbe Meter auf- bzw. abgerundet, somit ist der Springer
Sprungweiten werden immer auf halbe Meter auf- bzw. abgerundet, somit ist der Springer  m gesprungen.
m gesprungen.
 Koordinaten von
Koordinaten von  bestimmen
Du sollst die Koordinaten von
bestimmen
Du sollst die Koordinaten von  bestimmen.
bestimmen.  liegt so auf
liegt so auf  , dass die Kurvenlänge
, dass die Kurvenlänge  m beträgt. Du erhältst eine Gleichung mit variabler oberer Integralgrenze, welche du erneut mit dem solve Befehl löst:
m beträgt. Du erhältst eine Gleichung mit variabler oberer Integralgrenze, welche du erneut mit dem solve Befehl löst:
![\(\begin{array}[t]{rll}
120&=& \int\limits_0^x\sqrt{1+\left[h‘(t)\right]^2}\;\mathrm{d}t \\[5pt]
x&\approx& 104,16
\end{array}\)](https://mathjax.schullv.de/7158566ff38cf460db996944cc7627716af8b66bda7d0a9743ffcee1dea37041?color=5a5a5a) Die
Die  -Koordinate von
-Koordinate von  ist
ist  . Die
. Die  -Koordinate erhältst du mit
-Koordinate erhältst du mit  .
.
![\(\begin{array}[t]{rll}
h(104,2) &\approx & -59,9 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3241a378a0264040bea01c2d927e978b866310f560e1246b76bf4e98ecb6a321?color=5a5a5a) Zusammen lässt sich
Zusammen lässt sich  schreiben mit
schreiben mit  .
.
 Weitenpunkte bestimmen
Du sollst die Punktzahl
Weitenpunkte bestimmen
Du sollst die Punktzahl  für einen Sprung mit einer Sprungweite von
für einen Sprung mit einer Sprungweite von  m bestimmen. Aus der Tabelle entnimmst du alle relevanten Punktzahlen. Es ist zu beachten, dass ein Springer Punkte nur für Weiten über
m bestimmen. Aus der Tabelle entnimmst du alle relevanten Punktzahlen. Es ist zu beachten, dass ein Springer Punkte nur für Weiten über  m erhält. Da die K-Punkt-Weite
m erhält. Da die K-Punkt-Weite  m beträgt, erhält ein Springer
m beträgt, erhält ein Springer  Punkte für jeden halben Meter zusätzlich zu den
Punkte für jeden halben Meter zusätzlich zu den  Punkte für einen Sprung zum K-Punkt:
Punkte für einen Sprung zum K-Punkt:
![\(\begin{array}[t]{rll}
p&=& (132,5-120)\cdot 2\cdot 0,9+60 \\[5pt]
&=& 82,5
\end{array}\)](https://mathjax.schullv.de/eafcc6b69f6e5ee94dade92cf965997cf2a807459a59612a27c7c8553d4f1b40?color=5a5a5a) Der Springer erhält
Der Springer erhält  Punkte.
Punkte.
 Auftreffwinkel berechnen
Du sollst den Landewinkel des Springers berechnen, welcher dem Winkel zwischen den Graphen von
Auftreffwinkel berechnen
Du sollst den Landewinkel des Springers berechnen, welcher dem Winkel zwischen den Graphen von  und
und  in
in  entspricht. Du kannst erneut den Winkelsatz auf beide Graphen anwenden und die Differenz der Winkel betrachten oder du verwendest die transformierte Formel aus einer Formelsammlung.
entspricht. Du kannst erneut den Winkelsatz auf beide Graphen anwenden und die Differenz der Winkel betrachten oder du verwendest die transformierte Formel aus einer Formelsammlung.
 Lösungsweg A: Differenz der Winkel
Du verwendest für beide Graphen den Winkelsatz und bestimmst so deren Neigung zu einer Horizontalen:
Lösungsweg A: Differenz der Winkel
Du verwendest für beide Graphen den Winkelsatz und bestimmst so deren Neigung zu einer Horizontalen:
![\(\begin{array}[t]{rll}
\tan\varphi&=& h‘(114,6) &\quad \scriptsize \mid\; \arctan \\[5pt]
\varphi&=& \arctan (h‘(114,6)) \\[5pt]
&\approx & -31,68^\circ
\end{array}\)](https://mathjax.schullv.de/01984a11743b000b43f7777afeb9be5758170a8790a267a2020f7340acc3320e?color=5a5a5a)
![\(\begin{array}[t]{rll}
\tan\theta&=& s‘(114,6) &\quad \scriptsize \mid\; \arctan \\[5pt]
\theta&=& \arctan (s‘(114,6)) \\[5pt]
&\approx & -46,74^\circ
\end{array}\)](https://mathjax.schullv.de/50127cc62aee0a3f074765d490c34194e4c639edd26806eb16447ca2bf8419fc?color=5a5a5a) Der Unterschied entspricht dem Landewinkel
Der Unterschied entspricht dem Landewinkel  :
:
![\(\begin{array}[t]{rll}
\gamma&=& -46,74^\circ-(-31,68^\circ) \\[5pt]
&=& -15,06^\circ
\end{array}\)](https://mathjax.schullv.de/5e05e14715bc030dc44e893b3f2821afeac2573ca59a21162603ae2a7598fc25?color=5a5a5a) Der Springer landet mit einem Winkel von
Der Springer landet mit einem Winkel von  .
.
 Lösungsweg B: Angepasste Formel
Verwendest du den Angepassten Winkelsatz ergitb sich:
Lösungsweg B: Angepasste Formel
Verwendest du den Angepassten Winkelsatz ergitb sich:
![\(\begin{array}[t]{rll}
\tan\gamma&=& \frac{s‘(114,6)-h‘(114,6)}{1+s‘(114,6)\cdot h‘(114,6)} &\quad \scriptsize \mid\; \arctan \\[5pt]
\gamma&\approx& \arctan (-0,27) \\[5pt]
&\approx& 15,11^\circ
\end{array}\)](https://mathjax.schullv.de/afc5de0e905b96783ef900120ac34dc67d9b22bea40043ca271c32c4fac33f25?color=5a5a5a) Der Springer landet mit einem Winkel von
Der Springer landet mit einem Winkel von  .
.
 Sachzusammenhang formulieren
Du sollst den Sachzusammenhang zu einem Gleichungssystem formulieren. Du betrachtest dazu die drei Gleichungen getrennt.
1. Schritt:
Sachzusammenhang formulieren
Du sollst den Sachzusammenhang zu einem Gleichungssystem formulieren. Du betrachtest dazu die drei Gleichungen getrennt.
1. Schritt: 
 beschreibt den Abstand des Springers zum Hang als Funktion seiner Entfernung zum Absprungpunkt.
2. Schritt:
beschreibt den Abstand des Springers zum Hang als Funktion seiner Entfernung zum Absprungpunkt.
2. Schritt:  Die Ableitung von
Die Ableitung von  wird
wird  gesetzt. Die Funktion
gesetzt. Die Funktion  also auf Extremstellen untersucht. Es ergebn sich die Stellen
also auf Extremstellen untersucht. Es ergebn sich die Stellen  und
und  .
3. Schritt:
.
3. Schritt:  und
und  Abschließend werden die Funktionswerte an den Extremstellen berechnet. An der Stelle
Abschließend werden die Funktionswerte an den Extremstellen berechnet. An der Stelle  beträgt dieser etwa
beträgt dieser etwa  m. Der gesuchte Wert entspricht dem Maximalen Abstand des Springers zum Hang. Eine Untersuchung auf die Art des Extrempunktes ist nicht nötig, da dieser offenkundig ein Hochpunkt sein muss, da
m. Der gesuchte Wert entspricht dem Maximalen Abstand des Springers zum Hang. Eine Untersuchung auf die Art des Extrempunktes ist nicht nötig, da dieser offenkundig ein Hochpunkt sein muss, da  gelten muss und es nur zwei Extremstellen gibt.
gelten muss und es nur zwei Extremstellen gibt.
 Zweite Flugbahn analysieren
Du sollst Aussagen zu einer zweiten Flugbahn treffen. Dir sind drei Bedingungen gegeben:
Zweite Flugbahn analysieren
Du sollst Aussagen zu einer zweiten Flugbahn treffen. Dir sind drei Bedingungen gegeben:
 , während der erste Springer weiter bis zu
, während der erste Springer weiter bis zu  springt.
2. Schritt: Absprungwinkel entscheiden
Mit dem Winkelsatz berechnest du erneut, diesmal für beide Springer, die Winkel zur Horizontalen:
Aufgabengruppe 2
springt.
2. Schritt: Absprungwinkel entscheiden
Mit dem Winkelsatz berechnest du erneut, diesmal für beide Springer, die Winkel zur Horizontalen:
Aufgabengruppe 2
 Definitions- und Wertebereich sowie Asymptoten angeben
Du sollst Definitionsbereich
Definitions- und Wertebereich sowie Asymptoten angeben
Du sollst Definitionsbereich  , Wertebereich
, Wertebereich  und die Asymptoten der Funktion
und die Asymptoten der Funktion  angeben.
1. Schritt: Definitionsbereich
angeben.
1. Schritt: Definitionsbereich  Die Definitionsmenge
Die Definitionsmenge  einer gebrochen rationalen Funktion ergitb sich aus dem Nenner. Ausgehend von
einer gebrochen rationalen Funktion ergitb sich aus dem Nenner. Ausgehend von  müssen alle Definitionslücken entfernt werden.
Eine Definitionslücke liegt vor, wenn der Nenner
müssen alle Definitionslücken entfernt werden.
Eine Definitionslücke liegt vor, wenn der Nenner  ergibt.
ergibt.
![\(\begin{array}[t]{rll}
0&=& x+3 &\quad \scriptsize \mid\; -3\\[5pt]
x&=& -3
\end{array}\)](https://mathjax.schullv.de/61b1929f1edeabbb659431428fa347bbff16dc60b125994f5d93452cb28c394b?color=5a5a5a)
 ist die einzige Definitionslücke. Somit ist die Definitionsmenge
ist die einzige Definitionslücke. Somit ist die Definitionsmenge  .
2. Schritt: Wertebereich
.
2. Schritt: Wertebereich  Als nächstes bestimmst du den Wertebereich, dazu betrachtest du
Als nächstes bestimmst du den Wertebereich, dazu betrachtest du  und
und  .
.
![\(\begin{array}[t]{rll}
\lim\limits_{x\nearrow -3} f(x)&=+\infty& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0657ae8117a1c2e2b4f982866e028294c1b43f395c8487bed014adfccb18a1e9?color=5a5a5a)
![\(\begin{array}[t]{rll}
\lim\limits_{x\searrow -3} f(x)&=& -\infty \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6ef570d980cd12f5a40fe2f57f1c3ab234c702f6d68e7327a994d9358cdeb075?color=5a5a5a) Somit nimmt
Somit nimmt  alle möglichen Werte an und es gilt
alle möglichen Werte an und es gilt  .
3. Schritt: Asymptoten angeben
Eine senkrechte Asymptote hast du bereits mit der Definitionslücke bestimmt. Es gilt
.
3. Schritt: Asymptoten angeben
Eine senkrechte Asymptote hast du bereits mit der Definitionslücke bestimmt. Es gilt  .
Für die waagerechte Asympotet betrachtest du den Grenzwert
.
Für die waagerechte Asympotet betrachtest du den Grenzwert  :
:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to\pm\infty} f(x)&=& 1 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d4b0ba11a074063d96095abf2db2e857e3071a290f78ac6f93309ad2c0749d47?color=5a5a5a) Zusammen existieren die beiden Asympoten
Zusammen existieren die beiden Asympoten  und
und  .
.
 Gleichung angeben
Du sollst eine Gleichung für eine Funktion
Gleichung angeben
Du sollst eine Gleichung für eine Funktion  angeben, deren Graphen durch Verschiebung aus
angeben, deren Graphen durch Verschiebung aus  entsteht und welcher punktsymmetrisch zum Ursprung ist.
Durch eine Verschiebung um drei nach rechts ergibt sich ein Graph mit der Funktion
entsteht und welcher punktsymmetrisch zum Ursprung ist.
Durch eine Verschiebung um drei nach rechts ergibt sich ein Graph mit der Funktion  . Dieser ist punktsymmetrisch zu
. Dieser ist punktsymmetrisch zu  . Damit er dies zum Urspung ist wird er desweiteren um eins nach unten Verschoben es ergibt sich der Graph
. Damit er dies zum Urspung ist wird er desweiteren um eins nach unten Verschoben es ergibt sich der Graph  .
.
 Umkehrfunktion beschreiben
Du sollst beschreiben, wie man aus der Funktionsvorschrift von
Umkehrfunktion beschreiben
Du sollst beschreiben, wie man aus der Funktionsvorschrift von  die Umkehrfunktion bestimmen kann. Der Graph der Umkehrfunktion entsteht aus der Spiegelung an der ersten Winkelhalbierenden. Dies entspricht einem Vertauschen von
die Umkehrfunktion bestimmen kann. Der Graph der Umkehrfunktion entsteht aus der Spiegelung an der ersten Winkelhalbierenden. Dies entspricht einem Vertauschen von  und
und  .
Die Funktionsvorschrift wird also aus dem Vertauschen von
.
Die Funktionsvorschrift wird also aus dem Vertauschen von  und
und  und Auflösen nach
und Auflösen nach  bestimmt. Da die Umkehrfunktion aus der Vertauschen von
bestimmt. Da die Umkehrfunktion aus der Vertauschen von  und
und  entsteht, tauschen sich auch Werte- und Definitionsbereich, sodass
entsteht, tauschen sich auch Werte- und Definitionsbereich, sodass  und
und  gilt.
gilt.
 Winkel im Koordinatenursprung berechnen
Da die Inverse der Gespiegelten an der ersten Winkelhalbierenden entspricht, ist der Schnittwinkel das Doppelte des Winkels zwischen der Funktion und der Winkelhalbierenden, welche du mit dem Winkelsatz berechnen kannst:
Winkel im Koordinatenursprung berechnen
Da die Inverse der Gespiegelten an der ersten Winkelhalbierenden entspricht, ist der Schnittwinkel das Doppelte des Winkels zwischen der Funktion und der Winkelhalbierenden, welche du mit dem Winkelsatz berechnen kannst:
 Du benötigst die Ableitung von
Du benötigst die Ableitung von  , welche du mit folgendem Befehl berechnest:
, welche du mit folgendem Befehl berechnest:
 Abb. 4: Ableitung bestimmen
Mit dem Winkelsatz berechnest du den Winkel der Funktion zur
Abb. 4: Ableitung bestimmen
Mit dem Winkelsatz berechnest du den Winkel der Funktion zur  -Achse. Der Winkel der Winkelhalbierenden beträgt
-Achse. Der Winkel der Winkelhalbierenden beträgt  .
.
![\(\begin{array}[t]{rll}
\tan\varphi&=& f‘(0) &\quad \scriptsize \mid\; \arctan \\[5pt]
\varphi&=& \arctan (f‘(0)) \\[5pt]
&\approx & 18,43^\circ
\end{array}\)](https://mathjax.schullv.de/51339e9e081a8c72f8bf05a5ef67ed8850b1513705bd543aac8bdfc0332ffafc?color=5a5a5a) Der Winkel der Funktion zur
Der Winkel der Funktion zur  -Achse beträgt
-Achse beträgt  . Somit beträgt der Winkel
. Somit beträgt der Winkel  zwischen Funktion und Umkehrfunktion:
zwischen Funktion und Umkehrfunktion:
![\(\begin{array}[t]{rll}
\theta&=& 2\cdot (45^\circ-18,43^\circ) \\[5pt]
&=& 53,14^\circ
\end{array}\)](https://mathjax.schullv.de/3540e0f73103113f78f5cbe0a4da5f4aefab7cf4795cb82490d903d5ac1683a3?color=5a5a5a)
 schneidet
schneidet  in einem Winkel von
in einem Winkel von  .
.
 Seitenlänge bestimmen
Du sollst einen Seitenlänge des Rechtecks bestimmen, welches durch
Seitenlänge bestimmen
Du sollst einen Seitenlänge des Rechtecks bestimmen, welches durch  halbiert wird. Du suchst also eine Grenze für die Integrale, welchen den Flächeninhalt passend beschreiben. Verwende hierzu das Integral zwischen der Gerade
halbiert wird. Du suchst also eine Grenze für die Integrale, welchen den Flächeninhalt passend beschreiben. Verwende hierzu das Integral zwischen der Gerade  und
und  sowie das Integral für Flächen unterhalb einer Funktion.
Es ergibt sich die Gleichung:
sowie das Integral für Flächen unterhalb einer Funktion.
Es ergibt sich die Gleichung:
![\(\begin{array}[t]{rll}
\int\limits_0^a 1-f(x)\;\mathrm{d}x&=& \int\limits_0^a f(x)\;\mathrm{d}x \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f8ff2a7542ea3d0057f23e6530ea48d78ec8854879b7cd7dd996ce71c4295603?color=5a5a5a) Dieses Integral löst du mit dem solve Befehl:
Dieses Integral löst du mit dem solve Befehl:
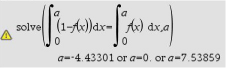 Abb. 5: Gleichung lösen mit dem nspire
Du erhältst drei Lösungen, wobei allerdings nur
Abb. 5: Gleichung lösen mit dem nspire
Du erhältst drei Lösungen, wobei allerdings nur  Sinn im Rahmen der Aufgabenstellung ergibt.
Sinn im Rahmen der Aufgabenstellung ergibt.
 Minimum begründen
Du sollst begründen, dass jede Funktion
Minimum begründen
Du sollst begründen, dass jede Funktion  für
für  ein Minimum besitzt, ohne dass du dabei die Ableitung verwendest. Betrachte dazu am besten die Nullstellenbedingung einer gebrochen rationalen Funktion.
Eine gebrochen rationale Funktion ist nur genau dann
ein Minimum besitzt, ohne dass du dabei die Ableitung verwendest. Betrachte dazu am besten die Nullstellenbedingung einer gebrochen rationalen Funktion.
Eine gebrochen rationale Funktion ist nur genau dann  wenn der Zähler
wenn der Zähler  ist. Im Falle von
ist. Im Falle von  also nur für
also nur für  . Da es sich bei
. Da es sich bei  um eine nach oben geöffnete Normalparabel handelt, liegt für
um eine nach oben geöffnete Normalparabel handelt, liegt für  ein Minimum vor. Diese Argumentation ist unabhängig von
ein Minimum vor. Diese Argumentation ist unabhängig von  und da
und da  ist, ist der Nenner immer positiv. Somit liegt für alle
ist, ist der Nenner immer positiv. Somit liegt für alle  bei
bei  ein Minimum vor.
ein Minimum vor.
 Wendepunkte auf Parallele zur
Wendepunkte auf Parallele zur  -Achse nachweisen
Du sollst nachweisen, dass alle Wendepunkte von
-Achse nachweisen
Du sollst nachweisen, dass alle Wendepunkte von  auf einer Parallelen zur
auf einer Parallelen zur  -Achsen liegen. Für Wendepunkte gilt, dass die zweite Ableitung einer Funktion
-Achsen liegen. Für Wendepunkte gilt, dass die zweite Ableitung einer Funktion  ist. Die Ableitung berechnest du erneut mit dem diff Befehl:
ist. Die Ableitung berechnest du erneut mit dem diff Befehl:
![\(\begin{array}[t]{rll}
f_k‘(x)&=& \frac{2\cdot k^2\cdot x}{(x^2+k^2)^2} \\[10pt]
f_k‘‘(x)&=& \frac{2\cdot k^4-6\cdot k^2\cdot x^2}{(x^2+k^2)^3} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/b27cc03fc690aa0ef50a696d62eb5280263cb83e3ed347fc0e67566e61776d3e?color=5a5a5a) Um auf die Nullstellen zu schließen, ist lediglich der Zähler zu betrachten.
Dies sind alle Wendepunkt des Graphen von
Um auf die Nullstellen zu schließen, ist lediglich der Zähler zu betrachten.
Dies sind alle Wendepunkt des Graphen von  . Um nachzuweisen, dass sie auf einer Parallelen zu
. Um nachzuweisen, dass sie auf einer Parallelen zu  -Achse liegen, berechnest du die
-Achse liegen, berechnest du die  -Koordinaten.
-Koordinaten.
![\(\begin{array}[t]{rll}
f_k\left(\pm\sqrt{\frac{1}{3}}\cdot k\right)&=& \frac{1}{4} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6713f1c1790fa63913de513c0a69daaef1a9a7e9474e0c6dea3b7d448312e377?color=5a5a5a) Beide Wendepunkt vom Graphen von
Beide Wendepunkt vom Graphen von  liegen auf der Parallelen zur
liegen auf der Parallelen zur  -Achse mit
-Achse mit  . Da dieser Wert nicht von
. Da dieser Wert nicht von  abhängt, liegen alle Wendepunkt der möglichen Funktionen der Schar auf dieser Parallelen.
abhängt, liegen alle Wendepunkt der möglichen Funktionen der Schar auf dieser Parallelen.
 Flächeninhalt berechnen und maximieren
Du sollst, für
Flächeninhalt berechnen und maximieren
Du sollst, für  , den Flächeninhalt des Dreiecks
, den Flächeninhalt des Dreiecks  zwischen den Punkten
zwischen den Punkten  ,
,  und
und  berechnen. Da es sich hierbei nicht um ein Recktwinkliges Dreieck handelt, da
berechnen. Da es sich hierbei nicht um ein Recktwinkliges Dreieck handelt, da  und
und  nicht die selbe
nicht die selbe  -Koordinate aufweisen, behilfst du dir über ein weiteres Dreieck
-Koordinate aufweisen, behilfst du dir über ein weiteres Dreieck  zwischen den Punkten
zwischen den Punkten  ,
,  und
und  .
Von diesem kannst du den Flächeninhalt normal berechnen.
.
Von diesem kannst du den Flächeninhalt normal berechnen.
![\(\begin{array}[t]{rll}
A_{p‘}&=& \frac{1}{2}\cdot p\cdot f_4(p) \\[5pt]
&=& \frac{1}{2}\cdot p\cdot\frac{p^2}{p^2+16} \\[5pt]
&=& \frac{p^3}{2\cdot (p^2+16)}
\end{array}\)](https://mathjax.schullv.de/dab0a5eee31da01e71ea89dc3a9f3dd119c43d1c4431201e3a70e6eb01494814?color=5a5a5a) Dabei ist
Dabei ist  um das Dreieck zwischen
um das Dreieck zwischen  ,
,  und
und  größer.
größer.
![\(\begin{array}[t]{rll}
A_p&=& A_{p‘}-\frac{1}{2}\cdot p\cdot 1 \\[5pt]
&=& \frac{p^3}{2\cdot (p^2+16)}-\frac{p}{2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/574842cf73f027b3e8951a6c39f3036fbd99bcd61e2b3658123b0c5a0ac2179f?color=5a5a5a) Diesen Ausdruck vereinfachst du im Ausgabefenster.
Diesen Ausdruck vereinfachst du im Ausgabefenster.
 Abb. 6: Ausdruck vereinfachen
Flächeninhalte an sich sind positiv, deshalb betrachtest du den Betrag.
Abb. 6: Ausdruck vereinfachen
Flächeninhalte an sich sind positiv, deshalb betrachtest du den Betrag.
![\(\begin{array}[t]{rll}
A_p&=& \frac{8\cdot p}{p^2+16} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3ad580839a903ee9ef47af477e961f2e2392288d5430388b5b49704e7511ab31?color=5a5a5a) Abschließend sollst du den maximalen Flächeninhalt oder eben das Maximum von
Abschließend sollst du den maximalen Flächeninhalt oder eben das Maximum von  bestimmen. Diesen bestimmst du mit dem Befehl fMax:
bestimmen. Diesen bestimmst du mit dem Befehl fMax:
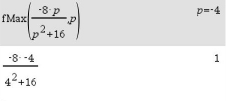 Abb. 7: Maximum bestimmen
Das Maximum der Dreiecksfläceh beträgt
Abb. 7: Maximum bestimmen
Das Maximum der Dreiecksfläceh beträgt  an der Stelle
an der Stelle  .
.
 Graph zeichnen
Du sollst den Graphen der Funktion
Graph zeichnen
Du sollst den Graphen der Funktion  im Intervall
im Intervall ![\(\left[-25 \, ; \, 175\right]\)](https://mathjax.schullv.de/55348b4038f774c4652f8ec09c0f618aafffdbc75568c39b442464d7810064bd?color=5a5a5a) zeichnen.
Bei der Funktion handelt es sich um einen gestreckte Sinus. Bestimme mit dem TR die kritischen Punkte im betrachteten Intervall.
zeichnen.
Bei der Funktion handelt es sich um einen gestreckte Sinus. Bestimme mit dem TR die kritischen Punkte im betrachteten Intervall.
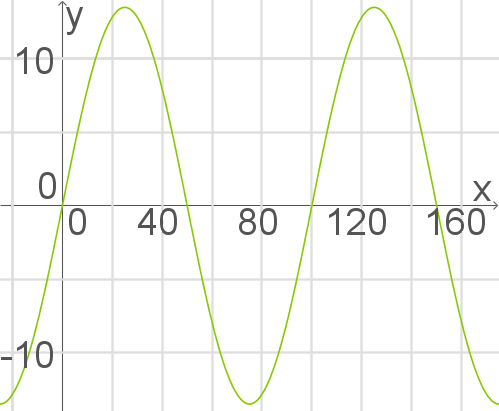 Abb. 8: Graph zeichnen
Abb. 8: Graph zeichnen
 Schrittweise Umwandlung einer
Schrittweise Umwandlung einer  -Funktion
Du sollst angeben wie der Graph von
-Funktion
Du sollst angeben wie der Graph von  aus dem Graphen einer normalen Sinus-Funktion hervorgeht.
Dies geschieht in zwei Schritten. Zuerst wird die Periode mit dem Faktor
aus dem Graphen einer normalen Sinus-Funktion hervorgeht.
Dies geschieht in zwei Schritten. Zuerst wird die Periode mit dem Faktor  angepasst. Dies entspricht einer Streckung entlang der
angepasst. Dies entspricht einer Streckung entlang der  -Achse.
Danach wird der Graph entlang der
-Achse.
Danach wird der Graph entlang der  -Achse gestreckt. Die Amplitude wird auf
-Achse gestreckt. Die Amplitude wird auf  erhöht.
erhöht.
 Mittlere Dicke bestimmen
Du sollst unter Verwendung der Kurvenlänge und der Konitnuität des Volumens die mittlere Dicke des Blechs nach der Umformung zu Wellblech bestimmen. Betrachte hierzu die Ausgangssituation.
1. Schritt: Volumen bestimmen
Zu Beginn ist das Blech quadratisch, einen Meter lang und zwei Milimeter bzw.
Mittlere Dicke bestimmen
Du sollst unter Verwendung der Kurvenlänge und der Konitnuität des Volumens die mittlere Dicke des Blechs nach der Umformung zu Wellblech bestimmen. Betrachte hierzu die Ausgangssituation.
1. Schritt: Volumen bestimmen
Zu Beginn ist das Blech quadratisch, einen Meter lang und zwei Milimeter bzw.  m dick. Für das Volumen
m dick. Für das Volumen  gilt:
gilt:
![\(\begin{array}[t]{rll}
V&=& 1\cdot 1\cdot 0,002 \\[5pt]
&=& 0,002
\end{array}\)](https://mathjax.schullv.de/d149af8caccc6a010652115f61b482571ed8a037cbee96a6749b42232e89da19?color=5a5a5a) Vor der Umformung beträgt des Volumen
Vor der Umformung beträgt des Volumen  m
m .
2. Schritt: Kurvenlänge bestimmen
Mit der angegebenen Formel bestimmst du die Kurvenlänge
.
2. Schritt: Kurvenlänge bestimmen
Mit der angegebenen Formel bestimmst du die Kurvenlänge  zwischen den beiden Grenzen
zwischen den beiden Grenzen  und
und  , da
, da  mm einem Meter entsprechen.
Die Ableitung von
mm einem Meter entsprechen.
Die Ableitung von  bestimmst du erneut mit dem diff Befehl.
bestimmst du erneut mit dem diff Befehl.
![\(\begin{array}[t]{rll}
l&=& \int\limits_0^{1.000} \sqrt{1+\left[ w‘(x) \right]^2}\;\mathrm{d}x \\[5pt]
&\approx& 1.219,56
\end{array}\)](https://mathjax.schullv.de/b9bda0acc33c5833cd6b13c7a1b37cd5326012593f0b635a8ce9a6a8e8a14e5f?color=5a5a5a) Die Länge des Wellblechs beträgt
Die Länge des Wellblechs beträgt  mm
mm m.
3. Schritt: Dicke bestimmen
Mit dieser Angabe kannst du aus dem Volumen des ersten Schrittes die Dicke des Wellblechs bestimmen.
m.
3. Schritt: Dicke bestimmen
Mit dieser Angabe kannst du aus dem Volumen des ersten Schrittes die Dicke des Wellblechs bestimmen.
![\(\begin{array}[t]{rll}
V&=& 0,002& \\[5pt]
0,002 &=& 1\cdot 1,21956\cdot d \\[5pt]
d&\approx& 0,00164
\end{array}\)](https://mathjax.schullv.de/eb487451a81829bcd22a2e5bd9aee078dbccadc98d5346b842c7b642faf71146?color=5a5a5a) Die Dicke beträgt
Die Dicke beträgt  mm.
mm.
 Volumen des Hohlraums bestimmen
Du sollst das Volumen bestimmen, welches mit Bauschaum aufgefüllt werden muss. Nimmst du die ebene Dachfläche als
Volumen des Hohlraums bestimmen
Du sollst das Volumen bestimmen, welches mit Bauschaum aufgefüllt werden muss. Nimmst du die ebene Dachfläche als  -Achse an, verändert sich die Funktion
-Achse an, verändert sich die Funktion  , da der Graph nach oben verschoben werden muss, damit seine Tiefpunkte auf der Achse liegen. Nenne die neue Funktion
, da der Graph nach oben verschoben werden muss, damit seine Tiefpunkte auf der Achse liegen. Nenne die neue Funktion  .
.
![\(\begin{array}[t]{rll}
W(x)&=& w(x)+13,5 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b4f5ac8253315bec75238faebcf351a0a6c7a00719e5ebad48bbcfedd1922b80?color=5a5a5a) Für das Volumen des Bauschaums bestimmst du zuerst die Größe der Querschnittsfläche respektive das Integral über
Für das Volumen des Bauschaums bestimmst du zuerst die Größe der Querschnittsfläche respektive das Integral über  .
.
![\(\begin{array}[t]{rll}
A&=& \int\limits_{0}^{1000} W(x)\;\mathrm{d}x \\[5pt]
&\approx& 20.189,5
\end{array}\)](https://mathjax.schullv.de/53e69daf4d17a471acb8434eb5828872e9a3c26bc9fa01e3e3462c6963bee067?color=5a5a5a) Mit dieser Querschnittsfläche kannst du das benötigte Volumen des Bauschaums berechnen.
Mit dieser Querschnittsfläche kannst du das benötigte Volumen des Bauschaums berechnen.
![\(\begin{array}[t]{rll}
V&=& 0,0201895\cdot 1 \\[5pt]
&\approx& 0,02
\end{array}\)](https://mathjax.schullv.de/fee11122bd8c78e4be294f977a6efaa4fd9fb3bdb5029cd1bedc544541193882?color=5a5a5a) Es werden
Es werden  m
m Schaum benötigt.
Schaum benötigt.
1)
a)
b)
Menu  Algebra
Algebra  Gleichungssystem lösen
Gleichungssystem lösen  Gleichungssystem lösen
Gleichungssystem lösen
 Abb. 1: Gleichungssystem lösen mit dem nspire
Abb. 1: Gleichungssystem lösen mit dem nspire
2)
a)
b)
Menu  Algebra
Algebra  Löse
Löse
 Abb. 2: Gleichung lösen mit dem nspire
Abb. 2: Gleichung lösen mit dem nspire
3)
a)
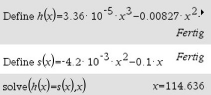 Abb. 3: Gleichung lösen mit dem nspire
Abb. 3: Gleichung lösen mit dem nspire
b)
c)
d)
e)
f)
g)
: Springer springt am Absprungpunkt ab
: Daraus lässt sich der Winkel im Absprung berechnen
: Der Springer landet bei
Erster Springer
![\(\begin{array}[t]{rll}
\varphi&=& \arctan (s‘(0)) \\[5pt]
&\approx& -5,71^\circ
\end{array}\)](https://mathjax.schullv.de/52008f2a53f830ebfd2603e76bae842a6678b7562940917f31e19330282570f6?color=5a5a5a)
Zweiter Springer
![\(\begin{array}[t]{rll}
\theta&=& \arctan (t‘(0) ) \\[5pt]
&\approx& -4,97^\circ
\end{array}\)](https://mathjax.schullv.de/cd41e44529b37456119ee5a9c338a80ec6c02c085070506e4b6e9a7d3fcead20?color=5a5a5a)
Ebenfalls der erste Springer springt unter dem größeren Winkel ab.
1)
a)
b)
c)
d)
Menu  Analysis
Analysis  Ableitung
Ableitung
 Abb. 4: Ableitung bestimmen
Abb. 4: Ableitung bestimmen
e)
Menu  Algebra
Algebra  Löse
Löse
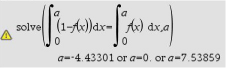 Abb. 5: Gleichung lösen mit dem nspire
Abb. 5: Gleichung lösen mit dem nspire
2)
a)
b)
c)
 Abb. 6: Ausdruck vereinfachen
Abb. 6: Ausdruck vereinfachen
Menu  Analysis
Analysis  fMax
fMax
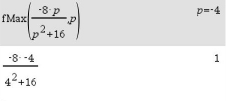 Abb. 7: Maximum bestimmen
Abb. 7: Maximum bestimmen
3)
a)
 Abb. 8: Graph zeichnen
Abb. 8: Graph zeichnen
b)
c)
d)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabengruppe 1
 Geradengleichung bestimmen
Du sollst die Gleichung einer Geraden durch die Punkte
Geradengleichung bestimmen
Du sollst die Gleichung einer Geraden durch die Punkte  und
und  bestimmen. Das Problem hierbei liegt darin, dass dir die Koordinaten des Punktes
bestimmen. Das Problem hierbei liegt darin, dass dir die Koordinaten des Punktes  nicht bekannt sind. Allerdings kannst du mit dem angegebenen Winkel von
nicht bekannt sind. Allerdings kannst du mit dem angegebenen Winkel von  und dem Winkelsatz
und dem Winkelsatz  auf die Steigung der Geraden schließen.
auf die Steigung der Geraden schließen.
![\(\begin{array}[t]{rll}
m&=& \tan( -35^\circ) \\[5pt]
&\approx& -0,7
\end{array}\)](https://mathjax.schullv.de/c76a37d9b004464a37828512012a6e2b8b5e71f2e78d3ad0439273235f40b00f?color=5a5a5a) Die Steigung beträgt
Die Steigung beträgt  somit kannst du eine Geradengleichung durch Verschiebung aufstellen.
somit kannst du eine Geradengleichung durch Verschiebung aufstellen.
![\(\begin{array}[t]{rll}
y=&=& -0,7\cdot (x+94)+51\\[5pt]
&=& -0,7\cdot x-14,8
\end{array}\)](https://mathjax.schullv.de/904cb25a78eefcebdbc9f06d1252f092447f59f5aa40a2e1c6d95bc5aa3de509?color=5a5a5a) Diese Grade läuft durch die Punkte
Diese Grade läuft durch die Punkte  und
und  .
.
 Koordinaten von
Koordinaten von  bestimmen
Du sollst die Koordinaten des Punktes
bestimmen
Du sollst die Koordinaten des Punktes  auf eine Nachkommastelle genau bestimmen. Du kennst die Geradengleichung und den Abstand der beiden Punkte. Mit dem Pythagoras kannst du ein Gleichungssystem aufstellen:
auf eine Nachkommastelle genau bestimmen. Du kennst die Geradengleichung und den Abstand der beiden Punkte. Mit dem Pythagoras kannst du ein Gleichungssystem aufstellen:
![\(\begin{array}[t]{rll}
50^2&=& (-94-x)^2+(51-y)^2 \\[5pt]
y&=& -0,7\cdot x-14,8
\end{array}\)](https://mathjax.schullv.de/d89071e6ba7bbb4fc36d956bb1cd67cc3a925461d2451d6a5adee6b539594000?color=5a5a5a) Das Gleichungssystem löst du mit dem Befehl:
Das Gleichungssystem löst du mit dem Befehl:
 Abb. 1: Gleichungssystem lösen mit dem Classpad
Es handelt sich um ein Gleichungssystem mit quadratischen Termen und du erhältst deshalb zwei Lösungen. Da
Abb. 1: Gleichungssystem lösen mit dem Classpad
Es handelt sich um ein Gleichungssystem mit quadratischen Termen und du erhältst deshalb zwei Lösungen. Da  weiter rechts liegt als
weiter rechts liegt als  erhältst du
erhältst du  .
.
 Höhe des Absprungpunktes bestimmen
Du sollst den Höhenunterschied zwischen der Absprungkante und dem Beginn des Aufsprunghangs bestimmen. Die Absprungkante liegt im Koordinatenursprung
Höhe des Absprungpunktes bestimmen
Du sollst den Höhenunterschied zwischen der Absprungkante und dem Beginn des Aufsprunghangs bestimmen. Die Absprungkante liegt im Koordinatenursprung  , der Aufsprunghang beginnt im Punkt
, der Aufsprunghang beginnt im Punkt  .
Das einzige dir Unbekannte ist die
.
Das einzige dir Unbekannte ist die  -Koordinate von
-Koordinate von  , welche du mit
, welche du mit  berechnest:
Der gesuchte Abstand
berechnest:
Der gesuchte Abstand  berechnest du aus der Differenz der
berechnest du aus der Differenz der  -Koordinaten:
-Koordinaten:
![\(\begin{array}[t]{rll}
\Delta &=& 0-h(0)\\[5pt]
&=& 3,38
\end{array}\)](https://mathjax.schullv.de/cf9c8021a03954eedc9087c9e4f005df40dba0f1959d537dc0192ac6bde5cc5e?color=5a5a5a) Der Abstand zwischen Absprungkante und Aufsprunghang beträgt
Der Abstand zwischen Absprungkante und Aufsprunghang beträgt  m.
m.
 Hillsize und Abweichung zum Soll berechnen
Du sollst die Hillsize, das Maß für die Größe einer Skisprunganlage, berechnen. Du weißt, dass die Hillsize die Länge der Strecke zwischen dem Absprungpunkt und dem Hillsize-Punkt, welcher auf
Hillsize und Abweichung zum Soll berechnen
Du sollst die Hillsize, das Maß für die Größe einer Skisprunganlage, berechnen. Du weißt, dass die Hillsize die Länge der Strecke zwischen dem Absprungpunkt und dem Hillsize-Punkt, welcher auf  liegt, ist. Zuerst bestimmst du dementsprechend die Koordinaten des Hillsize-Punktes, dessen Steigung
liegt, ist. Zuerst bestimmst du dementsprechend die Koordinaten des Hillsize-Punktes, dessen Steigung  beträgt. Dazu verwendest du den Winkelsatz:
beträgt. Dazu verwendest du den Winkelsatz:
 1. Schritt: Stelle des Hillsize-Punktes bestimmen
Du suchst die Stelle
1. Schritt: Stelle des Hillsize-Punktes bestimmen
Du suchst die Stelle  für welche gilt:
für welche gilt:
![\(\begin{array}[t]{rll}
h‘(x_H)&=& \tan(-32^\circ) \\[5pt]
\end{array}\)](https://mathjax.schullv.de/5a2da93ca7fc8551f380be80854d8a5b93e45197bbd52a3539ce75a8900d7aea?color=5a5a5a) Diese Gleichung löst du mit:
Diese Gleichung löst du mit:
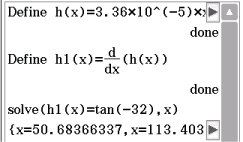 Abb. 2: Gleichung lösen mit dem Classpad
Du erhältst erneut zwei Lösungen, wobei du nur
Abb. 2: Gleichung lösen mit dem Classpad
Du erhältst erneut zwei Lösungen, wobei du nur  beachtest.
2. Schritt: Hillsize-Punkt bestimmen
Aus der
beachtest.
2. Schritt: Hillsize-Punkt bestimmen
Aus der  -Koordinate bestimmst du den Hillsizepunkt
-Koordinate bestimmst du den Hillsizepunkt  .
Für
.
Für  ergeben sich die Koordinaten
ergeben sich die Koordinaten  .
3. Schritt: Abstand zum Absprungpunkt bestimmen
Jetzt ist es möglich den Abstand, also die Hillsize
.
3. Schritt: Abstand zum Absprungpunkt bestimmen
Jetzt ist es möglich den Abstand, also die Hillsize  , zum Absprungpunkt
, zum Absprungpunkt  zu bestimmen. Dazu verwendest du den Satz des Pythagoras.
Es ergibt sich eine Hillsize von
zu bestimmen. Dazu verwendest du den Satz des Pythagoras.
Es ergibt sich eine Hillsize von  m.
4. Schritt: Abweichung bestimmen
Du sollst die prozentuale Abweichung
m.
4. Schritt: Abweichung bestimmen
Du sollst die prozentuale Abweichung  zur tatsächlichen Hillsize von
zur tatsächlichen Hillsize von  m bestimmen.
m bestimmen.
![\(\begin{array}[t]{rll}
\delta&=& \frac{131-132}{132} \\[5pt]
&\approx & -7,58\cdot 10^{-3} = -0,758\%
\end{array}\)](https://mathjax.schullv.de/931ec0215de8db741eff62dcb769880fed5b51fd10f71c367a76a8495ae9215d?color=5a5a5a) Die Abweichung zur tatsächlichen Hillsize beträgt weniger
Die Abweichung zur tatsächlichen Hillsize beträgt weniger  .
.
 Koordinaten von
Koordinaten von  bestimmen
Du sollst die Koordinaten des Punktes
bestimmen
Du sollst die Koordinaten des Punktes  bestimmen, welcher den Landepunkt eines Springers mit der Flugbahn
bestimmen, welcher den Landepunkt eines Springers mit der Flugbahn  beschreibt. Du bestimmst somit den Schnittpunkt
beschreibt. Du bestimmst somit den Schnittpunkt  von
von  und
und  . Dazu verwendest du erneut den solve Befehl.
. Dazu verwendest du erneut den solve Befehl.
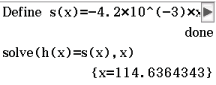 Abb. 3: Gleichung lösen mit dem Classpad
Es ergibt sich
Abb. 3: Gleichung lösen mit dem Classpad
Es ergibt sich  . Als zweites fehlt die
. Als zweites fehlt die  -Koordinate. Dazu kannst du sowohl die Funktion
-Koordinate. Dazu kannst du sowohl die Funktion  als auch
als auch  verwenden.
verwenden.
![\(\begin{array}[t]{rll}
s(114,6)&\approx& -66,6 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/930191f9a974648db4796b20a92d527e219d1d942a529bce0b747b323db9184b?color=5a5a5a) Zusammen ergibt sich für den Punkt
Zusammen ergibt sich für den Punkt  .
.
 Sprungweite bestimmen
Du sollst mit einem Kurvenlängenintegral die Sprungweite des Springers bestimmen. Dazu verwendest du:
Sprungweite bestimmen
Du sollst mit einem Kurvenlängenintegral die Sprungweite des Springers bestimmen. Dazu verwendest du:
![\(l=\int\limits_a^b\sqrt{1+\left[h‘(x)\right]^2}\;\mathrm{d}x\)](https://mathjax.schullv.de/c98a49cefca78e5734487ae016f41f37b89570bef9af1a9c54ea43beebb70411?color=5a5a5a) Der Springer ist von
Der Springer ist von  bis zu einer
bis zu einer  -Koordinate von
-Koordinate von  gesprungen. Mit diesen Integralgrenzen ergibt sich:
gesprungen. Mit diesen Integralgrenzen ergibt sich:
![\(\begin{array}[t]{rll}
l&=& \int\limits_{0}^{114,6}\sqrt{1+\left[h‘(x)\right]^2}\;\mathrm{d}x \\[5pt]
&\approx& 132,44
\end{array}\)](https://mathjax.schullv.de/b6d30d66bf6c72fb4cb1eb42064f904a77845253c4c34f5cbb878e755d7b41df?color=5a5a5a) Sprungweiten werden immer auf halbe Meter auf- bzw. abgerundet, somit ist der Springer
Sprungweiten werden immer auf halbe Meter auf- bzw. abgerundet, somit ist der Springer  m gesprungen.
m gesprungen.
 Koordinaten von
Koordinaten von  bestimmen
Du sollst die Koordinaten von
bestimmen
Du sollst die Koordinaten von  bestimmen.
bestimmen.  liegt so auf
liegt so auf  , dass die Kurvenlänge
, dass die Kurvenlänge  m beträgt. Du erhältst eine Gleichung mit variabler oberer Integralgrenze, welche du erneut mit dem solve Befehl löst:
m beträgt. Du erhältst eine Gleichung mit variabler oberer Integralgrenze, welche du erneut mit dem solve Befehl löst:
![\(\begin{array}[t]{rll}
120&=& \int\limits_0^x\sqrt{1+\left[h‘(t)\right]^2}\;\mathrm{d}t \\[5pt]
x&\approx& 104,16
\end{array}\)](https://mathjax.schullv.de/7158566ff38cf460db996944cc7627716af8b66bda7d0a9743ffcee1dea37041?color=5a5a5a) Die
Die  -Koordinate von
-Koordinate von  ist
ist  . Die
. Die  -Koordinate erhältst du mit
-Koordinate erhältst du mit  .
.
![\(\begin{array}[t]{rll}
h(104,2) &\approx & -59,9 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/46f1584a5f9e506a59b796266ffadfb2c62a058aeb7206c9cb727479bb92c8a2?color=5a5a5a) Zusammen lässt sich
Zusammen lässt sich  schreiben mit
schreiben mit  .
.
 Weitenpunkte bestimmen
Du sollst die Punktzahl
Weitenpunkte bestimmen
Du sollst die Punktzahl  für einen Sprung mit einer Sprungweite von
für einen Sprung mit einer Sprungweite von  m bestimmen. Aus der Tabelle entnimmst du alle relevanten Punktzahlen. Es ist zu beachten, dass ein Springer Punkte nur für Weiten über
m bestimmen. Aus der Tabelle entnimmst du alle relevanten Punktzahlen. Es ist zu beachten, dass ein Springer Punkte nur für Weiten über  m erhält. Da die K-Punkt-Weite
m erhält. Da die K-Punkt-Weite  m beträgt, erhält ein Springer
m beträgt, erhält ein Springer  Punkte für jeden halben Meter zusätzlich zu den
Punkte für jeden halben Meter zusätzlich zu den  Punkte für einen Sprung zum K-Punkt:
Punkte für einen Sprung zum K-Punkt:
![\(\begin{array}[t]{rll}
p&=& (132,5-120)\cdot 2\cdot 0,9+60 \\[5pt]
&=& 82,5
\end{array}\)](https://mathjax.schullv.de/eafcc6b69f6e5ee94dade92cf965997cf2a807459a59612a27c7c8553d4f1b40?color=5a5a5a) Der Springer erhält
Der Springer erhält  Punkte.
Punkte.
 Auftreffwinkel berechnen
Du sollst den Landewinkel des Springers berechnen, welcher dem Winkel zwischen den Graphen von
Auftreffwinkel berechnen
Du sollst den Landewinkel des Springers berechnen, welcher dem Winkel zwischen den Graphen von  und
und  in
in  entspricht. Du kannst erneut den Winkelsatz auf beide Graphen anwenden und die Differenz der Winkel betrachten oder du verwendest die transformierte Formel aus einer Formelsammlung.
entspricht. Du kannst erneut den Winkelsatz auf beide Graphen anwenden und die Differenz der Winkel betrachten oder du verwendest die transformierte Formel aus einer Formelsammlung.
 Lösungsweg A: Differenz der Winkel
Du verwendest für beide Graphen den Winkelsatz und bestimmst so deren Neigung zu einer Horizontalen:
Lösungsweg A: Differenz der Winkel
Du verwendest für beide Graphen den Winkelsatz und bestimmst so deren Neigung zu einer Horizontalen:
![\(\begin{array}[t]{rll}
\tan\varphi&=& h‘(114,6) &\quad \scriptsize \mid\; \arctan \\[5pt]
\varphi&=& \arctan (h‘(114,6)) \\[5pt]
&\approx & -31,68^\circ
\end{array}\)](https://mathjax.schullv.de/01984a11743b000b43f7777afeb9be5758170a8790a267a2020f7340acc3320e?color=5a5a5a)
![\(\begin{array}[t]{rll}
\tan\theta&=& s‘(114,6) &\quad \scriptsize \mid\; \arctan \\[5pt]
\theta&=& \arctan (s‘(114,6)) \\[5pt]
&\approx & -46,74^\circ
\end{array}\)](https://mathjax.schullv.de/50127cc62aee0a3f074765d490c34194e4c639edd26806eb16447ca2bf8419fc?color=5a5a5a) Der Unterschied entspricht dem Landewinkel
Der Unterschied entspricht dem Landewinkel  :
:
![\(\begin{array}[t]{rll}
\gamma&=& -46,74^\circ-(-31,68^\circ) \\[5pt]
&=& -15,06^\circ
\end{array}\)](https://mathjax.schullv.de/de0294187a40873325c08983fef40a3a8636fbcea420b06869a30a815c48a6c8?color=5a5a5a) Der Springer landet mit einem Winkel von
Der Springer landet mit einem Winkel von  .
.
 Lösungsweg B: Angepasste Formel
Verwendest du den Angepassten Winkelsatz ergitb sich:
Lösungsweg B: Angepasste Formel
Verwendest du den Angepassten Winkelsatz ergitb sich:
![\(\begin{array}[t]{rll}
\tan\gamma&=& \frac{s‘(114,6)-h‘(114,6)}{1+s‘(114,6)\cdot h‘(114,6)} &\quad \scriptsize \mid\; \arctan \\[5pt]
\gamma&\approx& \arctan (-0,27) \\[5pt]
&\approx& 15,11^\circ
\end{array}\)](https://mathjax.schullv.de/afc5de0e905b96783ef900120ac34dc67d9b22bea40043ca271c32c4fac33f25?color=5a5a5a) Der Springer landet mit einem Winkel von
Der Springer landet mit einem Winkel von  .
.
 Sachzusammenhang formulieren
Du sollst den Sachzusammenhang zu einem Gleichungssystem formulieren. Du betrachtest dazu die drei Gleichungen getrennt.
1. Schritt:
Sachzusammenhang formulieren
Du sollst den Sachzusammenhang zu einem Gleichungssystem formulieren. Du betrachtest dazu die drei Gleichungen getrennt.
1. Schritt: 
 beschreibt den Abstand des Springers zum Hang als Funktion seiner Entfernung zum Absprungpunkt.
2. Schritt:
beschreibt den Abstand des Springers zum Hang als Funktion seiner Entfernung zum Absprungpunkt.
2. Schritt:  Die Ableitung von
Die Ableitung von  wird
wird  gesetzt. Die Funktion
gesetzt. Die Funktion  also auf Extremstellen untersucht. Es ergebn sich die Stellen
also auf Extremstellen untersucht. Es ergebn sich die Stellen  und
und  .
3. Schritt:
.
3. Schritt:  und
und  Abschließend werden die Funktionswerte an den Extremstellen berechnet. An der Stelle
Abschließend werden die Funktionswerte an den Extremstellen berechnet. An der Stelle  beträgt dieser etwa
beträgt dieser etwa  m. Der gesuchte Wert entspricht dem Maximalen Abstand des Springers zum Hang. Eine Untersuchung auf die Art des Extrempunktes ist nicht nötig, da dieser offenkundig ein Hochpunkt sein muss, da
m. Der gesuchte Wert entspricht dem Maximalen Abstand des Springers zum Hang. Eine Untersuchung auf die Art des Extrempunktes ist nicht nötig, da dieser offenkundig ein Hochpunkt sein muss, da  gelten muss und es nur zwei Extremstellen gibt.
gelten muss und es nur zwei Extremstellen gibt.
 Zweite Flugbahn analysieren
Du sollst Aussagen zu einer zweiten Flugbahn treffen. Dir sind drei Bedingungen gegeben:
Zweite Flugbahn analysieren
Du sollst Aussagen zu einer zweiten Flugbahn treffen. Dir sind drei Bedingungen gegeben:
 , während der erste Springer weiter bis zu
, während der erste Springer weiter bis zu  springt.
2. Schritt: Absprungwinkel entscheiden
Mit dem Winkelsatz berechnest du erneut, diesmal für beide Springer, die Winkel zur Horizontalen:
Aufgabengruppe 2
springt.
2. Schritt: Absprungwinkel entscheiden
Mit dem Winkelsatz berechnest du erneut, diesmal für beide Springer, die Winkel zur Horizontalen:
Aufgabengruppe 2
 Definitions- und Wertebereich sowie Asymptoten angeben
Du sollst Definitionsbereich
Definitions- und Wertebereich sowie Asymptoten angeben
Du sollst Definitionsbereich  , Wertebereich
, Wertebereich  und die Asymptoten der Funktion
und die Asymptoten der Funktion  angeben.
1. Schritt: Definitionsbereich
angeben.
1. Schritt: Definitionsbereich  Die Definitionsmenge
Die Definitionsmenge  einer gebrochen rationalen Funktion ergitb sich aus dem Nenner. Ausgehend von
einer gebrochen rationalen Funktion ergitb sich aus dem Nenner. Ausgehend von  müssen alle Definitionslücken entfernt werden.
Eine Definitionslücke liegt vor, wenn der Nenner
müssen alle Definitionslücken entfernt werden.
Eine Definitionslücke liegt vor, wenn der Nenner  ergibt.
ergibt.
![\(\begin{array}[t]{rll}
0&=& x+3 &\quad \scriptsize \mid\; -3\\[5pt]
x&=& -3
\end{array}\)](https://mathjax.schullv.de/61b1929f1edeabbb659431428fa347bbff16dc60b125994f5d93452cb28c394b?color=5a5a5a)
 ist die einzige Definitionslücke. Somit ist die Definitionsmenge
ist die einzige Definitionslücke. Somit ist die Definitionsmenge  .
2. Schritt: Wertebereich
.
2. Schritt: Wertebereich  Als nächstes bestimmst du den Wertebereich, dazu betrachtest du
Als nächstes bestimmst du den Wertebereich, dazu betrachtest du  und
und  .
.
![\(\begin{array}[t]{rll}
\lim\limits_{x\nearrow -3} f(x)&=+\infty& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0657ae8117a1c2e2b4f982866e028294c1b43f395c8487bed014adfccb18a1e9?color=5a5a5a)
![\(\begin{array}[t]{rll}
\lim\limits_{x\searrow -3} f(x)&=& -\infty \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6ef570d980cd12f5a40fe2f57f1c3ab234c702f6d68e7327a994d9358cdeb075?color=5a5a5a) Somit nimmt
Somit nimmt  alle möglichen Werte an und es gilt
alle möglichen Werte an und es gilt  .
3. Schritt: Asymptoten angeben
Eine senkrechte Asymptote hast du bereits mit der Definitionslücke bestimmt. Es gilt
.
3. Schritt: Asymptoten angeben
Eine senkrechte Asymptote hast du bereits mit der Definitionslücke bestimmt. Es gilt  .
Für die waagerechte Asympotet betrachtest du den Grenzwert
.
Für die waagerechte Asympotet betrachtest du den Grenzwert  :
:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to\pm\infty} f(x)&=& 1 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d4b0ba11a074063d96095abf2db2e857e3071a290f78ac6f93309ad2c0749d47?color=5a5a5a) Zusammen existieren die beiden Asympoten
Zusammen existieren die beiden Asympoten  und
und  .
.
 Gleichung angeben
Du sollst eine Gleichung für eine Funktion
Gleichung angeben
Du sollst eine Gleichung für eine Funktion  angeben, deren Graphen durch Verschiebung aus
angeben, deren Graphen durch Verschiebung aus  entsteht und welcher punktsymmetrisch zum Ursprung ist.
Durch eine Verschiebung um drei nach rechts ergibt sich ein Graph mit der Funktion
entsteht und welcher punktsymmetrisch zum Ursprung ist.
Durch eine Verschiebung um drei nach rechts ergibt sich ein Graph mit der Funktion  . Dieser ist punktsymmetrisch zu
. Dieser ist punktsymmetrisch zu  . Damit er dies zum Urspung ist wird er desweiteren um eins nach unten Verschoben es ergibt sich der Graph
. Damit er dies zum Urspung ist wird er desweiteren um eins nach unten Verschoben es ergibt sich der Graph  .
.
 Umkehrfunktion beschreiben
Du sollst beschreiben, wie man aus der Funktionsvorschrift von
Umkehrfunktion beschreiben
Du sollst beschreiben, wie man aus der Funktionsvorschrift von  die Umkehrfunktion bestimmen kann. Der Graph der Umkehrfunktion entsteht aus der Spiegelung an der ersten Winkelhalbierenden. Dies entspricht einem Vertauschen von
die Umkehrfunktion bestimmen kann. Der Graph der Umkehrfunktion entsteht aus der Spiegelung an der ersten Winkelhalbierenden. Dies entspricht einem Vertauschen von  und
und  .
Die Funktionsvorschrift wird also aus dem Vertauschen von
.
Die Funktionsvorschrift wird also aus dem Vertauschen von  und
und  und Auflösen nach
und Auflösen nach  bestimmt. Da die Umkehrfunktion aus der Vertauschen von
bestimmt. Da die Umkehrfunktion aus der Vertauschen von  und
und  entsteht, tauschen sich auch Werte- und Definitionsbereich, sodass
entsteht, tauschen sich auch Werte- und Definitionsbereich, sodass  und
und  gilt.
gilt.
 Winkel im Koordinatenursprung berechnen
Da die Inverse der Gespiegelten an der ersten Winkelhalbierenden entspricht, ist der Schnittwinkel das Doppelte des Winkels zwischen der Funktion und der Winkelhalbierenden, welche du mit dem Winkelsatz berechnen kannst:
Winkel im Koordinatenursprung berechnen
Da die Inverse der Gespiegelten an der ersten Winkelhalbierenden entspricht, ist der Schnittwinkel das Doppelte des Winkels zwischen der Funktion und der Winkelhalbierenden, welche du mit dem Winkelsatz berechnen kannst:
 Du benötigst die Ableitung von
Du benötigst die Ableitung von  , welche du mit folgendem Befehl berechnest:
, welche du mit folgendem Befehl berechnest:
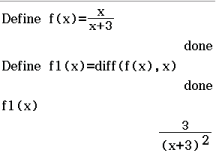 Abb. 4: Ableitung bestimmen
Mit dem Winkelsatz berechnest du den Winkel der Funktion zur
Abb. 4: Ableitung bestimmen
Mit dem Winkelsatz berechnest du den Winkel der Funktion zur  -Achse. Der Winkel der Winkelhalbierenden beträgt
-Achse. Der Winkel der Winkelhalbierenden beträgt  .
.
![\(\begin{array}[t]{rll}
\tan\varphi&=& f‘(0) &\quad \scriptsize \mid\; \arctan \\[5pt]
\varphi&=& \arctan (f‘(0)) \\[5pt]
&\approx & 18,43^\circ
\end{array}\)](https://mathjax.schullv.de/51339e9e081a8c72f8bf05a5ef67ed8850b1513705bd543aac8bdfc0332ffafc?color=5a5a5a) Der Winkel der Funktion zur
Der Winkel der Funktion zur  -Achse beträgt
-Achse beträgt  . Somit beträgt der Winkel
. Somit beträgt der Winkel  zwischen Funktion und Umkehrfunktion:
zwischen Funktion und Umkehrfunktion:
![\(\begin{array}[t]{rll}
\theta&=& 2\cdot (45^\circ-18,43^\circ) \\[5pt]
&=& 53,14^\circ
\end{array}\)](https://mathjax.schullv.de/3540e0f73103113f78f5cbe0a4da5f4aefab7cf4795cb82490d903d5ac1683a3?color=5a5a5a)
 schneidet
schneidet  in einem Winkel von
in einem Winkel von  .
.
 Seitenlänge bestimmen
Du sollst einen Seitenlänge des Rechtecks bestimmen, welches durch
Seitenlänge bestimmen
Du sollst einen Seitenlänge des Rechtecks bestimmen, welches durch  halbiert wird. Du suchst also eine Grenze für die Integrale, welchen den Flächeninhalt passend beschreiben. Verwende hierzu das Integral zwischen der Gerade
halbiert wird. Du suchst also eine Grenze für die Integrale, welchen den Flächeninhalt passend beschreiben. Verwende hierzu das Integral zwischen der Gerade  und
und  sowie das Integral für Flächen unterhalb einer Funktion.
Es ergibt sich die Gleichung:
sowie das Integral für Flächen unterhalb einer Funktion.
Es ergibt sich die Gleichung:
![\(\begin{array}[t]{rll}
\int\limits_0^a 1-f(x)\;\mathrm{d}x&=& \int\limits_0^a f(x)\;\mathrm{d}x \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f8ff2a7542ea3d0057f23e6530ea48d78ec8854879b7cd7dd996ce71c4295603?color=5a5a5a) Dieses Integral löst du mit dem solve Befehl:
Dieses Integral löst du mit dem solve Befehl:
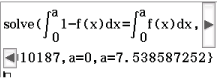 Abb. 5: Gleichung lösen mit dem Classpad
Du erhältst drei Lösungen, wobei allerdings nur
Abb. 5: Gleichung lösen mit dem Classpad
Du erhältst drei Lösungen, wobei allerdings nur  Sinn im Rahmen der Aufgabenstellung ergibt.
Sinn im Rahmen der Aufgabenstellung ergibt.
 Minimum begründen
Du sollst begründen, dass jede Funktion
Minimum begründen
Du sollst begründen, dass jede Funktion  für
für  ein Minimum besitzt, ohne dass du dabei die Ableitung verwendest. Betrachte dazu am besten die Nullstellenbedingung einer gebrochen rationalen Funktion.
Eine gebrochen rationale Funktion ist nur genau dann
ein Minimum besitzt, ohne dass du dabei die Ableitung verwendest. Betrachte dazu am besten die Nullstellenbedingung einer gebrochen rationalen Funktion.
Eine gebrochen rationale Funktion ist nur genau dann  wenn der Zähler
wenn der Zähler  ist. Im Falle von
ist. Im Falle von  also nur für
also nur für  . Da es sich bei
. Da es sich bei  um eine nach oben geöffnete Normalparabel handelt, liegt für
um eine nach oben geöffnete Normalparabel handelt, liegt für  ein Minimum vor. Diese Argumentation ist unabhängig von
ein Minimum vor. Diese Argumentation ist unabhängig von  und da
und da  ist, ist der Nenner immer positiv. Somit liegt für alle
ist, ist der Nenner immer positiv. Somit liegt für alle  bei
bei  ein Minimum vor.
ein Minimum vor.
 Wendepunkte auf Parallele zur
Wendepunkte auf Parallele zur  -Achse nachweisen
Du sollst nachweisen, dass alle Wendepunkte von
-Achse nachweisen
Du sollst nachweisen, dass alle Wendepunkte von  auf einer Parallelen zur
auf einer Parallelen zur  -Achsen liegen. Für Wendepunkte gilt, dass die zweite Ableitung einer Funktion
-Achsen liegen. Für Wendepunkte gilt, dass die zweite Ableitung einer Funktion  ist. Die Ableitung berechnest du erneut mit dem diff Befehl:
ist. Die Ableitung berechnest du erneut mit dem diff Befehl:
![\(\begin{array}[t]{rll}
f_k‘(x)&=& \frac{2\cdot k^2\cdot x}{(x^2+k^2)^2} \\[10pt]
f_k‘‘(x)&=& \frac{2\cdot k^4-6\cdot k^2\cdot x^2}{(x^2+k^2)^3} \\[10pt]
\end{array}\)](https://mathjax.schullv.de/44d7737ded20780291a0cdae3b40e5aa9fb7bac9b80a249a220783df362672b8?color=5a5a5a) Um auf die Nullstellen zu schließen, ist lediglich der Zähler zu betrachten.
Dies sind alle Wendepunkt des Graphen von
Um auf die Nullstellen zu schließen, ist lediglich der Zähler zu betrachten.
Dies sind alle Wendepunkt des Graphen von  . Um nachzuweisen, dass sie auf einer Parallelen zu
. Um nachzuweisen, dass sie auf einer Parallelen zu  -Achse liegen, berechnest du die
-Achse liegen, berechnest du die  -Koordinaten.
-Koordinaten.
![\(\begin{array}[t]{rll}
f_k\left(\pm\sqrt{\frac{1}{3}}\cdot k\right)&=& \frac{1}{4} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e7506a60fafb6cc9ea653ab81c4c7ba12bd0bdab4914e78233c24a2d59985c8d?color=5a5a5a) Beide Wendepunkt vom Graphen von
Beide Wendepunkt vom Graphen von  liegen auf der Parallelen zur
liegen auf der Parallelen zur  -Achse mit
-Achse mit  . Da dieser Wert nicht von
. Da dieser Wert nicht von  abhängt, liegen alle Wendepunkt der möglichen Funktionen der Schar auf dieser Parallelen.
abhängt, liegen alle Wendepunkt der möglichen Funktionen der Schar auf dieser Parallelen.
 Flächeninhalt berechnen und maximieren
Du sollst, für
Flächeninhalt berechnen und maximieren
Du sollst, für  , den Flächeninhalt des Dreiecks
, den Flächeninhalt des Dreiecks  zwischen den Punkten
zwischen den Punkten  ,
,  und
und  berechnen. Da es sich hierbei nicht um ein Recktwinkliges Dreieck handelt, da
berechnen. Da es sich hierbei nicht um ein Recktwinkliges Dreieck handelt, da  und
und  nicht die selbe
nicht die selbe  -Koordinate aufweisen, behilfst du dir über ein weiteres Dreieck
-Koordinate aufweisen, behilfst du dir über ein weiteres Dreieck  zwischen den Punkten
zwischen den Punkten  ,
,  und
und  .
Von diesem kannst du den Flächeninhalt normal berechnen.
.
Von diesem kannst du den Flächeninhalt normal berechnen.
![\(\begin{array}[t]{rll}
A_{p‘}&=& \frac{1}{2}\cdot p\cdot f_4(p)\\[5pt]
&=& \frac{1}{2}\cdot p\cdot\frac{p^2}{p^2+16} \\[5pt]
&=& \frac{p^3}{2\cdot (p^2+16)}
\end{array}\)](https://mathjax.schullv.de/84e4d2d29c364ef58cd45b770725161c9bd67ae59914c6df29b72e647f30ddb1?color=5a5a5a) Dabei ist
Dabei ist  um das Dreieck zwischen
um das Dreieck zwischen  ,
,  und
und  größer.
größer.
![\(\begin{array}[t]{rll}
A_p&=& A_{p‘}-\frac{1}{2}\cdot p\cdot 1 \\[5pt]
&=& \frac{p^3}{2\cdot (p^2+16)}-\frac{p}{2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/574842cf73f027b3e8951a6c39f3036fbd99bcd61e2b3658123b0c5a0ac2179f?color=5a5a5a) Diesen Ausdruck vereinfachst du mit dem Befehl simplify
Diesen Ausdruck vereinfachst du mit dem Befehl simplify
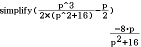 Abb. 6: Ausdruck vereinfachen
Flächeninhalte an sich sind positiv, deshalb betrachtest du den Betrag.
Abb. 6: Ausdruck vereinfachen
Flächeninhalte an sich sind positiv, deshalb betrachtest du den Betrag.
![\(\begin{array}[t]{rll}
A_p&=& \frac{8\cdot p}{p^2+16} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3ad580839a903ee9ef47af477e961f2e2392288d5430388b5b49704e7511ab31?color=5a5a5a) Abschließend sollst du den maximalen Flächeninhalt oder eben das Maximum von
Abschließend sollst du den maximalen Flächeninhalt oder eben das Maximum von  bestimmen. Diesn bestimmst du mit dem Befehl fMax:
bestimmen. Diesn bestimmst du mit dem Befehl fMax:
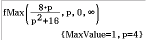 Abb. 7: Maximum bestimmen
Das Maximum der Dreiecksfläceh beträgt
Abb. 7: Maximum bestimmen
Das Maximum der Dreiecksfläceh beträgt  an der Stelle
an der Stelle  .
.
 Graph zeichnen
Du sollst den Graphen der Funktion
Graph zeichnen
Du sollst den Graphen der Funktion  im Intervall
im Intervall ![\(\left[-25 \, ; \, 175\right]\)](https://mathjax.schullv.de/55348b4038f774c4652f8ec09c0f618aafffdbc75568c39b442464d7810064bd?color=5a5a5a) zeichnen.
Bei der Funktion handelt es sich um einen gestreckte Sinus. Bestimme mit dem TR die kritischen Punkte im betrachteten Intervall.
zeichnen.
Bei der Funktion handelt es sich um einen gestreckte Sinus. Bestimme mit dem TR die kritischen Punkte im betrachteten Intervall.
 Abb. 8: Graph zeichnen
Abb. 8: Graph zeichnen
 Schrittweise Umwandlung einer
Schrittweise Umwandlung einer  -Funktion
Du sollst angeben wie der Graph von
-Funktion
Du sollst angeben wie der Graph von  aus dem Graphen einer normalen Sinus-Funktion hervorgeht.
Dies geschieht in zwei Schritten. Zuerst wird die Periode mit dem Faktor
aus dem Graphen einer normalen Sinus-Funktion hervorgeht.
Dies geschieht in zwei Schritten. Zuerst wird die Periode mit dem Faktor  angepasst. Dies entspricht einer Streckung entlang der
angepasst. Dies entspricht einer Streckung entlang der  -Achse.
Danach wird der Graph entlang der
-Achse.
Danach wird der Graph entlang der  -Achse gestreckt. Die Amplitude wird auf
-Achse gestreckt. Die Amplitude wird auf  erhöht.
erhöht.
 Mittlere Dicke bestimmen
Du sollst unter Verwendung der Kurvenlänge und der Konitnuität des Volumens die mittlere Dicke des Blechs nach der Umformung zu Wellblech bestimmen. Betrachte hierzu die Ausgangssituation.
1. Schritt: Volumen bestimmen
Zu Beginn ist das Blech quadratisch, einen Meter lang und zwei Milimeter bzw.
Mittlere Dicke bestimmen
Du sollst unter Verwendung der Kurvenlänge und der Konitnuität des Volumens die mittlere Dicke des Blechs nach der Umformung zu Wellblech bestimmen. Betrachte hierzu die Ausgangssituation.
1. Schritt: Volumen bestimmen
Zu Beginn ist das Blech quadratisch, einen Meter lang und zwei Milimeter bzw.  m dick. Für das Volumen
m dick. Für das Volumen  gilt:
gilt:
![\(\begin{array}[t]{rll}
V&=& 1\cdot 1\cdot 0,002 \\[5pt]
&=& 0,002
\end{array}\)](https://mathjax.schullv.de/d149af8caccc6a010652115f61b482571ed8a037cbee96a6749b42232e89da19?color=5a5a5a) Vor der Umformung beträgt des Volumen
Vor der Umformung beträgt des Volumen  m
m .
2. Schritt: Kurvenlänge bestimmen
Mit der angegebenen Formel bestimmst du die Kurvenlänge
.
2. Schritt: Kurvenlänge bestimmen
Mit der angegebenen Formel bestimmst du die Kurvenlänge  zwischen den beiden Grenzen
zwischen den beiden Grenzen  und
und  , da
, da  mm einem Meter entsprechen.
Die Ableitung von
mm einem Meter entsprechen.
Die Ableitung von  bestimmst du erneut mit dem diff Befehl.
bestimmst du erneut mit dem diff Befehl.
![\(\begin{array}[t]{rll}
l&=& \int\limits_0^{1.000} \sqrt{1+\left[ w‘(x) \right]^2}\;\mathrm{d}x \\[5pt]
&\approx& 1.219,56
\end{array}\)](https://mathjax.schullv.de/b9bda0acc33c5833cd6b13c7a1b37cd5326012593f0b635a8ce9a6a8e8a14e5f?color=5a5a5a) Die Länge des Wellblechs beträgt
Die Länge des Wellblechs beträgt  mm oder
mm oder  m.
3. Schritt: Dicke bestimmen
Mit dieser Angabe kannst du aus dem Volumen des ersten Schrittes die Dicke des Wellblechs bestimmen.
Die Dicke beträgt
m.
3. Schritt: Dicke bestimmen
Mit dieser Angabe kannst du aus dem Volumen des ersten Schrittes die Dicke des Wellblechs bestimmen.
Die Dicke beträgt  mm.
mm.
 Volumen des Hohlraums bestimmen
Du sollst das Volumen bestimmen, welches mit Bauschaum aufgefüllt werden muss. Nimmst du die ebene Dachfläche als
Volumen des Hohlraums bestimmen
Du sollst das Volumen bestimmen, welches mit Bauschaum aufgefüllt werden muss. Nimmst du die ebene Dachfläche als  -Achse an, verändert sich die Funktion
-Achse an, verändert sich die Funktion  , da der Graph nach oben verschoben werden muss, damit seine Tiefpunkte auf der Achse liegen. Nenne die neue Funktion
, da der Graph nach oben verschoben werden muss, damit seine Tiefpunkte auf der Achse liegen. Nenne die neue Funktion  .
.
![\(\begin{array}[t]{rll}
W(x)&=& w(x)+13,5 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a9be9ffa3ec33369c2bf42f0eaa4c16f3a10a72b3a4659dc9343632b55aff7a5?color=5a5a5a) Für das Volumen des Bauschaums bestimmst du zuerst die Größe der Querschnittsfläche respektive das Integral über
Für das Volumen des Bauschaums bestimmst du zuerst die Größe der Querschnittsfläche respektive das Integral über  .
.
![\(\begin{array}[t]{rll}
A&=& \int\limits_{0}^{1000} W(x)\;\mathrm{d}x \\[5pt]
&\approx& 20.189,5
\end{array}\)](https://mathjax.schullv.de/53e69daf4d17a471acb8434eb5828872e9a3c26bc9fa01e3e3462c6963bee067?color=5a5a5a) Mit dieser Querschnittsfläche kannst du das benötigte Volumen des Bauschaums berechnen.
Mit dieser Querschnittsfläche kannst du das benötigte Volumen des Bauschaums berechnen.
![\(\begin{array}[t]{rll}
V&=& 0,0201895\cdot 1 \\[5pt]
&\approx& 0,02
\end{array}\)](https://mathjax.schullv.de/fee11122bd8c78e4be294f977a6efaa4fd9fb3bdb5029cd1bedc544541193882?color=5a5a5a) Es werden
Es werden  m
m Schaum benötigt.
Schaum benötigt.
1)
a)
b)
Keyboard  Math1
Math1
 Abb. 1: Gleichungssystem lösen mit dem Classpad
Abb. 1: Gleichungssystem lösen mit dem Classpad
2)
a)
b)
Interactive  Advanced
Advanced  solve
solve
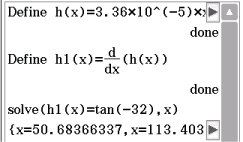 Abb. 2: Gleichung lösen mit dem Classpad
Abb. 2: Gleichung lösen mit dem Classpad
3)
a)
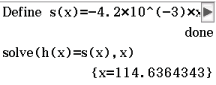 Abb. 3: Gleichung lösen mit dem Classpad
Abb. 3: Gleichung lösen mit dem Classpad
b)
c)
d)
e)
f)
g)
: Springer springt am Absprungpunkt ab
: Daraus lässt sich der Winkel im Absprung berechnen
: Der Springer landet bei
Erster Springer
![\(\begin{array}[t]{rll}
\varphi&=& \arctan (s‘(0)) \\[5pt]
&\approx& -5,71^\circ
\end{array}\)](https://mathjax.schullv.de/84ffbb21bea2737921a568675c104d7fcf2456a42982e15b0ee7a47287278e34?color=5a5a5a)
Zweiter Springer
![\(\begin{array}[t]{rll}
\theta&=& \arctan (t‘(0) ) \\[5pt]
&\approx& -4,97^\circ
\end{array}\)](https://mathjax.schullv.de/cd41e44529b37456119ee5a9c338a80ec6c02c085070506e4b6e9a7d3fcead20?color=5a5a5a)
Ebenfalls der erste Springer springt unter dem größeren Winkel ab.
1)
a)
b)
c)
d)
Interactive  Calculation
Calculation  diff
diff
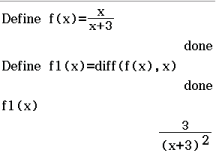 Abb. 4: Ableitung bestimmen
Abb. 4: Ableitung bestimmen
e)
Interactive  Advanced
Advanced  solve
solve
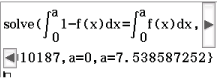 Abb. 5: Gleichung lösen mit dem Classpad
Abb. 5: Gleichung lösen mit dem Classpad
2)
a)
b)
c)
Interactive  Transformation
Transformation  simplify
simplify
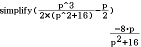 Abb. 6: Ausdruck vereinfachen
Abb. 6: Ausdruck vereinfachen
Interactive  Calculation
Calculation  fMin/fMax
fMin/fMax  fMax
fMax
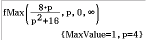 Abb. 7: Maximum bestimmen
Abb. 7: Maximum bestimmen
3)
a)
 Abb. 8: Graph zeichnen
Abb. 8: Graph zeichnen
b)
c)
d)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.