Teil B

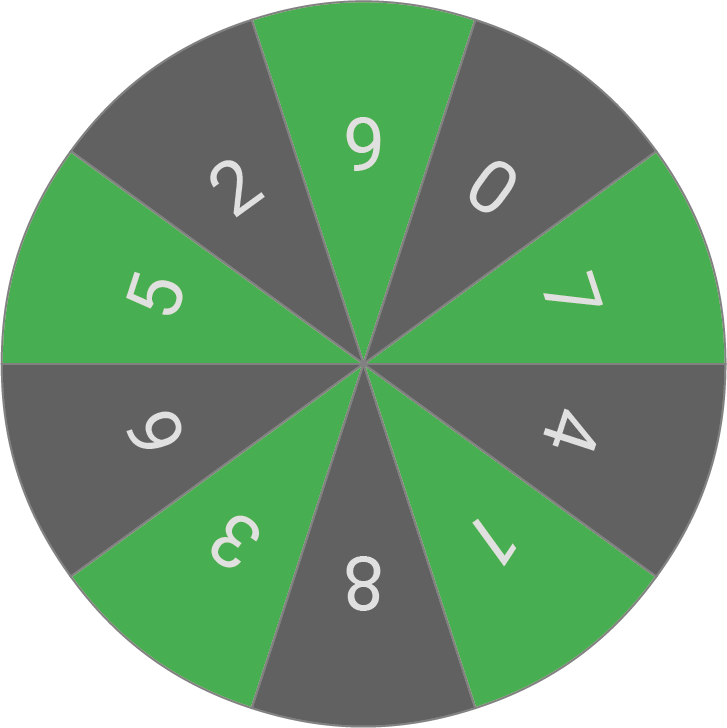
Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von 0 bis 9 durchnummeriert.

Das Glücksrad wird zwanzigmal gedreht. Bestimme die Wahrscheinlichkeiten der Ereignisse $A$ und $B$ .

$A:$

„Es wird genau siebenmal eine ungerade Zahl erzielt.“

$B:$

„Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt.“

(3 BE)

Das Glücksrad wird zweimal gedreht. Untersuche, ob die Ereignisse C und $D$ stochastisch unabhängig sind.

$C:$

„Die Summe der erzielten Zahlen ist kleiner als 4.“

$D:$

„Das Produkt der erzielten Zahlen ist 2 oder 3.“

(5 BE)

Mit dem Glücksrad wird ein Spiel durchgeführt. Jeder Spieler darf das Glücksrad beliebig oft drehen. Beendet er das Spiel selbst, bevor er eine „0“ erzielt, so wird ihm die Summe der erzielten Zahlen in Euro ausgezahlt. Erzielt er eine „0“, so ist das Spiel dadurch beendet und es erfolgt keine Auszahlung.

Ein erster Spieler entscheidet sich vor dem Spiel dafür, das Glücksrad, sofern er keine „0“ erzielt, viermal zu drehen und danach das Spiel zu beenden. Bestimme die Wahrscheinlichkeit dafür, dass er eine Auszahlung erhält.

(2 BE)

Bei einem zweiten Spieler beträgt nach mehrmaligem Drehen des Glücksrads die Summe der erzielten Zahlen 60. Er möchte nun das Spiel entweder sofort beenden oder das Glücksrad genau ein weiteres Mal drehen. Berechne für den Fall, dass sich der Spieler für die weitere Drehung entscheiden sollte, den Erwartungswert für die Auszahlung. Gib eine Empfehlung ab, ob sich der Spieler für das Beenden des Spiels oder für die weitere Drehung entscheiden sollte, und begründe deine Empfehlung.

(4 BE)

Wenn sich ein Spieler vor dem Spiel dafür entscheidet, das Glücksrad, sofern er keine „0“ erzielt, $n$ -mal zu drehen, dann kann der Erwartungswert für die Auszahlung mit dem Term $5n \cdot 0,9^n$ berechnet werden. Beurteile die folgende Aussage:
$\quad$ Es gibt zwei, aber nicht drei aufeinanderfolgende Werte von $n$ , für die die Erwartungswerte für die Auszahlung übereinstimmen.

(4 BE)

Im Folgenden wird ein Glücksrad mit $n$ gleich großen Sektoren, die mit den Zahlen von $0$ bis $n-1$ durchnummeriert sind, betrachtet.

Bestimme für $n=5$ die Wahrscheinlichkeit dafür, dass bei dreimaligem Drehen des Glücksrads genau zwei gleiche Zahlen erzielt werden.

(3 BE)

Das Glücksrad wird $n$ -mal gedreht. Ermittle den kleinstmöglichen Wert von $n,$ für den die Wahrscheinlichkeit dafür, dass alle Zahlen verschieden sind, kleiner als $1\,\%$ ist.

(4 BE)

(25 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Betrachtet wird die Zufallsgröße $X,$ die die zufällige Anzahl der erzielten ungeraden Zahlen bei zwanzig Drehungen des Glücksrades beschreibt. $X$ kann als binomialverteilt mit $n=20$ und $p=\frac{5}{10} =0,5$ betrachtet werden.

$P(A)=P_{0,5}^{20}(X=7)$ $= B(0,5;20;7)$ $\approx 0,0739$ $= 7,39\,\%$

$\begin{array}[t]{rll} P(B)&=& P_{0,5}^{20}(7\lt X\leq12) \\[5pt] &=& P_{0,5}^{20}(X\leq12)-P_{0,5}^{20}(X\leq7) \\[5pt] &=& F_{0,5}^{20}(12)-F_{0,5}^{20}(7) \\[5pt] &\approx& 0,8684 - 0,1316 \\[5pt] &=& 73,68\,\% \end{array}$

Die beiden Ereignisse $C$ und $D$ sind stochastisch unabhängig, wenn $P(C\cap D) = P(C)\cdot P(D)$ gilt.

Zu Ereignis $C$ gehören insgesamt die folgenden zehn Ergebnisse:

$(0;0),$ $(0;1),$ $(0;2),$ $(0;3)$
$(1;0),$ $(1;1),$ $(1;2)$
$(2;0),$ $(2;1)$
$(3;0)$

Zu Ereignis $D$ gehören insgesamt die folgenden vier Ergebnisse:

$(1;2),$ $(1;3)$
$(2;1)$
$(3;1)$

Die Wahrscheinlichkeit eines Ergebnisse ergibt sich zu:

$\frac{1}{10}\cdot \frac{1}{10} =\frac{1}{100}$

Mit der Pfadadditionsregel folgt:

$P(C) = 10\cdot \frac{1}{100} =0,1$

$P(D) = 4\cdot \frac{1}{100} = 0,04$

Die Schnittmenge der beiden Ereignisse $C$ und $D$ sind $(1;2)$ und $(2;1),$ somit gilt:

$P(C\cap D)$ $= 2\cdot \frac{1}{100}$ $= 0,02.$

Es folgt:

$P(C)\cdot P(D)$ $= 0,04\cdot 0,1$ $= 0,004 \neq P(C\cap D)$

Somit sind die Ereignisse $C$ und $D$ nicht stochastisch unabhängig.

Der Spieler erhält eine Auszahlung, wenn in allen vier Drehungen keine Null erzielt wird.
Die Wahrscheinlichkeit, keine Null zu erzielen beträgt $\frac{9}{10}=0,9.$ Die Wahrscheinlichkeit dafür, dass der Spieler eine Auszahlung erhält, beträgt somit:

$0,9\cdot0,9\cdot0,9\cdot0,9$ $= 0,6561$ $= 65,61\,\%$

Mit einer Wahrscheinlichkeit von $65,61\,\%$ erhält der Spieler eine Auszahlung.

Erwartungswert für die Auszahlung berechnen

$X:$ Wert der Auszahlung in Euro

Jede Zahl hat die gleiche Wahrscheinlichkeit, erzielt zu werden. Somit folgt:

$E(X)$ $= \frac{1}{10}\cdot 0+\frac{1}{10}\cdot61$ $+\frac{1}{10}\cdot 62+\frac{1}{10}\cdot 63$ $+\frac{1}{10}\cdot64+\frac{1}{10}\cdot65$ $+\frac{1}{10}\cdot66+\frac{1}{10}\cdot67$ $+\frac{1}{10}\cdot68+\frac{1}{10}\cdot69$ $= 58,5\,[€]$

Empfehlung abgeben

Da der Erwartungswert für die Auszahlung nach einer weiteren Drehung mit $E(X)=58,5\,[€]$ kleiner ist als die Auszahlung von $60\,€$ ohne diese Drehung des Glückrads, sollte sich der Spieler für das Beenden des Spiels entscheiden.

Damit für zwei aufeinanderfolgende Werte von $n$ der Erwartungswert übereinstimmt, muss ein $n$ mit $5n\cdot0,9^n$ $= 5(n+1)\cdot0,9^{n+1}$ existieren. Es folgt:

$\begin{array}[t]{rll} 5n\cdot0,9^n&=&5(n+1)\cdot0,9^{n+1} &\quad \scriptsize \mid\;:0,9^{n}\neq 0 \\[5pt] 5n &=& 5(n+1)\cdot 0,9 &\quad \scriptsize \mid\;:5 \\[5pt] n &=& (n+1)\cdot 0,9 \\[5pt] n &=& 0,9n+ 0,9 &\quad \scriptsize \mid\;-0,9n \\[5pt] 0,1n &=& 0,9 &\quad \scriptsize \mid\;\cdot 10 \\[5pt] n&=& 9 \\[5pt] \end{array}$

Der Erwartungswert für die Auszahlung ist somit für $9$ und $10$ Drehungen gleichgroß. Da die Gleichung nur eine Lösung besitzt, kann es zudem keine drei aufeinanderfolgenden Werte für $n$ geben, für die das gilt. Somit ist die Aussage aus der Aufgabenstellung korrekt.

Die Wahrscheinlichkeit, eine bestimmte Zahl zu erzielen, beträgt für alle $5$ Zahlen $\frac{1}{5}.$ Die Wahrscheinlichkeit, eine bestimmte Zahl bei dreimaligem Drehen genau zweimal zu erzielen ergibt sich zu:

$\pmatrix{3\\1}\cdot\dfrac{1}{5}\cdot\dfrac{1}{5}\cdot\dfrac{4}{5}$

Da das für jede beliebige der $5$ Zahlen gilt, folgt für die Wahrscheinlichkeit, dass bei dreimaligem Drehen des Glücksrads genau zwei gleiche Zahlen erzielt werden:

$5\cdot\pmatrix{3\\1}$ $\cdot\dfrac{1}{5}\cdot\dfrac{1}{5} \cdot\dfrac{4}{5}$ $= 15\cdot\dfrac{4}{125} = 0,48 = 48\,\%$

Die Wahrscheinlichkeit, dass alle Zahlen verschieden sind, beträgt bei $n$ Drehungen:

$p_n =\dfrac{n}{n}\cdot\dfrac{n-1}{n} \cdot\dfrac{n-2}{n}\cdot\ldots\cdot\dfrac{1}{n}$ $= \dfrac{n!}{n^n}.$

Durch systematisches Ausprobieren folgt:

$p_6$ $= \dfrac{6\cdot5\cdot4\cdot3\cdot2\cdot1}{6^6}$ $= \dfrac{720}{46656} \approx 0,0154$ $= 1,54\,\%$

$p_7$ $= \dfrac{7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}{7^7}$ $= \dfrac{5040}{823543} \approx 0,0061$ $= 0,61\,\%$

Somit ist $n=7$ der kleinstmögliche Wert.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?