Teil A
Ein Glücksrad ist in 20 gleich große Sektoren unterteilt, die entweder blau oder gelb eingefärbt sind. Das Glücksrad wird 100-mal gedreht. Die binomialverteilte Zufallsgröße 
beschreibt, wie oft dabei die Farbe „Blau“, die binomialverteilte Zufallsgröße 
wie oft dabei die Farbe „Gelb“ erzielt wird.
a)
Begründe, dass und 
die gleiche Standardabweichung haben.
(2 BE)
b)
Der Erwartungswert von ist ganzzahlig. Die Abbildung zeigt Werte der Wahrscheinlichkeitsverteilung von 
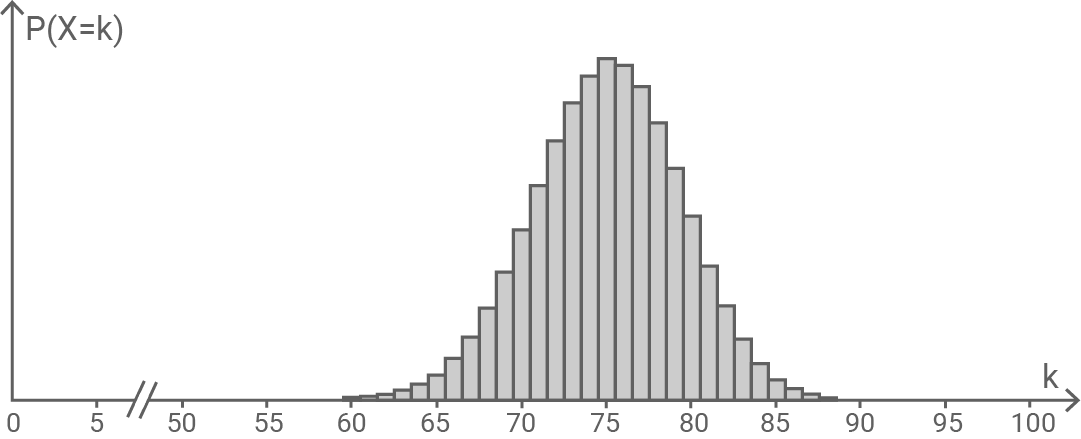Bestimme die Anzahl der blauen Sektoren des Glücksrads.
(3 BE)
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Für die Standardabweichung gilt:
Der Parameter 
ist bei beiden Verteilung gleich und entspricht den 100 Drehungen.
Da außerdem jeweils die Wahrscheinlichkeit 
und die Gegenwahrscheinlichkeit 
multipliziert werden, wird bei beiden Standardabweichungen die Wahrscheinlichkeit für „Blau“ und für „Gelb“ multipliziert.
Damit haben und folglich die gleiche Standardabweichung.
b)
Aus der Wahrscheinlichkeitsverteilung von kann der Erwartungswert 
abgelesen werden.
Es gilt:
![\(\begin{array}[t]{rll}
\mu&=& n\cdot p& \\[5pt]
75&=& 100\cdot \dfrac{x}{20}&\quad \scriptsize \mid\; :100 \\[5pt]
0,75&=& \dfrac{x}{20}&\quad \scriptsize \mid\; \cdot 20 \\[5pt]
15&=& x
\end{array}\)](https://mathjax.schullv.de/f173228a1a0df5565b9c5226b3de2b15f02a5c901b8273c1b947d0a9a950934a?color=5a5a5a)
Das Glücksrad besitzt somit 15 blaue Sektoren.