Teil B

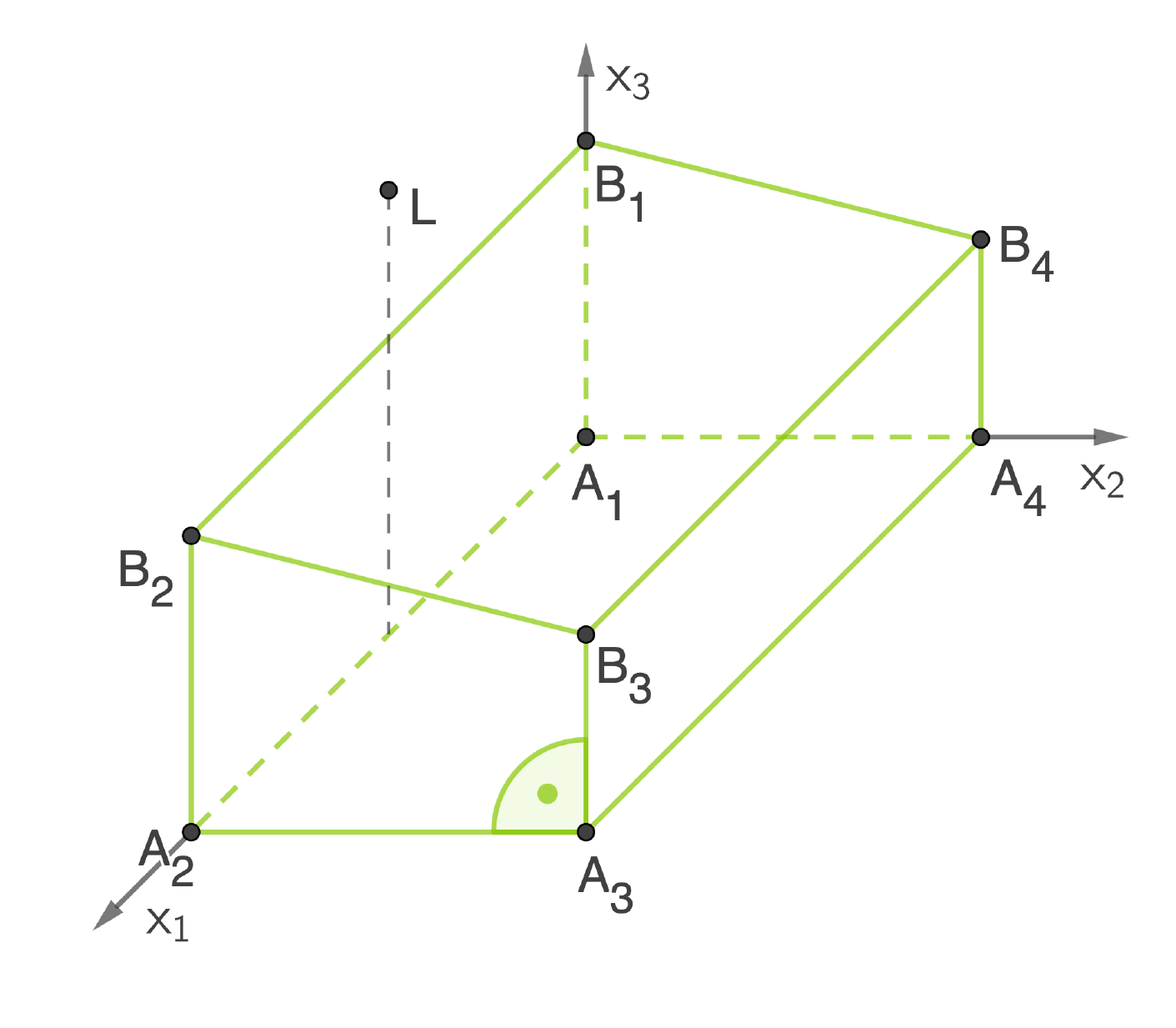
Die Abbildung 1 zeigt modellhaft eine Mehrzweckhalle, die auf einer horizontalen Fläche steht und die Form eines geraden Prismas hat.

Die Punkte $A_1(0 \mid 0 \mid 0)$ , $A_2(20 \mid 0 \mid 0)$ , $A_3$ und $A_4(0 \mid 10 \mid 0)$ stellen im Modell die Eckpunkte der Grundfläche der Mehrzweckhalle dar, die Punkte $B_1$ , $B_2$ , $B_3$ und $B_4$ die Eckpunkte der Dachfläche. Diejenige Seitenwand, die im Modell in der $x_1 x_3$ -Ebene liegt, ist $6\, \text{m}$ hoch, die ihr gegenüberliegende Wand nur $4\,\text{m}$ .

Eine Längeneinheit im Koordinatensystem entspricht $1\, \text{m}$ , d.h. die Mehrzweckhalle ist $20\, \text{m}$ lang.

Grafik eines Quaders mit Eckpunkten und Achsenbeschriftungen in einem dreidimensionalen Koordinatensystem.

Abb. 1

Gib die Koordinaten der Punkte $B_2$ , $B_3$ und $B_4$ an und bestätige, dass diese Punkte in der Ebene $E: x_2+ 5x_3 -30 =0$ liegen. Gib die besondere Lage von $E$ im Koordinatensystem an.

(5 BE)

Berechne die Größe des Neigungswinkels $\varphi$ der Dachfläche gegenüber der Horizontalen. Beurteile, ob der Ansatz $\overline{A_1 A_2} \cdot \overline{A_2 A_3} \cdot cos (\varphi)$ zur Berechnung des Inhalts der Dachfläche in Quadratmetern geeignet ist.

(4 BE)

Der Punkt $T\,(7 \mid 10 \mid 0)$ liegt auf der Kante $[A_3 A_4]$ .
Untersuche rechnerisch, ob es Punkte auf der Kante $[B_3 B_4]$ gibt, für die gilt:
Die Verbindungsstrecken des Punktes zu den Punkten $B_1$ und $T$ stehen aufeinander senkrecht. Gib gegebenenfalls die Koordinaten dieser Punkte an.

(5 BE)

Der Punkt $L$ , der vertikal über dem Mittelpunkt der Kante $[A_1 A_2]$ liegt, veranschaulicht im Modell die Position einer Flutlichtanlage, die $12\, \text{m}$ über der Grundfläche angebracht ist.
Die als punktförmig angenommene Lichtquelle beleuchtet - mit Ausnahme des Schattenbereichs in der Nähe der Hallenwände - das gesamte Gelände um die Halle.

Die Punkte $L$ , $B_2$ und $B_3$ legen eine Ebene $F$ fest. Ermittle eine Gleichung von $F$ in Normalenform.

$\big[$ zur Kontrolle: $F : 3x_1 +x_2 +5x_3 -90=0 \big]$

(4 BE)

Die Ebene $F$ schneidet die $x_1 x_2$ - Ebene in der Gerade $g$ . Bestimme eine Gleichung von $g$ .

$\big[$ zur Kontrolle: $g: \overrightarrow{X} = \pmatrix{30\\0\\0}+\lambda \cdot \pmatrix{1\\-3\\0},$ $\lambda\in\mathbb{R}\big]$

(3 BE)

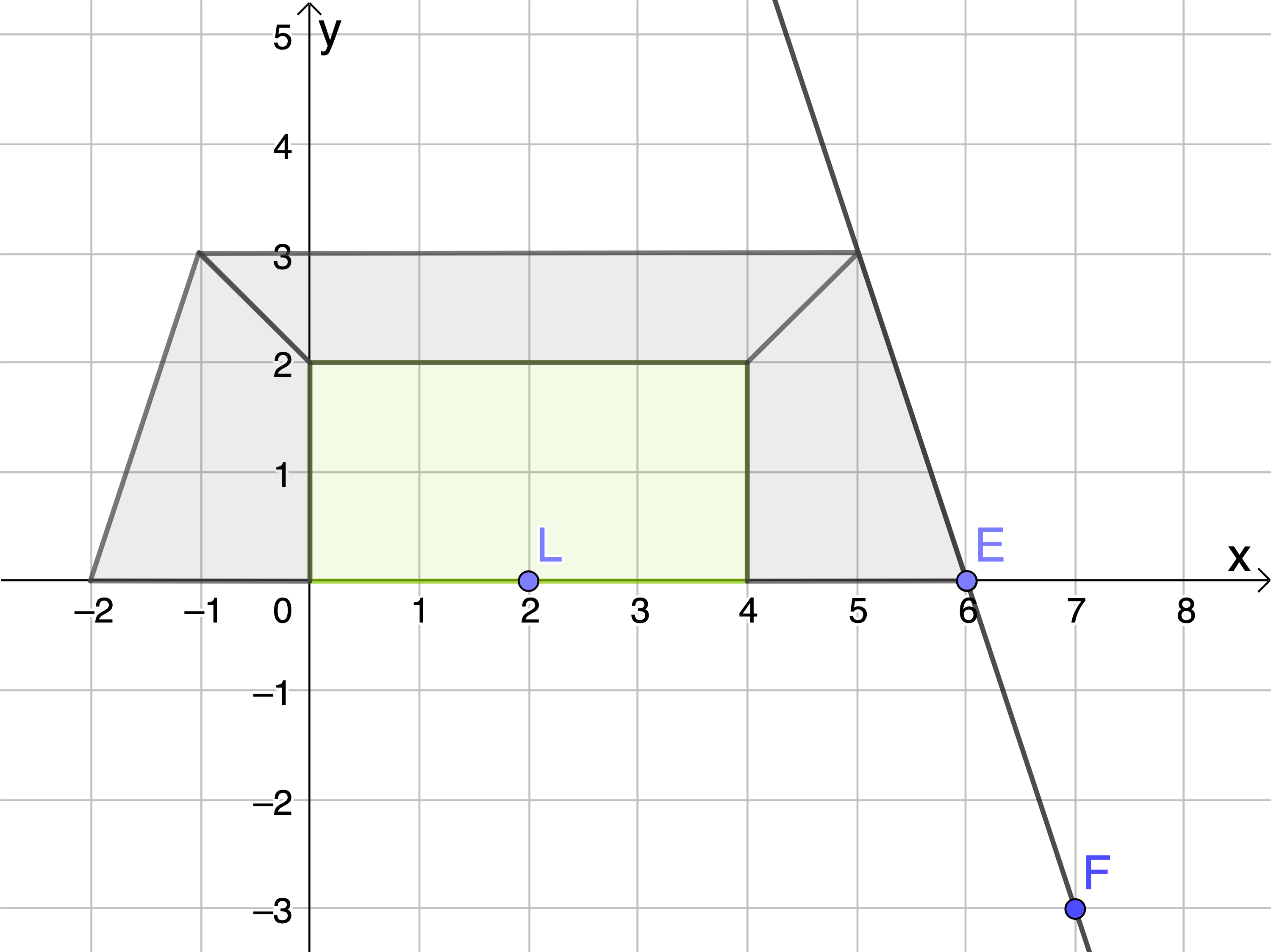
Die Abbildung 2 zeigt den Grundriss des Hallenmodells in der $x_1 x_2$ - Ebene.
Stelle unter Verwendung der bisherigen Ergebnisse den Schattenbereich der Flutlichtanlage in der Abbildung exakt dar.

Graf mit einem grünen Rechteck im Koordinatensystem, x1 und x2 Achsen sichtbar.

Abb. 2

(4 BE)

(25 BE)

Die Punkte kannst du einfach ablesen: $B_2 (20 \mid 0 \mid 6), \, B_3(20\mid 10 \mid 4), \, B_4(0 \mid 10 \mid 4)$ .
Setze die Koordinaten in die Ebenengleichung ein, um zu schauen ob die Punkte auf der Ebene liegen.

Punkt $B_2 (20 \mid 0 \mid 6)$ :
$\begin{array}[t]{rll} 0 + 5 \cdot 6 -30&=&0 &\quad \scriptsize \\[5pt] 0&=&0 \end{array}$

Punkt $B_3(20\mid 10 \mid 4)$ :
$\begin{array}[t]{rll} 10 + 5 \cdot 4 -30&=&0 &\quad \scriptsize \\[5pt] 0&=&0 \end{array}$

Punkt $B_4(0 \mid 10 \mid 4)$ :
$\begin{array}[t]{rll} 10 + 5 \cdot 4 -30&=&0 &\quad \scriptsize \\[5pt] 0&=&0 \end{array}$

Die Punkte liegen folglich alle in der Ebene.

Besonders an der Ebene $E:x_2 +5x_3 -30=0$ ist, dass sie parallel zur $x_1$ -Achse verläuft.

Winkel
Einen Normalenvektor der Ebene $E$ kannst du aus der Ebenengleichung ablesen. Er entspricht $\overrightarrow{n}= \pmatrix{0\\1\\5}$ . Ein Normalenvektor der $x_1x_2$ - Ebene lautet $\overrightarrow{n_{x_1x_2}}= \pmatrix{0\\0\\1}$ .
Den Winkel zwischen den beiden Ebenen berechnest du mit:

$\cos(\varphi)= \dfrac{\pmatrix{0\\1\\5} \circ \pmatrix{0\\0\\1}}{\left| \pmatrix{0\\1\\5}\right| \cdot \left| \pmatrix{0\\0\\1} \right| }$ $= \dfrac{5}{\sqrt{1^2+5^2} \cdot \sqrt{1^2}}$

$\varphi \approx \cos^{-1} (0,98) \approx 11,5 ^{\circ}$ .

Dachfläche
Die Dachfläche wird durch das Rechteck $B_1B_2B_3B_4$ beschrieben.
Die Länge der Strecke Strecke $\overline{B_3B_4}$ entspricht der Länge der Strecke $\overline{A_3A_4}$ .

Mit $\overline{A_2A_3}$ und dem Winkel $\varphi$ kann folgende Gleichung zur Berechnung der Strecke $\overline{B_2B_3}$ aufgestellt werden: $\overline{B_2B_3} = \overline{A_2A_3} \cdot \dfrac{1}{cos(\varphi)}$ .

Der Ansatz ist falsch, richtig würde er lauten: $A_D=\overline{A_1A_2} \cdot \overline{A_2A_3} \cdot \dfrac{1}{cos(\varphi)} .$

Ein beliebiger Punkt auf der Strecke $[B_3 B_4]$ liegt auf der Geraden $g : \overrightarrow{x} = \pmatrix {20\\10\\4} +s \cdot \pmatrix{-20\\0\\0}$ und somit hat ein beliebiger Punkt C auf $g$ die Koordinaten $C(20-20s \mid 10 \mid 4)$ .

Gesucht ist das s, für welches die Strecken $[CT]$ und $[CB_1]$ senkrecht stehen.

$\overrightarrow{CT} = \pmatrix{7\\10\\0} -\pmatrix{20-20s \\10\\4} = \pmatrix{-13+20s\\0\\-4}$

$\overrightarrow{CB_1} =\pmatrix{0\\0\\6}-\pmatrix{20-20s \\10\\4} = \pmatrix{-20+20s\\-10\\2}$

$\pmatrix{-13+20s\\0\\-4} \circ \pmatrix{-20+20s\\-10\\2} = 0$

$\begin{array}[t]{rll} (-13+20s) \cdot (-20+20s) +(-8)&=& 0&\quad \scriptsize \\[5pt] 400s^2 -660s+252&=&0 \end{array}$

Mit der pq-Formel kommst du auf $s_1=1,05$ und $s_2=0,6$ .

Setzt du s in C ein, kommst du auf die Koordinaten $C_1(-1 \mid 10 \mid 4)$ und $C_2(8\mid 10 \mid 4)$ . Nur $C_2$ liegt zwischen $B_3$ und $B_4$ , deshalb ist $C_2$ der gesuchte Punkt.

Die Koordinaten des Punktes L sind $L(10 \mid 0 \mid 12)$ .

Um die Ebenengleichung in Normalenform aufzustellen, musst du zunächst einen Normalenvektor berechnen:

$\overrightarrow{LB_2} = \pmatrix{20\\0\\6} - \pmatrix{10\\0\\12} = \pmatrix{10\\0\\-6}$

$\overrightarrow{LB_3} =\pmatrix{20\\10\\4} - \pmatrix{10\\0\\12} = \pmatrix{10\\10\\-8}$

Ein Normalenvektor ist das Kreuzprodukt der Richtungsvektoren.

$\overrightarrow{n}=\pmatrix{10\\0\\-6} \times \pmatrix{10\\10\\-8} = \pmatrix{60\\20\\100} = 20 \cdot \pmatrix{3\\1\\5}$

Die Normalenform lautet folglich $F : \pmatrix{3\\4\\5} \circ \left[\overrightarrow{ x} -\pmatrix{10\\0\\12} \right] =0$ .

Durch Ausmultiplizieren kommst du auf die Koordinatenform von $F$ .

Für die $x_1x_2$ -Ebene gilt $x_3=0$ .

$\begin{array}[t]{rll} 3x_1 +x_2 +3x_3 -90&=&0 &\quad \scriptsize \mid\; +90 \mid \; x_3=0\\[5pt] 3x_1+x_2 &=&90 &\quad \scriptsize \mid\;-x_2 \\[5pt] 3x_1&=&90-x_2 &\quad \scriptsize \mid\; :3\\[5pt] x_1&=&30- \dfrac{1}{3}x_2 &\quad \scriptsize \\[5pt] \end{array}$

Setze $x_2=t.$ Somit kannst du $x_1=30-\dfrac{1}{3}t$ , $x_2=t$ und $x_3=0$ als Vektor schreiben und somit die Gerade aufstellen.

$\pmatrix{30-\dfrac{1}{3}t \\ t\\ 0}= \pmatrix{30\\0\\0} +t \cdot \pmatrix{-\frac{1}{3} \\1\\0}$ .

Der Richtungsvektor kann noch vereinfacht werden. Somit schneidet die Ebene $F$ die $x_1x_2$ -Ebene in der Geraden $g : \overrightarrow{x} = \pmatrix{30\\0\\0}+t \cdot \pmatrix{1\\-3\\0}.$

Grafische Darstellung einer Funktion mit einem Rechteck im Koordinatensystem. Punkte L, E und F sind markiert.

Die Gerade stellt die Schnittgerade aus Aufgabe e) dar.