Geometrie Prüfungsteil A

Aufgabengruppe 1

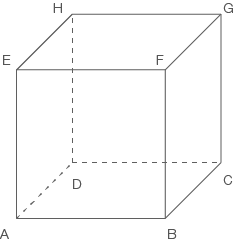
Betrachtet wird der abgebildete Würfel $ABCDEFGH$ .
Die Eckpunkte $D$ , $E$ , $F$ und $H$ dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: $D(0\mid 0\mid -2)$ , $E(2\mid 0 \mid 0)$ , $F(2\mid 2\mid 0)$ und $H(0\mid 0\mid 0)$ .

Draufsicht auf einen Würfel mit beschrifteten Ecken A bis H.

Abb. 1

Zeichne in die Abbildung die Koordinatenachsen ein und bezeichne diese. Gib die Koordinaten des Punkts $A$ an.

(2P)

Der Punkt $P$ liegt auf der Kante $[FB]$ des Würfels und hat vom Punkt $H$ den Abstand $3$ . Berechne die Koordinaten des Punkts $P$ .

(3P)

Gegeben sind die Punkte $A(-2\mid 1\mid 4)$ und $B(-4\mid 0\mid 6)$ .

Bestimme die Koordinaten des Punkts $C$ so, dass gilt: $\overrightarrow{CA}= 2\cdot \overrightarrow{AB}$ .

(2P)

Durch die Punkte $A$ und $B$ verläuft die Gerade $g$ .
Betrachtet werden Geraden, für welche die Bedingungen $\text{I}$ und $\text{II}$ gelten:

$\text{I}$	Jede dieser Geraden schneidet die Gerade $g$ orthogonal.
$\text{II}$	Der Abstand jeder dieser Geraden vom Punkt $A$ beträgt $3$ .

Ermittle eine Gleichung für eine dieser Geraden.

(3P)

(10P)

Aufgabengruppe 2

Gegeben sind die Ebene $E:2x_1 + x_2 + 2x_3=6$ sowie die Punkte $P(1\mid 0\mid 2)$ und $Q(5 \mid 2 \mid 6)$ .

Zeige, dass die Gerade durch die Punkte $P$ und $Q$ senkrecht zur Ebene $E$ verläuft.

(2P)

Die Punkte $P$ und $Q$ liegen symmetrisch zu einer Ebene $F$ . Ermittle eine Gleichung von $F$ .

(3P)

Gegeben sind die Punkte $A(-2\mid 1\mid 4)$ und $B(-4\mid 0\mid 6)$ .

Bestimme die Koordinaten des Punkts $C$ so, dass gilt: $\overrightarrow{CA}= 2\cdot \overrightarrow{AB}$ .

(2P)

Durch die Punkte $A$ und $B$ verläuft die Gerade $g$ .
Betrachtet werden Geraden, für welche die Bedingungen $\text{I}$ und $\text{II}$ gelten:

$\text{I}$	Jede dieser Geraden schneidet die Gerade $g$ orthogonal.
$\text{II}$	Der Abstand jeder dieser Geraden vom Punkt $A$ beträgt $3$ .

Ermittle eine Gleichung für eine dieser Geraden.

(3P)

(10P)

Bildnachweise [nach oben]

[1]

Aufgabengruppe 1

$\blacktriangleright$ Abbildung einzeichnen und Koordinaten von $A$ bestimmen

Der Punkt $H$ hat die Koordinaten $(0 \mid 0 \mid 0)$ , d.h. der Ursprung des Koordinatensystems liegt in $H$ . Da der Punkt $E$ als erste Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die $x$ -Achse die Gerade $EH$ . Die Richtung der $x$ -Achse ist dabei die Richtung des Vektors $\overrightarrow{HE}$ . Das Vorgehen bei der $y$ -Achse ist analog. Da der Punkt $G$ als zweite Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die $y$ -Achse die Gerade $GH$ . Die Richtung der $y$ -Achse ist dabei die Richtung des Vektors $\overrightarrow{HG}$ . Der Punkt $D$ hat als letzte Koordinate eine negative Zahl (die restlichen Koordinaten sind gleich Null), das bedeutet, dass die $z$ -Achse die Gerade $DH$ ist. Die Richtung ist dieses Mal allerdings die Richtung des Vektors $\overrightarrow{DH}$ .

Somit ergibt sich folgendes Koordinatensystem:

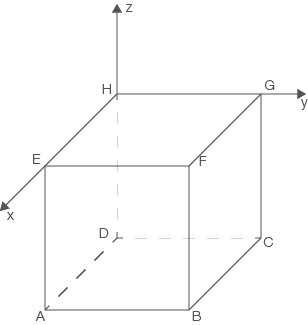3D-Darstellung eines Würfels mit Achsenbeschriftungen x, y und z.

Abb. 1: Würfel im Koordinatensystem

Der Punkt $A$ hat demnach die Koordinaten $(2 \mid 0 \mid -2).$

$\blacktriangleright$ Koordinaten des Punkts $P$ bestimmen

Sind zwei Punkte $P_1(x_1 \mid y_1 \mid z_1)$ und $P_2(x_2 \mid y_2 \mid z_2)$ gegeben, so ist der Abstand $\boldsymbol{d}$ der beiden Punkte definiert als

$\boldsymbol{d = \quad ...}.$

Vollständige Lösung anzeigen

$\boldsymbol{d = \sqrt{(x_1-x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2}}.$

Der Punkt $P$ soll auf der Kante $\overline{FB}$ des Würfels liegen und soll zum Punkt $H$ (dem Ursprung des Koordinatensystems) den Abstand $3$ haben, d.h. $d=3$ . Die Koordinaten des zweiten Punkts $H$ sind gegeben. Die Koordinaten des ersten Punkts $P$ kannst du mithilfe des Ortvektors von $F$ und dem Vektor $\overrightarrow{FB}$ umschreiben.

$P = \overrightarrow{OF} + \lambda \cdot \overrightarrow{FB} = \pmatrix{2 \\ 2 \\ 0} + \lambda \cdot \pmatrix{0 \\ 0 \\ -2}$ mit $0 \leq \lambda \leq 1.$

Setze nun die Koordinaten der Punkte in die Formel für den Abstand mit $d=3$ ein und löse die Gleichung nach $\lambda$ auf

$\begin{array}[t]{rll} 3 &=& \quad ... \end{array}$

Vollständige Lösung anzeigen

Da für $\lambda = -\dfrac{1}{2}$ der Punkt $P$ nicht auf der Kante $\overline{FB}$ liegen würde, muss $\lambda = \dfrac{1}{2}$ sein. Für $\overrightarrow{OP}$ gilt somit

$\overrightarrow{OP} = \pmatrix{2 \\ 2 \\ 0} + \dfrac{1}{2} \cdot \pmatrix{0 \\ 0 \\ -2} = \pmatrix{2 \\ 2 \\ -1}.$

Somit sind die Koordinaten von $P(2 \mid 2 \mid -1).$

$\blacktriangleright$ Koordinaten des Punkts $C$ bestimmen

Gesucht ist ein Punkt $C$ , der die Bedingung $\overrightarrow{CA} = 2 \cdot \overrightarrow{AB}$ erfüllt. Du berechnest also zuerst den Vektor

$\overrightarrow{AB} = \pmatrix{-4 \\ 0 \\ 6} - \pmatrix{-2 \\ 1 \\ 4} = \pmatrix{-2 \\ -1 \\ 2}$ ,

um ihn anschließend in die Gleichung einzusetzen.

$\begin{array}[t]{rll} \pmatrix{-2 - c_1 \\ 1 - c_2 \\ 4 - c_3} &=& 2 \cdot \pmatrix{-2 \\ -1 \\ 2} \\[5pt] &=& \pmatrix{-4 \\ -2 \\ 4} \end{array}$

Somit folgt $c_1 = 2$ , $c_2 = 3$ und $c_3 = 0$ . Der gesuchte Punkt $C$ hat also die Koordinaten $(2 \mid 3 \mid 0).$

$\blacktriangleright$ Geradengleichung bestimmen

Gesucht ist eine Gerade $h$ , die die zwei Bedingungen $I$ und $II$ erfüllt. Bestimme also zuerst einen Vektor $\vec{t}$ , der die Bedingung $I$ erfüllt, um anschließend einen Aufpunkt $P$ für die Gerade $h$ auf der Geraden $g$ zu finden, der den Abstand $3$ zum Punkt $A$ hat.

1.Schritt: Vektor $\boldsymbol{\vec{t}}$ bestimmen

Der Vektor $\vec{t}$ muss orthogonal zu $\overrightarrow{AB}$ liegen, d.h. das Skalarprodukt dieser beiden Vektoren muss null sein.

$\begin{array}[t]{rll} 0 &=& \overrightarrow{AB} \circ \vec{t} \\[5pt] &=& -2t_1 - t_2 + 2t_3 \end{array}$

Wähle $t_1 = 1$ und $t_2=0$ , sodass für $t_3$ automatisch $t_3 = 1$ folgt.

Somit ist $\vec{t} = \pmatrix{1 \\ 0 \\ 1}$ und orthogonal zu $\overrightarrow{AB}$ .

2.Schritt: Aufpunkt für die Gerade $\boldsymbol{h}$ finden

Der Aufpunkt $P$ der gesuchten Gerade $h$ muss auf der Geraden $g$ liegen und den Abstand $3$ zum Punkt $A$ haben. Somit gibt es zwei mögliche Kandidaten für den Punkt $P$ , denn die Kugel mit dem Mittelpunkt $A$ und dem Radius $3$ schneidet $g$ in zwei Punkten.

Folglich muss der Richtungsvektor $\pmatrix{-2 \\ -1 \\ 2}$ vom Punkt $A$ aus $3$ Einheiten lang sein.

$\begin{array}[t]{rll} 3 &=& \left| \lambda \cdot \pmatrix{-2 \\ -1 \\ 2} \right| \\[5pt] &=& \sqrt{(-2\lambda)^2 + (-\lambda)^2 + (2\lambda)^2} \\[5pt] &=& \sqrt{9 \lambda^2} \\[5pt] &=& \pm 3 \lambda \end{array}$

Somit kann $\lambda$ entweder $1$ oder $-1$ sein.

Wähle $\lambda = 1$ und bestimme die Koordinaten von $P$ .

$\begin{array}[t]{rll} \overrightarrow{OP}&=& \overrightarrow{OA} + 1 \cdot \pmatrix{-2 \\ -1 \\ 2} \\[5pt] &=& \pmatrix{-2 \\ 1 \\ 4} + 1 \cdot \pmatrix{-2 \\ -1 \\ 2} \\[5pt] &=& \pmatrix{-4 \\ 0 \\ 6}. \end{array}$

Demnach hat $P$ die gleichen Koordinaten wie der Punkt $B$ .

3.Schritt: Geradengleichung aufstellen

Nun hast du alle notwendigen Informationen berechnet, um die Geradengleichung von $h$ aufzustellen. Du benutzt als Aufpunkt den Punkt $P$ und als Richtungsvektor $\overrightarrow{t}$ .

$h:$ $\pmatrix{-4 \\ 0 \\ 6}+ \lambda \cdot \pmatrix{1 \\ 0 \\ 1}$

Bemerkung: Beachte, dass es hier unendlich viele Lösungen gibt. Du kannst den Richtungsvektor der Gerade $h$ auch anders wählen und für den Aufpunkt $P$ gibt es zwei Möglichkeiten.

Aufgabengruppe 2

$\blacktriangleright$ Senkrechte Lage von Gerade zur Ebene $E$ zeigen

Du musst in dieser Aufgabe zeigen, dass die Gerade, die durch die Punkte $P$ und $Q$ geht, orthogonal zur Ebene $E$ ist. Da die Ebenengleichung in Koordinatenform angegeben ist, ist die einfachste Möglichkeit, den Normalenvektor an der Koordinatenform abzulesen und zeigen, dass dieser Vektor mit dem Vektor $\overrightarrow{PQ}$ linear abhängig ist.

Wenn du eine Ebene mit der Koordinatenform $ax_1 + bx_2 + cx_3 = d$ gegeben hast, lautet der Normalenvektor $\overrightarrow{n}$

$\overrightarrow{n} = \pmatrix{a \\ b \\ c}.$

Folglich lautet der Normalenvektor $\overrightarrow{n}$ der gegebenen Ebene $\overrightarrow{n} = \pmatrix{2 \\ 1 \\ 2}.$

Im nächsten Schritt berechnest du den Vektor $\overrightarrow{PQ}.$

$\begin{array}[t]{rll} \overrightarrow{PQ} &=& \overrightarrow{OQ} - \overrightarrow{OP} \\[5pt] &=& \pmatrix{5 \\ 2 \\ 6} - \pmatrix{1 \\ 0 \\ 2} \\[5pt] &=& \pmatrix{4 \\ 2 \\ 4}. \end{array}$

Die beiden Vektoren $\overrightarrow{n}$ und $\overrightarrow{PQ}$ sind linear abhängig, da $2 \cdot \pmatrix{2 \\ 1 \\ 2} = \pmatrix{4 \\ 2 \\ 4}$ .

Somit steht die Ebene $E$ senkrecht zur Geraden $PQ$ .

$\blacktriangleright$ Ebenengleichung für $F$ bestimmen

Die Punkte $P$ und $Q$ liegen symmetrisch zur Ebene $F$ , d.h. der Vektor $\overrightarrow{PQ}$ ist ein Normalenvektor der Ebene $F$ . Somit lautet die Koordinatenform der Ebene $F:$ $4x_1 + 2x_2 + 4x_3 = d$ .

Um nun das fehlende $d$ zu bestimmen, musst du die Koordinaten eines Punkt der Ebene $F$ in die Koordinatenform einsetzen.

Da $P$ und $Q$ symmetrisch zur Ebene $F$ sind, liegt der Mittelpunkt $M$ der Strecke $\overline{PQ}$ in der Ebene $F$ . Der Ortsvektor von $M$ ist demnach.

$\begin{array}[t]{rll} \overrightarrow{OM} &=& \overrightarrow{OP} + \dfrac{1}{2} \cdot \overrightarrow{PQ} \\[5pt] &=& \pmatrix{1 \\ 0 \\ 2} + \dfrac{1}{2} \cdot \pmatrix{4 \\ 2 \\ 4} \\[5pt] &=& \pmatrix{3 \\ 1 \\ 4}. \end{array}$

Der Punkt $M$ hat also die Koordinaten $(3 \mid\ 1 \mid\ 4).$ Setzte diese in die Koordinatenform, um das gesuchte $d$ zu bekommen.

$\begin{array}[t]{rll} d &=& 4 \cdot 3 + 2 \cdot 1 + 4 \cdot 4 \\[5pt] &=& 30. \\[5pt] \end{array}$

Die Koordinatenform der Ebene $F$ lautet also $4x_1 + 2x_2 + 4x_3 = 30$ bzw. $2x_1 + x_2 + 2x_3 = 15$ , wenn man die Gleichung durch $2$ teilt.

$\blacktriangleright$ Koordinaten des Punkts $C$ bestimmen

Gesucht ist ein Punkt $C$ , der die Bedingung $\overrightarrow{CA} = 2 \cdot \overrightarrow{AB}$ erfüllt. Du berechnest also zuerst den Vektor

$\overrightarrow{AB} = \pmatrix{-4 \\ 0 \\ 6} - \pmatrix{-2 \\ 1 \\ 4} = \pmatrix{-2 \\ -1 \\ 2}$ ,

um ihn anschließend in die Gleichung einzusetzen.

$\begin{array}[t]{rll} \pmatrix{-2 - c_1 \\ 1 - c_2 \\ 4 - c_3} &=& 2 \cdot \pmatrix{-2 \\ -1 \\ 2} \\[5pt] &=& \pmatrix{-4 \\ -2 \\ 4} \end{array}$

Somit folgt $c_1 = 2$ , $c_2 = 3$ und $c_3 = 0$ . Der gesuchte Punkt $C$ hat also die Koordinaten $(2 \mid 3 \mid 0).$

$\blacktriangleright$ Geradengleichung bestimmen

1.Schritt: Vektor $\boldsymbol{\vec{t}}$ bestimmen

Der Vektor $\vec{t}$ muss orthogonal zu $\overrightarrow{AB}$ liegen, d.h. das Skalarprodukt dieser beiden Vektoren muss null sein.

$\begin{array}[t]{rll} 0 &=& \overrightarrow{AB} \circ \vec{t} \\[5pt] &=& -2t_1 - t_2 + 2t_3 \end{array}$

Wähle $t_1 = 1$ und $t_2=0$ , sodass für $t_3$ automatisch $t_3 = 1$ folgt.

Somit ist $\vec{t} = \pmatrix{1 \\ 0 \\ 1}$ und orthogonal zu $\overrightarrow{AB}$ .

2.Schritt: Aufpunkt für die Gerade $\boldsymbol{h}$ finden

Folglich muss der Richtungsvektor $\pmatrix{-2 \\ -1 \\ 2}$ vom Punkt $A$ aus $3$ Einheiten lang sein.

Somit kann $\lambda$ entweder $1$ oder $-1$ sein.

Wähle $\lambda = 1$ und bestimme die Koordinaten von $P$ .

Demnach hat $P$ die gleichen Koordinaten wie der Punkt $B$ .

3.Schritt: Geradengleichung aufstellen

Nun hast du alle notwendigen Informationen berechnet, um die Geradengleichung von $h$ aufzustellen. Du benutzt als Aufpunkt den Punkt $P$ und als Richtungsvektor $\overrightarrow{t}$ .

$h:$ $\pmatrix{-4 \\ 0 \\ 6}+ \lambda \cdot \pmatrix{1 \\ 0 \\ 1}$

Bemerkung: Beachte, dass es hier unendlich viele Lösungen gibt. Du kannst den Richtungsvektor der Gerade $h$ auch anders wählen und für den Aufpunkt $P$ gibt es zwei Möglichkeiten.

Bildnachweise [nach oben]

[1]