Teil A
1
Gegeben ist die Funktion  mit maximaler Definitionsmenge
mit maximaler Definitionsmenge 
a)
Skizziere die Parabel mit der Gleichung  in einem Koordinatensystem und gib
in einem Koordinatensystem und gib  an.
an.
(3 BE)
b)
Ermittle den Term der Ableitungsfunktion  von
von 
(2 BE)
2
Die Abbildung 1 zeigt einen Teil des Graphen  einer in
einer in  definierten gebrochenrationalen Funktion
definierten gebrochenrationalen Funktion  .
.
Die Funktion hat bei
hat bei  eine Polstelle ohne Vorzeichenwechsel; zudem besitzt
eine Polstelle ohne Vorzeichenwechsel; zudem besitzt  die Gerade mit der Gleichung
die Gerade mit der Gleichung  als schräge Asymptote.
als schräge Asymptote.
Die Funktion
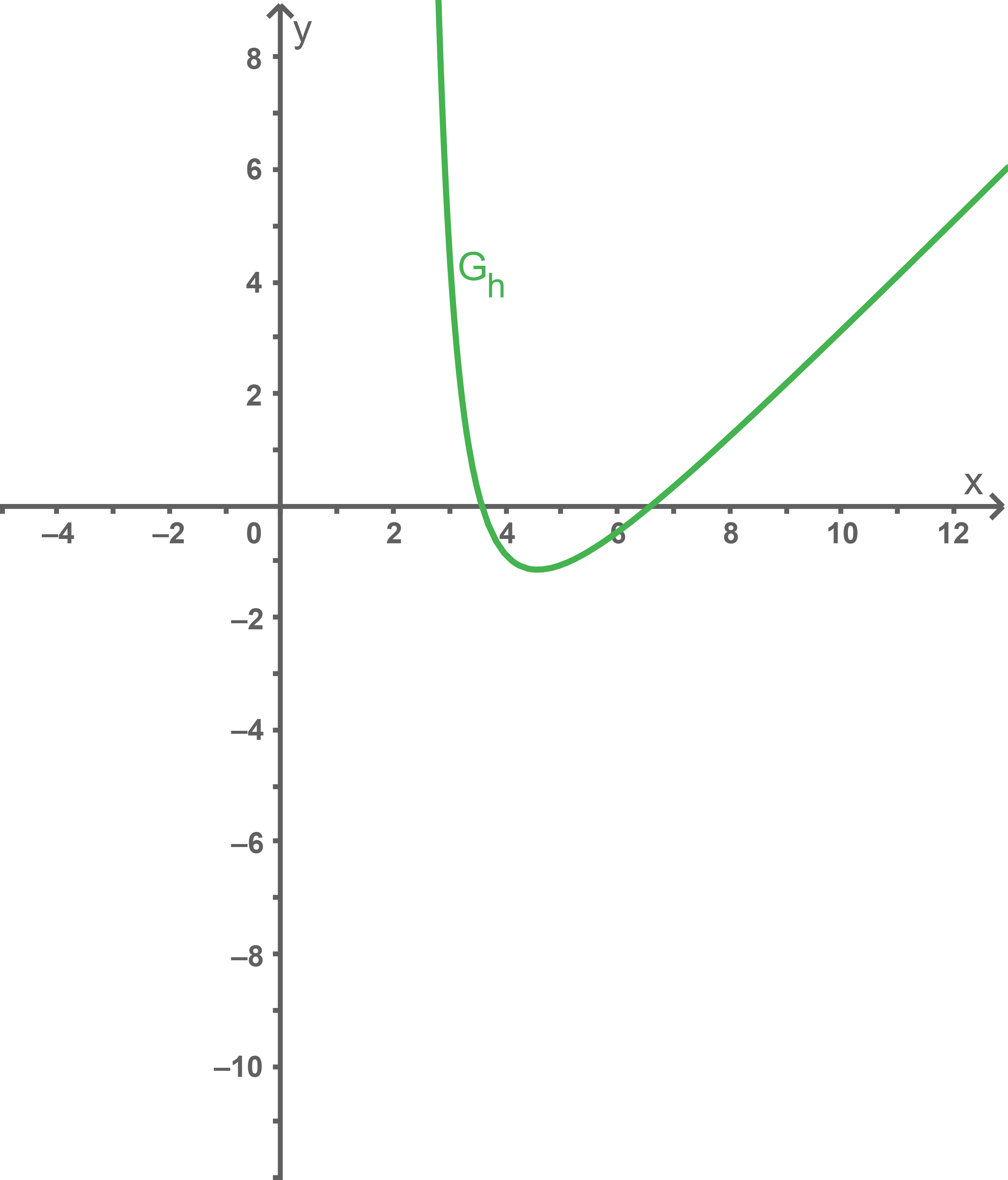
Abb. 1
a)
Zeichne in die Abbildung 1 die Asymptoten von  ein und skizziere im Bereich
ein und skizziere im Bereich  einen möglichen Verlauf von
einen möglichen Verlauf von 
(3 BE)
b)
Berechne unter Berücksichtigung des asymptotischen Verhaltens von  einen Näherungswert für
einen Näherungswert für 
(2 BE)
3
Gegeben ist die in  definierte Funktion
definierte Funktion  Ihr Graph wird mit
Ihr Graph wird mit  bezeichnet.
bezeichnet.
a)
Gib die Nullstellen von  an und begründe anhand des Funktionsterms, dass
an und begründe anhand des Funktionsterms, dass  die Gerade mit der Gleichung
die Gerade mit der Gleichung  als waagrechte Asymptote besitzt.
als waagrechte Asymptote besitzt.
(3 BE)
b)
Berechne die  -Koordinate des Schnittpunkts von
-Koordinate des Schnittpunkts von  mit der waagrechten Asymptote.
mit der waagrechten Asymptote.
(2 BE)
4
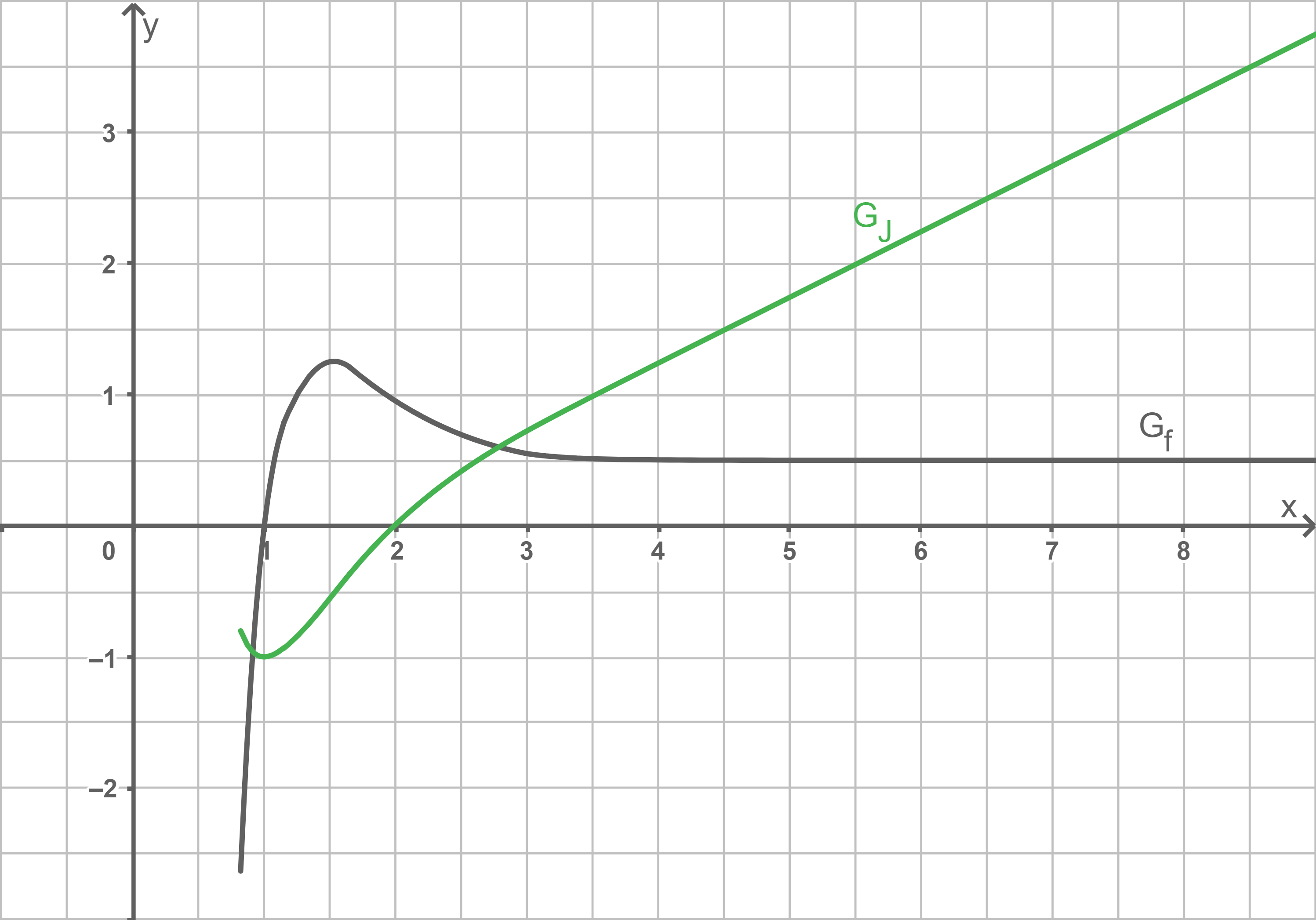
Die Abbildung 2 zeigt den Graphen  einer in
einer in  definierten Funktion
definierten Funktion  .
.
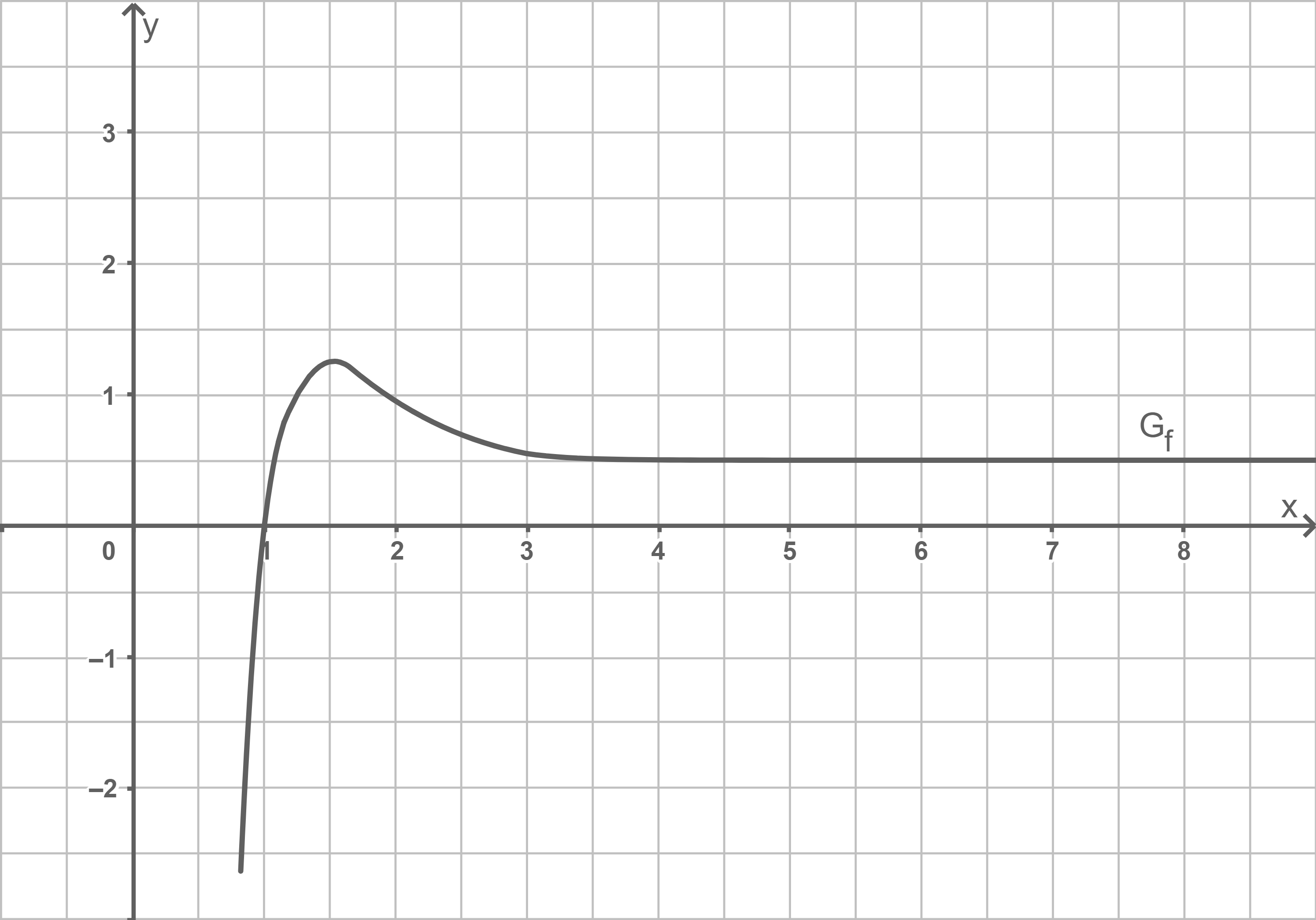 Betrachtet wird zudem die in
Betrachtet wird zudem die in  definierte Integralfunktion
definierte Integralfunktion

Begründe mithilfe von Abbildung 2, dass gilt, und gib einen Näherungswert für den Funktionswert
gilt, und gib einen Näherungswert für den Funktionswert  an. Skizziere den Graphen von
an. Skizziere den Graphen von  in der Abbildung 2.
in der Abbildung 2.

Abb. 2
Begründe mithilfe von Abbildung 2, dass
(5 BE)
(20 BE)
1
a)
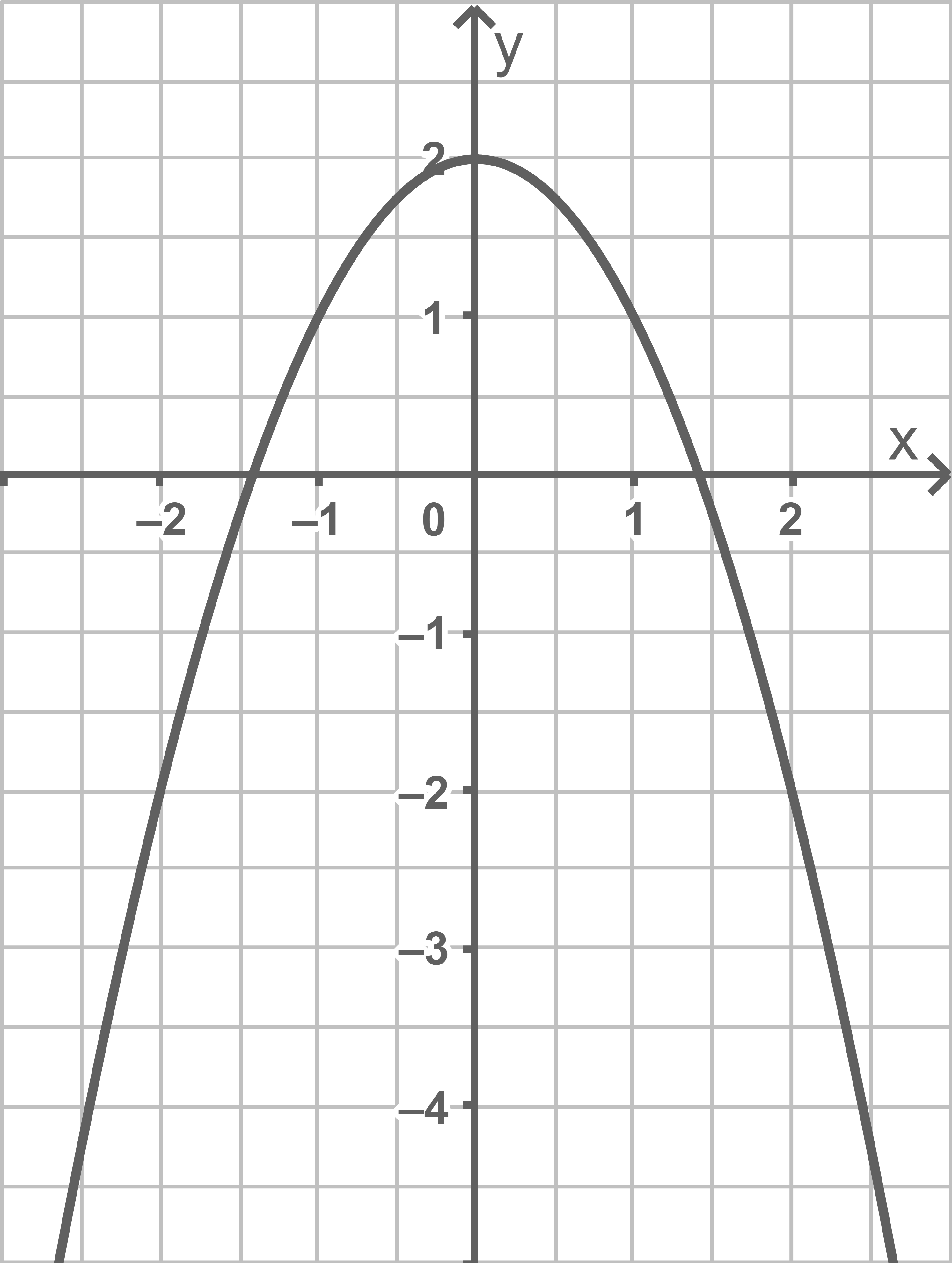
b)
Mit der Kettenregel folgt:

2
a)
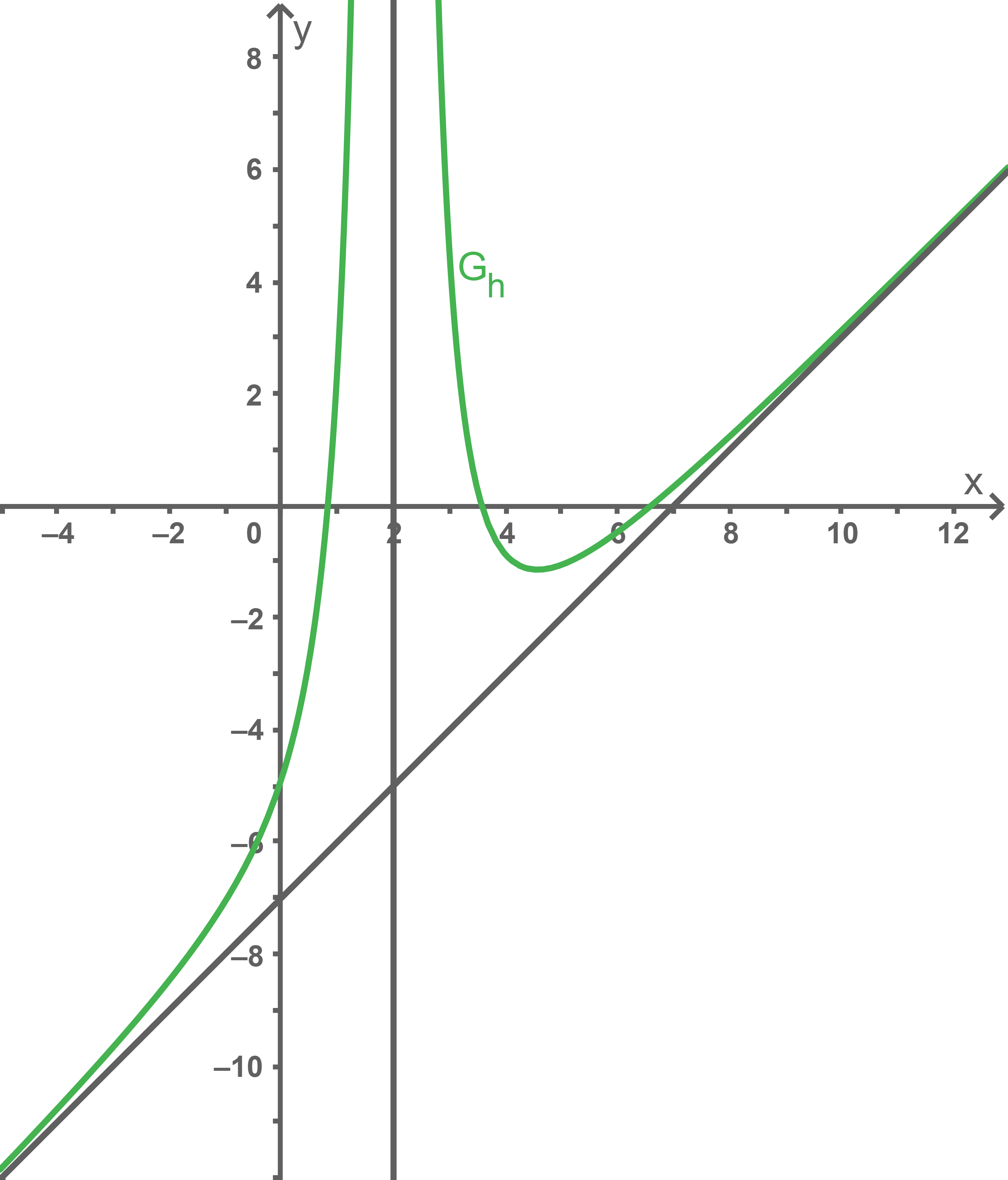
b)
3
a)
Nullstellen angeben
Der Zähler  von
von  nimmt für
nimmt für  und für
und für  den Wert Null an. Da der Nenner der Funktion für diese beiden Werte nicht Null wird, sind
den Wert Null an. Da der Nenner der Funktion für diese beiden Werte nicht Null wird, sind  und
und  die Nullstellen von
die Nullstellen von  Asymptote begründen
Da der Zählergrad und Nennergrad gleich sind, besitzt
Asymptote begründen
Da der Zählergrad und Nennergrad gleich sind, besitzt  eine waagrechte Asymptote. Mit Hilfe von
eine waagrechte Asymptote. Mit Hilfe von  ergibt sich die Gleichung dieser Asymptote als
ergibt sich die Gleichung dieser Asymptote als 
b)
4
Die Abbildung liefert, dass  zwischen
zwischen  und
und  ca. vier Kästchen mit der
ca. vier Kästchen mit der  -Achse einschließt. Vier Kästchen entsprechen hierbei
-Achse einschließt. Vier Kästchen entsprechen hierbei  Da die untere Grenze des Integrals größer ist als die obere, folgt insgesamt
Da die untere Grenze des Integrals größer ist als die obere, folgt insgesamt 
Zwischen und
und  schließt
schließt  ca. 6 Kästchen mit der
ca. 6 Kästchen mit der  -Achse ein. Da vier Kästchen
-Achse ein. Da vier Kästchen  entsprechen, folgt somit
entsprechen, folgt somit 
Mit Hilfe dieser Werte folgt für den Graphen der Integralfunktion
der Integralfunktion 
Zwischen
Mit Hilfe dieser Werte folgt für den Graphen
