Teil B
Die SMV eines Gymnasiums initiierte im vergangenen Schuljahr die Aktionen "Baumpatenschaft" und "Umweltwoche".
1
Mit einer Umfrage auf dem Schulfest wird der Bekanntheitsgrad der beiden Aktionen ermittelt. Von den Befragten kennt jeder Fünfte die Aktion "Baumpatenschaft".  der Befragten kennen keine der beiden Aktionen; die Aktion "Umweltwoche" kennen
der Befragten kennen keine der beiden Aktionen; die Aktion "Umweltwoche" kennen  der Befragten nicht.
der Befragten nicht.
Aus den Befragten wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse: "Die Person kennt die Aktion 'Baumpatenschaft'."
"Die Person kennt die Aktion 'Baumpatenschaft'."
 "Die Person kennt die Aktion 'Umweltwoche'."
"Die Person kennt die Aktion 'Umweltwoche'."
Aus den Befragten wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:
a)
Weise nach, dass die Ereignisse  und
und  stochastisch unabhängig sind.
stochastisch unabhängig sind.
(4 BE)
b)
Gib für den Fall, dass die ausgewählte Person die Aktion "Baumpatenschaft" kennt, die Wahrscheinlichkeit dafür an, dass sie die Aktion "Umweltwoche" nicht kennt.
(1 BE)
2
Um Geld für die beiden Aktionen einzunehmen, bietet die SMV auf dem Schulfest das Spiel "2022" an. Bei dem Spiel werden zwei Glücksräder mit drei bzw. vier gleich großen Sektoren verwendet, die wie in Abbildung 1 beschriftet sind. Für einen Einsatz von  darf man jedes der beiden Glücksräder einmal drehen. Für jede Ziffer
darf man jedes der beiden Glücksräder einmal drehen. Für jede Ziffer  die auf den erzielten Sektoren steht, werden
die auf den erzielten Sektoren steht, werden  ausbezahlt. Die Zufallsgröße
ausbezahlt. Die Zufallsgröße  beschreibt, wie oft die Ziffer
beschreibt, wie oft die Ziffer  auf den erzielten Sektoren insgesamt vorkommt.
auf den erzielten Sektoren insgesamt vorkommt.
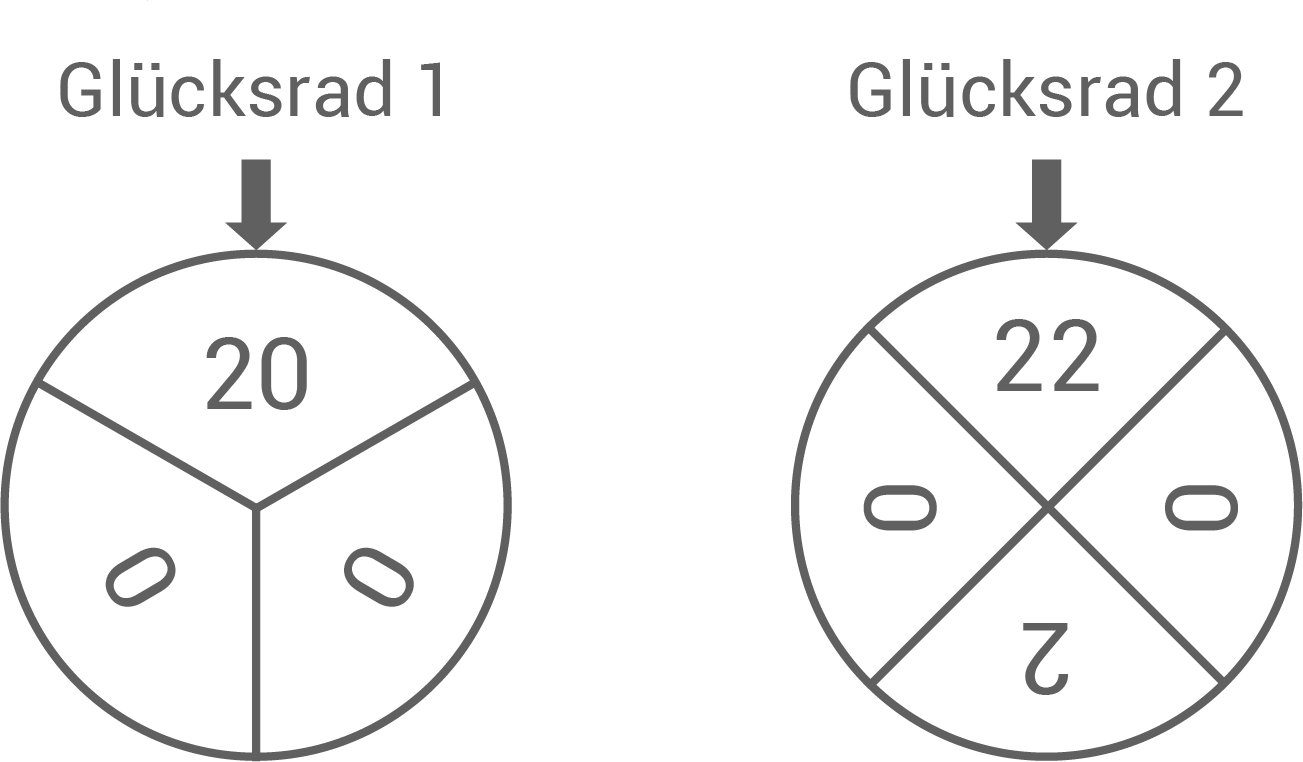

Abb. 1
a)
Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von  Bestimme die Wahrscheinlichkeiten
Bestimme die Wahrscheinlichkeiten  und
und 
 Zur Kontrolle:
Zur Kontrolle: ![\(p_2= \dfrac{1}{4} \bigg]\)](https://mathjax.schullv.de/6c4f68c4698dc7920ac4f97cadc7e1b541435dafce1e7c13318e9770c635ed1d?color=5a5a5a)
(3 BE)
b)
Ermittle, wie viele Spiele durchgeführt werden müssen, damit der Erwartungswert der Einnahme für die beiden Aktionen  beträgt.
beträgt.
Acht Personen spielen nacheinander jeweils einmal das Spiel "2022".
(4 BE)
c)
Berechne die Wahrscheinlichkeit dafür, dass die SMV mehr als zweimal mindestens  ausbezahlen muss.
ausbezahlen muss.
(4 BE)
d)
Ermittle die Wahrscheinlichkeit dafür, dass an die ersten drei Personen insgesamt  ausbezahlt werden.
ausbezahlt werden.
(4 BE)
3
Die binomialverteilte Zufallsgröße  mit den Parametern
mit den Parametern  und
und  besitzt die Standardabweichung
besitzt die Standardabweichung  In Abbildung 2 ist die Wahrscheinlichkeitsverteilung von
In Abbildung 2 ist die Wahrscheinlichkeitsverteilung von  dargestellt.
dargestellt.
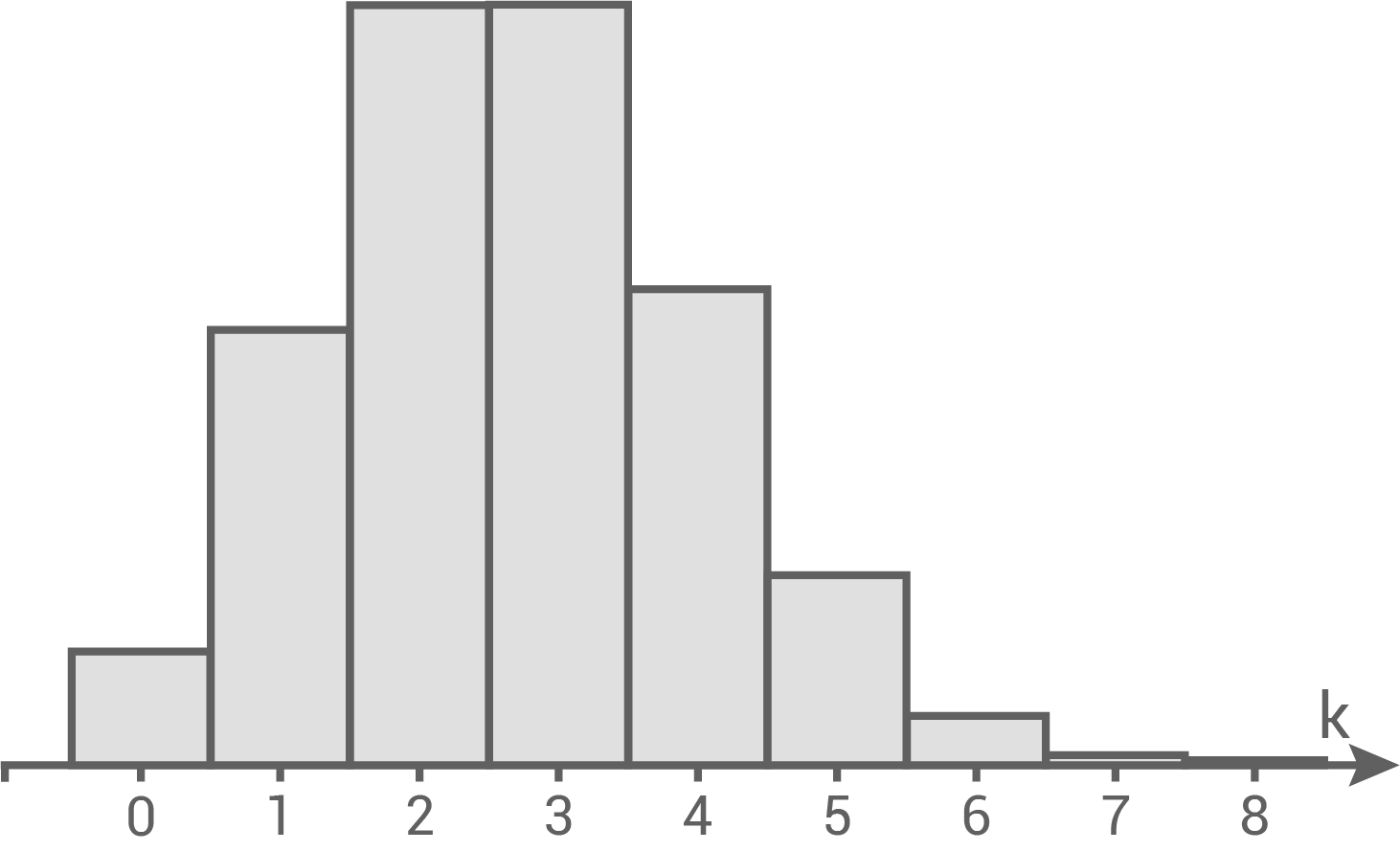

Abb. 2
a)
Ermittle mithilfe einer Rechnung den Wert des Parameters 
(3 BE)
b)
Die binomialverteilte Zufallsgröße  hat die Parameter
hat die Parameter  und
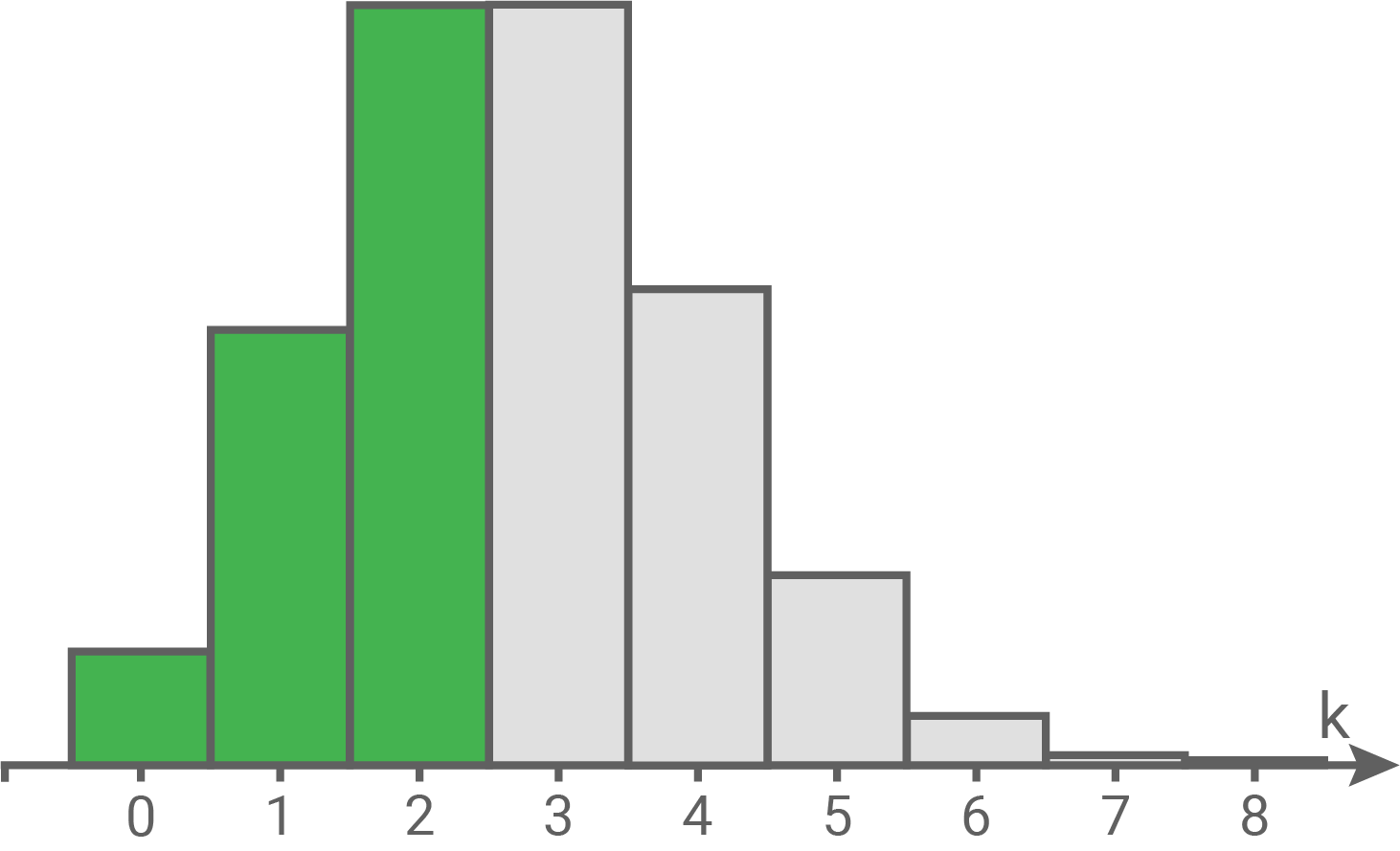
und  Kennzeichne in Abbildung 2 eine Fläche, die die Wahrscheinlichkeit
Kennzeichne in Abbildung 2 eine Fläche, die die Wahrscheinlichkeit  darstellt.
darstellt.
(2 BE)
(25 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
Da die Ereignisse  und
und  stochastisch unabhängig sind, gilt:
stochastisch unabhängig sind, gilt:
![\(\begin{array}[t]{rll}
P_B(\overline{U}) &=& P(\overline{U}) \\[5pt]
&=& 0,3 \\[5pt]
&=& 30\;\text{%}
\end{array}\)](https://mathjax.schullv.de/701d0f27583e54e995149c6274c1b8387a471f82f5dcc1b7983a24be4d443d75?color=5a5a5a)
2
a)
b)
Erwartungswert bei einem Spiel:
Somit ist die Anzahl an nötigen Spielen  für einen Erwartungswert von
für einen Erwartungswert von 
![\(\begin{array}[t]{rll}
n &=& \dfrac{300}{\dfrac{5}{6}} \\[5pt]
&=& 360
\end{array}\)](https://mathjax.schullv.de/e2346523e920bf551f41bc3f86a2ce640981a4465c846ecb84e40d7f0a6117f7?color=5a5a5a)
c)
Gegeben ist die Binomialverteilung mit den Parametern  und
und 
![\(\begin{array}[t]{rll}
P_{8;\frac{1}{3}}(X \gt 2)&=& 1 - P_{8;\frac{1}{3}}(X \leq 2) \\[5pt]
&=& 1 - 0,4682 \\[5pt]
&=& 0,5318 \\[5pt]
&=& 53,18\;\text{%}
\end{array}\)](https://mathjax.schullv.de/56764fd12aa2e33b746bf88a215865ee6bba1d4e7eaf1d626415fa3468b8311e?color=5a5a5a)
d)
Die Summe  ergibt sich durch Auszahlung von
ergibt sich durch Auszahlung von 
 und
und  Es gibt 3! Möglichkeiten, woraus folgt:
Es gibt 3! Möglichkeiten, woraus folgt:
![\(\begin{array}[t]{rll}
P &=& 3! \cdot \left( \dfrac{1}{3} \cdot \dfrac{1}{4} \cdot \dfrac{1}{12} \right) \\[5 pt]
&=& \dfrac{1}{24} \\[5 pt]
&=& 4,2 \; \%
\end{array}\)](https://mathjax.schullv.de/ed8af39bb837c44150577b926956e4157815b8eaa81cd4f2c5ab3d625e262509?color=5a5a5a)
3
a)
Es gilt:
![\(\begin{array}[t]{rll}
\sigma &=& \dfrac{4}{3} \\[5pt]
\sqrt{n \cdot p_X \cdot (1-p_X)} &=& \dfrac{4}{3} \\[5pt]
\sqrt{8 \cdot p_X \cdot (1-p_X)} &=& \dfrac{4}{3} &\quad \scriptsize \mid\; {\;}^2 \\[5pt]
8 \cdot p_X \cdot (1-p_X) &=& \dfrac{16}{9} &\quad \scriptsize \mid\; :8 \\[5pt]
p_X \cdot (1-p_X) &=& \dfrac{2}{9} &\quad \scriptsize \mid\; - \dfrac{2}{9} \\[5pt]
-p_X^2 + p_X - \dfrac{2}{9}&=& 0 &\quad \scriptsize \mid\; \cdot (-1) \\[5pt]
p_X^2 - p_X + \dfrac{2}{9} &=& 0
\end{array}\)](https://mathjax.schullv.de/0a36eb319d9f4b341766182d0c11c0d2081491b320e20b438eea867a1f7bc0c4?color=5a5a5a) Mithilfe der pq-Formel ergibt sich:
Mithilfe der pq-Formel ergibt sich:
![\(\begin{array}[t]{rll}
p_{X_{1,2}}&=& \dfrac{1}{2} \pm \sqrt{\left( -\dfrac{1}{2} \right)^2 - \dfrac{2}{9}} \\[5pt]
&=& \dfrac{1}{2} \pm \dfrac{1}{6}
\end{array}\)](https://mathjax.schullv.de/7823df3f36cb106bd9b092c28fc15a562626777aa46a69e99a1bc4fede906952?color=5a5a5a)

 Aus der Abbildung lässt sich folgern:
Aus der Abbildung lässt sich folgern:
![\(\begin{array}[t]{rll}
\mu &\approx& 2,5 \\[5pt]
n \cdot p &=& 2,5 \\[5pt]
8p &=& 2,5 &\quad \scriptsize \mid\; :8 \\[5pt]
p &=& 0,3125
\end{array}\)](https://mathjax.schullv.de/eaea11171b347123054c4e39ff449ff691b88ddba734b64b6b86e6cb0516554e?color=5a5a5a) Da
Da  näher an
näher an  liegt als
liegt als  , gilt
, gilt 
b)
Bei den Zufallsgrößen  und
und  sind Treffer und Niete vertauscht.
Es folgt:
sind Treffer und Niete vertauscht.
Es folgt:
 Somit ergibt sich folgende Fläche:
Somit ergibt sich folgende Fläche: