Teil A
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung).
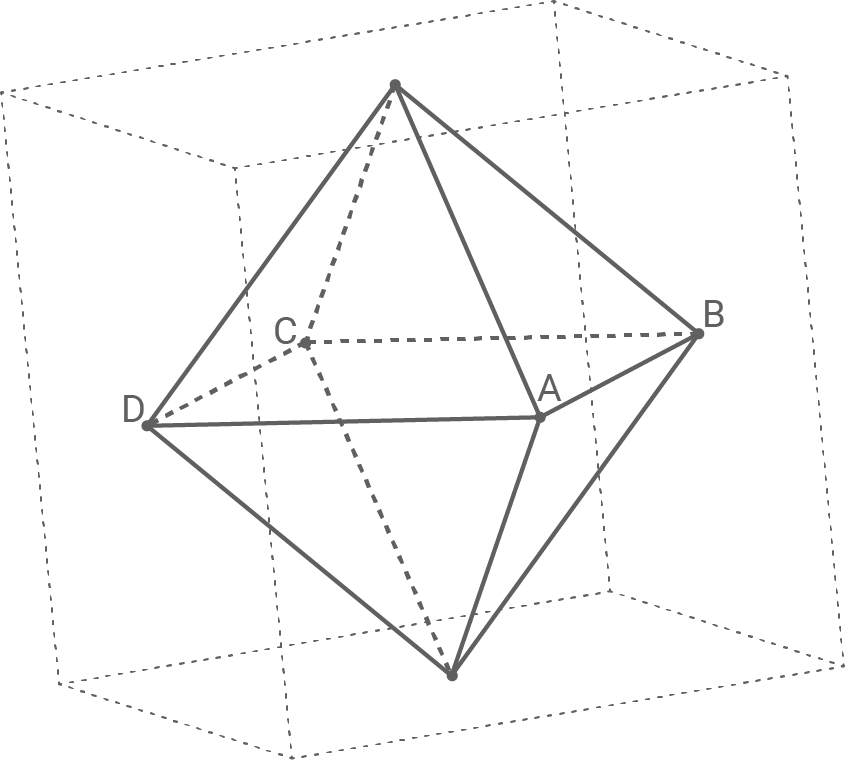Die Eckpunkte 
und 
des Oktaeders liegen in der Ebene 
mit der Gleichung 
a)
Weise nach, dass die Kantenlänge des Würfels 12 beträgt.
(2 BE)
b)
Bestimme die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in liegen.
(3 BE)
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
b)
Der Ortsvektor des Mittelpunkts 
der Strecke ![\([AC]\)](https://mathjax.schullv.de/44be0e8147732b25a3f4757d561eaef3b973da61bf19e4e02bd99aa4a8ce7f9e?color=5a5a5a)
ergibt sich wie folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt]
&=&\pmatrix{1\\2\\1}+\dfrac{1}{2}\cdot\pmatrix{-4\\-8\\8} \\[5pt]
&=&\pmatrix{-1\\-2\\5}
\end{array}\)](https://mathjax.schullv.de/f13901135af0ed1192f659481eb360c4523f0a812f6d7c78db8b4d46d714bd89?color=5a5a5a)
Aus der Ebenengleichung von lässt sich zudem der folgende Normalenvektor ablesen:
Es gilt 
Da die Kantenlänge des Würfels 
beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu durch 
gegeben. Ein möglicher Ortsvektor ergibt sich somit als:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}+2\cdot\overrightarrow{n}&=&\pmatrix{-1\\-2\\5}+2\cdot\pmatrix{2\\1\\2} \\[5pt]
&=&\pmatrix{3\\0\\9}
\end{array}\)](https://mathjax.schullv.de/04ec95577f1efba0c8c2541cc42cf6b5b46ccc1848f3bfc031c3117bb2f34c68?color=5a5a5a)
Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch 