Teil B

Der in der Abbildung 1 dargestellte Körper wird begrenzt von der quadratischen Grundfläche $ABCD$ mit $A(5\mid5\mid0),$ $B(-5\mid5\mid0),$ $C(-5\mid-5\mid0)$ und $D(5\mid-5\mid0),$ acht dreieckigen Seitenflächen und einem weiteren Quadrat $EFGH$ mit $E(2\mid0\mid4),$ $F(0\mid2\mid4),$ $G(-2\mid0\mid4)$ und $H(0\mid-2\mid4).$
Der Mittelpunkt $S$ des Quadrats $ABCD$ ist der Ursprung des Koordinatensystems und der gesamte Körper ist symmetrisch sowohl bezüglich der $x_1x_3$ -Ebene als auch bezüglich der $x_2x_3$ -Ebene.

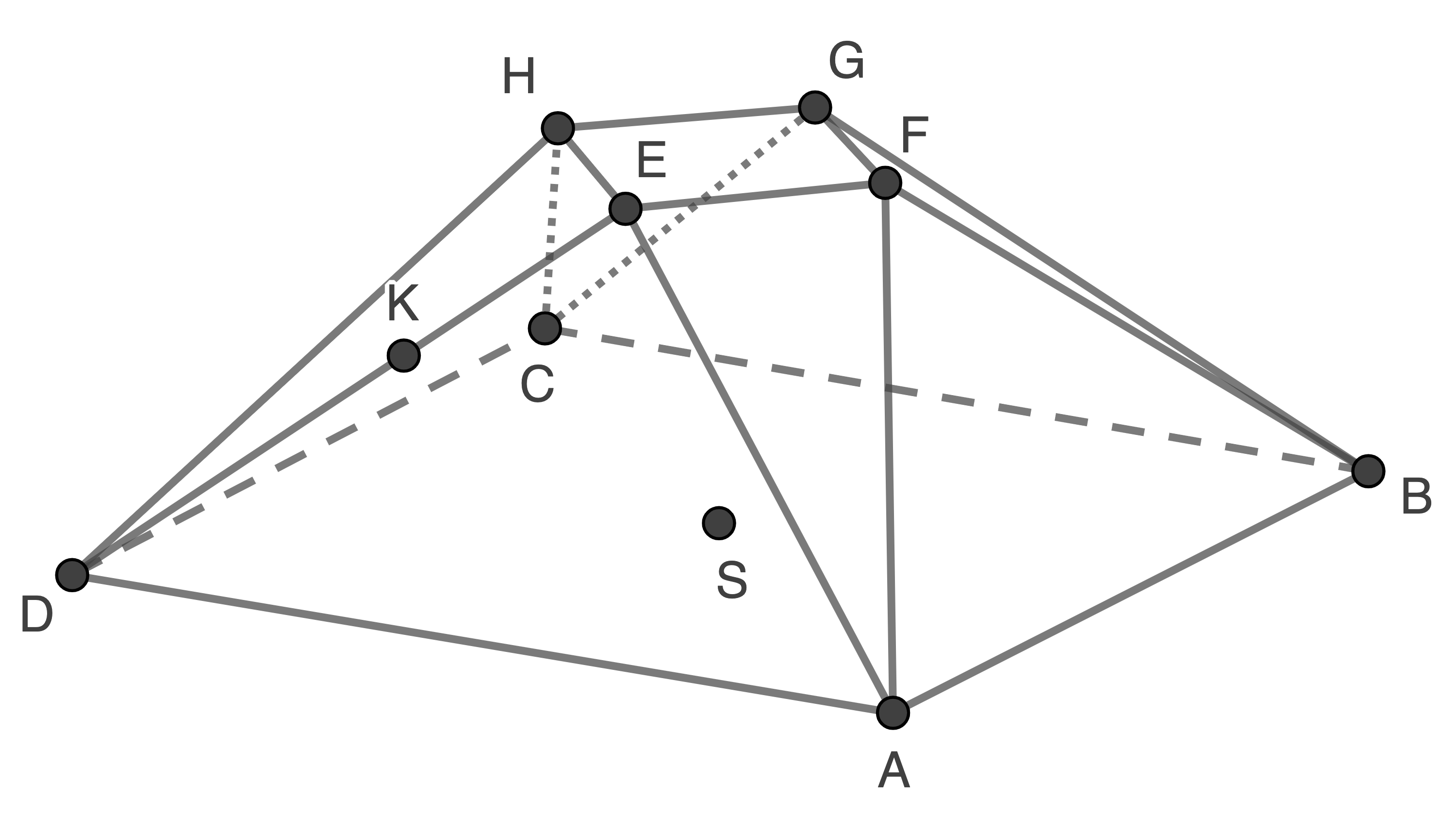
Diagramm mit Punkten und Linien, das eine geometrische Struktur darstellt.

Abb. 1

Zeige, dass das Dreieck $ABF$ bei $F$ rechtwinklig ist.

(2 BE)

Das Dreieck $ABF$ liegt in der Ebene $W$ . Ermittle eine Gleichung von $W$ in Koordinatenform und beschreibe die besondere Lage von $W$ im Koordinatensystem.

[zur Kontrolle: $W: 4x_2 +3x_3 -20 =0$ ]

(4 BE)

Berechne die Größe des spitzen Winkels, den die Seitenfläche $ABF$ und die Grundfläche $ABCD$ einschließen.

(3 BE)

Auf der Strecke $[DE]$ gibt es einen Punkt $K,$ für den $\overline{KE}= \overline{EF}$ gilt.

Bestimme die Koordinaten von $K$ .

(4 BE)

$N(1,6\mid0\mid3,2)$ ist der Mittelpunkt der Strecke $[KF].$ Begründe, dass die Gerade $EN$ den Innenwinkel des Dreiecks $DFE$ bei $E$ halbiert, und weise rechnerisch nach, dass $S$ auf der Gerade $EN$ liegt.

(4 BE)

Der Körper kann in neun Pyramiden zerlegt werden, von denen jede kongruent zu genau einer der drei Pyramiden $ABFS,$ $HDES$ bzw. $EFGHS$ ist (vgl. Abbildung 2). Die Pyramide $ABFS$ hat das Volumen $33 \frac{1}{3}$ und die Pyramide $HDES$ hat das Volumen $13 \frac{1}{3}.$ Bestimme das Volumen des gesamten Körpers.

Diagramm mit geometrischen Formen, Punkten und Linien, das eine komplexe Struktur darstellt.

Grafische Darstellung eines geometrischen Modells mit mehreren Punkten und Linien.

Abb. 2

(4 BE)

Es gibt genau eine Kugel, auf der alle acht Eckpunkte des Körpers liegen.
Ermittle die Koordinaten des Mittelpunkts dieser Kugel.

(4 BE)

(25 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\overrightarrow{FA}= \pmatrix{5\\5\\0}-\pmatrix{0\\2\\4}=\pmatrix{5\\3\\-4}$

$\overrightarrow{FB}= \pmatrix{-5\\5\\0}-\pmatrix{0\\2\\4}=\pmatrix{-5\\3\\-4}$

Rechenweg anzeigen

$\overrightarrow{FA} \circ \overrightarrow{FB} =0$

Da das Skalarprodukt von $\overrightarrow{FA}$ und $\overrightarrow{FB}$ Null ergibt, ist das Dreieck $ABF$ bei $F$ rechtwinklig.

Ebenengleichung von $\boldsymbol{W}$ ermitteln

Mit dem Kreuzprodukt folgt für ein Normalenvektor von $W:$

$\begin{array}[t]{rll} \overrightarrow{n_W}&=&\overrightarrow{FA} \times \overrightarrow{FB} \\[5pt] &=&\pmatrix{5\\3\\-4} \times \pmatrix{-5\\3\\-4} \\[5pt] &=&\pmatrix{3\cdot(-4) -(-4)\cdot 3\\ (-4)\cdot(-5) -5\cdot(-4) \\5\cdot3 -3\cdot(-5)} \\[5pt] &=&\pmatrix{0\\40\\30} \\[5pt] &=&10\cdot \pmatrix{0\\4\\3} \end{array}$

Mit dem Normalenvektor $\frac{1}{10}\cdot\overrightarrow{n_W}$ liefert Einsetzen der Koordinaten von $A:$

$\begin{array}[t]{rlll} 4x_2+3x_3 +c &=& 0 \\[5pt] 4\cdot 5+3\cdot 0 +c &=& 0 &\quad \scriptsize \mid\; -20 \\[5pt] c &=& -20 \\[5pt] \end{array}$

Somit ergibt sich eine Ebenengleichung von $W$ in Koordinatenform als $W: 4x_2+3x_3-20=0$

Lage von $\boldsymbol{W}$ beschreiben

Die $x_1$ -Koordinate des Normalenvektors $\overrightarrow{n_W}$ der Ebene ist Null, somit liegt die Ebene $W$ parallel zur $x_1$ -Achse.

Mit Hilfe des Normalenvektors $\overrightarrow{n_W}$ der Ebene $W$ und einem Normalenvektor der $x_1x_2$ -Ebene folgt für den gesuchten Winkel:

$\begin{array}[t]{rll} \cos(\alpha)&=&\dfrac{\left|\pmatrix{0\\4\\3} \circ\pmatrix{0\\0\\1} \right|}{\left|\pmatrix{0\\4\\3}\right| \cdot \left|\pmatrix{0\\0\\1} \right|} \\[5pt] \cos(\alpha)&=&\dfrac{\left| 0\cdot0 +4\cdot0 +3 \cdot 1\right|}{\sqrt{4^2+3^2} \cdot \sqrt{1^2}} \\[5pt] \cos(\alpha)&=&\dfrac{3}{5} \\[5pt] \alpha&=&\cos^{-1}\left(\dfrac{3}{5}\right) \\[5pt] \alpha&\approx&53,13^\circ \end{array}$

Um den Vektor $\overrightarrow{EK}$ zu erhalten, wird $\overrightarrow{ED}$ durch seine Länge geteilt und mit der Länge von $\overrightarrow{EF}$ multipliziert. Damit folgt:

Vollständigen Rechenweg anzeigen

$\overrightarrow{OK} = \pmatrix{3,2\\-2\\2,4}$

Die Koordinaten von $K$ lauten somit $K(3,2 \mid -2 \mid 2,4).$

Halbierung des Innenwinkels begründen

Da $\overline{EK} = \overline{EF}$ gilt, ist das Dreieck $KFE$ gleichschenklig. Der Punkt $N$ ist zudem der Mittelpunkt der Strecke $[KF],$ sodass die Gerade $EN$ den Innenwinkel des Dreiecks $KFE$ bei $E$ halbiert.
Da $K$ auf $[ED]$ liegt, entspricht der Innenwinkel des Dreiecks $KFE$ bei $E$ dem Innenwinkel des Dreiecks $DFE$ bei $E.$ Dieser wird somit von der Geraden $EN$ halbiert.

Nachweisen, dass $\boldsymbol{S}$ auf der Geraden liegt

$\overrightarrow{EN}= \pmatrix{1,6-2\\0-0\\3,2-4} = \pmatrix{-0,4\\0\\-0,8}$

Mit $\overrightarrow{EN}$ als Richtungsvektor folgt eine Gleichung der Geraden $EN:$

$EN: \overrightarrow{x}= \pmatrix{2\\0\\4} + \lambda \cdot\pmatrix{-0,4\\0\\-0,8}$

Gleichsetzen mit $S$ liefert:

$\pmatrix{0\\0\\0} = \pmatrix{2\\0\\4} + \lambda \cdot\pmatrix{-0,4\\0\\-0,8}$

Es ergibt sich folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&0&=& 2-0,4\lambda &\quad \\ \text{II}\quad&0&=&0 &\quad \\ \text{III}\quad&0&=&4-0,8\lambda &\quad \\ \end{array}$

Aus Gleichung $\text{I}$ folgt $\lambda=5.$ Einsetzen in Gleichung $\text{III}$ liefert $0=4-0,8\cdot5$ $=4-4=0.$ Somit gibt es eine eindeutige Lösung des Gleichungssystems und $S$ liegt auf der Geraden $EN.$

Der Körper besteht aus vier Pyramiden die kongruent zur Pyramide $ABFS$ sind, vier Pyramiden die kongruent zur Pyramide $HDES$ sind und der Pyramide $EFGHS.$
Die Höhe $h$ der Pyramide $EFGHS$ ergibt sich aus der $x_3$ -Koordinate der Eckpunkte des Quadrates $EFGH$ und beträgt somit $h=4.$ Damit folgt für das Volumen der Pyramide:

$V_{EFGHS}=\dfrac{1}{3} \cdot \left| \overrightarrow{EF}\right|^2 \cdot h$ $= \dfrac{1}{3} \cdot \sqrt{8}^2 \cdot 4 = \dfrac{32}{3}$

Für das Volumen $V$ des gesamten Körpers gilt somit:

Rechenweg anzeigen

$V = 197\dfrac{1}{3}\;\text{VE}$

Die allgemeinen Koordinaten des Mittelpunktes der Kugel sind $M(0 \mid 0 \mid m)$ , da der Körper symmetrisch zur $x_1x_3$ -Ebene und zur $x_2x_3$ -Ebene liegt und der Mittelpunkt somit auf der $x_3$ -Achse liegt.
Da alle Eckpunkte des Körpers auf der Kugel liegen sollen, müssen diese auch denselben Abstand zum Mittelpunkt $M$ auf der $x_3$ -Achse haben. Dieser Abstand entspricht dem Radius der Kugel. Für den Verbindungsvektor des Mittelpunkts $M$ mit beispielsweise $A$ und $F$ folgt:

$\overrightarrow{MA}= \pmatrix{5-0\\5-0\\0-m}=\pmatrix{5\\5\\-m}$

$\overrightarrow{MF}= \pmatrix{0-0\\2-0\\4-m}=\pmatrix{0\\2\\4-m}$

Da der Betrag dieser beiden Vektoren gleich sein muss, folgt weiter:

$m=-3,75$

Rechenweg anzeigen

Da laut Aufgabenstellung genau eine Kugel mit der gewünschten Eigenschaft existiert und die Lösung für $m$ eindeutig ist, müssen die anderen Eckpunkte nicht mehr betrachtet werden und für die Koordinaten des Mittelpunktes der Kugel folgt $M(0 \mid0 \mid -3,75).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?