Teil B
Auf einem Abschnitt einer wenig befahrenen Landstraße ist eine Höchstgeschwindigkeit von  zugelassen. An einer Stelle dieses Abschnitts wird die Geschwindigkeit vorbeifahrender Pkw gemessen. Im Folgenden werden vereinfachend nur solche Fahrten betrachtet, bei denen die Fahrer die Geschwindigkeit unabhängig voneinander wählen konnten.
zugelassen. An einer Stelle dieses Abschnitts wird die Geschwindigkeit vorbeifahrender Pkw gemessen. Im Folgenden werden vereinfachend nur solche Fahrten betrachtet, bei denen die Fahrer die Geschwindigkeit unabhängig voneinander wählen konnten.
1
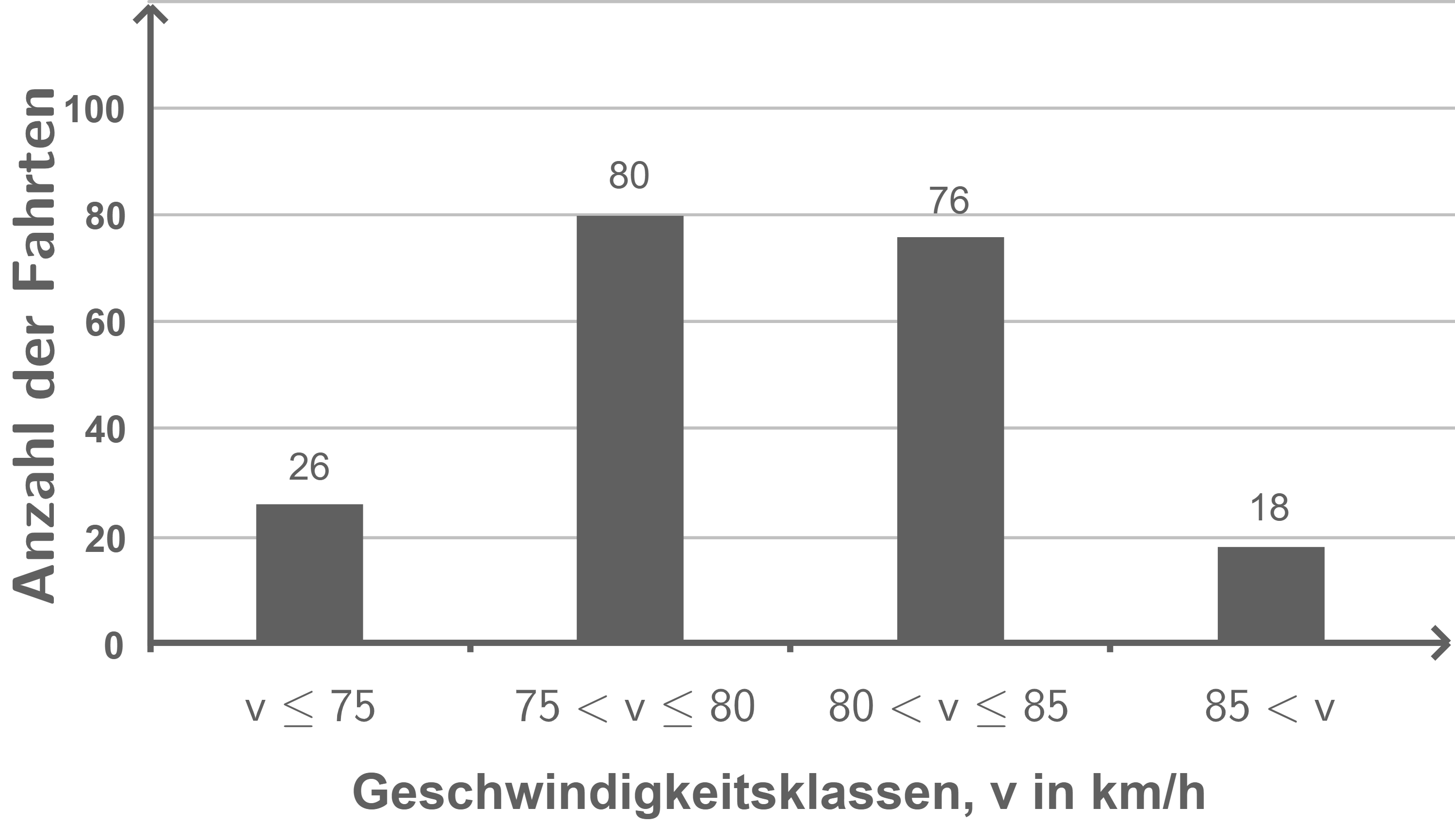
Für die ersten  erfassten Fahrten ergab sich nach Einteilung in Geschwindigkeitsklassen die folgende Verteilung:
erfassten Fahrten ergab sich nach Einteilung in Geschwindigkeitsklassen die folgende Verteilung:
 Bei
Bei  der
der  Fahrten war der Fahrer allein unterwegs,
Fahrten war der Fahrer allein unterwegs,  dieser Alleinfahrer fuhren zu schnell. Aus den
dieser Alleinfahrer fuhren zu schnell. Aus den  Fahrten wird eine zufällig ausgewählt. Es werden folgende Ereignisse betrachtet:
Fahrten wird eine zufällig ausgewählt. Es werden folgende Ereignisse betrachtet:


 genau gemessenen Geschwindigkeiten näherungsweise durch eine Binomialverteilung mit den Parametern
genau gemessenen Geschwindigkeiten näherungsweise durch eine Binomialverteilung mit den Parametern  und
und  beschrieben werden kann. Beispielsweise entspricht
beschrieben werden kann. Beispielsweise entspricht  näherungsweise dem Anteil der mit einer Geschwindigkeit von
näherungsweise dem Anteil der mit einer Geschwindigkeit von  erfassten Pkw.
erfassten Pkw.

„Der Fahrer war allein unterwegs.“
„Der Pkw war zu schnell.“
a)
Weise nach, dass die Ereignisse  und
und  stochastisch abhängig sind, und gib hierfür einen möglichen Grund im Sachzusammenhang an.
stochastisch abhängig sind, und gib hierfür einen möglichen Grund im Sachzusammenhang an.
Die Geschwindigkeitsmessungen werden über einen längeren Zeitraum fortgesetzt. Dabei zeigt sich, dass die Verteilung der auf
(5 BE)
b)
Bestätige exemplarisch für eine der beiden mittleren Geschwindigkeitsklassen der oben dargestellten Stichprobe, dass die ermittelte Anzahl der Fahrten mit der Beschreibung durch die Binomialverteilung im Einklang steht.
(4 BE)
c)
Bestimme unter Verwendung dieser Binomialverteilung die kleinste Geschwindigkeit  für die die folgende Aussage zutrifft: „Bei mehr als
für die die folgende Aussage zutrifft: „Bei mehr als  der erfassten Fahrten wird
der erfassten Fahrten wird  nicht überschritten.“
nicht überschritten.“
(2 BE)
2
Die Polizei führt an der Messstelle eine Geschwindigkeitskontrolle durch. Bei einer Geschwindigkeit von mehr als  liegt ein Tempoverstoß vor. Vereinfachend soll davon ausgegangen werden, dass die Geschwindigkeit eines vorbeifahrenden Pkw mit einer Wahrscheinlichkeit von
liegt ein Tempoverstoß vor. Vereinfachend soll davon ausgegangen werden, dass die Geschwindigkeit eines vorbeifahrenden Pkw mit einer Wahrscheinlichkeit von  größer als
größer als  ist.
ist.
a)
Berechne die Anzahl der Geschwindigkeitsmessungen, die mindestens durchgeführt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als  mindestens ein Tempoverstoß erfasst wird.
mindestens ein Tempoverstoß erfasst wird.
(4 BE)
b)
Liegt in einer Stichprobe von 50 Geschwindigkeitsmessungen die Zahl der Tempoverstöße um mehr als eine Standardabweichung unter dem Erwartungswert, geht die Polizei davon aus, dass wirksam vor der Geschwindigkeitskontrolle gewarnt wurde, und bricht die Kontrolle ab. Bestimme die Wahrscheinlichkeit dafür, dass die Geschwindigkeitskontrolle fortgeführt wird, obwohl die Wahrscheinlichkeit dafür, dass ein Tempoverstoß begangen wird, auf  gesunken ist.
gesunken ist.
(5 BE)
(20 BE)
1
a)
Aus der Aufgabenstellung und der Abbildung lassen sich folgende Wahrscheinlichkeiten ablesen:
![\(\begin{array}[t]{rll}
P(A\cap S)&=& \dfrac{65}{200} \\[5pt]
&=& 0,325 \\[5pt]
P(A)&=& 0,62 \\[5pt]
P(S)&=& \dfrac{76+18}{200} \\[5pt]
&=& 0,47
\end{array}\)](https://mathjax.schullv.de/82bb7e34d15b22902d76ca55446d33000d16c9b4da242ab8514a4a698aca2945?color=5a5a5a) Es folgt:
Es folgt:
![\(\begin{array}[t]{rll}
P(A)\cdot P(S) &=& 0,62\cdot 0,47 \\[5pt]
&=& 0,2914
\end{array}\)](https://mathjax.schullv.de/e6180d5719ea969237dd4035d9b5849459d4b2a31a8efd64b99fc2d5b0ca3ce3?color=5a5a5a) Da somit
Da somit  gilt, sind die beiden Ereignisse
gilt, sind die beiden Ereignisse  und
und  stochastisch abhängig.
stochastisch abhängig.
Ein möglicher Grund im Sachzusammenhang ist ein steigendes Verantwortungsbewusstsein des Fahrers, wenn noch andere Personen im Fahrzeug sitzen.
Ein möglicher Grund im Sachzusammenhang ist ein steigendes Verantwortungsbewusstsein des Fahrers, wenn noch andere Personen im Fahrzeug sitzen.
b)
Die Zufallsgröße  beschreibt die gemessene Geschwindigkeit eines zufällig ausgewählten Pkws auf
beschreibt die gemessene Geschwindigkeit eines zufällig ausgewählten Pkws auf  gerundet und ist binomialverteilt mit den Parametern
gerundet und ist binomialverteilt mit den Parametern  und
und  Für die Geschwindigkeitsklasse
Für die Geschwindigkeitsklasse  folgt damit:
Die Abbildung liefert, dass
folgt damit:
Die Abbildung liefert, dass  der
der  gemessenen Fahrten und somit
gemessenen Fahrten und somit  in der Geschwindigkeitsklasse
in der Geschwindigkeitsklasse  lage. Das entspricht bis auf eine geringe Abweichung der eben bestimmten Wahrscheinlichkeit, das heißt die Stichprobe steht im Einklang mit der Beschreibung durch die Binomialverteilung.
lage. Das entspricht bis auf eine geringe Abweichung der eben bestimmten Wahrscheinlichkeit, das heißt die Stichprobe steht im Einklang mit der Beschreibung durch die Binomialverteilung.
c)
Gesucht ist das kleinste  sodass folgende Ungleichung gerade noch erfüllt ist:
sodass folgende Ungleichung gerade noch erfüllt ist:
 Systematisches Ausprobieren mit dem Taschenrechner liefert:
Systematisches Ausprobieren mit dem Taschenrechner liefert:
![\(\begin{array}[t]{rll}
P(V\leq 86)&\approx& 0,9531\\[5pt]
P(V\leq 85)&\approx& 0,9196
\end{array}\)](https://mathjax.schullv.de/f6384a2dbcf453f13a2d3389830aaa7fc3e86203ca4b24470f57d9cfd534bda2?color=5a5a5a) Somit gilt
Somit gilt  das heißt bei mehr als
das heißt bei mehr als  der erfassten Fahrten wird
der erfassten Fahrten wird  nicht überschritten.
nicht überschritten.
2
a)
Die Zufallsgröße  beschreibt die Anzahl der Tempoverstöße in der Geschwindigkeitskontrolle und ist binomialverteilt mit unbekanntem
beschreibt die Anzahl der Tempoverstöße in der Geschwindigkeitskontrolle und ist binomialverteilt mit unbekanntem  und
und  Gesucht ist der kleinste Wert für
Gesucht ist der kleinste Wert für  sodass folgende Ungleichung noch erfüllt ist:
sodass folgende Ungleichung noch erfüllt ist:
 Für
Für  folgt somit:
Es müssen somit mindestens
folgt somit:
Es müssen somit mindestens  Messungen durchgeführt werden, damit mit einer Wahrscheinlichkeit von mehr als
Messungen durchgeführt werden, damit mit einer Wahrscheinlichkeit von mehr als  mindestens ein Tempoverstoß erfasst wird.
mindestens ein Tempoverstoß erfasst wird.
b)
Betrachtet wird nun die Zufallsgröße  für
für  Für den Erwartungswert und die Standardabweichung dieser Zufallsgröße ergibt sich:
Für den Erwartungswert und die Standardabweichung dieser Zufallsgröße ergibt sich:
![\(\begin{array}[t]{rll}
\mu &=& n\cdot p \\[5pt]
&=& 50 \cdot 0,19 \\[5pt]
&=& 9,5 \\[10pt]
\sigma&=&\sqrt{n\cdot p \cdot (1-p)} \\[5pt]
&=& \sqrt{9,5\cdot 0,81} \\[5pt]
&\approx& 2,77 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/072f07467670ecc9d315bb3743b3b336d718199b9ebca329a569e5abd93ec849?color=5a5a5a) Die Zufallsgröße
Die Zufallsgröße  beschreibt die Anzahl der Tempoverstöße unter den
beschreibt die Anzahl der Tempoverstöße unter den  Messungen und ist binomialverteilt mit
Messungen und ist binomialverteilt mit  und
und  Für die gesuchte Wahrscheinlichkeit folgt somit:
Für die gesuchte Wahrscheinlichkeit folgt somit:
![\(\begin{array}[t]{rll}
P(Y \geq \mu -\sigma)&=& P(Y \geq 6,73) \\[5pt]
&=& P(Y \geq 7) \\[5pt]
&=& 1-P(Y\leq 6) \\[5pt]
&\approx& 1- 0,7702 \\[5pt]
&=& 0,2298 \\[5pt]
&=& 22,98\,\%
\end{array}\)](https://mathjax.schullv.de/9b83759622f799c85df16747ee92c1bc421369c529657a4eaf4bb30cfc60f171?color=5a5a5a)