Teil A

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\mathrm{e} ^{2x+1}.$ Zeige, dass $f$ umkehrbar ist, und ermittle einen Term der Umkehrfunktion von $f$ .

(4 BE)

Gegeben ist die Funktion $g: x\mapsto (x^2-9x)\cdot \sqrt{2-x}$ mit maximaler Definitionsmenge $D_g.$
Gib $D_g$ und alle Nullstellen von $g$ an.

(3 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $h:x \mapsto \ln \,\bigg (\dfrac{1}{x^2+1}\,\bigg ).$
Begründe, dass die Wertemenge von $h$ das Intervall $]-\infty ; 0]$ ist.

(3 BE)

Betrachtet wird die in $\mathbb{R}^+$ definierte Funktion $f$ mit $f(x)=\dfrac{1}{\sqrt{x^3}}.$

Zeige, dass die in $\mathbb{R}^+$ definierte Funktion $F$ mit $F(x)=- \dfrac{2}{\sqrt x}$ eine Stammfunktion von $f$ ist.

(2 BE)

Der Graph von $f$ schließt mit der x-Achse sowie den Geraden mit den Gleichungen $x=1$ und $x=b$ mit $b>1$ ein Flächenstück ein. Bestimme denjenigen Wert von $b$ , für den dieses Flächenstück den Inhalt 1 hat.

(3 BE)

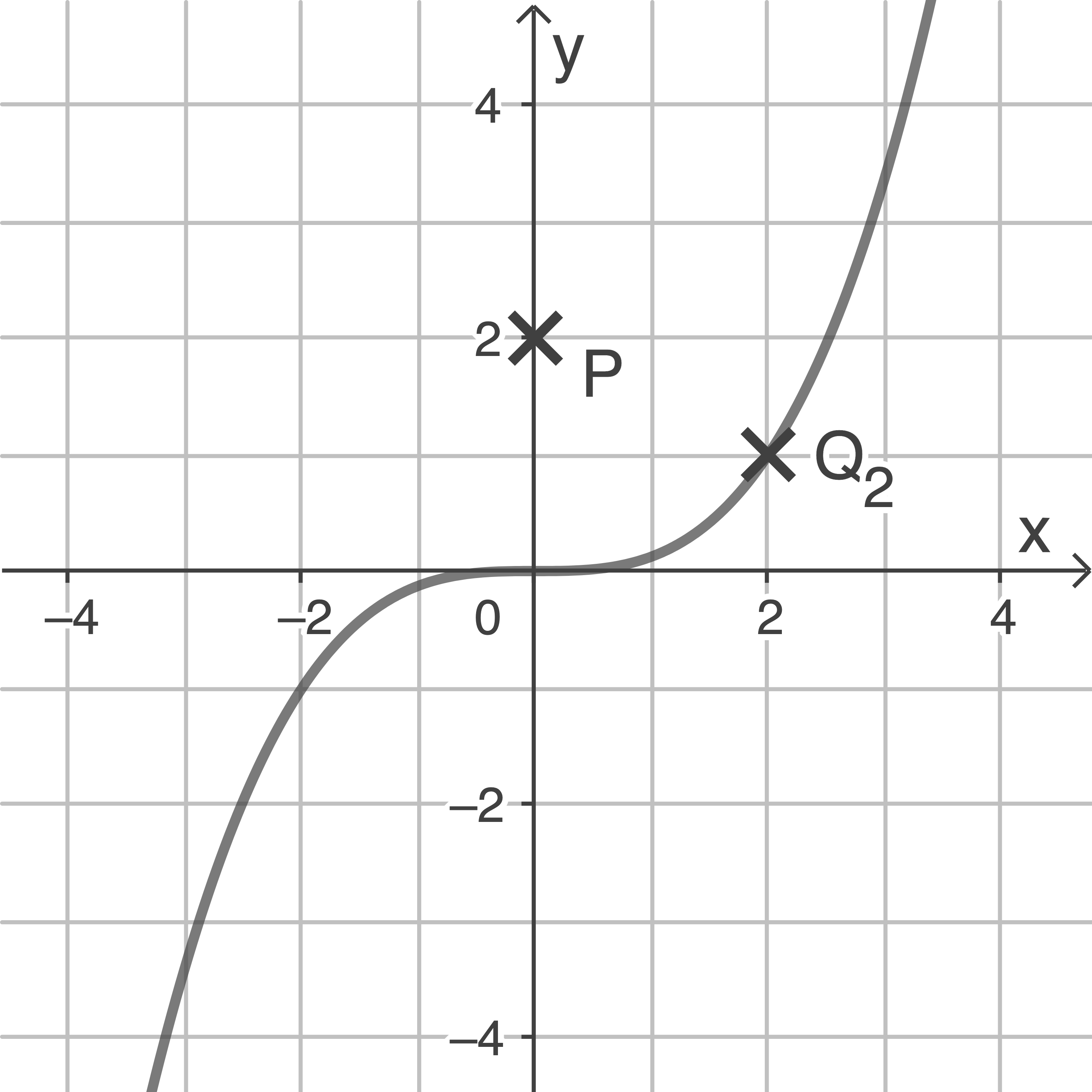
Gegeben sind die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)= \dfrac{1}{8}x^3$ sowie die Punkte $Q_a(a \mid f(a))$ für $a\in \mathbb{R}.$ Die Abbildung zeigt den Graphen von $f$ sowie die Punkte $P(0\mid 2)$ und $Q_2.$

Graph einer Funktion mit Achsen und markierten Punkten P und Q2.

Berechne für $a\neq 0$ die Steigung $m_a$ der Gerade durch die Punkte $P$ und $Q_a$ in Abbhängigkeit von $a$ .
[zur Kontrolle: $m_a= \dfrac{a^3-16}{8a}$ ]

(2 BE)

Die Tangente an den Graphen von $f$ im Punkt $Q_a$ wird mit $t_a$ bezeichnet. Bestimme rechnerisch denjenigen Wert von $a\in \mathbb{R},$ für den $t_a$ durch $P$ verläuft.

(3 BE)

(20 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?