Teil B

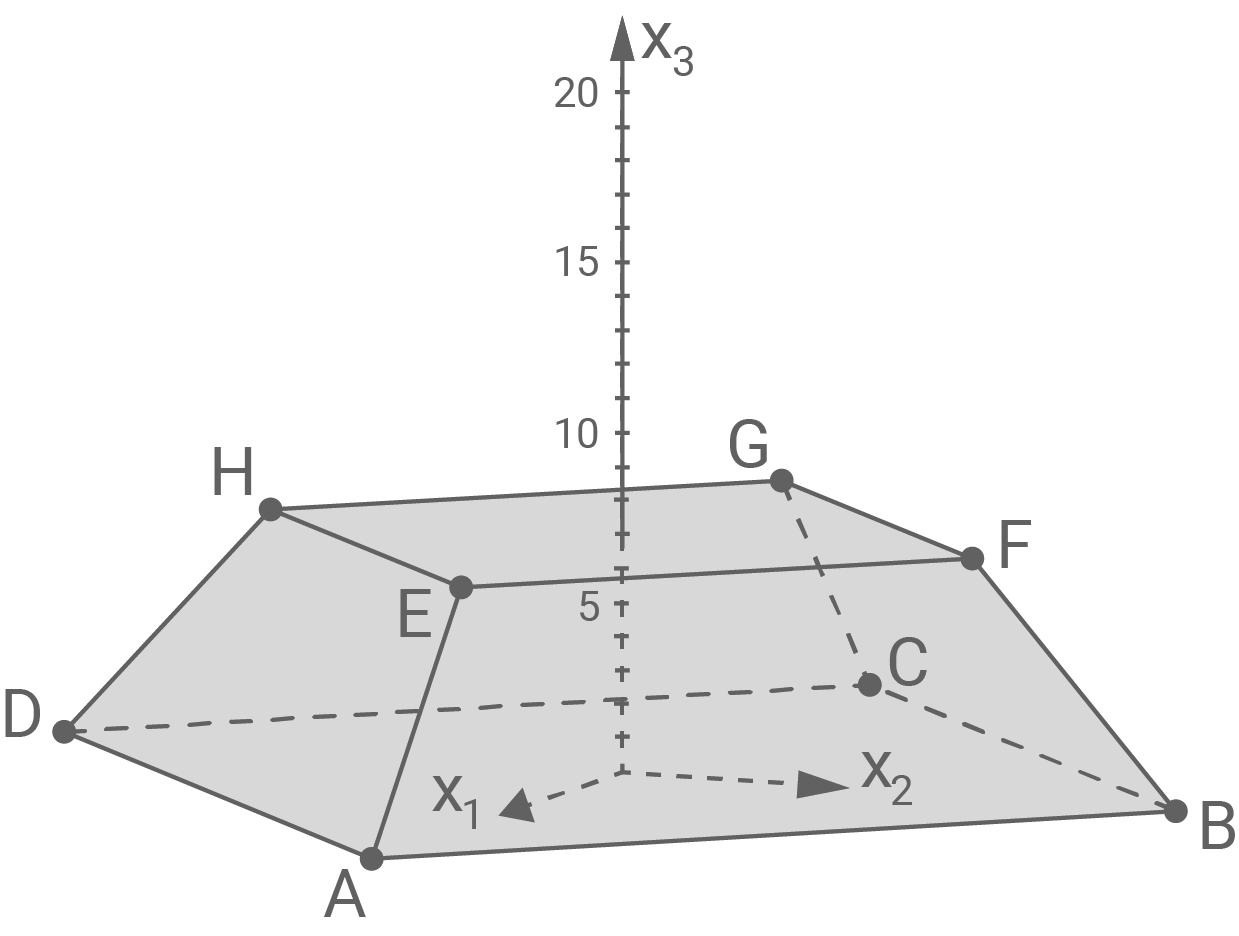
Gegeben sind die Punkte $A(19\mid0\mid 0), B(0\mid19\mid 0), E(12\mid0\mid 7)$ und $F(0\mid12\mid 7)$ (vgl. Abbildung 1). Das Viereck $ABFE$ liegt in der Ebene $L.$

Weise nach, dass das Viereck $ABFE$ ein Trapez mit zwei gleich langen Seiten ist.

(3 BE)

Bestimme eine Gleichung von $L$ in Koordinatenform sowie die Größe $\varphi$ des Winkels, den $L$ mit der $x_1x_2$ -Ebene einschließt.

(zur Kontrolle: $x_1+x_2+x_3-19=0 ; \varphi \approx 55^{\circ}$ )

(6 BE)

Abbildung 1 zeigt den Körper $ABCDEFGH,$ bei dem die quadratische Grundfläche $ABCD$ parallel zur quadratischen Deckfläche $EFGH$ liegt. Der Körper ist symmetrisch sowohl bezüglich der $x_1x_3$ -Ebene als auch bezüglich der $x_2x_3$ -Ebene. Außerdem werden die Punkte $S_k(0\mid0\mid k)$ mit $k \in]7;+\infty[$ betrachtet, die Spitzen von Pyramiden $EFGHS_k$ sind.

Abb. 1

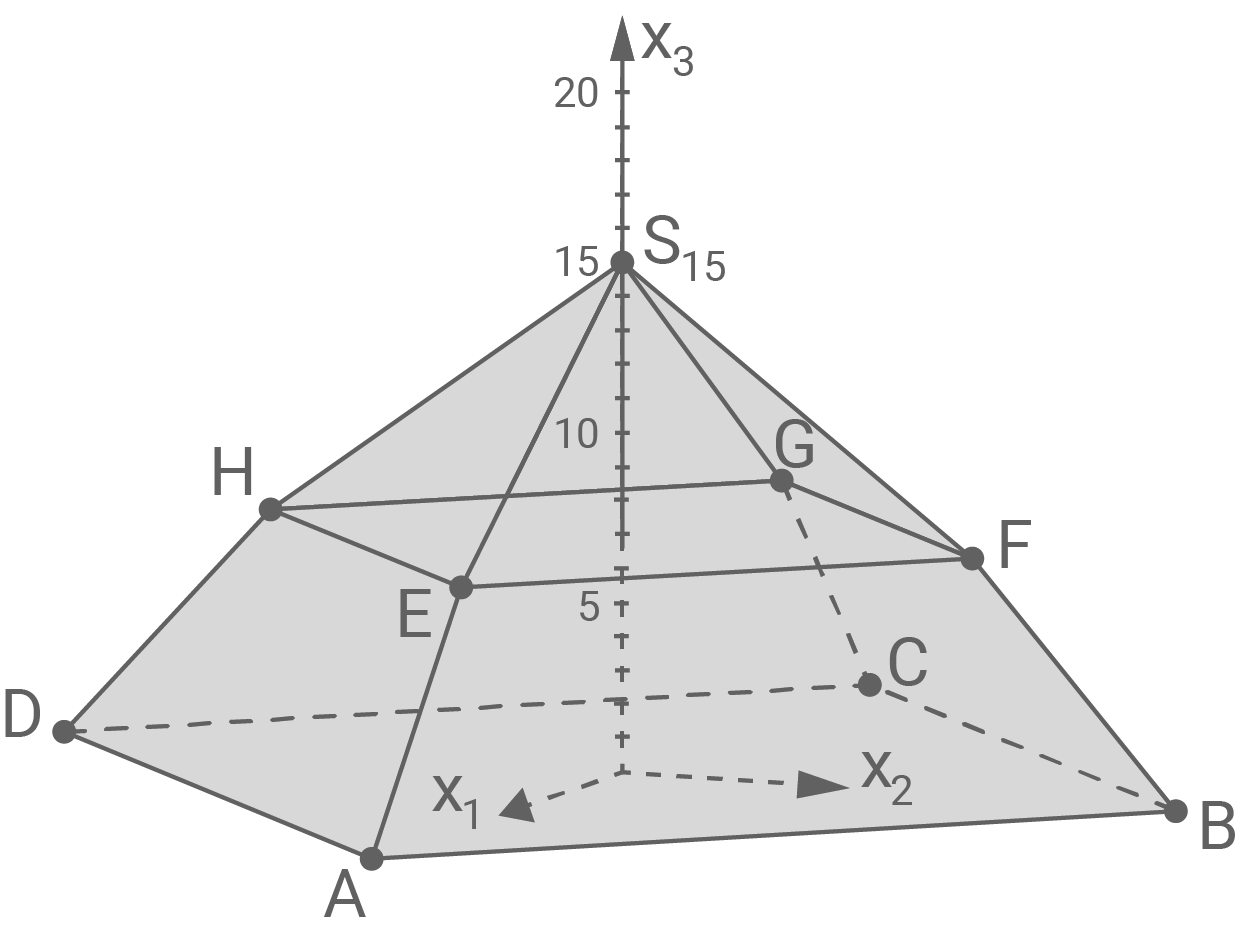
Bestimme rechnerisch denjenigen Wert von $k,$ für den die Pyramide $EFGHS_k$ den Körper $ABCDEFGH$ zu einer großen Pyramide $ABCDS_k$ ergänzt.

(zur Kontrolle: $k=19$ )

(2 BE)

Zeichne die Pyramide $EFGHS_{15}$ in Abbildung 1 ein. Die Seitenfläche $EFS_{15}$ und die Grundfläche $EFGH$ dieser Pyramide schließen einen Winkel ein. Begründe ohne weitere Rechnung, dass die Größe dieses Winkels kleiner als $45^{\circ}$ ist; verwende dazu folgende Information:
$\quad$ Für den Mittelpunkt $M$ des Quadrats $EFGH$ und den Punkt $N$ mit $\overrightarrow{N} =\frac{1}{2} \cdot(\overrightarrow{E}+\overrightarrow{F})$ gilt $\overline{MS_{15}}\lt\overline{MN}.$

(4 BE)

Der Körper $ABCDEFGHS_{15}$ stellt modellhaft die Knickpyramide des Pharaos Snofru dar, die ca. 2650 v. Chr. in Ägypten erbaut wurde (vgl. Abbildung 2). Dabei beschreibt die $x_1x_2$ -Ebene den horizontalen Boden; eine Längeneinheit im Koordinatensystem entspricht $7\;\text{m}$ in der Realität. Ursprünglich wurde mit dem Bau einer Pyramide begonnen, die im Modell der Pyramide $ABCDS_{19}$ entspricht. Aufgrund von Stabilitätsproblemen im Bauprozess musste die Neigung der Seitenflächen gegenüber dem Boden beim Erreichen einer bestimmten Höhe verändert werden. Der entstandene Knick ist namensgebend für die Pyramide.

Abb. 2

Bestimme die Höhenänderung des Bauwerks, die durch die Bauplanänderung hervorgerufen wurde, in Metern. Begründe, dass im unteren Teil des Bauwerks der Neigungswinkel der Seitenflächen gegenüber dem Boden um mehr als $9^{\circ}$ größer ist als im oberen Teil des Bauwerks.

(3 BE)

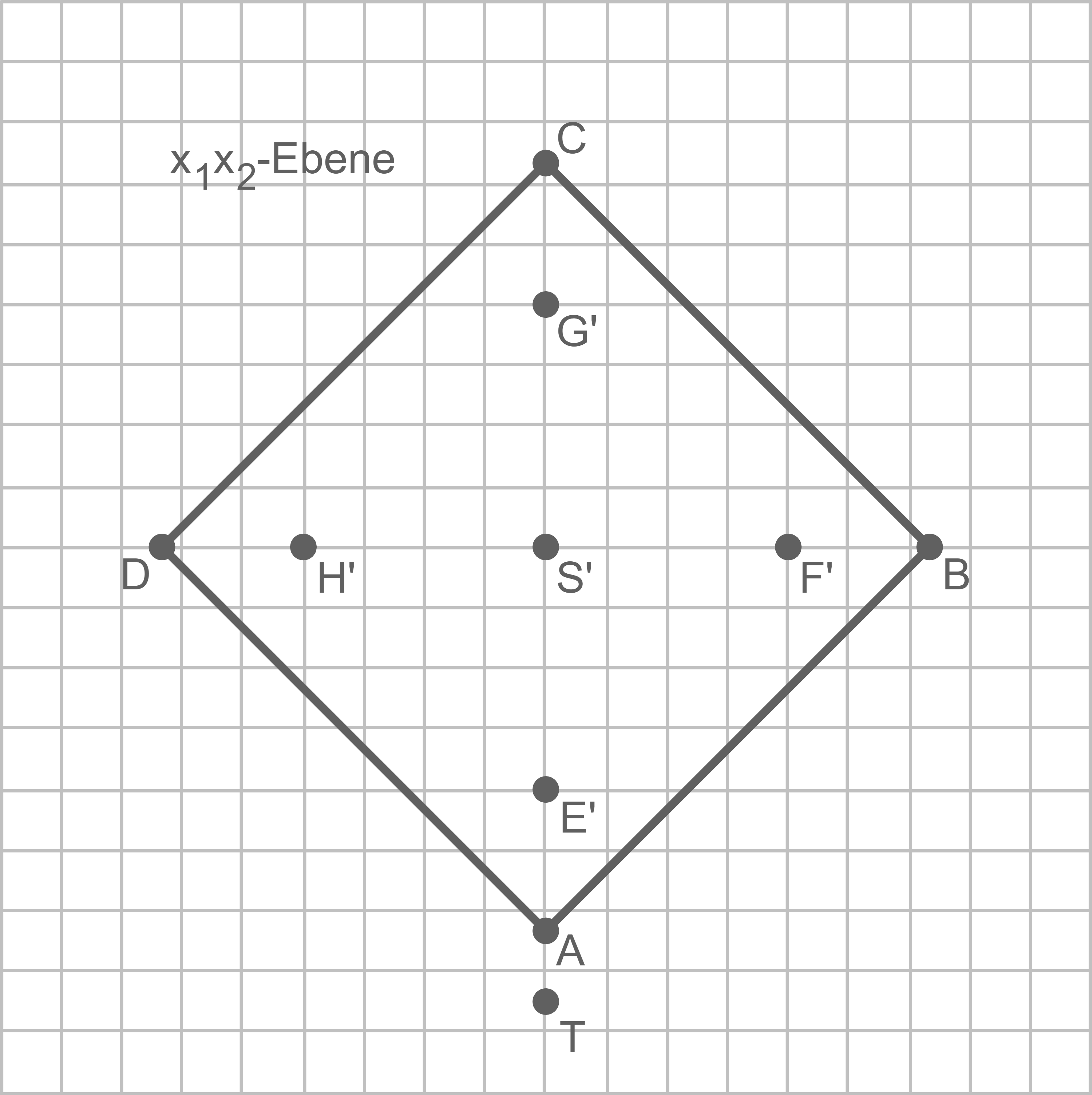
Zu einem bestimmten Zeitpunkt fallen auf die Knickpyramide Sonnenstrahlen, die im Modell durch parallele Geraden mit dem Richtungsvektor $\overrightarrow{S_{15} E}$ dargestellt werden. Der Schatten der Spitze der Knickpyramide auf dem horizontalen Boden wird durch den Punkt $T$ beschrieben. Die Lote durch die Punkte $E, F, G, H$ und $S_{15}$ auf die $x_1x_2$ -Ebene schneiden diese in den Punkten $\(E$ bzw. $\(S$ Diese sind zusammen mit der Grundfläche der Pyramide und dem Punkt $T$ in Abbildung 3 dargestellt.

Abb. 3

Berechne die Koordinaten von $T.$

(3 BE)

Der Schattenbereich der gesamten Pyramide auf dem Boden besteht im Modell aus zwei kongruenten Vierecken. Zeichne diesen Schattenbereich in Abbildung 3 ein und gib die besondere Form der genannten Vierecke an.

(4 BE)

(25 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Punkte $A$ und $B$ sowie $F$ und $E$ haben jeweils die gleichen $x_3$ -Koordinaten, somit sind die Seiten $\overline{AB}$ und $\overline{FE}$ des Vierecks parallel. Zudem gilt:

$\overline{EA}$ $= \left\vert\pmatrix{19\\0\\0} - \pmatrix{12\\0\\7}\right\vert$ $= \left\vert\pmatrix{7\\0\\-7}\right\vert$ $= \sqrt{7^2+0^2+(-7)^2}$ $= \sqrt{98}$

$\overline{BF}$ $= \left\vert\pmatrix{0\\12\\7} - \pmatrix{0\\19\\0}\right\vert$ $= \left\vert\pmatrix{0\\-7\\7}\right\vert$ $= \sqrt{0^2+(-7)^2+7^2}$ $= \sqrt{98}$

Somit ist das Viereck $ABFE$ ein Trapez mit zwei gleich langen Seiten.

Gleichung von $\boldsymbol{L}$ in Koordinatenform bestimmen

$\overrightarrow{AB}$ $= \pmatrix{0\\19\\0} - \pmatrix{19\\0\\0}$ $= \pmatrix{-19\\19\\0}$

$\overrightarrow{AE}$ $= \pmatrix{12\\0\\7} - \pmatrix{19\\0\\0}$ $= \pmatrix{-7\\0\\7}$

Ein Normalenvektor $\overrightarrow{n}$ der Ebene $L$ ergibt sich mit dem Vektorprodukt wie folgt:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \overrightarrow{AB}\times \overrightarrow{AE}\\[5pt] &=& \pmatrix{-19\\19\\0}\times\pmatrix{-7\\0\\7} \\[5pt] &=& \pmatrix{19\cdot 7 - 0\cdot 0 \\ 0\cdot (-7) -(-19)\cdot 7 \\ -19\cdot 0-19\cdot (-7)} \\[5pt] &=& \pmatrix{133\\133\\133}\\[5pt] &=& 133\cdot \pmatrix{1\\1\\1} \end{array}$

Es kann der gekürzte Vektor $\(\overrightarrow{n$ verwendet werden.

$L:1\cdot x_1+1\cdot x_2+1\cdot x_3=d$

Punktprobe mit $A$ liefert:

$\begin{array}[t]{rll} 1\cdot 19+1\cdot 0+1\cdot 0&=& d \\[5pt] 19&=& d \end{array}$

Eine Gleichung von $L$ in Koordinatenform ist somit gegeben durch:

$L:\,x_1+x_2+x_3-19=0$

Größe des Winkels $\boldsymbol{\varphi}$ bestimmen

Ein Normalenvektor der Ebene $L$ ist der eben bestimmte Vektor $\pmatrix{1\\1\\1}.$ Als Normalenvektor der $x_1x_2$ -Ebene kann $\pmatrix{0\\0\\1}$ gewählt werden, sodass für den eingeschlossenen Winkel folgt:

$\begin{array}[t]{rll} \cos(\varphi)&=&\dfrac{\pmatrix{1\\1\\1}\circ\pmatrix{0\\0\\1}}{\left|\pmatrix{1\\1\\1} \right|\cdot\left|\pmatrix{0\\0\\1} \right|} \\[5pt] &=&\dfrac{1\cdot 0 +1\cdot 0 +1\cdot 1}{\sqrt{1^2+1^2+1^2}\cdot\sqrt{1^2}} \\[5pt] &=&\dfrac{1}{\sqrt{3}} \end{array}$

Somit gilt $\varphi$ $= \cos^{-1}\left(\dfrac{1}{\sqrt{3}}\right)$ $\approx 54,74^\circ.$

Damit die Pyramide $EFGHS_k$ den Körper $ABCDEFGH$ zu einer großen Pyramide $ABCDS_k$ ergänzt, müssen z.B. die Punkte $A,$ $E$ und $S_k$ auf einer gemeinsamen Gerade liegen. Das ist der Fall, wenn die Vektoren $AE$ und $AS_k$ kollinear sein. Mit Hilfe von Aufgabenteil b) folgt:

$\overrightarrow{AE}$ $= \pmatrix{-7\\0\\7}$

$\overrightarrow{AS_k}$ $= \pmatrix{0\\0\\k}-\pmatrix{19\\0\\0}$ $= \pmatrix{-19\\0\\k}$

Weiter soll gelten:

$\pmatrix{-19\\0\\k}$ $= s\cdot\pmatrix{-7\\0\\7}$

Die erste Zeile liefert $s = \frac{19}{7},$ Einsetzen in die dritte Zeile liefert dann $k$ $= \frac{19}{7}\cdot 7$ $= 19.$

Pyramide $\boldsymbol{EFGHS_{15}}$ einzeichnen

Größe des Winkels begründen

Der Punkt $N$ ist der Mittelpunkt der Strecke $\overline{EF}.$ Die drei Punkte $M, N$ und $S_{15}$ bilden also ein rechtwinkiges Dreieck mit rechtem Winkel in $M,$ dessen Hypothenuse innerhalb der Seitenfläche $EFS_{15}$ verläuft.
Der Innenwinkel $\alpha$ dieses Dreiecks im Punkt $N$ entspricht dem betrachteten Winkel, den die Seitenfläche und die Grundfläche einschließen.
Da die Winkelsumme eines Dreiecks $180^\circ$ beträgt, sind die beiden Basiswinkel gleichgroß, wenn sie jeweils $45^\circ$ betragen. In diesem Fall handelt es sich um ein gleichschenkliges Dreieck, sodass damit auch die Strecken $\overline{MS_{15}}$ und $\overline{MN}$ gleichlang sind.
Wenn nun wie gegeben $\overline{MS_{15}}\lt\overline{MN}$ gilt, ist die Seitenfläche $EFS_{15}$ stärker nach innen geneigt, sodass der Winkel im Punkt $N$ sich verkleinert, das heißt die Größe des eingeschlossenen Winkels ist weniger als $45^\circ$ groß.

Höhenänderung bestimmen

Der höchste Punkt des Bauwerks ist die Spitze $S_{15}.$ Da diese gegenüber der geplanten Spitze $S_{19}$ genau $4\;\text{LE}$ tiefer liegt, ergibt sich eine Höhenänderung von $4\cdot7$ $= 28\;[\text{m}].$

Neigungswinkel begründen

Nach Aufgabenteil a) beträgt der Neigungswinkel im unteren Teil der Pyramide ca. $54,74^\circ,$ während er nach Aufgabenteil d) im oberen Teil kleiner als $45^\circ$ ist. Somit ist im unteren Teil des Bauwerks der Neigungswinkel der Seitenflächen gegenüber dem Boden um mindestens $54,74^\circ-45^\circ$ $= 9,74^\circ$ größer als im oberen Teil des Bauwerks, also um mehr als $9^\circ.$

1. Schritt: Geradengleichung aufstellen

$\overrightarrow{S_{15}E}$ $= \pmatrix{12\\0\\7}-\pmatrix{0\\0\\15}$ $= \pmatrix{12\\0\\-8}$

Die Sonnenstrahlen die durch die Spitze der Knickpyramide verlaufen, werden somit durch folgende Geradengleichung beschrieben:

$g:\overrightarrow{x}$ $= \overrightarrow{S_{15}} + t\cdot \overrightarrow{S_{15}E}$ $= \pmatrix{0\\0\\15} + t \cdot \pmatrix{12\\0\\-8}$

2. Schritt: Koordinaten von $\boldsymbol{T}$ berechnen

$T$ ist der Schnittpunkt der Geraden mit der $x_1x_2$ -Ebene und hat somit die $x_3$ -Koordinate $0.$ Somit folgt für $t:$

$\begin{array}[t]{rll} 15-8t&=& 0 &\quad \scriptsize \mid\;-15 \\[5pt] -8t&=& -15 &\quad \scriptsize \mid\;:(-8) \\[5pt] t&=&\dfrac{15}{8} \end{array}$

Einsetzen in die Geradengleichung liefert den Punkt $T:$

$\overrightarrow{OT} = \pmatrix{0\\0\\15} + \dfrac{15}{8} \cdot \pmatrix{12\\0\\-8}$ $= \pmatrix{22,5\\0\\0}$

Der Punkt $T$ besitzt somit die Koordinaten $T(22,5\mid 0\mid 0).$

Schattenbereich einzeichnen

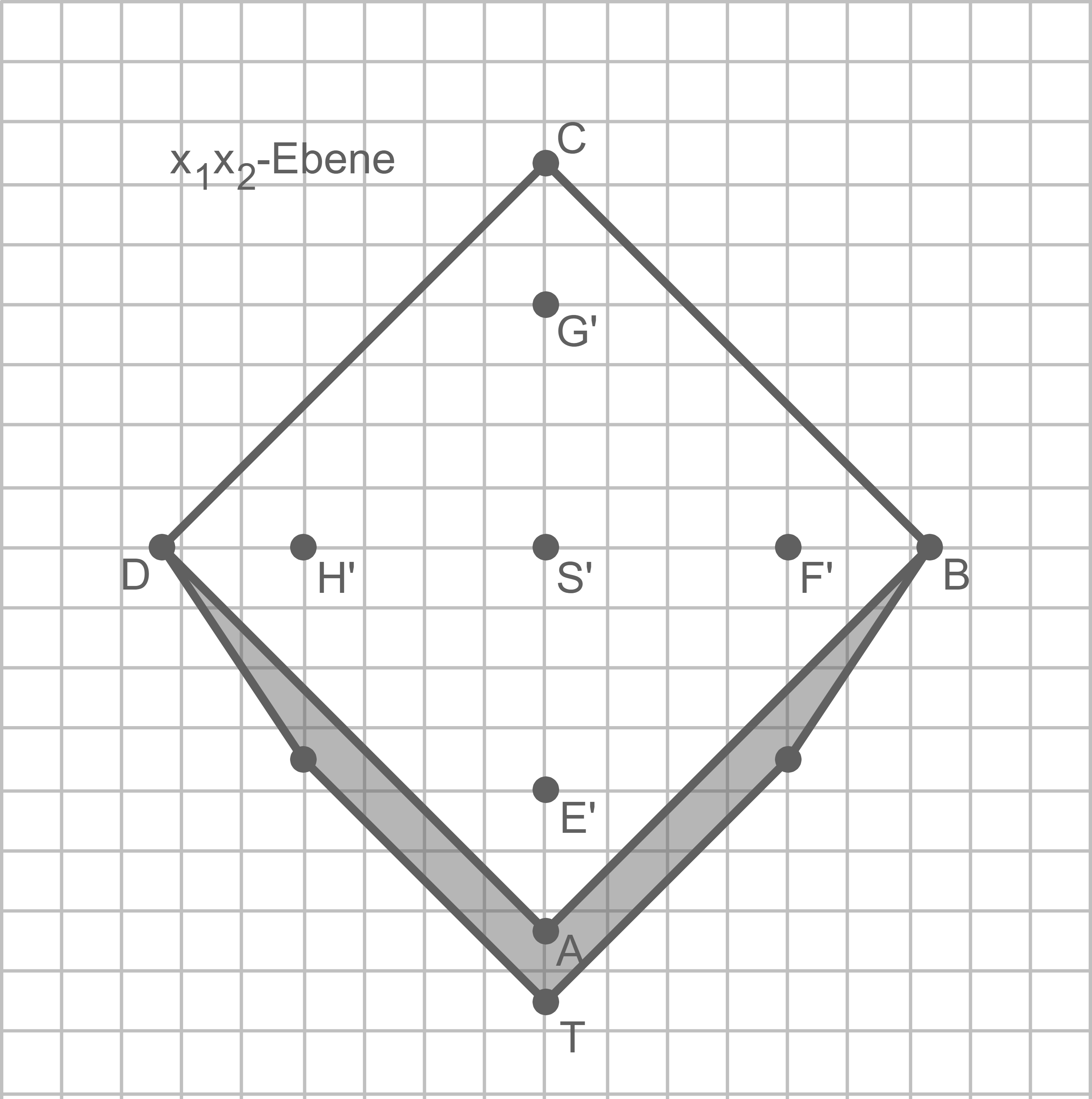Form der Vierecke angeben

Der Schattenbereich besteht aus zwei zueinander kongruenten Trapezen, die die Strecke $\overline{AT}$ gemeinsam haben.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?