Teil B
1
Die Abbildung zeigt den Graphen der in 
definierten Funktion 
Der Graph ist symmetrisch bezüglich seines Wendepunkts 
definierten Funktion Der Graph ist symmetrisch bezüglich seines Wendepunkts
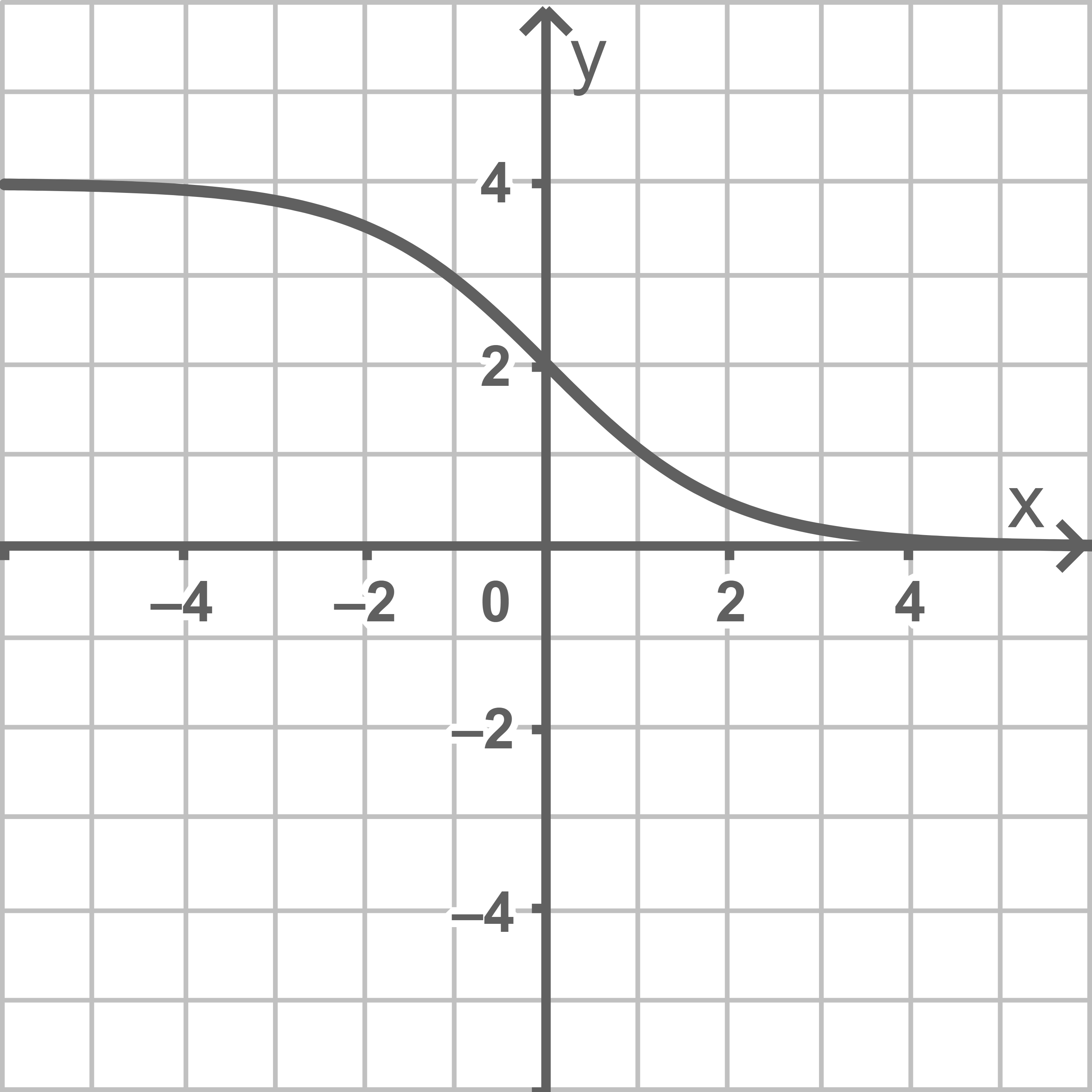
a)
Begründe anhand des Funktionsterms von 
dass 
keine Nullstelle hat, und gib 
sowie 
an.
dass keine Nullstelle hat, und gib sowie an.
(3 BE)
b)
Berechne die mittlere Steigung des Graphen von im Bereich 
auf Hundertstel genau und bestimme grafisch die Steigung des Graphen von in seinem Wendepunkt.
im Bereich auf Hundertstel genau und bestimme grafisch die Steigung des Graphen von in seinem Wendepunkt.
(5 BE)
c)
Für die in definierte erste Ableitungsfunktion 
von gilt 
Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von an und skizziere in der Abbildung den Graphen von 
Betrachtet wird die in definierte erste Ableitungsfunktion von gilt Gib die Bedeutung dieser Tatsache im Hinblick auf den Verlauf des Graphen von an und skizziere in der Abbildung den Graphen von
(3 BE)
definierte Funktion 
d)
Zeige, dass die Funktion 
eine Stammfunktion von ist.
eine Stammfunktion von ist.
(3 BE)
e)
Beurteile die folgende Aussage:
Der Graph von verläuft vollständig unterhalb der 
-Achse.
verläuft vollständig unterhalb der -Achse.
(3 BE)
f)
Begründe, dass der Wert des Integrals 
für jede positive reelle Zahl 
ohne Verwendung einer Stammfunktion von exakt bestimmt werden kann, und gib den Wert des Integrals an.
für jede positive reelle Zahl ohne Verwendung einer Stammfunktion von exakt bestimmt werden kann, und gib den Wert des Integrals an.
(4 BE)
2
Betrachtet wird die Schar der in definierten Funktionen 
mit 
und 
Die Funktion aus Aufgabe 1 ist eine Funktion dieser Schar.
beschrieben, die im Folgenden mit 
bezeichnet wird. Es gilt also 
Dabei ist die seit der Ansiedlung vergangene Zeit in Jahren und 
die Anzahl der Seeadler.
beschrieben werden. Das folgende Gleichungssystem ermöglicht die Bestimmung der zugehörigen Werte von 
und 
definierten Funktionen mit und Die Funktion aus Aufgabe 1 ist eine Funktion dieser Schar.
a)
Jeder der abgebildeten Graphen I, II und III der Schar gehört, bei festen Werten von 
und 
, zu einem der Werte von 
und 
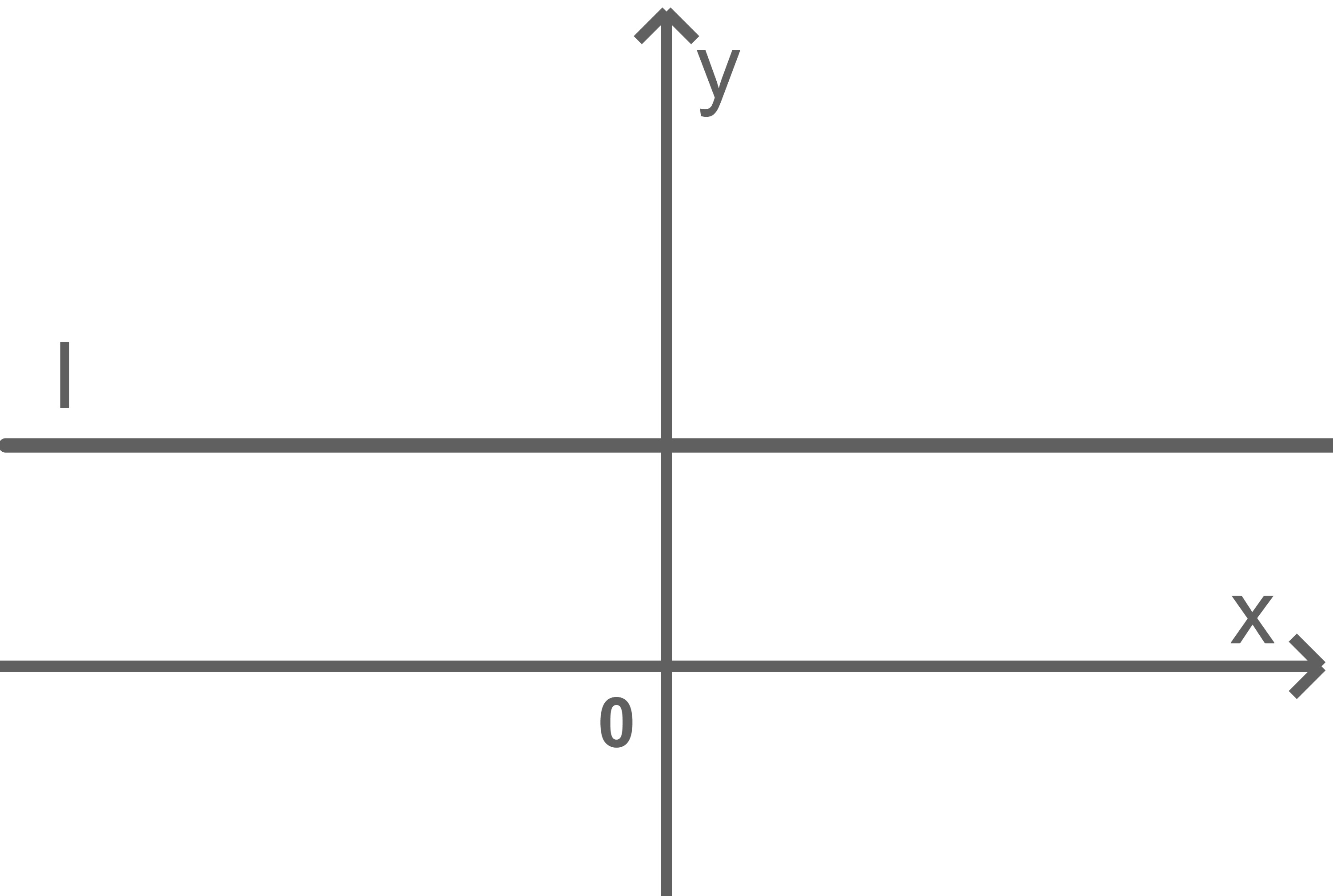
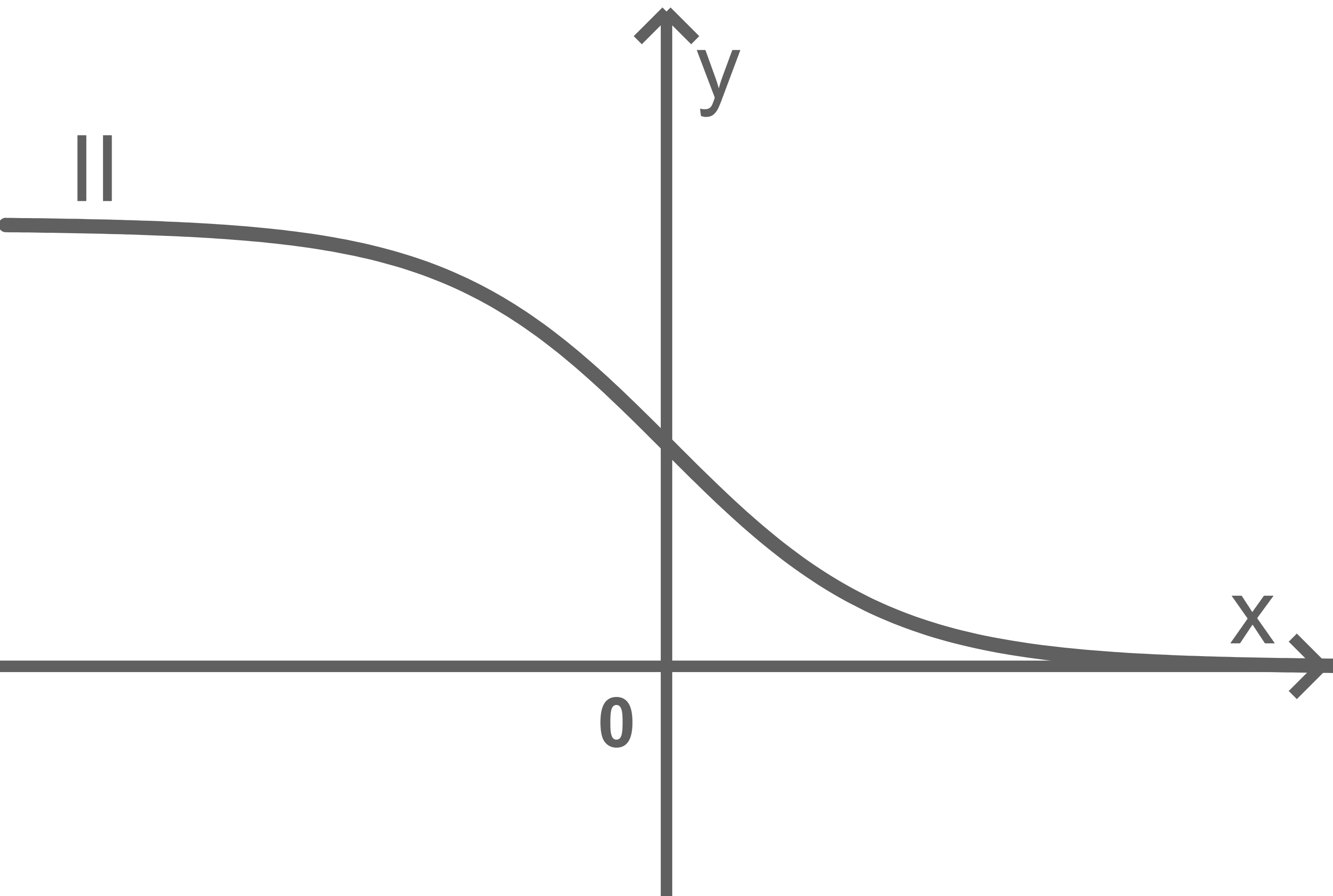
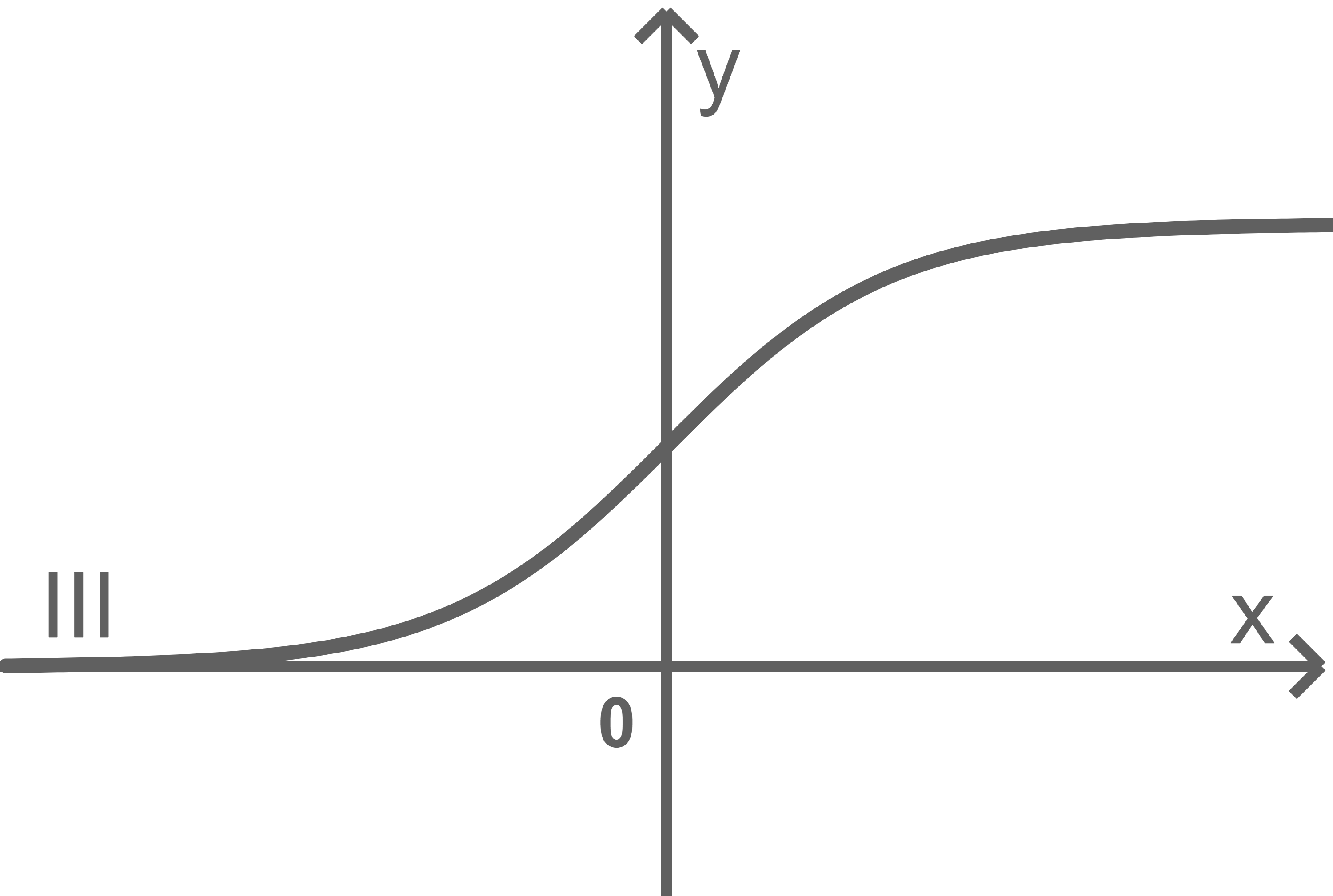Ordne den Graphen die genannten Werte von 
zu und begründe deine Zuordnung.
Auf einer Inselgruppe wurden Seeadler neu angesiedelt. Betrachtet wird die anschließende Entwicklung der Anzahl der Seeadler. In einem Modell wird diese Entwicklung mithilfe des Graphen der Funktion und , zu einem der Werte von und
zu und begründe deine Zuordnung.
(4 BE)
beschrieben, die im Folgenden mit bezeichnet wird. Es gilt also Dabei ist die seit der Ansiedlung vergangene Zeit in Jahren und die Anzahl der Seeadler.
b)
Gib auf Grundlage des Modells an, wie viele Seeadler angesiedelt wurden, und berechne, nach wie vielen Jahren die Anzahl der Seeadler auf 
angewachsen ist.
angewachsen ist.
(4 BE)
c)
Die Tangente an den Graphen von im Punkt 
hat die Steigung 
Würde die Entwicklung der Anzahl der Seeadler im Modell mithilfe dieser Tangente beschrieben werden, so ergäbe sich für den Zeitpunkt vier Jahre nach der Ansiedlung eine bestimmte Anzahl von Seeadlern. Untersuche, ob diese Anzahl mit denjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von ergeben würde.
Unter bestimmten anderen Gegebenheiten auf der Inselgruppe kann die Entwicklung der Anzahl der Seeadler im Modell mithilfe des Graphen einer anderen Funktion aus der Schar der Funktionen im Punkt hat die Steigung Würde die Entwicklung der Anzahl der Seeadler im Modell mithilfe dieser Tangente beschrieben werden, so ergäbe sich für den Zeitpunkt vier Jahre nach der Ansiedlung eine bestimmte Anzahl von Seeadlern. Untersuche, ob diese Anzahl mit denjenigen übereinstimmt, die sich bei einer Beschreibung mithilfe des Graphen von ergeben würde.
(3 BE)
beschrieben werden. Das folgende Gleichungssystem ermöglicht die Bestimmung der zugehörigen Werte von und
d)
Interpretiere jede der drei Gleichungen im Sachzusammenhang.
(3 BE)
e)
Ermittle die Werte von und 
und
(5 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Die Funktion 
hat keine Nullstellen, da der Zähler keine Nullstellen besitzt. Daher kann 
niemals 0 werden. Für die gesuchten Grenzwerte gilt:
hat keine Nullstellen, da der Zähler keine Nullstellen besitzt. Daher kann niemals 0 werden. Für die gesuchten Grenzwerte gilt:
b)
Die mittlere Steigung 
des Graphen von im Bereich wird durch den folgenden Differenzenquotienten berechnet:
Für die benötigten Funktionswerte folgt:
Somit ergibt sich:
![\(\begin{array}[t]{rll}
m&=&\dfrac{\frac{4}{1+\mathrm{e}} - \frac{4}{1+\frac{1}{\mathrm{e}}}}{2} \\[5pt]
&\approx&\dfrac{-1,848}{2} \\[5pt]
&=&-0,92
\end{array}\)](https://www.schullv.de/resources/formulas/ce99a26c25912a173c85b2fe235fd484b066b470235454733452ad1a316ee15f_light.svg)
Die graphische Bestimmung der Steigung des Graphen von im Wendepunkt 
mit Hilfe der Abbildung liefert eine Steigung von ungefähr 
des Graphen von im Bereich wird durch den folgenden Differenzenquotienten berechnet:
Für die benötigten Funktionswerte folgt:
Somit ergibt sich:
Die graphische Bestimmung der Steigung des Graphen von im Wendepunkt mit Hilfe der Abbildung liefert eine Steigung von ungefähr
c)
Bedeutung angeben
Die Gleichung 
bedeutet, dass der Graph der Ableitungsfunktion achsensymmetrisch zur 
-Achse verläuft.
Graphen skizzieren
bedeutet, dass der Graph der Ableitungsfunktion achsensymmetrisch zur -Achse verläuft.
Graphen skizzieren
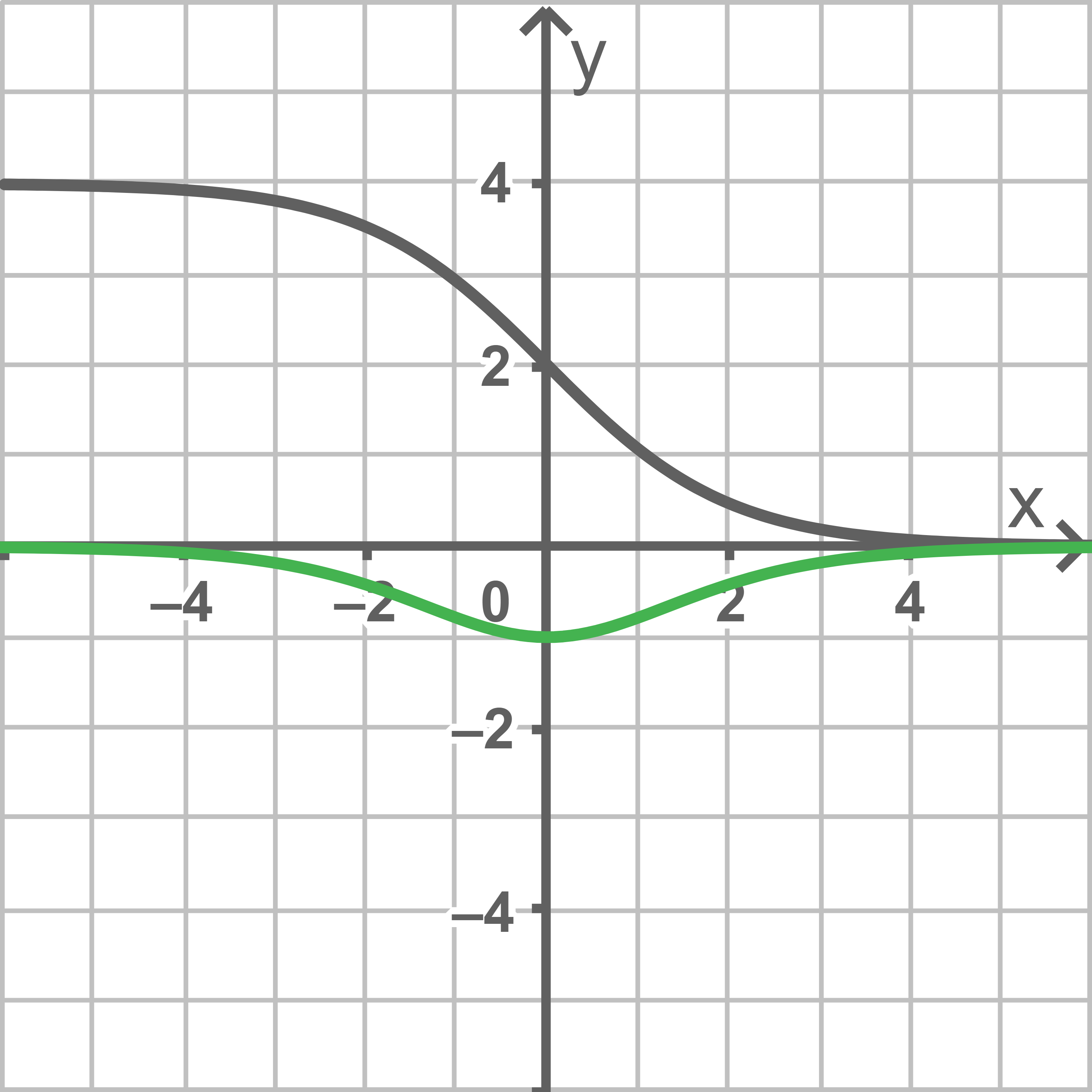
d)
Mit der Kettenregel folgt:
![\(\begin{array}[t]{rll}
F](https://www.schullv.de/resources/formulas/94df7f4b1d12c6c7566426d3b531f12b869079b9ac6d35378385078aaca1b04c_light.svg)
e)
Für 
gilt 
Für eine mögliche Nullstelle von muss gelten:
Somit besitzt keine Nullstelle, das heißt der Graph von verläuft vollständig unterhalb der -Achse. Die Aussage ist damit richtig.
gilt Für eine mögliche Nullstelle von muss gelten:
Somit besitzt 
![\(\begin{array}[t]{rll}
F(x)&=&0 \\[5pt]
4x-4\ln(\mathrm e^x+1)&=&0 &\quad \scriptsize \mid\;+4\ln(\mathrm e^x+1) \\[5pt]
4x&=&4\ln(\mathrm e^x+1) &\quad \scriptsize \mid\;:4 \\[5pt]
x&=&\ln(\mathrm e^x+1) \\[5pt]
\mathrm e^x&=&\mathrm e^x+1 &\quad \scriptsize \mid\;-\mathrm e^x \\[5pt]
0&=&1
\end{array}\)](https://www.schullv.de/resources/formulas/99e97beb951ad939f86436e63af304f00a8060b4945d1f531f5dbb153ceb0f6e_light.svg)
keine Nullstelle, das heißt der Graph von verläuft vollständig unterhalb der -Achse. Die Aussage ist damit richtig.
f)
Die Funktion ist symmetrisch bezüglich des Wendepunkts und besitzt als waagerechte Asymptoten 
und 
Damit liefert das Integral immer den gleichen Wert wie der Inhalt eines Rechtecks mit den Seitenlängen und 
Somit folgt:
ist symmetrisch bezüglich des Wendepunkts und besitzt als waagerechte Asymptoten und Damit liefert das Integral immer den gleichen Wert wie der Inhalt eines Rechtecks mit den Seitenlängen und Somit folgt:
2
a)
- Graph I gehört zu
da der Graph eine konstante Funktion darstellt. - Graph II gehört zu
da die dargestellte Funktion streng monoton fallend ist und hier somit 
gelten muss. - Graph III gehört zu
da die dargestellte Funktion hier streng monoton steigend ist und somit 
gilt.
b)
Angesiedelte Seeadler angeben
Anzahl der Jahre berechnen
Es dauert somit ungefähr 
Jahre, bis die Seeadlerpopulation auf anwächst.
Anzahl der Jahre berechnen
Es dauert somit ungefähr 
![\(\begin{array}[t]{rll}
w(x)&=&32 \\[5pt]
\dfrac{40}{1+\mathrm{e}^{-0,2 x}}&=&32 &\quad \scriptsize \mid\;\cdot(1+\mathrm e^{-0,2x}) \\[5pt]
40&=&32\cdot(1+\mathrm e^{-0,2x}) &\quad \scriptsize \mid\;:32 \\[5pt]
\dfrac{40}{32}&=&1+\mathrm e^{-0,2x} &\quad \scriptsize \mid\;-1 \\[5pt]
\dfrac{8}{32}&=&\mathrm e^{-0,2x} \\[5pt]
\ln\left(\dfrac{8}{32}\right)&=&-0,2x &\quad \scriptsize \mid\;:(-0,2)\\[5pt]
6,93&\approx&x
\end{array}\)](https://www.schullv.de/resources/formulas/cd8ebd606958f695bbccfe1e94393ac3add743f03e8b1b3704e08f76595ab8a0_light.svg)
Jahre, bis die Seeadlerpopulation auf anwächst.
c)
Die Tangente an den Graphen von im Punkt hat die Steigung Wenn die Entwicklung der Anzahl der Seeadler mit dieser Tangente beschrieben werden würde, wäre die Anzahl der Seeadler nach vier Jahren 
Nach dem Graphen von ist die Anzahl der Seeadler nach vier Jahren gegeben durch:
Da die Anzahl der Seeadler ganzzahlig sein muss, wird auf 
gerundet. Die Anzahl der Seeadler bei der Beschreibung mit der Tangente stimmt somit mit der Anzahl der Seeadler bei der Beschreibung mit Hilfe des Graphen von überein.
im Punkt hat die Steigung Wenn die Entwicklung der Anzahl der Seeadler mit dieser Tangente beschrieben werden würde, wäre die Anzahl der Seeadler nach vier Jahren Nach dem Graphen von ist die Anzahl der Seeadler nach vier Jahren gegeben durch:
Da die Anzahl der Seeadler ganzzahlig sein muss, wird auf gerundet. Die Anzahl der Seeadler bei der Beschreibung mit der Tangente stimmt somit mit der Anzahl der Seeadler bei der Beschreibung mit Hilfe des Graphen von überein.
d)
- Gleichung
gibt den Wert 
an. Die Gleichung besagt somit, dass 
Seeadler neu angesiedelt werden. - Gleichung
beschreibt, wie viele Seeadler es auf lange Sicht geben wird. Diese Anzahl beträgt 
- Gleichung
gibt die Anzahl der Seeadler 15 Jahre nach der Neuansiedlung an, welche 
beträgt.
e)
Aus Gleichung folgt:
![\(\begin{array}[t]{rll}
\dfrac{a}{b+1}&=&20 &\quad \scriptsize \mid\;\cdot(b+1) \\[5pt]
a&=&20b+20
\end{array}\)](https://www.schullv.de/resources/formulas/e0d60d4b863250b815be93743643d1e266e3289c0535804bcee1cd77e068b045_light.svg)
Einsetzen in liefert:
Für positive Werte von gilt 
und der Bruch würde gegen 
gehen. Da der Grenzwert des Bruches allerdings 
ergibt, muss entweder negativ sein oder 
gelten. Für stimmen die linke Seite der Gleichungen und überein. Da jedoch 
gilt, muss somit negativ sein und es gilt 
Damit liefert Gleichung weiter:
![\(\begin{array}[t]{rll}
\dfrac{20b+20}{b}&=&45 &\quad \scriptsize \mid\;\cdot b \\[5pt]
20b+20&=&45b &\quad \scriptsize \mid\;-20b \\[5pt]
20&=&25b &\quad \scriptsize \mid\;:25 \\[5pt]
\dfrac{4}{5}&=&b
\end{array}\)](https://www.schullv.de/resources/formulas/3dae62fc78085ec1530320ffd9088ff9e2cd9b0cdabde552d5858746f3dfaba8_light.svg)
Einsetzen in 
liefert für 
Somit ergeben sich die Werte 
und 
folgt:
Einsetzen in liefert:
Für positive Werte von gilt und der Bruch würde gegen gehen. Da der Grenzwert des Bruches allerdings ergibt, muss entweder negativ sein oder gelten. Für stimmen die linke Seite der Gleichungen und überein. Da jedoch gilt, muss somit negativ sein und es gilt Damit liefert Gleichung weiter:
Einsetzen in liefert für
Somit ergeben sich die Werte und