Teil B
1
Gegeben ist die in  definierte Funktion
definierte Funktion 
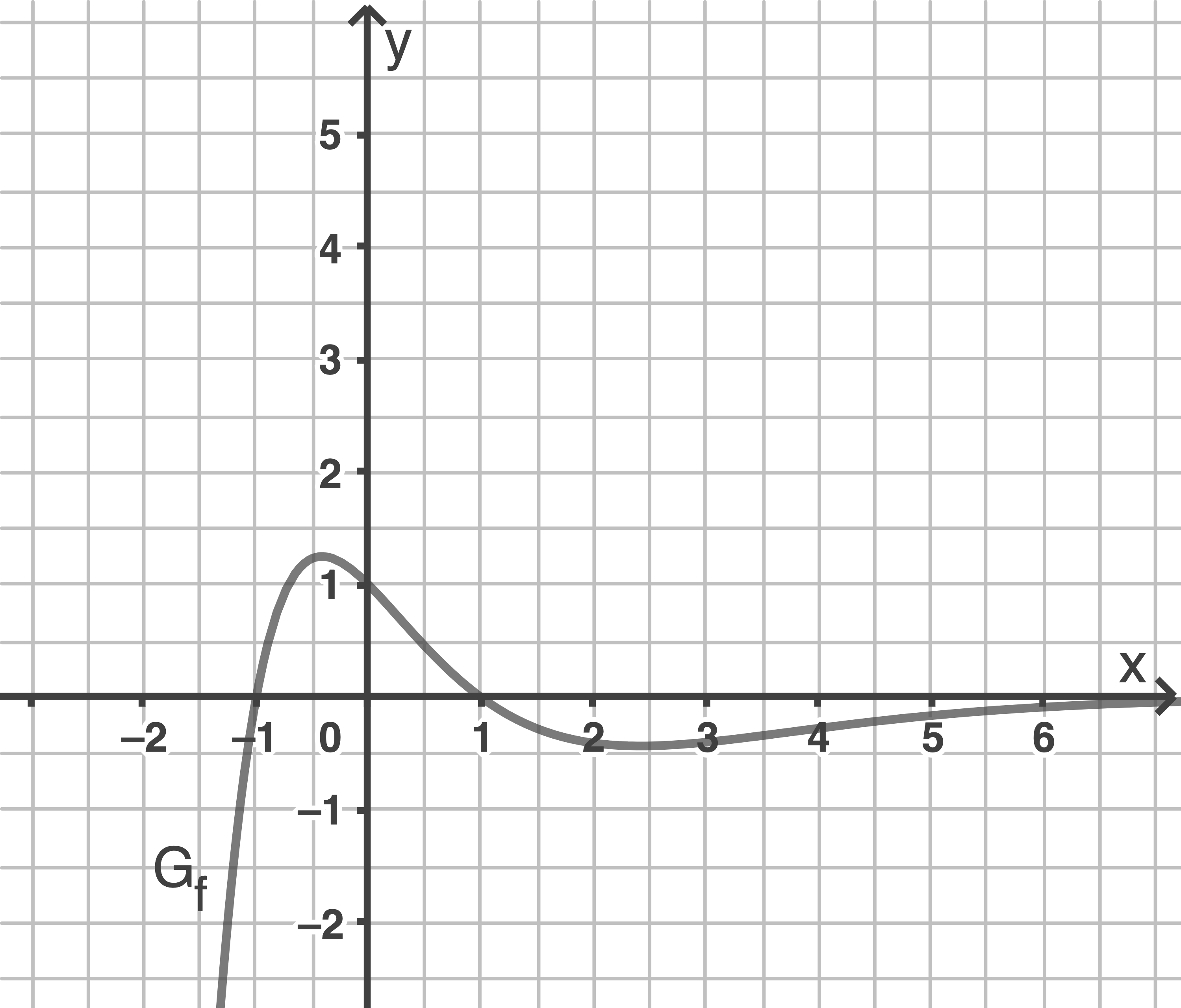
Die Abbildung zeigt den Graphen von
von 
 definierte Funktion
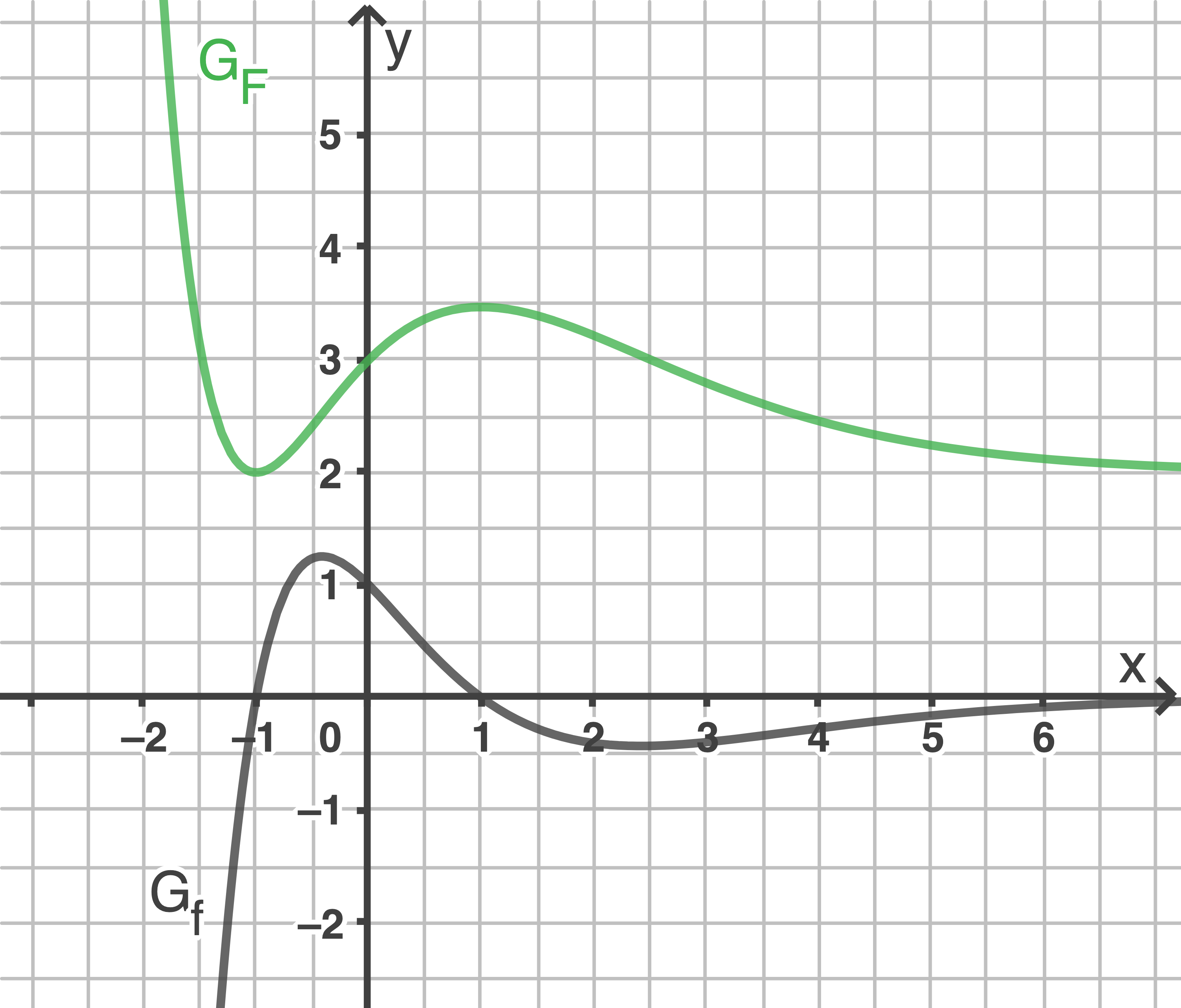
definierte Funktion  ist diejenige Stammfunktion von
ist diejenige Stammfunktion von  deren Graph durch den Punkt
deren Graph durch den Punkt  verläuft.
verläuft.
 definierten Funktionen
definierten Funktionen  mit
mit  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet.
bezeichnet.
Für ergibt sich die bisher betrachtete Funktion
ergibt sich die bisher betrachtete Funktion 
Die Abbildung zeigt den Graphen

a)
Zeige, dass  genau zwei Nullstellen besitzt.
genau zwei Nullstellen besitzt.
(2 BE)
b)
Bestimme rechnerisch die  -Koordinaten der beiden Extrempunkte von
-Koordinaten der beiden Extrempunkte von  [Zur Kontrolle:
[Zur Kontrolle:  ]
]
(4 BE)
c)
Ermittle anhand der Abbildung einen Näherungswert für das Integral 
Die in
d)
Begründe mithilfe der Abbildung, dass der Graph von  im Punkt
im Punkt  einen Tiefpunkt besitzt.
einen Tiefpunkt besitzt.
(2 BE)
e)
Skizziere in der Abbildung den Graphen von  . Berücksichtige dabei insbesondere, dass
. Berücksichtige dabei insbesondere, dass  und
und  gilt.
gilt.
(3 BE)
f)
Deute die Aussage  in Bezug auf
in Bezug auf  geometrisch.
geometrisch.
Betrachtet wird nun die Schar der in
(2 BE)
Für
g)
Gib in Abhängigkeit von  die Anzahl der Nullstellen von
die Anzahl der Nullstellen von  an.
an.
(2 BE)
h)
Für einen bestimmten Wert von  besitzt
besitzt  zwei Schnittpunkte mit der
zwei Schnittpunkte mit der  -Achse, die voneinander den Abstand 4 haben. Berechne diesen Wert.
-Achse, die voneinander den Abstand 4 haben. Berechne diesen Wert.
(3 BE)
i)
Beurteile, ob es einen Wert von  gibt, sodass
gibt, sodass  und
und  bezüglich der
bezüglich der  -Achse symmetrisch zueinander liegen.
-Achse symmetrisch zueinander liegen.
(2 BE)
2
Betrachtet wird die in  definierte Funktion
definierte Funktion  Ihr Graph wird mit
Ihr Graph wird mit  bezeichnet.
bezeichnet.
a)
Zeige, dass  streng monoton zunehmend ist und die Wertemenge
streng monoton zunehmend ist und die Wertemenge ![\(]0;1[\)](https://mathjax.schullv.de/abcbe6aa6f94b3cb46c96e2187212549f6dc3ceba7745679326455ec65bcd4f6?color=5a5a5a) besitzt.
besitzt.
 Zur Kontrolle:
Zur Kontrolle: 
![\(\bigg]\)](https://mathjax.schullv.de/4b61dd2dabbb8b74e78b937540addb1f8bc242927b45ff99fcc77bdb1a7dc91d?color=5a5a5a)
(5 BE)
b)
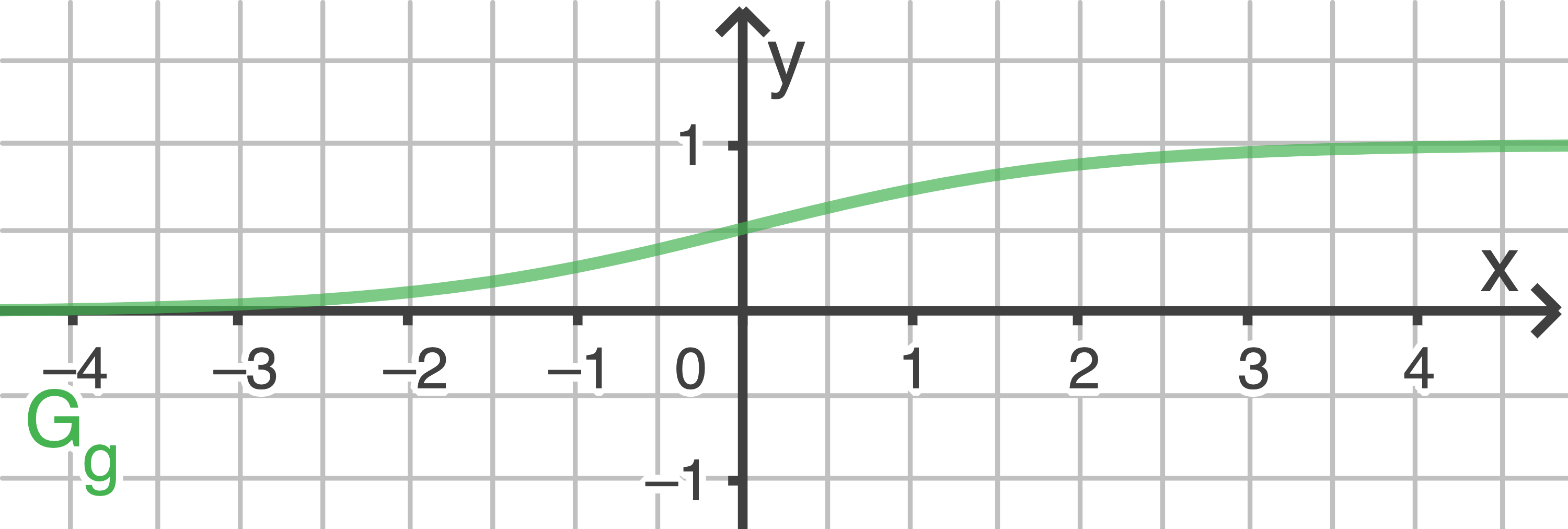
Gib  an und zeichne
an und zeichne  im Bereich
im Bereich  unter Berücksichtigung der bisherigen Ergebnisse und der Tatsache, dass
unter Berücksichtigung der bisherigen Ergebnisse und der Tatsache, dass  in
in  seinen einzigen Wendepunkt hat, in ein Koordinatensystem ein.
seinen einzigen Wendepunkt hat, in ein Koordinatensystem ein.
(3 BE)
c)
Der Graph der Funktion  geht aus
geht aus  durch Strecken und Verschieben hervor. Die Wertemenge von
durch Strecken und Verschieben hervor. Die Wertemenge von  ist
ist ![\(]-1;1[.\)](https://mathjax.schullv.de/ddfb8486ae50bf9daba37c099ebf6249099822c7a51a963b74ffd50746b9107d?color=5a5a5a) Gib einen möglichen Funktionsterm für
Gib einen möglichen Funktionsterm für  an.
an.
(2 BE)
d)
Es wird das Flächenstück zwischen  und der
und der  -Achse im Bereich
-Achse im Bereich  mit
mit  betrachtet. Bestimme den Wert von
betrachtet. Bestimme den Wert von  so, dass die
so, dass die  -Achse dieses Flächenstück halbiert.
-Achse dieses Flächenstück halbiert.
(6 BE)
(40) BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Für Nullstellen von  gilt
gilt 

Da für alle
für alle  ist, folgt mit dem Satz vom Nullprodukt, dass
ist, folgt mit dem Satz vom Nullprodukt, dass  genau dann gilt, wenn
genau dann gilt, wenn  gilt. Diese quadratische Gleichung hat genau zwei Lösungen,
gilt. Diese quadratische Gleichung hat genau zwei Lösungen,  sodass
sodass  genau zwei Nullstellen besitzt.
genau zwei Nullstellen besitzt.
Da
b)
Mit der Produktregel ergibt sich für die erste Ableitung von  Anwendung der notwendigen Bedingung für Extremstellen liefert:
Anwendung der notwendigen Bedingung für Extremstellen liefert:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/f73df321bf636adb9180b954910e97d278bef634926b88b9c0de51ee3857720d?color=5a5a5a) Mit der
Mit der  -Formel folgt:
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1;2} &=& \dfrac{2\pm \sqrt{(-2)^2 +4}}{2}\\[5pt]
&=& \dfrac{2\pm \sqrt{8}}{2} \\[5pt]
x_1&\approx& 2,41 \\[5pt]
x_2&\approx& -0,41
\end{array}\)](https://mathjax.schullv.de/d9fce22170bb8dd878e89d12ff7f7f3b05a7d3063e20e62c5f8703872bed17af?color=5a5a5a) Da die Aufgabenstellung besagt, dass es genau zwei Extrempunkte gibt, muss die hinreichende Bedingung nicht überprüft werden. Die
Da die Aufgabenstellung besagt, dass es genau zwei Extrempunkte gibt, muss die hinreichende Bedingung nicht überprüft werden. Die  -Koordinaten der beiden Extrempunkte von
-Koordinaten der beiden Extrempunkte von  lauten somit
lauten somit  und
und 
c)
Im Intervall ![\([-1; 1]\)](https://mathjax.schullv.de/0e40990ce56fd6e58e73f1d6bcd18453ef929b7e875d4908e6368bd020413ea0?color=5a5a5a) schließt
schließt  oberhalb der
oberhalb der  -Achse mit dieser ca. 6 Kästchen ein, im Intervall
-Achse mit dieser ca. 6 Kästchen ein, im Intervall ![\([1; 4]\)](https://mathjax.schullv.de/c4d160189eb54f717436d112883adaa09f77d2e19aabc417d6b48043d7a858d8?color=5a5a5a) ca. 4 Kästchen unterhalb der
ca. 4 Kästchen unterhalb der  -Achse. Da ein Kästchen ca.
-Achse. Da ein Kästchen ca. ![\(0,5\cdot 0,5 = 0,25\;[\text{FE}]\)](https://mathjax.schullv.de/fc01080d354a266ad511794fa89beeecaecbdc0aac2571368547a922f0e874cd?color=5a5a5a) entspricht, folgt:
entspricht, folgt:
![\(\begin{array}[t]{rll}
\displaystyle\int_{-1}^{4}f(x)\;\mathrm dx&\approx&6\cdot 0,25 - 4\cdot 0,25 \\[5pt]
&=&0,5\;[\text{FE}]
\end{array}\)](https://mathjax.schullv.de/570efb987a946c7ccdfc32255fbae755c70f140ddb9c28d1c26f65a20c1c6fad?color=5a5a5a)
d)
Der Graph von  hat an der Stelle
hat an der Stelle  eine Nullstelle mit Vorzeichenwechsel von Minus zu Plus. Mit dem Vorzeichenwechselkriterium folgt somit, dass der Graph von
eine Nullstelle mit Vorzeichenwechsel von Minus zu Plus. Mit dem Vorzeichenwechselkriterium folgt somit, dass der Graph von  an dieser Stelle einen Tiefpunkt besitzt.
an dieser Stelle einen Tiefpunkt besitzt.
e)
f)
Im Intervall ![\([0; 2,5]\)](https://mathjax.schullv.de/7634f281f09100b68377ca28c3f96ddcae567aeadc1caeb48694c9c2a44622a2?color=5a5a5a) ist die Fläche, die
ist die Fläche, die  mit der
mit der  -Achse oberhalb dieser einschließt, genauso groß wie die Fläche, die
-Achse oberhalb dieser einschließt, genauso groß wie die Fläche, die  mit der
mit der  -Achse unterhalb dieser einschließt.
-Achse unterhalb dieser einschließt.
g)
Da stets  gilt, ergeben sich die Nullstellen von
gilt, ergeben sich die Nullstellen von  mit dem Satz vom Nullprodukt als die des Terms
mit dem Satz vom Nullprodukt als die des Terms  Da
Da  und
und  immer größer als Null sind, folgt:
immer größer als Null sind, folgt:
- Für
besitzt
keine Nullstelle
- Für
besitzt
zwei Nullstellen
h)
Für die Nullstellen von  mit
mit  gilt:
gilt:
![\(\begin{array}[t]{rll}
h_k(x) &=& 0 \\[5pt]
(1-kx^2)\cdot \mathrm{e}^{-x} &=& 0 &\quad \scriptsize \mid\;:\mathrm{e}^{-x} \\[5pt]
1-k x^2 &=& 0 &\quad \scriptsize \mid\; -1 \\[5pt]
-kx^2&=&-1 &\quad \scriptsize \mid\;:(-k) \\[5pt]
x^2 &=& \dfrac{1}{k} \\[5pt]
x &=& \pm\sqrt{\dfrac{1}{k}}
\end{array}\)](https://mathjax.schullv.de/c0d5466a655660e7861028cc77023a61455c2eb3c53cf0d9e07e2210fc945b0b?color=5a5a5a) Da die beiden Schnittpunkte mit der
Da die beiden Schnittpunkte mit der  -Achse, das heißt die beiden Nullstellen, den Abstand 4 voneinander haben sollen, folgt:
-Achse, das heißt die beiden Nullstellen, den Abstand 4 voneinander haben sollen, folgt:
![\(\begin{array}[t]{rll}
\sqrt{\dfrac{1}{k}}- \left(-\sqrt{\dfrac{1}{k}} \right) &=& 4 \\[5pt]
2 \sqrt{\dfrac{1}{k}} &=& 4&\quad \scriptsize \mid\; :2 \\[5pt]
\sqrt{\dfrac{1}{k}} &=& 2 &\quad \scriptsize \mid\;^2 \\[5pt]
\dfrac{1}{k} &=& 4 &\quad \scriptsize \mid\;\cdot k\\[5pt]
1 &=& 4k &\quad \scriptsize \mid\;:4\\[5pt]
\dfrac{1}{4} &=& k
\end{array}\)](https://mathjax.schullv.de/4221b9784f492b279648e6545b42b102918e0c586b2881fd0fb99089362c1cba?color=5a5a5a) Für
Für  haben die beiden Schnittpunkte von
haben die beiden Schnittpunkte von  mit der
mit der  -Achse somit den Abstand 4 voneinander.
-Achse somit den Abstand 4 voneinander.
i)
Damit die beiden Graphen  und
und  bezüglich der
bezüglich der  -Achse symmetrisch zueinander liegen, müssen
-Achse symmetrisch zueinander liegen, müssen  und
und  mindestens die gleichen Nullstellen besitzen. Die Nullstellen von
mindestens die gleichen Nullstellen besitzen. Die Nullstellen von  folgen aus Aufgabenteil a) als
folgen aus Aufgabenteil a) als  und
und  Gleichsetzen von
Gleichsetzen von  mit der positiven Nullstelle von
mit der positiven Nullstelle von  aus Aufgabenteil h) liefert:
aus Aufgabenteil h) liefert:
![\(\begin{array}[t]{rll}
1 &=& \sqrt{\dfrac{1}{k}} &\quad \scriptsize \mid\;^2 \\[5pt]
1 &=& \dfrac{1}{k} &\quad \scriptsize \mid\; \cdot k\\[5pt]
k&=& 1
\end{array}\)](https://mathjax.schullv.de/19d733148d51ae0adb12cdfc7e45c0d7dbb3a81394e9debbb551dff64f303e1e?color=5a5a5a) Da
Da  gilt, gibt es somit keinen weiteren Graphen
gilt, gibt es somit keinen weiteren Graphen  der die gleichen Nullstellen wie
der die gleichen Nullstellen wie  besitzt, und damit keinen Graphen
besitzt, und damit keinen Graphen  der bezüglich der
der bezüglich der  -Achse symmetrisch zu
-Achse symmetrisch zu  liegt.
liegt.
2
a)
Streng monotone Zunahme zeigen
Mit der Quotientenregel folgt:
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/5267b4cbde7230bef36baf3ff9df53b2b90926d0bcdf5a90803b69578bb48943?color=5a5a5a) Da stets
Da stets  gilt, sind sowohl Zähler als auch Nenner stets positiv und es folgt
gilt, sind sowohl Zähler als auch Nenner stets positiv und es folgt  für alle
für alle  Somit ist
Somit ist  streng monoton zunehmend.
Wertemenge zeigen
Es gilt stets
streng monoton zunehmend.
Wertemenge zeigen
Es gilt stets  das heißt
das heißt  kann den Wert Null nicht annehmen. Zudem gilt
kann den Wert Null nicht annehmen. Zudem gilt  das heißt es folgt
das heißt es folgt  Weiterhin folgt:
Weiterhin folgt:
 die Wertemenge
die Wertemenge ![\(W=\;]0;1[.\)](https://mathjax.schullv.de/7414e6f8d076d6aa1e262f314247b49ac1abee40c3250545812451302a0bb641?color=5a5a5a)
b)
c)
Bei Verschiebung und Streckung eines Graphen in  -Richtung ändert sich auch die Wertemenge. Eine Verschiebung von
-Richtung ändert sich auch die Wertemenge. Eine Verschiebung von  um
um  Längeneinheiten in negative
Längeneinheiten in negative  -Richtung liefert somit das Intervall
-Richtung liefert somit das Intervall ![\(]-0,5;0,5[\)](https://mathjax.schullv.de/4f7ccea70a4cd03bb6b917bb1d1725c7d68c882c3a2869d8cf275f42a2918e8d?color=5a5a5a) als Wertemenge. Anschließende Streckung in
als Wertemenge. Anschließende Streckung in  -Richtung um den Faktor
-Richtung um den Faktor  liefert dann die Wertemenge
liefert dann die Wertemenge ![\(W^*=\;]-1;1[\)](https://mathjax.schullv.de/6a74025ef6e0601116db9ac2c79fa9e94959ef12bc644da44d2eefbfd018dee2?color=5a5a5a) von
von  Ein möglicher Funktionsterm von
Ein möglicher Funktionsterm von  lautet somit:
lautet somit:

d)