Teil B

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f: x \mapsto \frac{x^2-1}{x^2+1};$ die Abbildung 1 zeigt ihren Graphen $G_f.$

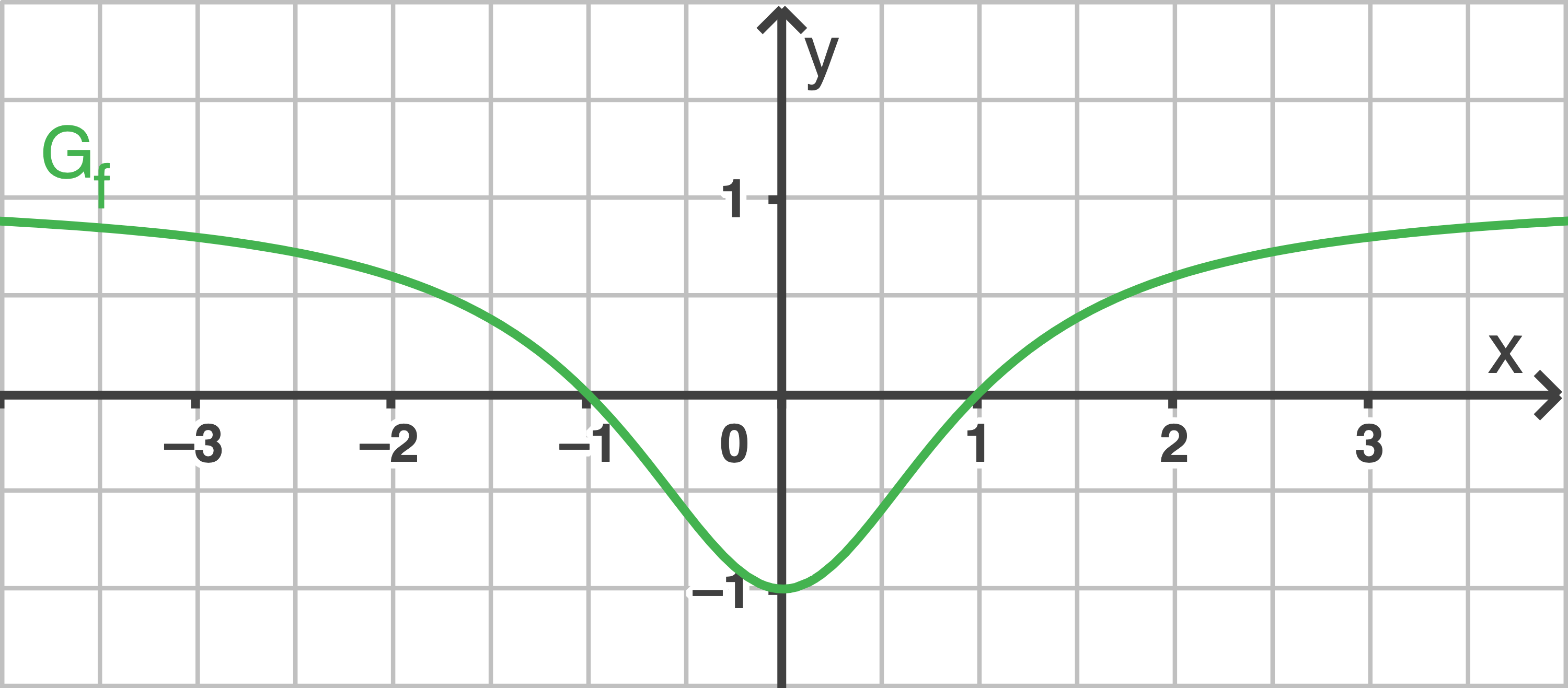
Graph einer Funktion mit grünem Verlauf auf Koordinatensystem. Achsen sind beschriftet.

Abb.1

Bestätige rechnerisch, dass $G_f$ symmetrisch bezüglich der $y$ -Achse ist, und untersuche anhand des Funktionsterms das Verhalten von $f$ für $x\rightarrow +{\infty}$ . Bestimme diejenigen $x$ -Werte, für die $f(x)=0,96$ gilt.

(5 BE)

Untersuche rechnerisch das Monotonieverhalten von $G_f.$

(zur Kontrolle: $\(f$ )

(4 BE)

Bestimme rechnerisch eine Gleichung der Tangente $t$ an $G_f$ im Punkt $(3\mid f(3))$ . Berechne die Größe des Winkels, unter dem $t$ die $x$ -Achse schneidet, und zeichne $t$ in die Abbildung 1 ein.

(4 BE)

Nun wird die in $\mathbb{R}$ definierte Integralfunktion $F: x \mapsto \displaystyle\int_{0}^{x}f(t)\;\mathrm dt$ betrachtet; ihr Graph wird mit $G_F$ bezeichnet.

Begründe, dass $F$ in $x=0$ eine Nullstelle hat und mache mithilfe des Verlaufs von $G_f$ plausibel, dass im Intervall $[1;3]$ eine weitere Nullstelle von $F$ liegt.
Gib an, welche besondere Eigenschaft $G_F$ im Punkt $(-1\mid F(-1))$ hat, und begründe deine Angabe.

(5 BE)

Die Gerade mit der Gleichung $y=x-1$ begrenzt gemeinsam mit den Koordinatenachsen ein Dreieck. Gib den Flächeninhalt dieses Dreiecks und den sich daraus ergebenden Näherungswert für $F(1)$ an.

(2 BE)

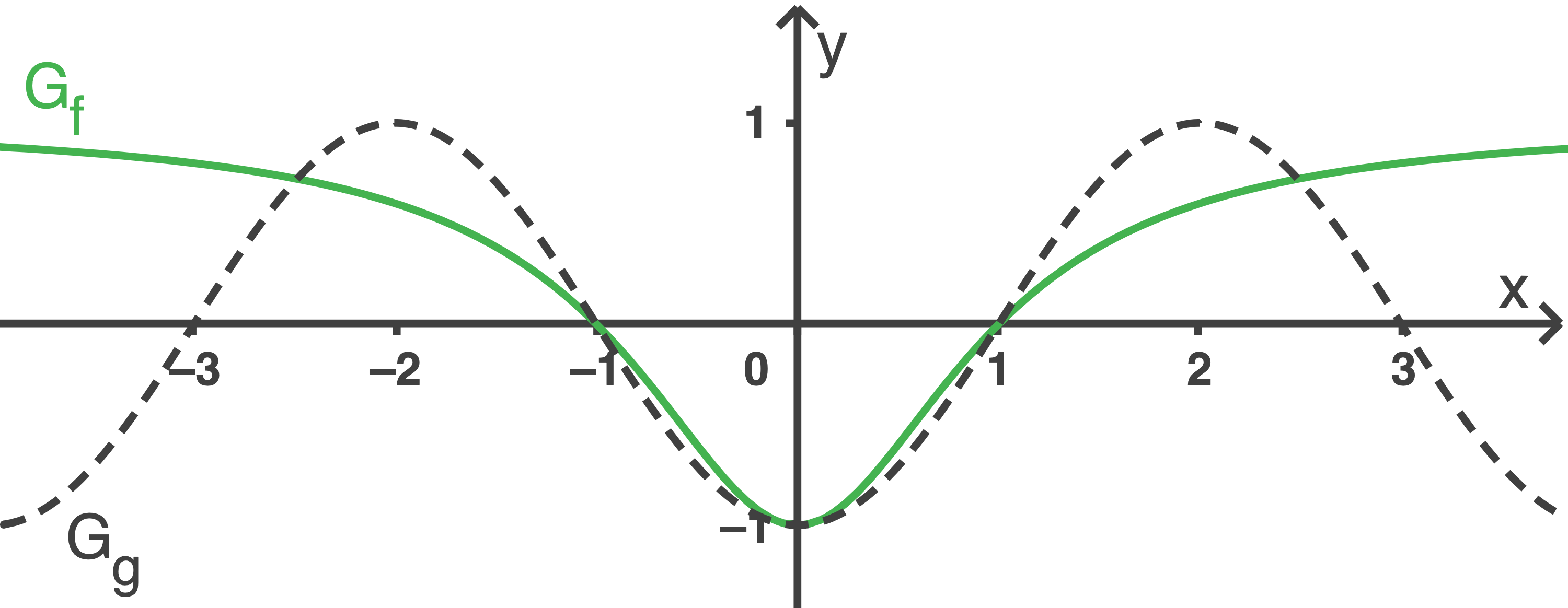
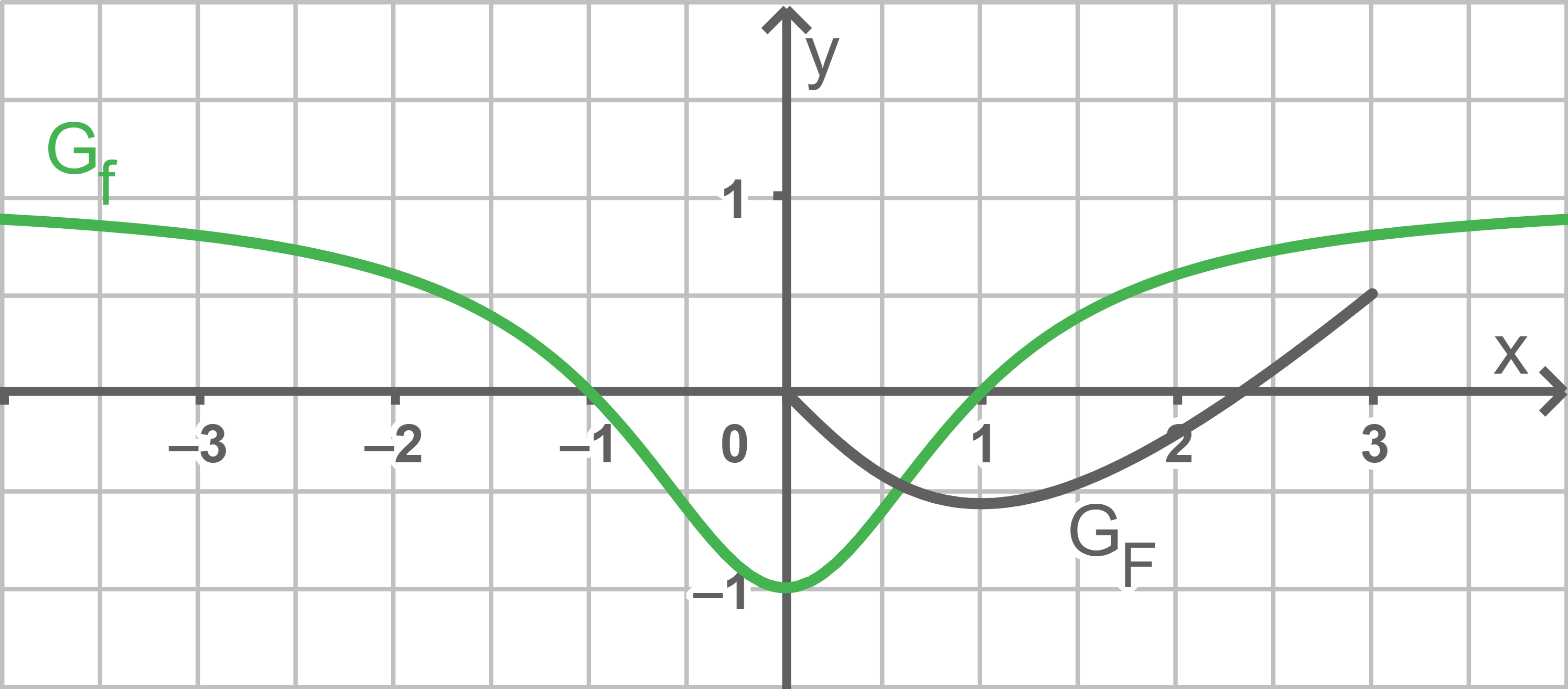
Die Abbildung 2 zeigt den Graphen $G_f$ sowie den Graphen $G_g$ der in $\mathbb{R}$ definierten Funktion $g : x \mapsto -\cos\left(\dfrac{\pi}{2}x \right).$
Beschreibe, wie $G_g$ aus dem Graphen der in $\mathbb{R}$ definierten Funktion $x \mapsto \cos \,x$ hervorgeht und berechne durch Integration von $g$ einen weiteren Näherungswert für $F(1).$

(zur Kontrolle: $F(1) \approx - \frac{2}{\pi }$ )

Graphische Darstellung von zwei Funktionen im Koordinatensystem mit Achsen und Bezeichnungen.

Abb. 2

(5 BE)

Berechne das arithmetische Mittel der beiden in den Aufgaben 2b und 2c berechneten Näherungswerte.
Skizziere den Graph von $F$ für $0 \leq x \leq 3$ unter Berücksichtigung der bisherigen Ergebnisse in der Abbildung 1.

(5 BE)

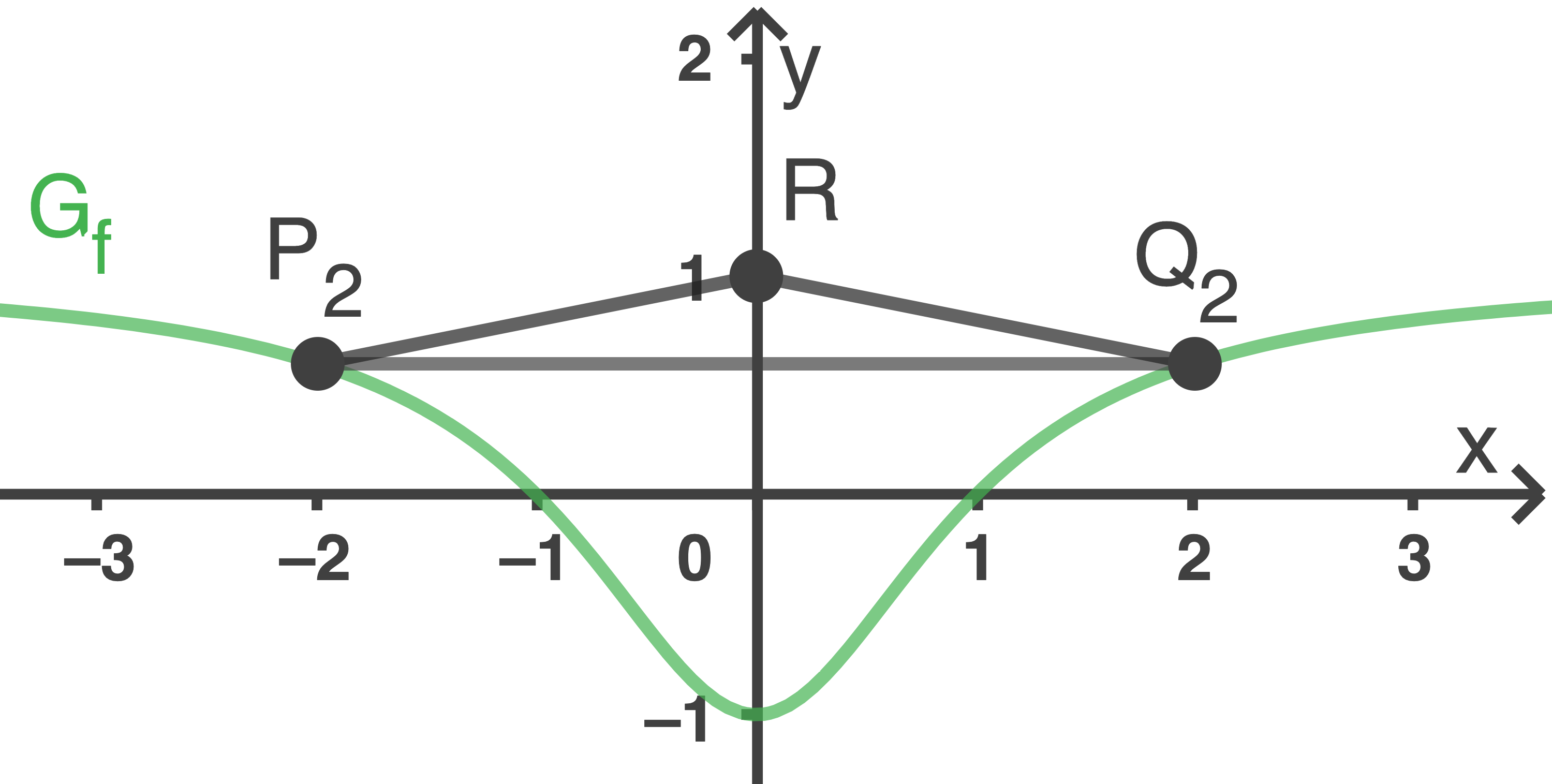
Für jeden Wert $k\gt 0$ legen die auf $G_f$ liegenden Punkte $P_k(-k\mid f(-k))$ und $Q_k(k\mid f(k))$ gemeinsam mit dem Punkt $R_k(0\mid 1)$ ein gleichschenkliges Dreieck $P_kQ_kR$ fest.

Berechne für $k=2$ den Flächeninhalt des zugehörigen Dreiecks $P_2Q_2R$ (vgl. Abbildung 3).
Zeige anschließend, dass der Flächeninhalt des Dreiecks $P_kQ_kR$ allgemein durch den Term $A(k)=\frac{2k}{k^2+1}$ beschrieben werden kann.

Graf einer Funktion mit Achsenbeschriftungen und Punkten P2 und Q2.

Abb. 3

(5 BE)

Zeige, dass es einen Wert von $k\gt 0$ gibt, für den $A(k)$ maximal ist. Berechne diesen Wert von $k$ sowie den Flächeninhalt des zugehörigen Dreiecks $P_kQ_kR.$

(6 BE)

(40 BE)

Da $f(-x)= \frac{(-x)^2-1}{(-x)^2+1}$ $= \frac{x^2-1}{x^2+1} = f(x)$ gilt, ist $G_f$ symmetrisch bezüglich der $y$ -Achse.
Da der Zähler und der Nenner des Funktionsterms von $f$ den gleichen Grad besitzen und die beiden Vorfaktoren dividiert durcheinander $1$ ergeben, gilt $\lim\limits_{x\to+\infty}f(x)=1.$

$\begin{array}[t]{rll} f(x)&=& 0,96 \\[5pt] \dfrac{x^2-1}{x^2+1} &=& 0,96&\quad \scriptsize \mid\;\cdot (x^2+1) \\[5pt] x^2-1&=& 0,96x^2+0,96&\quad \scriptsize \mid\;+1 \\[5pt] x^2&=& 0,96x^2+1,96&\quad \scriptsize \mid\;-0,96x^2 \\[5pt] 0,04x^2 &=&1,96 &\quad \scriptsize \mid\; :0,04 \\[5pt] x^2 &=&49 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt] x&=& \pm\sqrt{49} \end{array}$

Die $x$ -Werte, für die $f(x)=0,96$ gilt, lauten $x_1=7$ und $x_2=-7.$

Mit der Quotientenregel folgt für die erste Ableitung von $f:$

Rechenweg anzeigen

$\( f$

Der Nenner des Funktionsterms von $\(f$ ist stets positiv. Somit gilt insgesamt $\(f$ für $x\lt 0$ und $\(f$ für $x\gt 0.$
Der Graph $G_f$ ist damit streng monoton fallend für negative $x$ und streng monoton steigend für positive $x.$

Gleichung der Tangente $\boldsymbol{t}$ und Schnittwinkel berechnen

$f(3)= \dfrac{3^2-1}{3^2+1}= 0,8$

Für die Steigung $m$ der Tangente folgt:

$\(m= f$

Einsetzen von $m$ und den Koordinaten $(3\mid0,8)$ in den Funktionsterm $t(x)=mx+b$ liefert für $b:$

$\begin{array}[t]{rll} 0,8&=& 0,12 \cdot 3 +b \\[5pt] 0,8&=& 0,36 +b&\quad \scriptsize \mid\; -0,36 \\[5pt] 0,44&=&b \end{array}$

Die gesuchte Tangente $t$ ist somit gegeben durch $t:x\mapsto 0,12 x+0,44.$

Für den Schnittwinkel $\alpha$ von $t$ mit der $x$ -Achse folgt:

$\begin{array}[t]{rll} \tan(\alpha)&=&0,12 \\[5pt] \alpha&=&\tan^{-1}(0,12) \\[5pt] \alpha&\approx&6,83^\circ \end{array}$

Tangente einzeichnen

Die Integralfunktion $F(x)$ beschreibt die Flächenbilanz der vom Graphen der Funktion $f$ und der $x$ -Achse im Intervall zwischen $0$ und $x$ eingeschlossenen Fläche. Für $x=0$ wird keine Fläche eingeschlossen, somit gilt $F(0)=0.$

Im Intervall $[0;1]$ schließt $G_f$ mit der $x$ -Achse eine Fläche von ca. 2 Kästchen ein, welche unterhalb dieser liegt. Da $G_f$ im Intervall $[1;3]$ über der $x$ -Achse verläuft und mehr als 3 Kästchen mit dieser einschließt, existiert ein $x\in[1;3],$ sodass die im Intervall $[1;x]$ eingeschlossene Fläche genau so groß ist wie die zunächst betrachtete Fläche unterhalb der $x$ -Achse. Somit liegt im Intervall $[1;3]$ eine weitere Nullstelle von $F.$

Die Integralfunktion $F$ ist eine Stammfunktion von $f.$ Da $f$ bei $x=-1$ eine Nullstelle mit einem Vorzeichenwechsel von positiv zu negativ besitzt, hat $G_F$ im Punkt $(-1\mid F(-1))$ einen Hochpunkt.

Aus der Geradenform der Geraden mit der Gleichung $y=x-1$ ergeben sich der $y$ -Achsenabschnitt $b=-1$ und die Nullstelle $x=1.$ Für den Flächeninhalt $A$ des eingeschlossenen Dreiecks folgt somit:

$A= \dfrac{1}{2} \cdot 1 \cdot 1 = 0,5\;[\text{FE}]$

Aus der Abbildung 1 wird deutlich, dass die Gerade $y=x-1$ im Intervall $[0;1]$ eine gute Näherung des Graphen $G_f$ ist. Da die in diesem Intervall von $G_f$ mit der $x$ -Achse eingeschlossene Fläche unterhalb dieser liegt, folgt $F(1) \approx -0,5.$

$G_g$ geht aus dem Graphen des Kosinus durch Streckung in $x$ -Richtung mit dem Faktor $\frac{\pi}{2}$ und anschließende Spiegelung an der $x$ -Achse hervor. Ein weiterer Näherungswert von $F(1)$ ergibt sich somit wie folgt:

Rechenweg anzeigen

$F(1)\approx-\dfrac{2}{\pi}$

Arithmetisches Mittel berechnen

$\overline{F(1)}= \dfrac{-0,5 -\frac{2}{\pi}}{2} \approx -0,57$

Graph von $\boldsymbol{F}$ skizzieren

Da der Graph von $f$ nach Aufgabenteil 1a symmetrisch zur $y$ -Achse liegt, gilt $f(-2)=f(2)=\frac{2^2-1}{2^2+1}$ $=\frac{3}{5}=0,6$ und die Koordinaten der betrachteten Punkte ergeben sich zu $P_2(-2 \mid 0,6),$ $Q_2(2 \mid 0,6)$ und $R(0 \mid 1).$
Die Grundseite $a$ des gleichschenkligen Dreiecks beträgt somit $a=2-(-2)=4\;[\text{LE}]$ und die Höhe $h_a$ ergibt sich zu $h_a=1-0,6=0,4\;[\text{LE}].$ Für den Flächeninhalt $A_2$ des Dreiecks $P_2Q_2R$ folgt somit:

$A_2=\dfrac{1}{2} \cdot 0,4 \cdot 4 =0,8\;[\text{FE}]$

Für beliebiges $k$ gilt ebenfalls $f(k)=f(-k).$ Somit folgt für die Grundseite $a$ und die Höhe $h_a$ des Dreiecks $P_kQ_kR:$

$a= k-(-k)=2k$

$\begin{array}[t]{rll} h_a&=&1-f(k) \\[5pt] &=&1- \dfrac{k^2-1}{k^2+1} \\[5pt] &=&\dfrac{k^2+1-(k^2-1)}{k^2+1} \\[5pt] &=&\dfrac{2}{k^2+1} \end{array}$

Für den allgemeinen Flächeninhalt $A(k)$ folgt somit:

$A(k)= \dfrac{1}{2} \cdot2k \cdot \dfrac{2}{k^2+1}= \dfrac{2k }{k^2+1}$