Teil A
1
Gegeben ist die in 
definierte Funktion 
mit der Ableitungsfunktion 
a)
Berechne 
(2 BE)
b)
Bestimme einen Term derjenigen Stammfunktion 
von 
deren Graph durch den Punkt 
verläuft.
(3 BE)
2
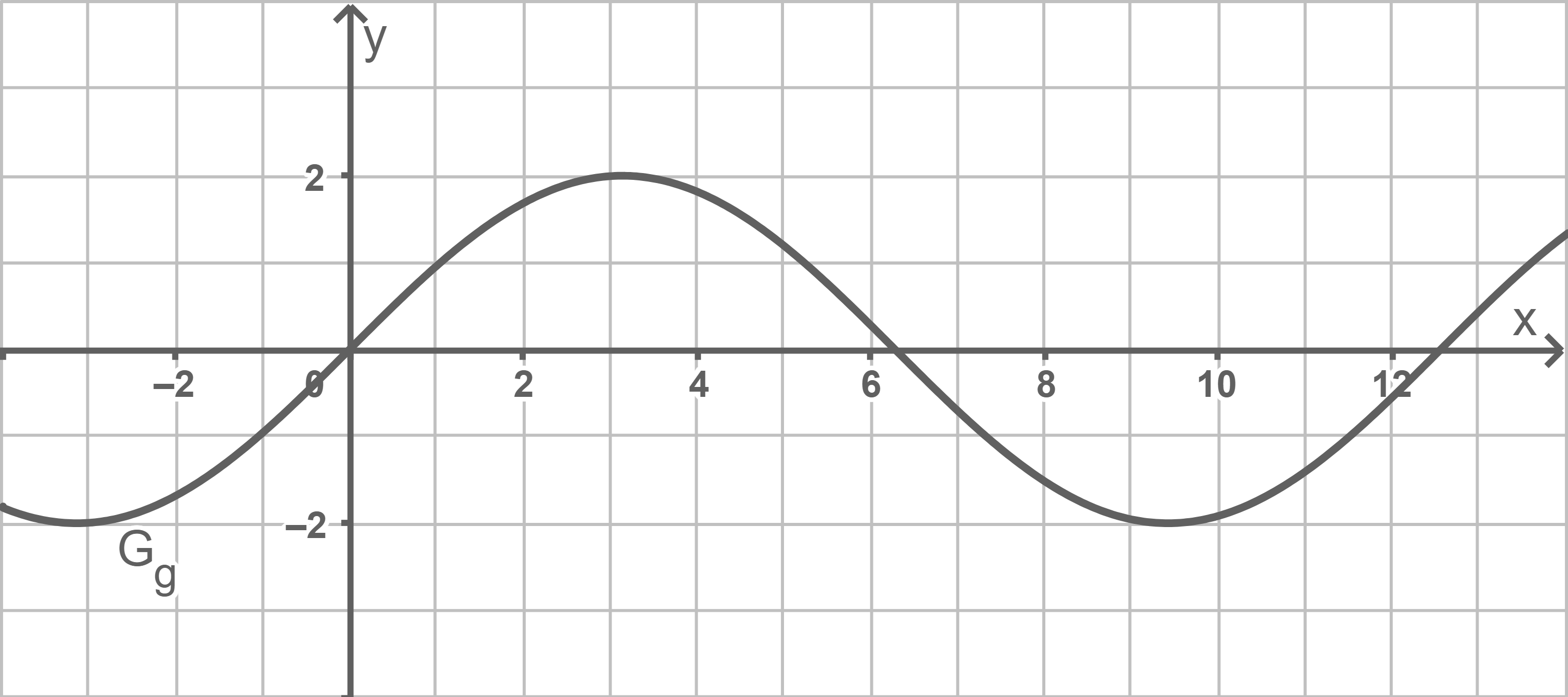
Die Abbildung zeigt den Graphen 
der in definierten Funktion 
mit 
a)
Beurteile mit Hilfe der Abbildung, ob der Wert des Integrals 
negativ ist.
(2 BE)
b)
Weise rechnerisch nach, dass die folgende Aussage zutrifft:
Die Tangente an im Koordinatenursprung ist die Gerade durch die Punkte 
und 
(3 BE)
3
Betrachtet wird die Schar der in definierten Funktionen 
mit 
und 
Für jeden Wert von 
besitzt die Funktion genau eine Extremstelle.
a)
Begründe, dass der Graph von für 
unterhalb der 
-Achse verläuft.
(2 BE)
b)
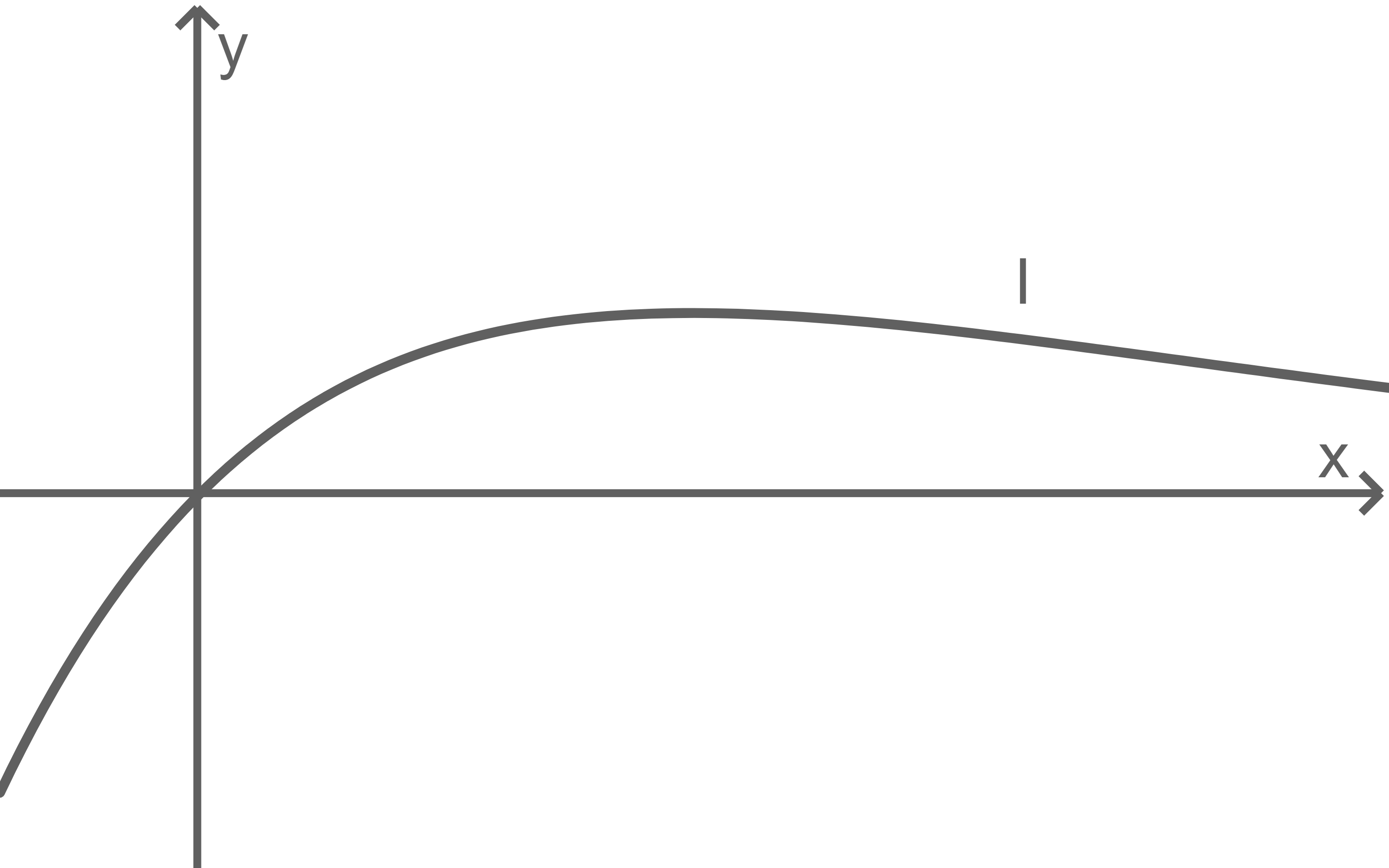
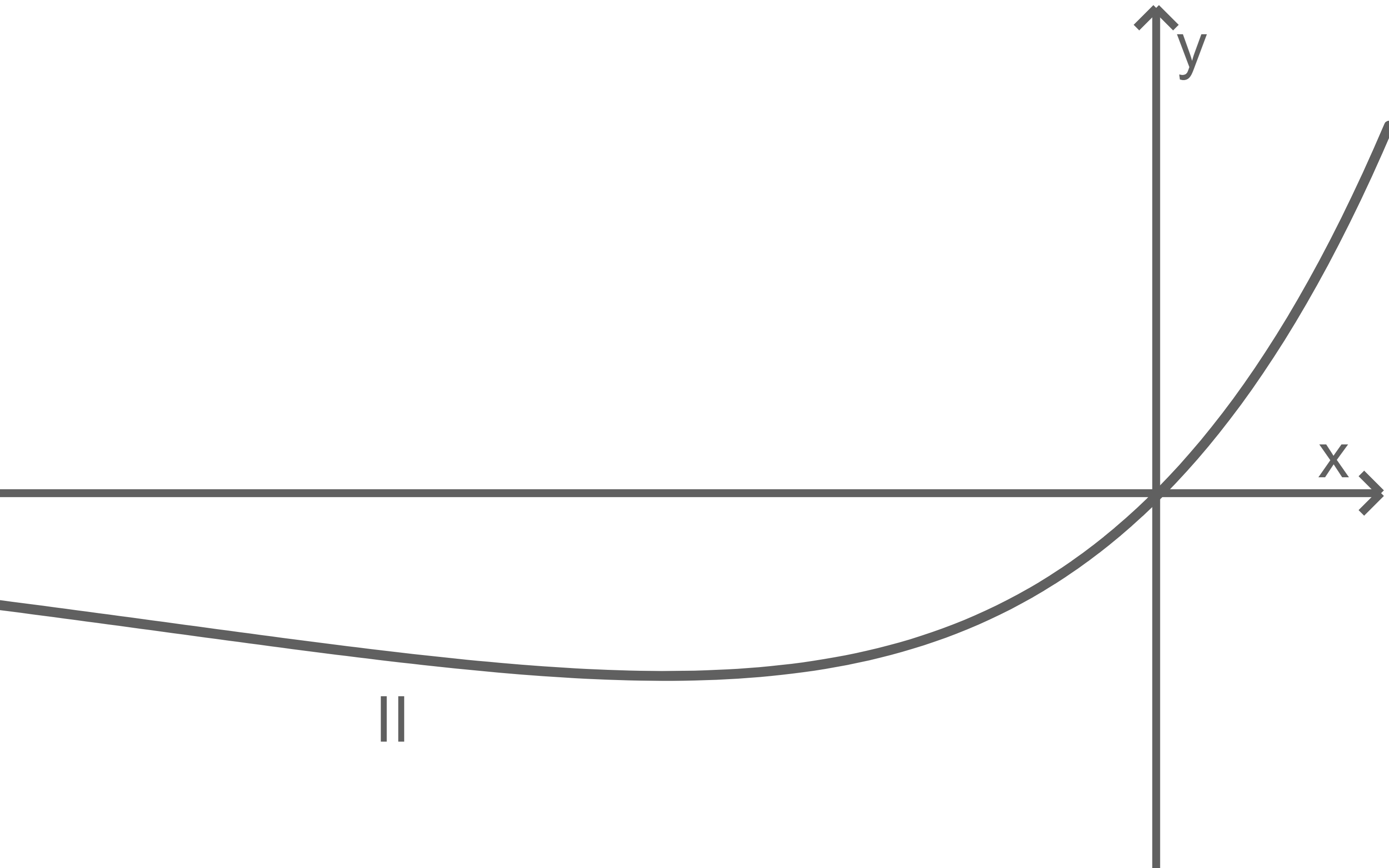
Die abgebildeten Graphen I und II sind Graphen der Schar; einer der beiden gehört zu einem positiven Wert von 
Entscheide, welcher Graph dies ist, und begründe deine Entscheidung.
(3 BE)
4
a)
Gib einen Term einer in definierten Funktion an, die den Wertebereich ![\([-2 ; 4]\)](https://mathjax.schullv.de/61f4d6607acbc82a40acade8b2aced3e2a066043b31522333792022441fe1cbf?color=5a5a5a)
hat.
(2 BE)
b)
Gib einen Term einer in definierten Funktion 
an, sodass der Term 
genau für ![\(x \in[-2 ; 4]\)](https://mathjax.schullv.de/da22e6dff581b96042298314521cfaa0d5d7d24d01b3602e107961acc6555231?color=5a5a5a)
definiert ist. Erläutere die deiner Angabe zugrunde liegenden Überlegungen.
(3 BE)
(20 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
Alle Stammfunktionen der Funktion 
haben die folgende Form:
![\(\begin{array}[t]{rll}
F(x)&=&\displaystyle\int f(x)\;\mathrm dx \\[5pt]
&=&\displaystyle\int 8x^3+3x\;\mathrm dx \\[5pt]
&=&\dfrac{1}{4}\cdot8x^4+\dfrac{1}{2}\cdot3x^2+c \\[5pt]
&=&2x^4+\dfrac{3}{2}x^2+c
\end{array}\)](https://mathjax.schullv.de/a8611d47189c69580222f71464eaa41af67c25de256f9f3eb0d716fe39c95d60?color=5a5a5a)
Einsetzen der Koordinaten 
liefert:
![\(\begin{array}[t]{rll}
F(-1)&=&5 \\[5pt]
2\cdot(-1)^4+\dfrac{3}{2}\cdot(-1)^2+c&=&5 \\[5pt]
\dfrac{7}{2}+c&=&5 &\quad \scriptsize \; \bigg \vert\, \;-\dfrac{7}{2} \\[5pt]
c&=&\dfrac{3}{2}
\end{array}\)](https://mathjax.schullv.de/fd7200977f6f5a7c29ff0dfb9938b8434329c7c68662d38faff3b21ea8d39c90?color=5a5a5a)
Somit ist 
ein Funktionsterm der gesuchten Stammfunktion von 
2
a)
Der Graph 
die -Achse sowie die Geraden mit den Gleichungen 
und 
schließen eine Fläche ein, deren Teil unterhalb der -Achse einen kleineren Inhalt besitzt als deren Teil oberhalb.
Deshalb ist der Wert des Integrals nicht negativ.
b)
Ableitungsfunktion bilden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/6558829f2731f95fd9a159082201ac9f01e828fb8c4453ed3df238f2d62db5b0?color=5a5a5a)
Für die Tangente an 
im Koordinatenursprung gilt:
![\(\begin{array}[t]{rll}
m&=& f](https://mathjax.schullv.de/aa85a11e465168ec2ec5af2da2db7b3af8fdcb6a6d1e5555b8903c6cda0f53a6?color=5a5a5a)
Einsetzen der Koordinaten des Koordinatenursprungs sowie der Steigung 
in die allgemeine Tangente 
liefert:
![\(\begin{array}[t]{rll}
0&=& 1\cdot 0+n& \\[5pt]
0&=& n
\end{array}\)](https://mathjax.schullv.de/cd814f477868e5f3ee190659fc1fe911f32449c517ad8becf0edc8810958aa95?color=5a5a5a)
Ein Funktionsterm der Tangente ergibt sich also zu:
Die Gerade mit der Gleichung 
verläuft durch alle Punkte, deren -Koordinate mit ihrer 
-Koordinate übereinstimmt, und somit verläuft 
durch die Punkte 
und 
Damit trifft die Aussage zu.
3
a)
Da stets 
gilt, folgt für immer 
Somit verläuft der Graph von in diesem Fall unterhalb der -Achse.
b)
Für 
gilt:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to+\infty}f_a(x)&=&\left(\lim\limits_{x\to+\infty}x\right) \cdot \left(\lim\limits_{x\to+\infty}\mathrm e^{a\cdot x}\right) \\[5pt]
&=&(+\infty)\cdot(+\infty)\\[5pt]
&=&+\infty
\end{array}\)](https://mathjax.schullv.de/920377d22bf1ecccdf94fc665118715918f595c505384fb6bac01c2e9ceac945?color=5a5a5a)
Da die Funktion laut Aufgabenstellung für alle Werte von genau eine Extremstelle besitzt, fällt der Graph in Abbildung 1 für steigende Werte von weiter. Somit zeigt Abbildung 2 den Graphen der Schar mit positivem Wert von
4
a)
b)
Eine Möglichkeit, eine solche Funktion zu finden, ist eine Funktion zu betrachten, die genau für ![\(x\in[-2;4]\)](https://mathjax.schullv.de/d09604cbe2c9cfaa93b681a67c2165faed4a0ad9a760a24a3b07bf3c27a78499?color=5a5a5a)
größer oder gleich null ist und für alle weiteren Werte von negativ ist. Das ist möglich, indem die Funktion an den Stellen und 
Nullstellen besitzt, und nur im Bereich zwischen den beiden Nullstellen positive Werte annimmt. Ein möglicher Funktionsterm ist somit 
