Mathe Abi 2022: CAS & WTR Aufgaben zu Funktionen und Graphen

a)

Gegeben ist die Funktion $f: x\mapsto \frac{x^2 + 2x}{x+1}$ mit maximaler Definitionsmenge $D_f.$
Gib $D_f$ und die Nullstellen von $f$ an.

(2 BE)

b)

Gib einen Term einer gebrochen-rationalen Funktion $h$ an, die die folgenden Eigenschaften hat:
Die Funktion $h$ ist in $\mathbb{R}$ definiert; ihr Graph besitzt die Gerade mit der Gleichung $y=3$ als waagrechte Asymptote und schneidet die $y$ -Achse im Punkt $(0 \mid 4).$

(3 BE)

Gegeben ist die in $\mathbb{R}^+$ definierte Funktion $g: x\mapsto \frac{4}{x}.$ Abbildung 1 zeigt den Graphen von $g.$

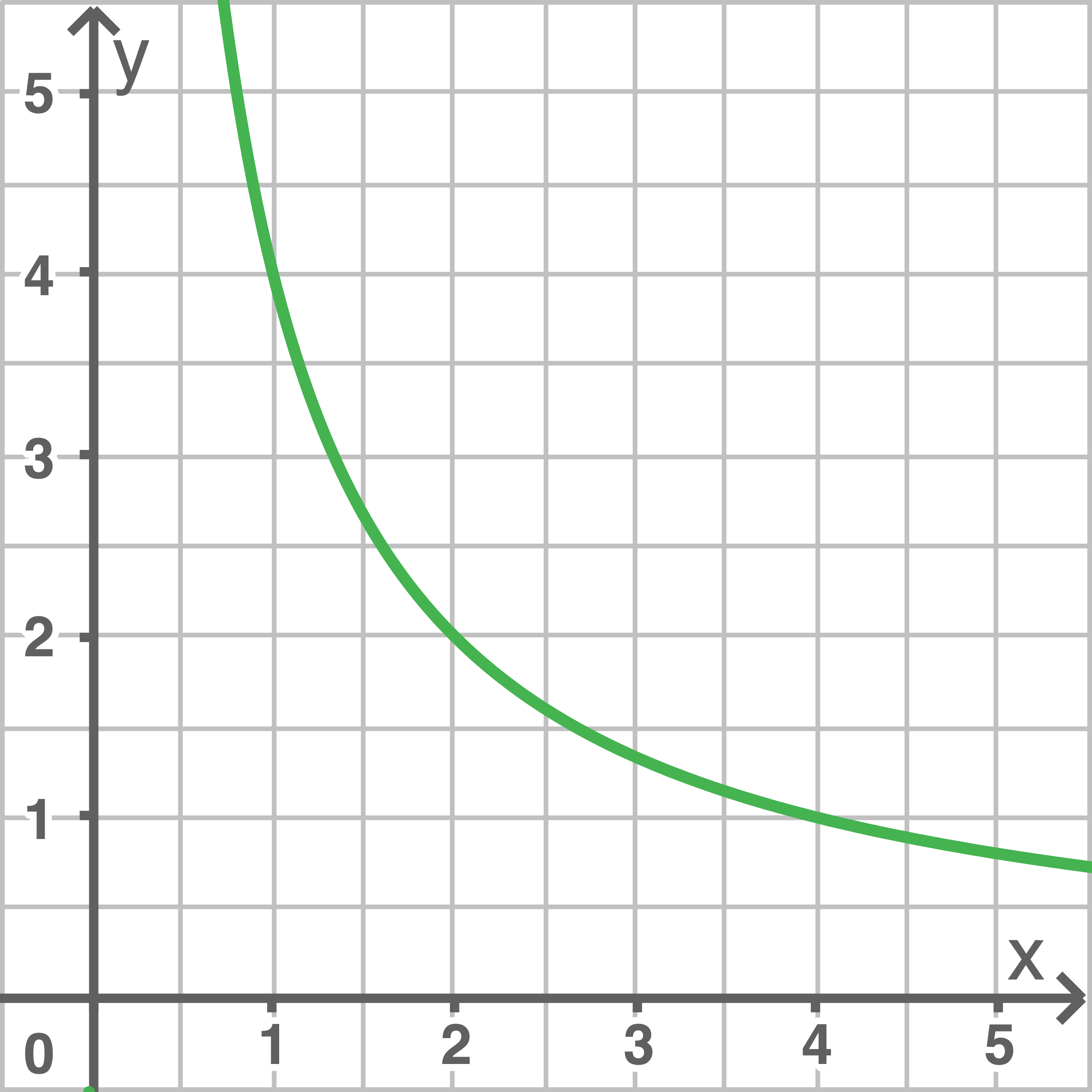
Abb. 1

a)

Berechne den Wert des Integrals $\displaystyle\int_{1}^{\mathrm e}g(x)\;\mathrm dx.$

(2 BE)

b)

Ermittle grafisch diejenige Stelle $x_0 \in \mathbb{R}^+$ , für die gilt:
Die lokale Änderungsrate von $g$ an der Stelle $x_0$ stimmt mit der mittleren Änderungsrate von $g$ im Intervall $[1;4]$ überein.

(3 BE)

Der Graph $G_f$ der in $\mathbb{R}$ definierten ganzrationalen Funktion $f$ besitzt nur an der Stelle $x=3$ eine waagrechte Tangente (vgl. Abbildung 2).
Betrachtet wird die in $\mathbb{R}$ definierte Funktion $g$ mit $g(x)= f (f(x)).$

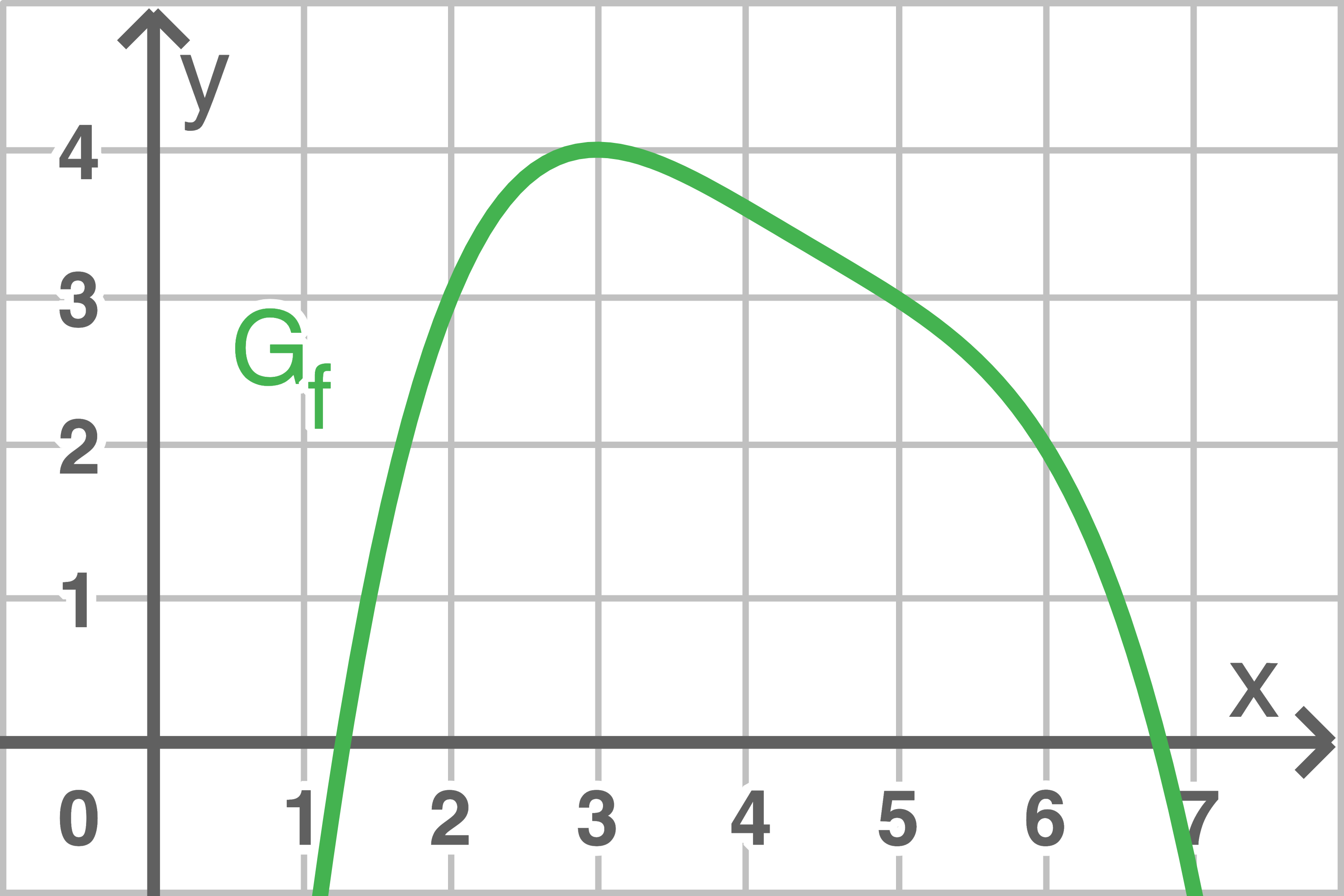
Abb. 2

a)

Gib mithilfe von Abbildung 2 die Funktionswerte $f(6)$ und $g(6)$ an.

(2 BE)

b)

Gemäß der Kettenregel gilt $\(g$
Ermittle damit und mithilfe von Abbildung 2 alle Stellen, an denen der Graph von $g$ eine waagrechte Tangente besitzt.

(3 BE)

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f_a$ mit $f_a(x)=a \cdot \mathrm e^{-x} + 3$ und $a \in \mathbb{R} \setminus\{ 0 \}.$

a)

Zeige, dass $\(f$ gilt.

(1 BE)

b)

Betrachtet wird die Tangente an den Graphen von $f_a$ im Punkt $(0 \mid f_a (0)).$
Bestimme diejenigen Werte von $a$ , für die diese Tangente eine positive Steigung hat und zudem die $x$ -Achse in einem Punkt schneidet, dessen $x$ -Koordinate größer als $\frac{1}{2}$ ist.

(4 BE)

Teil A

Weiter lernen mit SchulLV-PLUS!

Weiter lernen mit SchulLV-PLUS!