Geometrie Prüfungsteil A

Aufgabengruppe 1

1 Die Gerade $g$ verläuft durch die Punkte $A(0\mid1\mid2)$ und $B(2\mid5\mid6)$ .

a) Zeige, dass die Punkte $A$ und $B$ den Abstand $6$ haben.
Die Punkte $C$ und $D$ liegen auf $g$ und haben von $A$ jeweils den Abstand $12$ . Bestimme die Koordinaten von $C$ und $D$ .

(3P)

b) Die Punkte $A$ , $B$ und $E(1\mid2\mid5)$ sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunkts gibt es mehrere Möglichkeiten.
Gib für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunkts an.

(2P)

2 Betrachtet wird die Pyramide $ABCDS$ mit $A(0\mid0\mid0)$ , $B(4\mid4\mid2)$ , $C(8\mid0\mid2)$ , $D(4\mid-4\mid0)$ und $S(1\mid1\mid-4)$ . Die Grundfläche $ABCD$ ist ein Parallelogramm.

a) Weise nach, dass das Parallelogramm $ABCD$ ein Rechteck ist.

(2P)

b) Die Kante $[AS]$ steht senkrecht auf der Grundfläche $ABCD$ . Der Flächeninhalt der Grundfläche beträgt $24\sqrt{2}$ .
Ermittle das Volumen der Pyramide.

(3P)

(10P)

Aufgabengruppe 2

1 Die Gerade $g$ verläuft durch die Punkte $A(0\mid1\mid2)$ und $B(2\mid5\mid6)$ .

a) Zeige, dass die Punkte $A$ und $B$ den Abstand $6$ haben.
Die Punkte $C$ und $D$ liegen auf $g$ und haben von $A$ jeweils den Abstand $12$ . Bestimme die Koordinaten von $C$ und $D$ .

(3P)

(2P)

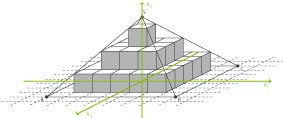
2 Die Abbildung zeigt die Pyramide $ABCDS$ mit quadratischer Grundfläche $ABCD$ . Der Pyramide ist eine Stufenpyramide einbeschrieben, die aus Würfeln mit der Kantenlänge 1 besteht.

3D-Darstellung einer Pyramide aus grauen Quadern mit einer Basis und mehreren Ebenen.

a) Gib das Volumen der Stufenpyramide und die Höhe der Pyramide $ABCDS$ an.

(2P)

b) Bestimme unter Verwendung eines geeignet gewählten kartesischen Koordinatensystems eine Gleichung für die Gerade, die durch die Punkte $B$ und $S$ verläuft.
Zeichne das gewählte Koordinatensystem in die Abbildung ein.

(3P)

(10P)

Aufgabengruppe 1

Aufgabe 1

a) $\blacktriangleright$ Zeigen, dass $\boldsymbol{A}$ und $\boldsymbol{B}$ den Abstand von 6 haben

Hier sollst du zeigen, dass die Punkte $A$ und $B$ einen Abstand von $6$ haben. Berechne dazu den Betrag des Vektors $\overrightarrow{AB}$ und zeige, dass dieser 6 beträgt.

$d = \left|\overrightarrow{OB} - \overrightarrow{OA}\right| = \left|\begin{pmatrix}2\\5\\6\end{pmatrix} - \begin{pmatrix}0\\1\\2\end{pmatrix}\right|$ $= \left|\begin{pmatrix}2\\4\\4\end{pmatrix}\right|$ $= \sqrt{2^2 + 4^2 + 4^2}$ $= \sqrt{4 + 2 \cdot 16} = \sqrt{36} = 6$

Damit hast du gezeigt, dass der Abstand zwischen $A$ und $B$ 6 ist.

$\blacktriangleright$ Bestimmen der Koordinaten der Punkte $\boldsymbol{C}$ und $\boldsymbol{D}$

Die Punkte $C$ und $D$ liegen auf der Geraden $g$ und besitzen einen Abstand von $12$ zum Punkt $A$ . Deine Aufgabe ist es hier die Koordinaten dieser Punkte zu bestimmen.
Willst du diese Aufgabe lösen, so definiere zunächst Gerade $g$ mit Aufpunkt $A$ und mit dem Richtungsvektor $\overrightarrow{AB}$ . Berechne anschließend die Koordinaten von $C$ und $D$ , indem du in Gerade $g$ die Werte $2$ und $-2$ einsetzt, da du oben gezeigt hast, dass $\overrightarrow{AB}$ die Länge 6 besitzt.

1. Schritt: Aufstellen der Geradengleichung von Gerade $\boldsymbol{g}$

Die Gleichung der Geraden $g$ ergibt sich zu:

$g: \vec{x} = \overrightarrow{OA} + t \cdot \overrightarrow{AB} = \begin{pmatrix}0 \\ 1 \\ 2\end{pmatrix} + t \cdot \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$

2. Schritt: Bestimmen der Koordinaten der Punkte $\boldsymbol{C}$ und $\boldsymbol{D}$

Setze nun $t = 2$ und $t = -2$ ein, um die Koordinaten der Punkte $C$ und $D$ zu bestimmen:

$\overrightarrow{OC} = \begin{pmatrix}0 \\ 1 \\ 2\end{pmatrix} + 2 \cdot \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$ $= \begin{pmatrix}4 \\ 9 \\ 10\end{pmatrix}$

$\overrightarrow{OD} = \begin{pmatrix}0 \\ 1 \\ 2\end{pmatrix} - 2 \cdot \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$ $= \begin{pmatrix}-4 \\ -7 \\ -6\end{pmatrix}$

Die Koordinaten der Punkte $C$ und $D$ sind: $C(4 \mid 9 \mid 10)$ und $D(-4 \mid -7 \mid -6)$ .

b) $\blacktriangleright$ Möglichkeiten für den vierten Eckpunkt angeben

Der Aufgabenstellung kannst du nun entnehmen, dass $A$ , $B$ sowie $E$ , mit $E(1 \mid 2 \mid 5)$ , mit einem weiteren Punkt, die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten gesuchten Eckpunkts gibt es mehrere Möglichkeiten. Deine Aufgabe ist es nun, zwei Mögliche Koordinaten für diesen Punkt $F$ anzugeben.
Hier bietet es sich an, eine zweidimensionale Skizze für den Sachverhalt anzufertigen, indem beide mögliche Positionen für $F$ eingezeichnet sind:

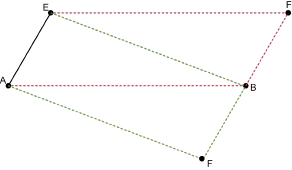Diagramm eines geometrischen Problems mit Punkten A, B, E und F sowie Linien zwischen ihnen.

Berechne nun ausgehende von dieser Skizze mit Hilfe der Vektorverkettung zwei mögliche Koordinaten für $F$ .

Die ersten mögliche Koordinaten von $F$ ergibt sich über die Vektorensumme von $\overrightarrow{OE}$ und $\overrightarrow{AB}$

$\overrightarrow{OF} = \begin{pmatrix}1 \\ 2 \\ 5\end{pmatrix} + \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$ $= \begin{pmatrix}3 \\ 6 \\ 9\end{pmatrix}$ .

Die zweiten möglichen Koordinaten von $F$ ergibt sich über die Vektorensumme von $\overrightarrow{OB}$ und $\overrightarrow{OF}$ :

$\overrightarrow{OF} = \begin{pmatrix}2 \\ 5 \\ 6\end{pmatrix} + \left(\begin{pmatrix}0 \\ 1 \\ 2\end{pmatrix} - \begin{pmatrix}1 \\ 2 \\ 5\end{pmatrix}\right)$ $= \begin{pmatrix}2 \\ 5 \\ 6\end{pmatrix} + \begin{pmatrix}-1 \\ - 1 \\ - 3\end{pmatrix}$ $= \begin{pmatrix}1 \\ 4 \\ 3\end{pmatrix}$ .

Mögliche Koordinaten für $F$ sind also:

$F(3 \mid 6 \mid 9)$

$F(1 \mid 4 \mid 3)$

Aufgabe 2

a) $\blacktriangleright$ Nachweisen, dass das Parallelogramm $\boldsymbol{ABCD}$ ein Rechteck ist

Willst du nachweisen, dass das Parallelogramm $ABCD$ ein Reckteck darstellt, so musst du nachweisen, dass dieses vier rechte Winkel besitzt.
Besitzt ein Viereck insgesamt 2 rechte Winkel, so kann man sofort folgern, dass es vier rechte Winkel besitzt.
Zeige hier also, dass das Viereck $ABCD$ zwei rechte Winkel besitzt, um zu zeigen, dass es ein Reckteck ist. Willst du nachweisen, dass zwei Seiten im rechten Winkel aufeinander stehen, so musst du zeigen, dass das Skalarprodukt der zugehörigen Vektoren Null ist.

$\overrightarrow{AB} \circ \overrightarrow{BC} = \left(\begin{pmatrix}4 \\ 4 \\ 2\end{pmatrix} - \begin{pmatrix}0 \\ 0 \\ 0\end{pmatrix}\right) \circ \left(\begin{pmatrix}8 \\ 0 \\ 2\end{pmatrix} - \begin{pmatrix}4 \\ 4 \\ 2\end{pmatrix}\right)$ $= \begin{pmatrix}4 \\ 4 \\ 2\end{pmatrix} \circ \begin{pmatrix}4 \\ -4 \\ 0\end{pmatrix}$ $= 4 \cdot 4 + 4 \cdot (-4) + 2 \cdot 0 = 16 - 16 = 0$

$\overrightarrow{BC} \circ \overrightarrow{CD} =\begin{pmatrix}4 \\ -4 \\ 0\end{pmatrix} \circ \left(\begin{pmatrix}4 \\ -4 \\ 0\end{pmatrix} - \begin{pmatrix}8 \\ 0 \\ 2\end{pmatrix}\right)$ $= \begin{pmatrix}4 \\ -4 \\ 0\end{pmatrix} \circ \begin{pmatrix}- 4 \\ -4 \\ -2\end{pmatrix}$ $= (-4) \cdot 4 + (-4) \cdot (-4) + (-2) \cdot 0$ $= -16 + 16 = 0$

Da du so gezeigt hast, dass zwei Seiten des Parallelogramms $ABCD$ im rechten Winkel aufeinander stehen, hast du gezeigt, dass es sich bei diesem um ein Rechteck handelt.

b) $\blacktriangleright$ Berechnen des Volumens der Pyramide

Der Aufgabenstellung kannst du entnehmen, dass die Kante $[AS]$ senkrecht auf der Grundfläche $ABCD$ steht. Der Flächeninhalt der Grundfläche beträgt dabei $24\cdot \sqrt{2}$ .
Da die Strecke $[AS]$ senkrecht auf der Grundfläche der Pyramiden steht kann diese als Höhe $h$ der Pyramide angenommen werden. Das Volumen $V$ einer Pyramiden berechnet sich dabei über folgende Formel:

$V = \frac{1}{3} \cdot G \cdot h$

Dabei handelt es sich bei $G$ um die Grundfläche und $h$ um die Höhe der Pyramide. Berechne also zuvor die Länge der Höhe $h$ über den Betrag des Vektors $\overrightarrow{AS}$ .

1. Schritt: Berechnen der Höhe $\boldsymbol{h}$

Die Höhe $h$ berechnet sich mit Hilfe des Betrages wie folgt:

$h = \left|\begin{pmatrix}1 \\ 1 \\ -4\end{pmatrix} - \begin{pmatrix}0 \\ 0 \\ 0\end{pmatrix}\right|$ $=\left|\begin{pmatrix}1 \\ 1 \\ -4\end{pmatrix}\right|$ $= \sqrt{1^2 + 1^2 + (-4)^2}$ $= \sqrt{18} = 3 \cdot \sqrt{2}$

2. Schritt: Berechnen des Volumens $\boldsymbol{V}$

Durch Einsetzen ergibt sich hier:

$V = \dfrac{1}{3} \cdot 24\cdot \sqrt{2} \cdot 3 \cdot \sqrt{2} = 48\,\text{VE}$

Das Volumen der Pyramiden beträgt $48\,\text{VE}$ .

Aufgabengruppe 2

Aufgabe 1

a) $\blacktriangleright$ Zeigen, dass $\boldsymbol{A}$ und $\boldsymbol{B}$ den Abstand von 6 haben

Hier sollst du zeigen, dass die Punkte $A$ und $B$ einen Abstand von $6$ haben. Berechne dazu den Betrag des Vektors $\overrightarrow{AB}$ und zeige, dass dieser 6 beträgt.

$d = \left|\overrightarrow{OB} - \overrightarrow{OA}\right|$ $= \left|\begin{pmatrix}2\\5\\6\end{pmatrix} - \begin{pmatrix}0\\1\\2\end{pmatrix}\right|$ $= \left|\begin{pmatrix}2\\4\\4\end{pmatrix}\right|$ $= \sqrt{2^2 + 4^2 + 4^2}$ $= \sqrt{4 + 2 \cdot 16} = \sqrt{36} = 6$

Damit hast du gezeigt, dass der Abstand zwischen $A$ und $B$ 6 ist.

$\blacktriangleright$ Bestimmen der Koordinaten der Punkte $\boldsymbol{C}$ und $\boldsymbol{D}$

1. Schritt: Aufstellen der Geradengleichung von Gerade $\boldsymbol{g}$

Die Gleichung der Geraden $g$ ergibt sich zu:

$g: \vec{x} = \overrightarrow{OA} + t \cdot \overrightarrow{AB}$ $= \begin{pmatrix}0 \\ 1 \\ 2\end{pmatrix} + t \cdot \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$

2. Schritt: Bestimmen der Koordinaten der Punkte $\boldsymbol{C}$ und $\boldsymbol{D}$

Setze nun $t = 2$ und $t = -2$ ein, um die Koordinaten der Punkte $C$ und $D$ zu bestimmen:

$\overrightarrow{OC} = \begin{pmatrix}0 \\ 1 \\ 2\end{pmatrix} + 2 \cdot \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$ $= \begin{pmatrix}4 \\ 9 \\ 10\end{pmatrix}$

$\overrightarrow{OD} = \begin{pmatrix}0 \\ 1 \\ 2\end{pmatrix} - 2 \cdot \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$ $= \begin{pmatrix}-4 \\ -7 \\ -6\end{pmatrix}$

Die Koordinaten der Punkte $C$ und $D$ sind: $C(4 \mid 9 \mid 10)$ und $D(-4 \mid -7 \mid -6)$ .

b) $\blacktriangleright$ Möglichkeiten für den vierten Eckpunkt angeben

Der Aufgabenstellung kannst du nun entnehmen, dass $A$ , $B$ sowie $E$ , mit $E(1 \mid 2 \mid 5)$ , mit einem weiteren Punkt, die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten gesuchten Eckpunkts gibt es mehrere Möglichkeiten. Deine Aufgabe ist es nun, zwei mögliche Koordinaten für diesen Punkt $F$ anzugeben.
Hier bietet es sich an, eine zweidimensionale Skizze für den Sachverhalt anzufertigen, indem beide mögliche Positionen für $F$ eingezeichnet sind:

Berechne nun ausgehende von dieser Skizze mit Hilfe der Vektorverkettung zwei mögliche Koordinaten für $F$ .

Die erste Möglichkeit für die Koordinaten von $F$ ergibt sich über die Vektorensumme von $\overrightarrow{OE}$ und $\overrightarrow{AB}$

$\overrightarrow{OF} = \begin{pmatrix}1 \\ 2 \\ 5\end{pmatrix} + \begin{pmatrix}2 \\ 4 \\ 4\end{pmatrix}$ $= \begin{pmatrix}3 \\ 6 \\ 9\end{pmatrix}$ .

Die zweite Möglichkeit für die Koordinaten von $F$ ergibt sich über die Vektorensumme von $\overrightarrow{OB}$ und $\overrightarrow{OF}$ :

Mögliche Koordinaten für $F$ sind also:

$F(3 \mid 6 \mid 9)$

$F(1 \mid 4 \mid 3)$

Aufgabe 2

a) $\blacktriangleright$ Berechnen des Volumens der Stufenpyramide

Du sollst nun das Volumen der Stufenpyramide berechnen, die in die Pyramide $ABCDS$ einbeschrieben ist. Die Kantenlänge der Würfel beträgt 1.

Die unterste Schicht der Stufenpyramide besteht aus 5 Reihen, die jeweils aus 5 Würfeln bestehen. Die zweite Schicht besteht aus 3 Reihen, die jeweils aus 3 Würfeln besteht. Die oberste Schicht besteht aus einem Würfel.

Um das Volumen zu berechnen musst du also die Anzahl der Würfel mit ihrem Volumen multiplizieren.

Das Volumen eines Würfels mit Kantenlänge $a$ berechnet sich mit folgender Formel

$V_{\text{Würfel}}=a^3$

Das Volumen eines Würfels beträgt $V_{\text{Würfel}} = 1 \cdot 1 \cdot 1 = 1 \text{ VE}$ .

Das Volumen der Stufenpyramide setzt sich also folgendermaßen zusammen:

$\begin{array}[t]{rll} V&=& (5 \cdot 5 + 3 \cdot 3 + 1) \cdot V_{\text{Würfel}}\\[5pt] &=&35 \text{ VE} \end{array}$

Das Volumen der Stufenpyramide beträgt 35 VE.

$\blacktriangleright$ Berechnen der Höhe

Jetzt sollst du die Höhe der Pyramide $ABCDS$ bestimmen. Betrachte dafür die Hälfte eines Querschnitts der Pyramide. Wie in der Abbildung gezeigt, hat jede Kante des Würfels eine Länge von 1.

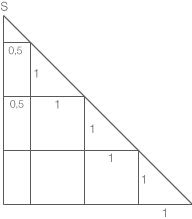Diagramm mit einem rechtwinkligen Dreieck und unterteilten Bereichen, beschriftet mit Zahlen.

Die Steigung der Gerade, die die Höhe der Seitenfläche darstellt, kannst du mithilfe des Steigungsdreiecks berechnen.

$m = \dfrac{\Delta y}{\Delta x}$

Somit ergibt sich für die Steigung: $m = 1$ .

In die Pyramide passen 3 Schichten der Würfel, berechne die Höhe der Stufenpyramide.

Dann fehlt dir noch der Abstand zwischen der Stufenpyramide und der Spitze $S$ . Die Gerade, die die Seitenfläche darstellt, hat eine Steigung von 1 und die oberste Schicht der Pyramide besteht aus einem Würfel, somit ist $\Delta x = 0,5$ und für $\Delta y$ gilt:

$\begin{array}[t]{rll} 1&=& \dfrac{\Delta y}{0,5}\quad \scriptsize \mid\; \cdot 0,5\\[5pt] \Delta y&=&0,5 \end{array}$

Jetzt kannst du die Höhe der Pyramide berechnen:

$h = 3 + 0,5 = 3,5$ .

Die Höhe der Pyramide $ABCDS$ beträgt 3,5 LE.

b) $\blacktriangleright$ Geradengleichung aufstellen

Du sollst ein geeignetes Koordinatensystem aufstellen, um dann die Geradengleichung der Gerade, die durch $B$ und $S$ verläuft, aufzustellen.

Wähle hierzu als Koordinatenursprung den Mittelpunkt der quadratischen Grundfläche der Pyramide. Die Spitze $S$ der Pyramide liegt dann 3,5 Einheiten oberhalb des Ursprungs, hat also folgende Koordinaten:

$S(0 \mid 0 \mid 3,5)$

Der Punkt $B$ ist vom Koordinatenursprung 3,5 Einheiten in positive $x_1$ -Richtung und 3,5 Einheiten in positive $x_2$ -Richtung verschoben. Die Koordinaten lauten dann

$B(3,5 \mid 3,5 \mid 0)$

Nun kannst du die Geradengleichung aufstellen, verwende hierfür $B$ als Aufpunkt und $\overrightarrow{BS}$ als Richtungsvektor:

$\begin{array}[t]{rll} g: \quad \vec{x}&=&\overrightarrow{OB} + r \cdot \overrightarrow{BS} \\[5pt] &=&\begin{pmatrix}3,5 -0 \\3,5 -0\\0-0\end{pmatrix} + r \cdot \begin{pmatrix}0-3,5 \\0-3,5\\3,5-0\end{pmatrix}\\[5pt] &=&\begin{pmatrix}3,5\\3,5\\0\end{pmatrix} + r \cdot \begin{pmatrix}-3,5 \\-3,5\\3,5\end{pmatrix} \end{array}$

$\blacktriangleright$ Koordinatensystem einzeichnen

Nun sollst du noch das gewählte Koordinatensystem in die Abbildung der Pyramide einzeichnen. Zeichne hierfür die $x_3$ -Achse senkrecht durch den Punkt $S$ . Die $x_2$ -Achse befindet sind in der Mitte zwischen Punkt $B$ und $C$ , im rechten Winkel zur $x_3$ -Achse. Die $x_1$ -Achse befindet sind in der Mitte zwischen Punkt $A$ und $B$ , ca. im 45° Winkel zur $x_2$ -Achse.

3D-Darstellung einer pyramidenförmigen Struktur mit Koordinatensystem.