Teil B
1
Gegeben ist die Funktion  mit maximalem Definitionsbereich
mit maximalem Definitionsbereich  Ihr Graph wird mit
Ihr Graph wird mit  bezeichnet.
bezeichnet.
![\(k \in] 0 ; 5[\)](https://www.schullv.de/api/node/mathjax-to-svg/96773de8c9fa53ed3b901805a139e26a88c26f9783349689928bea16e654e9f1?color=5a5a5a) schließen
schließen  und die
und die  -Achse ein Dreieck ein, dessen Flächeninhalt durch die in
-Achse ein Dreieck ein, dessen Flächeninhalt durch die in ![\(]0;5[\)](https://www.schullv.de/api/node/mathjax-to-svg/5eb96ef6f824de3ec8f723f9fbec9a15d67aa6c5c2fe306238b8649db51376d8?color=5a5a5a) definierte Funktion
definierte Funktion  beschrieben wird.
beschrieben wird.
a)
Gib  und die Nullstellen von
und die Nullstellen von  an.
an.
(2 BE)
b)
Zeige rechnerisch, dass jeder Punkt auf  den gleichen Abstand zum Koordinatenursprung hat.
den gleichen Abstand zum Koordinatenursprung hat.
(2 BE)
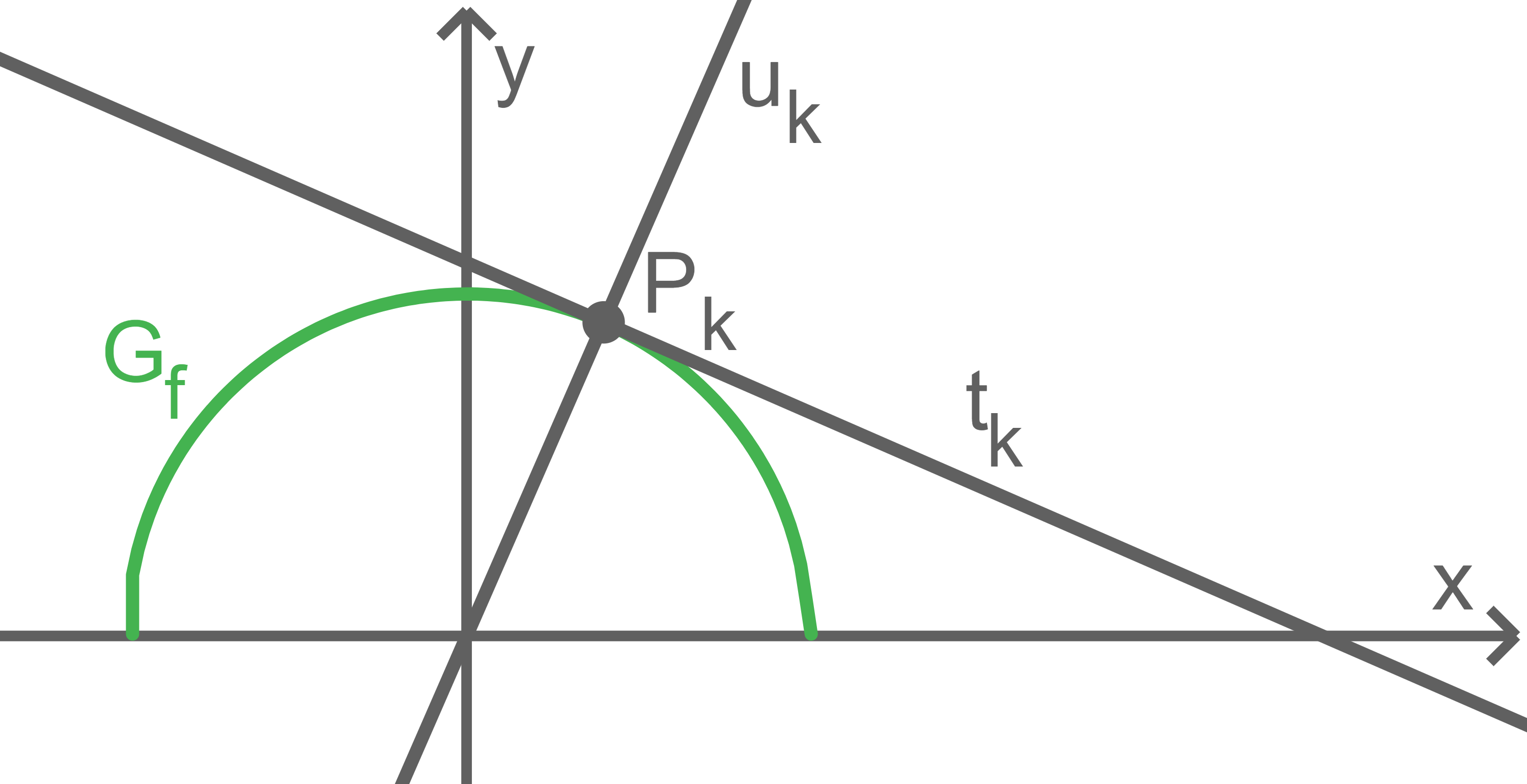
Der Graph  ist ein Halbkreis. Für
ist ein Halbkreis. Für ![\(k \in] 0 ; 5 [\)](https://www.schullv.de/api/node/mathjax-to-svg/94aa62080682ea96b4d5daa0cb6eddfd9eaa9c06c4283ed5f0adb00162ac3dcc?color=5a5a5a) wird die Tangente an
wird die Tangente an  im Punkt
im Punkt  mit
mit  bezeichnet und die Ursprungsgerade durch
bezeichnet und die Ursprungsgerade durch  mit
mit  (vgl. Abbildung 1).
(vgl. Abbildung 1).

Abb. 1
c)
Bestimme denjenigen Wert von  für den die Tangente
für den die Tangente  mit der
mit der  -Achse einen Winkel mit einer Größe von
-Achse einen Winkel mit einer Größe von  einschließt.
einschließt.
(2 BE)
d)
Weise rechnerisch nach, dass  und
und  zueinander senkrecht stehen.
zueinander senkrecht stehen.
Für jeden Wert
(3 BE)
e)
Begründe geometrisch, dass  und
und  gilt.
gilt.
(3 BE)
f)
Weise nach, dass  ein Term von
ein Term von  ist.
ist.
(4 BE)
g)
Zeige, dass  in
in ![\(] 0 ; 5[\)](https://www.schullv.de/api/node/mathjax-to-svg/ef7afad31224d09bb5d23b1fc339f158858e75a6fd250331dd075dabca5b9d93?color=5a5a5a) streng monoton abnimmt und genau eine Wendestelle besitzt. Gib diese Wendestelle und ihre Bedeutung für den von
streng monoton abnimmt und genau eine Wendestelle besitzt. Gib diese Wendestelle und ihre Bedeutung für den von  abhängigen Flächeninhalt des Dreiecks an.
abhängigen Flächeninhalt des Dreiecks an.
(4 BE)
2
Betrachtet wird die Funktion  mit maximalem Definitionsbereich und
mit maximalem Definitionsbereich und ![\(b \in] 0 ; 5[.\)](https://www.schullv.de/api/node/mathjax-to-svg/e0c283145c94d389a2a26e451fa2201795f015375884b0cfe002083a17eb208c?color=5a5a5a)
 mit
mit ![\(a \in[-2 ; 8]\)](https://www.schullv.de/api/node/mathjax-to-svg/5a72af06355d8b84d17eca7caed50425366090031a9066c5ff9b605978135240?color=5a5a5a) entsprechen den Positionen des Planeten auf dem modellierten Teil seiner Bahn.
entsprechen den Positionen des Planeten auf dem modellierten Teil seiner Bahn.
Für die Bewegung des Planeten gilt im Modell: Die Strecke![\([OB_a]\)](https://www.schullv.de/api/node/mathjax-to-svg/33b331080d5228e244722f4271de84fbaee3885503548d78d51af6cc20df6875?color=5a5a5a) überstreicht in gleichen Zeitabschnitten Flächenstücke gleich großen Inhalts.
überstreicht in gleichen Zeitabschnitten Flächenstücke gleich großen Inhalts.
a)
Beschreibe, wie der Graph von  aus dem Graphen
aus dem Graphen  aus Aufgabe 1 hervorgeht, und gib die Wertemenge von
aus Aufgabe 1 hervorgeht, und gib die Wertemenge von  in Abhängigkeit von
in Abhängigkeit von  an.
an.
(2 BE)
b)
Der Graph von  schließt mit der
schließt mit der  -Achse ein Flächenstück ein. Zeige, dass dieses Flächenstück den Inhalt
-Achse ein Flächenstück ein. Zeige, dass dieses Flächenstück den Inhalt  hat.
hat.
(2 BE)
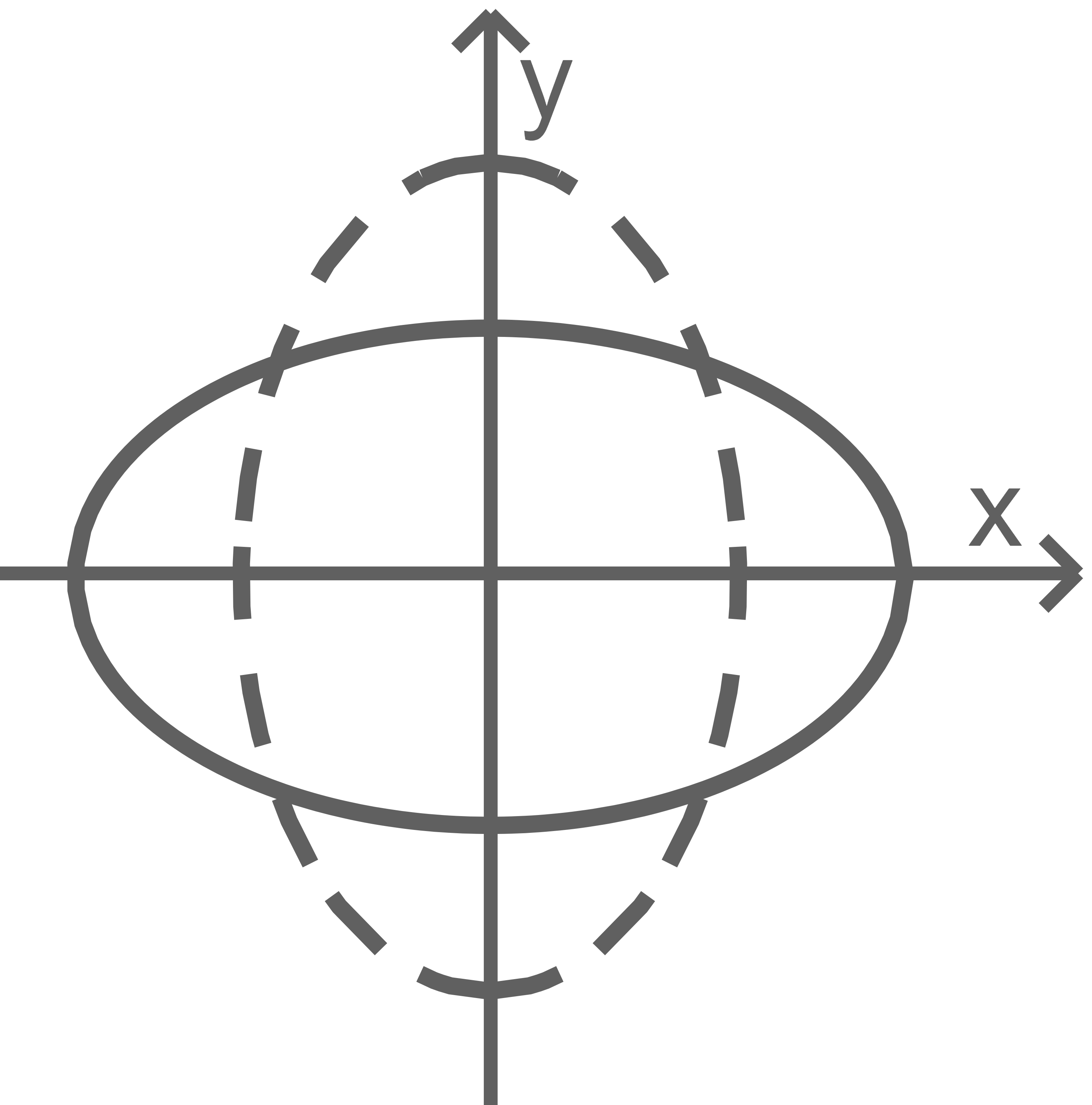
Der Graph von  geht durch Spiegelung an der
geht durch Spiegelung an der  -Achse in den Graphen der Funktion
-Achse in den Graphen der Funktion  über. Die Graphen von
über. Die Graphen von  und
und  bilden zusammen eine Ellipse, die beispielhaft für einen bestimmten Wert von
bilden zusammen eine Ellipse, die beispielhaft für einen bestimmten Wert von  in Abbildung 2 als durchgezogene Linie dargestellt ist.
in Abbildung 2 als durchgezogene Linie dargestellt ist.

Abb. 2
c)
Gib einen Funktionsterm von  an.
an.
(1 BE)
d)
Durch eine  -Drehung der Ellipse um den Koordinatenursprung entsteht eine weitere Ellipse, die in Abbildung 2 als gestrichelte Linie dargestellt ist. Ermittle einen Term einer Funktion, deren Graph im ersten Quadranten mit dieser weiteren Ellipse übereinstimmt.
-Drehung der Ellipse um den Koordinatenursprung entsteht eine weitere Ellipse, die in Abbildung 2 als gestrichelte Linie dargestellt ist. Ermittle einen Term einer Funktion, deren Graph im ersten Quadranten mit dieser weiteren Ellipse übereinstimmt.
(3 BE)
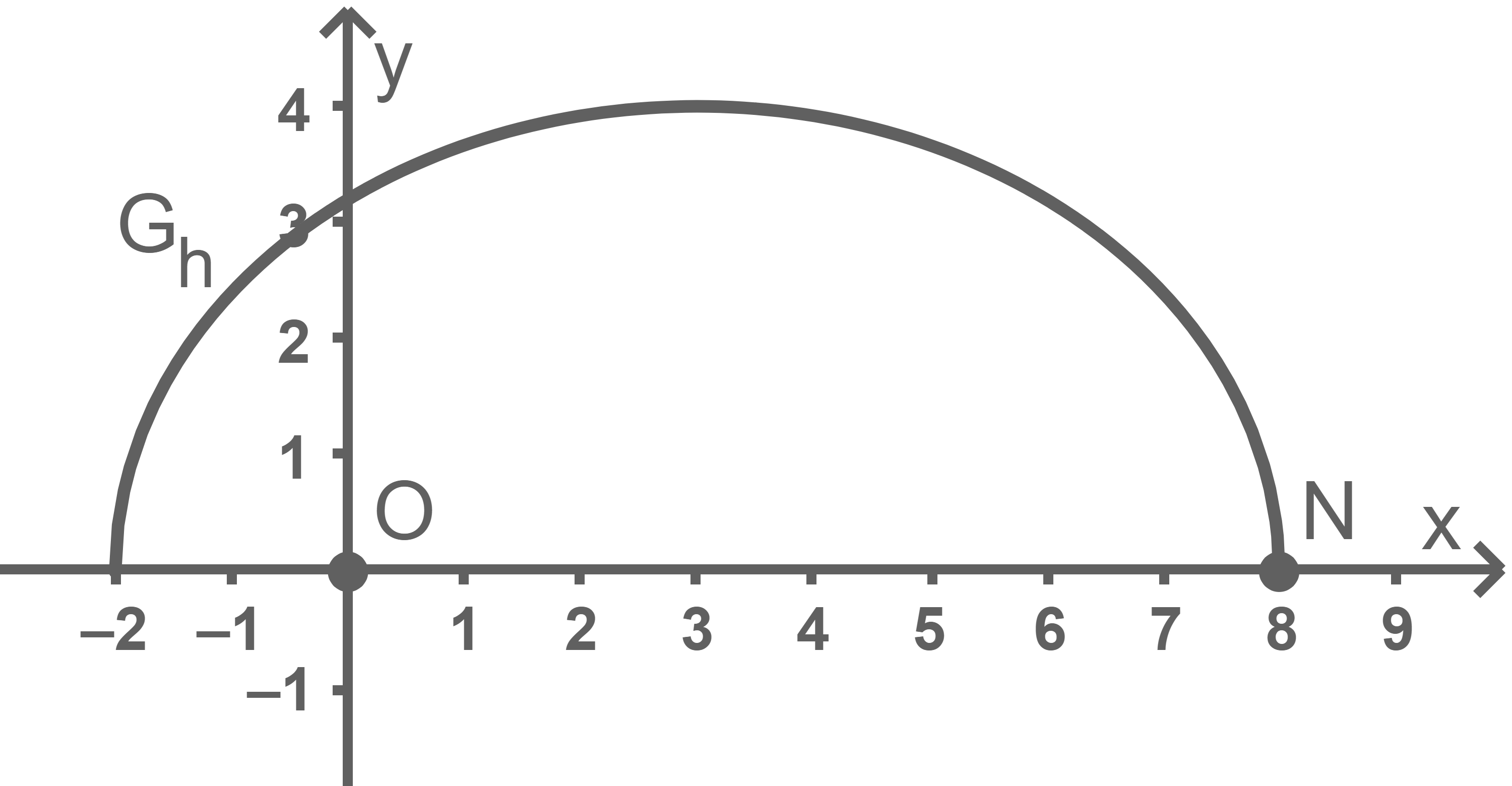
In einem bestimmten Planetensystem bewegt sich ein Planet auf einer elliptischen Bahn um einen Stern. Der Graph  der in
der in ![\([-2;8]\)](https://www.schullv.de/api/node/mathjax-to-svg/3d804ec0361c0b9b2011b858d45949df620367f8542fd8d65ef3f1918010df07?color=5a5a5a) definierten Funktion
definierten Funktion 
 beschreibt modellhaft einen Teil dieser Bahn. In diesem Modell entspricht die Position des Sterns dem Koordinatenursprung
beschreibt modellhaft einen Teil dieser Bahn. In diesem Modell entspricht die Position des Sterns dem Koordinatenursprung  und die Position, an der der Planet den größten Abstand vom Stern besitzt, dem Punkt
und die Position, an der der Planet den größten Abstand vom Stern besitzt, dem Punkt  (vgl. Abbildung 3).
(vgl. Abbildung 3).

Abb. 3
e)
Weise rechnerisch nach, dass  aus dem Graphen der Funktion
aus dem Graphen der Funktion  durch Verschiebung um
durch Verschiebung um  in positive
in positive  -Richtung hervorgeht.
-Richtung hervorgeht.
Die Punkte
(1 BE)
Für die Bewegung des Planeten gilt im Modell: Die Strecke
Das bedeutet für ![\(a_1, a_2, a_3, a_4 \in[-2 ; 8]\)](https://www.schullv.de/api/node/mathjax-to-svg/9704c55e837e709f9807edf205c70808f8434282a87a3fb4fac9a103084eaf7f?color=5a5a5a) mit
mit  und
und  Wenn der Planet für den Bahnabschnitt, der im Modell durch die Punkte
Wenn der Planet für den Bahnabschnitt, der im Modell durch die Punkte  und
und  begrenzt wird, die gleiche Zeit benötigt wie für den Bahnabschnitt, der durch die Punkte
begrenzt wird, die gleiche Zeit benötigt wie für den Bahnabschnitt, der durch die Punkte  und
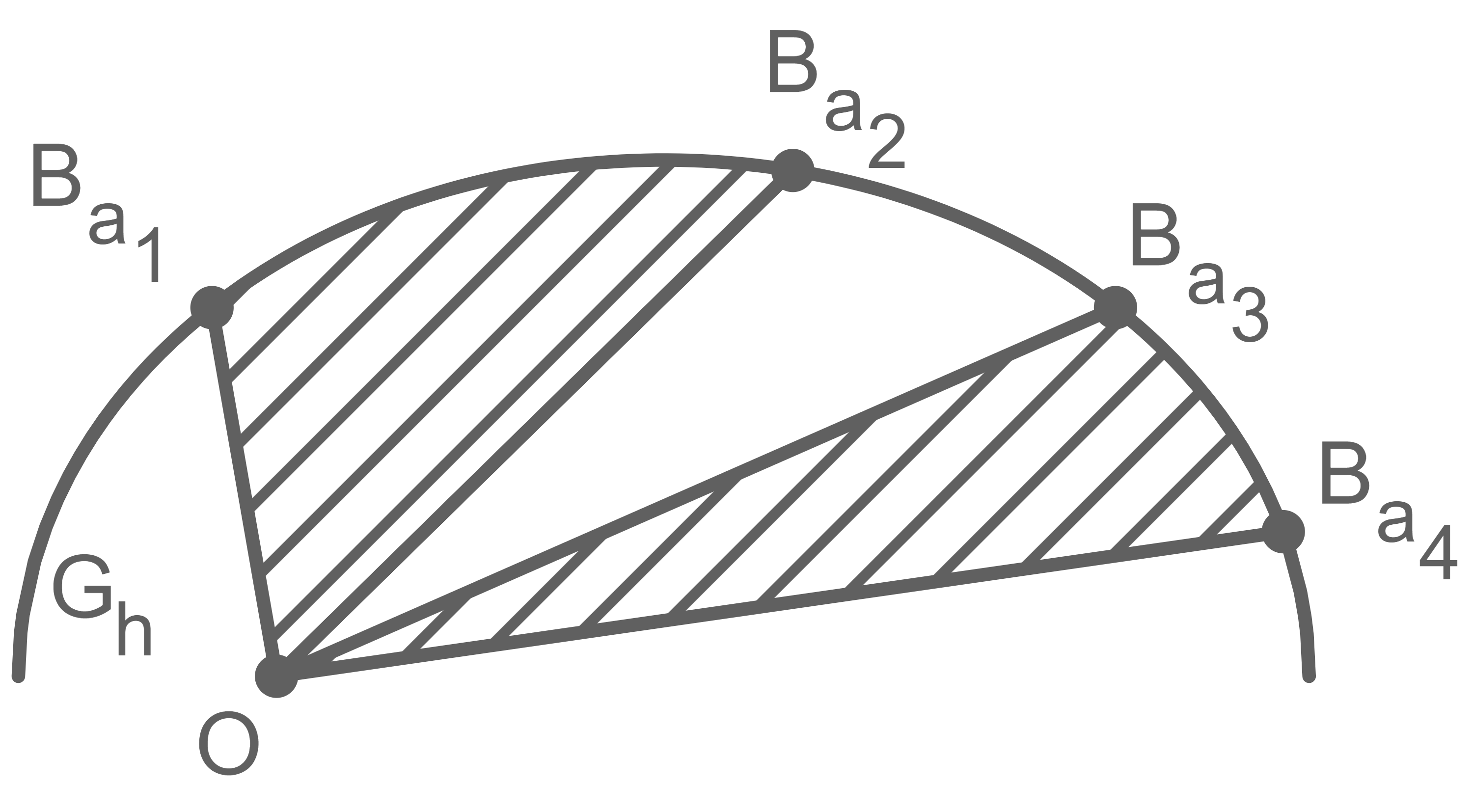
und  begrenzt wird, so hat das Flächenstück, das von
begrenzt wird, so hat das Flächenstück, das von ![\(G_h,[OB_{a_1}]\)](https://www.schullv.de/api/node/mathjax-to-svg/b61a38a47fafb6df179884e8cdcb9d0cb5b26e92d256b853c1fa72bd2f29465e?color=5a5a5a) und
und ![\([OB_{a_2}]\)](https://www.schullv.de/api/node/mathjax-to-svg/7a52d63868f5cb35b572ed69fcf59ac669361b23e8d49176504dc98027a0202a?color=5a5a5a) eingeschlossen wird, den gleichen Inhalt wie das Flächenstück, das von
eingeschlossen wird, den gleichen Inhalt wie das Flächenstück, das von ![\(G_h,[OB_{a_3}]\)](https://www.schullv.de/api/node/mathjax-to-svg/1641caf21c12ef27ee7147ea69dbbdd7dd7c5026488f7819d84b1043035b628c?color=5a5a5a) und
und ![\([OB_{a_4}]\)](https://www.schullv.de/api/node/mathjax-to-svg/461f8cb24410f7fc6a900f70396f9e536bab6f6b769e7c001d48205416c29219?color=5a5a5a) eingeschlossen wird (vgl. Abbildung 4).
eingeschlossen wird (vgl. Abbildung 4).

Abb. 4
f)
Es gibt einen Wert  , für den das von
, für den das von ![\(G_h,[OB_{a^*}]\)](https://www.schullv.de/api/node/mathjax-to-svg/fab6cd7d1b89850d9bc1645f2100db007973b61f5ee69f4af81939e7cca2ff66?color=5a5a5a) und
und ![\([ON]\)](https://www.schullv.de/api/node/mathjax-to-svg/56450a6756682b8b12cdbb180e3831048c439d5734f5a0d6d835689f8a043d63?color=5a5a5a) eingeschlossene Flächenstück den gleichen Inhalt hat wie das Flächenstück, das
eingeschlossene Flächenstück den gleichen Inhalt hat wie das Flächenstück, das  im zweiten Quadranten mit den Koordinatenachsen einschließt. Ermittle diesen Wert
im zweiten Quadranten mit den Koordinatenachsen einschließt. Ermittle diesen Wert 
(zur Kontrolle:  )
)
(4 BE)
g)
Zeichne den Punkt  in Abbildung 3 ein. Begründe anhand von Abbildung 3, dass die mittlere Bahngeschwindigkeit des Planeten in dem Bahnabschnitt, der im Modell im zweiten Quadranten durch die Schnittpunkte von
in Abbildung 3 ein. Begründe anhand von Abbildung 3, dass die mittlere Bahngeschwindigkeit des Planeten in dem Bahnabschnitt, der im Modell im zweiten Quadranten durch die Schnittpunkte von  mit den Koordinatenachsen begrenzt wird, größer ist als die mittlere Bahngeschwindigkeit des Planeten auf dem im Modell durch
mit den Koordinatenachsen begrenzt wird, größer ist als die mittlere Bahngeschwindigkeit des Planeten auf dem im Modell durch  und
und  im ersten Quadranten begrenzten Bahnabschnitt.
im ersten Quadranten begrenzten Bahnabschnitt.
(4 BE)
h)
Der Planet benötigt für den in Aufgabe 2g beschriebenen Bahnabschnitt, der im Modell im zweiten Quadranten liegt, drei Tage. Berechne die Zeit, die der Planet für einen vollständigen Umlauf um den Stern benötigt.
(3 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Da die Wurzelfunktion nur für nichtnegative Zahlen definiert ist, gilt 
![\( = [-5;5].\)](https://www.schullv.de/api/node/mathjax-to-svg/5f06e3a4886822315b04e463a4b053c5a615312b5f07a15a7442e2431a0fe52f?color=5a5a5a) Auf diese Weise ergeben sich auch die Nullstellen von
Auf diese Weise ergeben sich auch die Nullstellen von  zu
zu  und
und 
b)
Für den Abstand  eines Punkts
eines Punkts  zum Koordinatenursprung gilt:
zum Koordinatenursprung gilt:
![\(\begin{array}[t]{rll}
d(x) &=& \sqrt{x^2 +f(x)^2} \\[5pt]
&=& \sqrt{x^2+\sqrt{25-x^2}^2} \\[5pt]
&=& \sqrt{x^2 + 25 -x^2} \\[5pt]
&=& 5
\end{array}\)](https://www.schullv.de/api/node/mathjax-to-svg/50fe906ae1bc40b628cd7fd2311f54951d11884e7ded48c9ded06fa95b17aaa5?color=5a5a5a) Jeder Punkt auf
Jeder Punkt auf  hat also den Abstand
hat also den Abstand  zum Koordinatenursprung.
zum Koordinatenursprung.
c)
Ableiten von  im CAS liefert folgenden Funktionsterm:
im CAS liefert folgenden Funktionsterm:
 Die Steigung
Die Steigung  der Tangenten
der Tangenten  ist somit gegeben durch
ist somit gegeben durch 
 Es folgt:
Es folgt:
 Mit dem solve-Befehl des CAS folgt weiter:
Mit dem solve-Befehl des CAS folgt weiter:

d)
Für die Steigung  der Geraden
der Geraden  folgt mit dem Differenzenquotienten:
folgt mit dem Differenzenquotienten:


 Mit der Steigung von
Mit der Steigung von  aus Aufgabenteil c) folgt weiter:
aus Aufgabenteil c) folgt weiter:



 Somit stehen
Somit stehen  und
und  zueinander senkrecht.
zueinander senkrecht.
e)
Je weiter sich  dem Wert null annähert, desto mehr nähert sich die Tangente
dem Wert null annähert, desto mehr nähert sich die Tangente  der waagerechten Geraden mit der Gleichung
der waagerechten Geraden mit der Gleichung  an. Somit verschiebt sich ihr Schnittpunkt mit der
an. Somit verschiebt sich ihr Schnittpunkt mit der  -Achse immer weiter nach rechts auf der
-Achse immer weiter nach rechts auf der  -Achse. Somit gilt
-Achse. Somit gilt 
Je mehr sich dem Wert
dem Wert  annähert, desto mehr nähert sich
annähert, desto mehr nähert sich  der
der  -Achse an. In diesem Fall hätte das Dreieck keinen Flächeninhalt. Somit folgt
-Achse an. In diesem Fall hätte das Dreieck keinen Flächeninhalt. Somit folgt 
Je mehr sich
f)
Die Grundseite des Dreiecks liegt auf der  -Achse und wird durch den Koordinatenursprung sowie den Schnittpunkt von
-Achse und wird durch den Koordinatenursprung sowie den Schnittpunkt von  mit der
mit der  -Achse begrenzt. Die Länge der Grundseite entspricht daher der Nullstelle von
-Achse begrenzt. Die Länge der Grundseite entspricht daher der Nullstelle von  Die zugehörige Höhe ist die
Die zugehörige Höhe ist die  -Koordinate von
-Koordinate von  also
also  1. Schritt: Gleichung von
1. Schritt: Gleichung von  bestimmen
Nach Aufgabenteil c) ist die Steigung von
bestimmen
Nach Aufgabenteil c) ist die Steigung von  mit
mit  gegeben durch:
gegeben durch:
 Eine Punktprobe mit
Eine Punktprobe mit  liefert mit dem solve-Befehl des CAS:
liefert mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
t_k(x) &=& -\dfrac{k}{\sqrt{25-k^2}}\cdot x + b \\[5pt]
\sqrt{25-k^2} &=& -\dfrac{k}{\sqrt{25-k^2}}\cdot k + b \scriptsize \quad\mid \; CAS \\[5pt]
b &=& \dfrac{25}{\sqrt{25-k^2}}
\end{array}\)](https://www.schullv.de/api/node/mathjax-to-svg/809fc230edf2460cc6abc0350be926e49a124435faf5bede41d521cbadae2097?color=5a5a5a) Eine Gleichung von
Eine Gleichung von  ist also:
ist also:
 2. Schritt: Nullstelle von
2. Schritt: Nullstelle von  bestimmen
Mit dem solve-Befehl des CAS ergibt sich:
bestimmen
Mit dem solve-Befehl des CAS ergibt sich:
![\(\begin{array}[t]{rll}
t_k(x) &=& 0 \\[5pt]
-\dfrac{k}{\sqrt{25-k^2}}\cdot x + \dfrac{25}{\sqrt{25-k^2}} &=& 0 \quad \scriptsize \mid\; CAS \\[5pt]
x &=& \dfrac{25}{k}
\end{array}\)](https://www.schullv.de/api/node/mathjax-to-svg/4a3cf050ff835edb6ae81e62644099ea3fea203240d3b09cfbe1d44e24bef365?color=5a5a5a) Die Grundseite des Dreiecks besitzt daher die Länge
Die Grundseite des Dreiecks besitzt daher die Länge  3. Schritt: Term von
3. Schritt: Term von  nachweisen
Mit der Formel für den Flächeninhalt eines Dreiecks folgt:
nachweisen
Mit der Formel für den Flächeninhalt eines Dreiecks folgt:
![\(\begin{array}[t]{rll}
A(k) &=& \dfrac{1}{2}\cdot g_k \cdot h_k \\[5pt]
&=& \dfrac{1}{2}\cdot \frac{25}{k}\cdot \sqrt{25-k^2} \\[5pt]
&=& \dfrac{25}{2}\cdot\dfrac{\sqrt{25-k^2}}{k}\;[\text{FE}]
\end{array}\)](https://www.schullv.de/api/node/mathjax-to-svg/155fd6381a69ed4353737ce5e6c2b187f24ca618fadbefac915936b6bf774479?color=5a5a5a)
g)
Strenge Monotonie zeigen
Mit dem CAS ergibt sich:
 Wegen
Wegen  und
und  für
für ![\(k\in ]0;5[,\)](https://www.schullv.de/api/node/mathjax-to-svg/fe08cfb2d57aa3a1bb0aa55f759948b48afc3ec7d5e2a6ef364d7e70288bd6c3?color=5a5a5a) ist
ist  für alle
für alle ![\(k\in ]0;5[.\)](https://www.schullv.de/api/node/mathjax-to-svg/ee1f2136bf89edd15f43e4a4d2019be51ab08f49227cec1ca74423f6bfd9ec1e?color=5a5a5a)
Also nimmt in
in ![\(]0;5[\)](https://www.schullv.de/api/node/mathjax-to-svg/5eb96ef6f824de3ec8f723f9fbec9a15d67aa6c5c2fe306238b8649db51376d8?color=5a5a5a) streng monoton ab.
Wendestelle zeigen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
Mit Hilfe des solve-Befehls des CAS folgt für die Nullstellen von
streng monoton ab.
Wendestelle zeigen
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
Mit Hilfe des solve-Befehls des CAS folgt für die Nullstellen von 

 2. Schritt: Hinreichende Bedingung für Wendestellen überprüfen
Mit dem CAS ergibt sich:
2. Schritt: Hinreichende Bedingung für Wendestellen überprüfen
Mit dem CAS ergibt sich:
 Da
Da ![\(k_1\notin]0;5[,\)](https://www.schullv.de/api/node/mathjax-to-svg/d038327870d9494ebc353cc976e1e6ab4276e6074175b5897baa44284982e30b?color=5a5a5a) besitzt
besitzt  somit genau eine Wendestelle in diesem Intervall.
Bedeutung angeben
Die relative Abnahme des Flächeninhalts des Dreiecks ist für
somit genau eine Wendestelle in diesem Intervall.
Bedeutung angeben
Die relative Abnahme des Flächeninhalts des Dreiecks ist für  am größten, da
am größten, da 
Also nimmt
2
a)
Der Graph von  geht aus dem Graphen
geht aus dem Graphen  durch Stauchung mit dem Faktor
durch Stauchung mit dem Faktor  hervor, das heißt aus dem Halbkreis wird die Hälfte einer Ellipse.
Die Wertemenge von
hervor, das heißt aus dem Halbkreis wird die Hälfte einer Ellipse.
Die Wertemenge von  ist das Intervall
ist das Intervall ![\([0;5],\)](https://www.schullv.de/api/node/mathjax-to-svg/90109da518fdcc354a2d22cc5655dde53cedab8e61014541dafaeadc9ce39329?color=5a5a5a) somit ergibt sich die Wertemenge von
somit ergibt sich die Wertemenge von  als das Intervall
als das Intervall ![\(\left[0;\dfrac{b}{5}\cdot5\right] = [0;b].\)](https://www.schullv.de/api/node/mathjax-to-svg/ee9778adf7ca047f6b0aaa2e152cb571bbd0005275c5655e8abe86c46af03377?color=5a5a5a)
b)
c)
d)
Die durch die gestrichelte Linie dargestellte Ellipse entsteht aus  durch Spiegelung an der ersten Winkelhalbierenden. Somit handelt es sich hierbei um die Umkehrfunktion. Es folgt:
Ein Term einer Funktion, die im ersten Quadranten mit der gestrichelte Ellipse übereinstimmt, ist somit gegeben durch
durch Spiegelung an der ersten Winkelhalbierenden. Somit handelt es sich hierbei um die Umkehrfunktion. Es folgt:
Ein Term einer Funktion, die im ersten Quadranten mit der gestrichelte Ellipse übereinstimmt, ist somit gegeben durch 
e)
f)
1. Schritt: Flächeninhalt im zweiten Quadranten bestimmen
Die Nullstellen von  sind
sind  und
und  Der Inhalt der Fläche, die
Der Inhalt der Fläche, die  im zweiten Quadranten mit den Koordinatenachsen einschließt kann also durch folgendes Integral bestimmt werden:
im zweiten Quadranten mit den Koordinatenachsen einschließt kann also durch folgendes Integral bestimmt werden:
 2. Schritt:
2. Schritt:  bestimmen
bestimmen
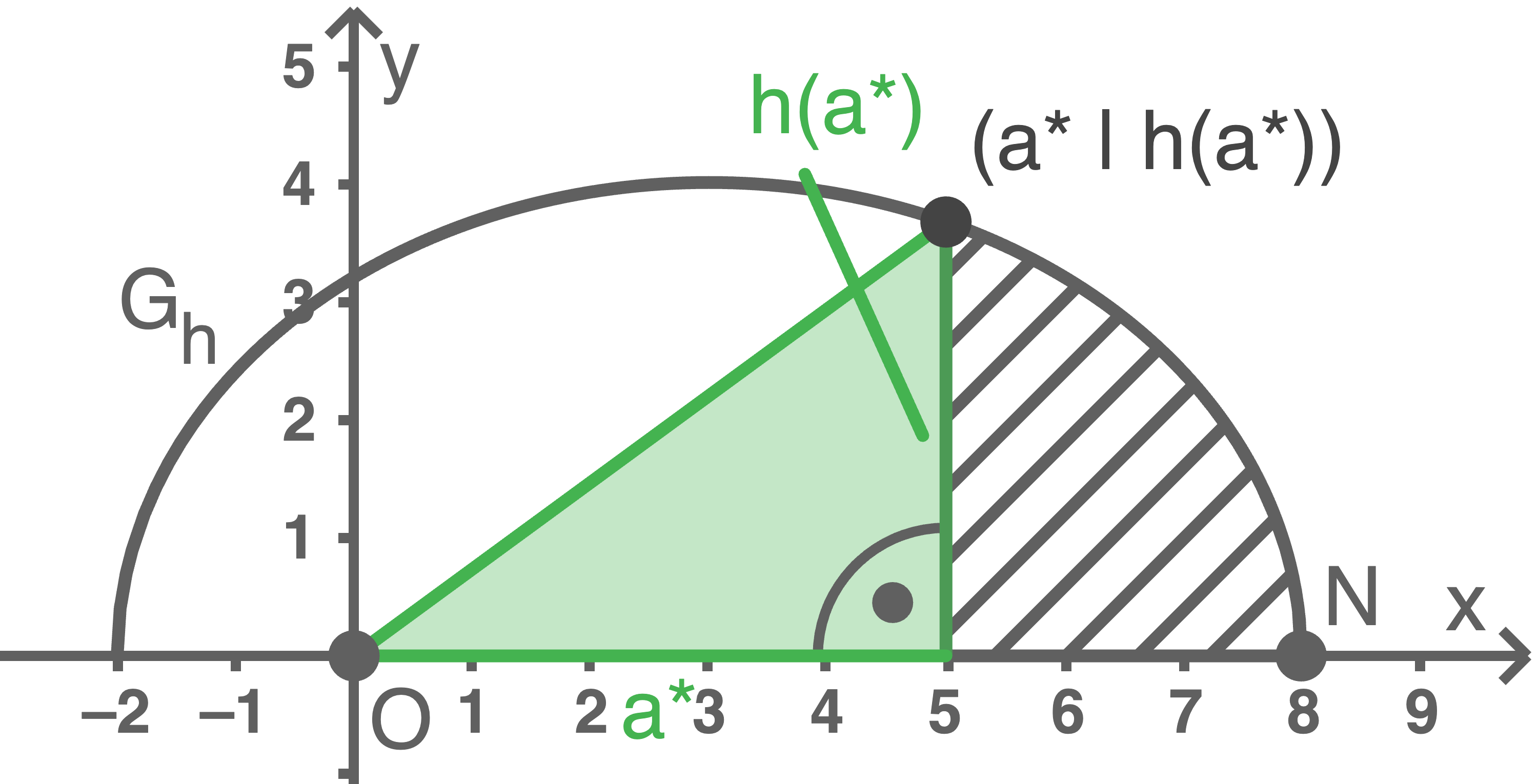 Das gesuchte Flächenstück setzt sich aus dem Integral über
Das gesuchte Flächenstück setzt sich aus dem Integral über  zwischen
zwischen  und
und  und einem Dreieck mit den Kathetenlängen
und einem Dreieck mit den Kathetenlängen  und
und  zusammen. Es gilt also:
zusammen. Es gilt also:
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:

g)
Punkt  einzeichnen
einzeichnen
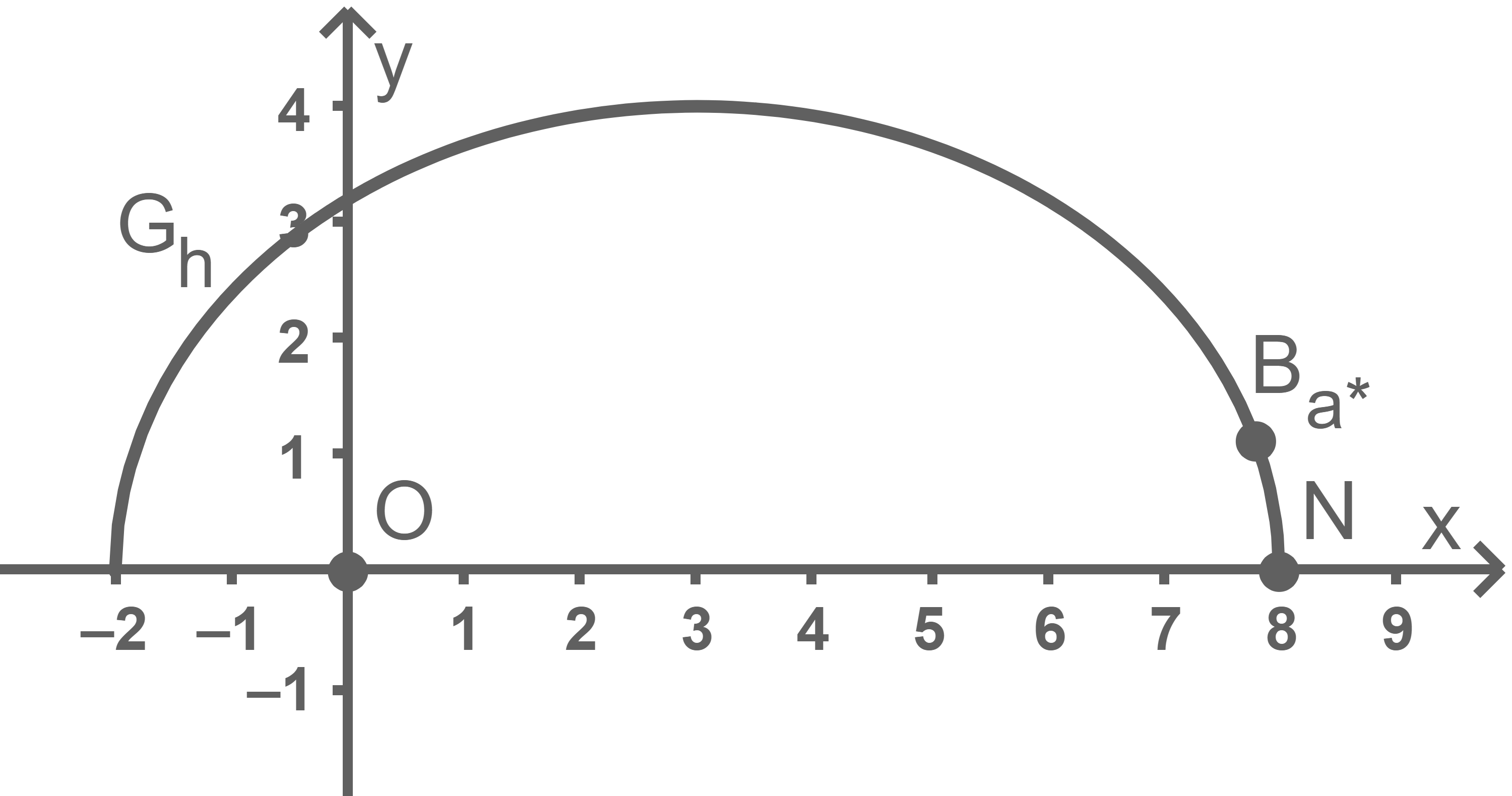 Mittlere Bahngeschwindigkeit begründen
Da der Planet laut Aufgabenstellung für die beiden beschriebenen Teilstücke der Bahn gleich viel Zeit benötigen muss, und in der Abbildung klar erkennbar ist, dass das Bahnstück im zweiten Quadranten länger ist als das andere, folgt, dass die mittlere Bahngeschwindigkeit im ersten Teilstück größer sein muss.
Mittlere Bahngeschwindigkeit begründen
Da der Planet laut Aufgabenstellung für die beiden beschriebenen Teilstücke der Bahn gleich viel Zeit benötigen muss, und in der Abbildung klar erkennbar ist, dass das Bahnstück im zweiten Quadranten länger ist als das andere, folgt, dass die mittlere Bahngeschwindigkeit im ersten Teilstück größer sein muss.

h)
Nach Aufgabenteil 2b) ist die Größe der durch die Planetenbahn eingeschlossenen Fläche 
![\(\approx 62,83\;[\text{FE}].\)](https://www.schullv.de/api/node/mathjax-to-svg/10c4d725f78b7017945815aca794eaa452f7cdae7a51ef82ba70939d1b6459a5?color=5a5a5a) Der Flächeninhalt des Teilstücks im zweiten Quadranten ergibt sich nach Aufgabenteil 2f) zu:
Der Flächeninhalt des Teilstücks im zweiten Quadranten ergibt sich nach Aufgabenteil 2f) zu:
 Der Planet braucht somit für einen vollständigen Umauf um den Stern ca.
Der Planet braucht somit für einen vollständigen Umauf um den Stern ca. 
