Stochastik Prüfungsteil B
Aufgabengruppe 1
Ein Getränkehersteller führt eine Werbeaktion durch, um die Verkaufszahlen seiner Saftschorlen zu erhöhen. Bei  der für die Werbeaktion produzierten zwei Millionen Flaschen wird auf der Innenseite des Verschlusses eine Marke für einen Geldgewinn angebracht. Von den Gewinnmarken sind
der für die Werbeaktion produzierten zwei Millionen Flaschen wird auf der Innenseite des Verschlusses eine Marke für einen Geldgewinn angebracht. Von den Gewinnmarken sind  jeweils
jeweils  wert, der Rest ist jeweils
wert, der Rest ist jeweils  wert. Alle Flaschen der Werbeaktion werden zufällig auf Kästen verteilt. Im Folgenden werden nur Flaschen aus der Werbeaktion betrachtet.
wert. Alle Flaschen der Werbeaktion werden zufällig auf Kästen verteilt. Im Folgenden werden nur Flaschen aus der Werbeaktion betrachtet.
1
Es wird eine Flasche geöffnet. Betrachtet werden folgende Ereignisse:
A: „Der Verschluss enthält eine Gewinnmarke.“
„Der Verschluss enthält eine Gewinnmarke.“
B: „Der Verschluss enthält eine Gewinnmarke im Wert von
„Der Verschluss enthält eine Gewinnmarke im Wert von  .“
.“
 und
und  .
.
Nachdem die zwei Millionen Flaschen verkauft sind, wird die Werbeaktion fortgesetzt. Der Getränkehersteller verspricht, dass weiterhin jede A:
B:
a)
Berechne die Wahrscheinlichkeiten  und
und  .
.
(2P)
b)
Es werden mehrere Flaschen geöffnet und für jede dieser Flaschen wird festgestellt, ob das Ereignis  eintritt. Begründe, dass dieses Zufallsexperiment näherungsweise durch eine Bernoullikette beschrieben werden kann.
eintritt. Begründe, dass dieses Zufallsexperiment näherungsweise durch eine Bernoullikette beschrieben werden kann.
Im Folgenden gilt beim Öffnen einer Flasche stets
(2P)
c)
Es werden nacheinander zehn Flaschen geöffnet. Berechne die Wahrscheinlichkeit dafür, dass sich erstmals in der letzten Flasche eine Gewinnmarke befindet und diese den Wert  hat.
hat.
(3P)
d)
Bestimme, z. B. durch systematisches Probieren, wie viele Flaschen man mindestens öffnen muss, um mit einer Wahrscheinlichkeit von mehr als  mindestens zwei Gewinnmarken zu finden.
mindestens zwei Gewinnmarken zu finden.
(4P)
e)
Berechne den Gesamtwert der Gewinnmarken, die Kunden beim Öffnen der  Flaschen eines Kastens im Mittel in den Verschlüssen finden.
Flaschen eines Kastens im Mittel in den Verschlüssen finden.
(3P)
2
Der Getränkehersteller bietet ihm an, anhand von  zufällig ausgewählten Flaschen einen Signifikanztest für die Nullhypothese „Die Wahrscheinlichkeit dafür, in einer Flasche eine Gewinnmarke zu finden, beträgt mindestens
zufällig ausgewählten Flaschen einen Signifikanztest für die Nullhypothese „Die Wahrscheinlichkeit dafür, in einer Flasche eine Gewinnmarke zu finden, beträgt mindestens  .“ auf einem Signifikanzniveau von
.“ auf einem Signifikanzniveau von  durchzuführen. Für den Fall, dass das Ergebnis des Tests im Ablehnungsbereich der Nullhypothese liegt, verspricht der Getränkehersteller, seine Abfüllanlage zu überprüfen und die Kosten für eine Sonderwerbeaktion des Getränkemarkts zu übernehmen.
Ermittle den Ablehnungsbereich der Nullhypothese und bestimme anschließend unter der Annahme, dass im Mittel nur
durchzuführen. Für den Fall, dass das Ergebnis des Tests im Ablehnungsbereich der Nullhypothese liegt, verspricht der Getränkehersteller, seine Abfüllanlage zu überprüfen und die Kosten für eine Sonderwerbeaktion des Getränkemarkts zu übernehmen.
Ermittle den Ablehnungsbereich der Nullhypothese und bestimme anschließend unter der Annahme, dass im Mittel nur  der Saftschorle-Flaschen eine Gewinnmarke enthalten, die Wahrscheinlichkeit dafür, dass der Getränkemarkt nicht in den Genuss einer kostenlosen Sonderwerbeaktion kommt.
der Saftschorle-Flaschen eine Gewinnmarke enthalten, die Wahrscheinlichkeit dafür, dass der Getränkemarkt nicht in den Genuss einer kostenlosen Sonderwerbeaktion kommt.
(6P)
(20P)
Aufgabengruppe 2
1
Nach einem Bericht zur Allergieforschung aus dem Jahr 2008 litt damals in Deutschland jeder vierte bis fünfte Einwohner an einer Allergie.  aller Allergiker reagierten allergisch auf Tierhaare. Kann aus diesen Aussagen gefolgert werden, dass 2008 mindestens
aller Allergiker reagierten allergisch auf Tierhaare. Kann aus diesen Aussagen gefolgert werden, dass 2008 mindestens  der Einwohner Deutschlands auf Tierhaare allergisch reagierten? Begründe deine Antwort.
der Einwohner Deutschlands auf Tierhaare allergisch reagierten? Begründe deine Antwort.
(3P)
2
Nach einer aktuellen Erhebung leiden  der Einwohner Deutschlands an einer Allergie. Aus den Einwohnern Deutschlands werden
der Einwohner Deutschlands an einer Allergie. Aus den Einwohnern Deutschlands werden  Personen zufällig ausgewählt.
Personen zufällig ausgewählt.
a)
Bestimme, wie groß  mindestens sein muss, damit mit einer Wahrscheinlichkeit von mehr als
mindestens sein muss, damit mit einer Wahrscheinlichkeit von mehr als  mindestens eine der ausgewählten Personen an einer Allergie leidet.
mindestens eine der ausgewählten Personen an einer Allergie leidet.
(3P)
b)
Ermittle, z. B. durch systematisches Probieren, wie groß  mindestens sein muss, damit die Wahrscheinlichkeit dafür, dass höchstens
mindestens sein muss, damit die Wahrscheinlichkeit dafür, dass höchstens  der ausgewählten Personen an einer Allergie leiden, kleiner als
der ausgewählten Personen an einer Allergie leiden, kleiner als  ist.
ist.
(3P)
c)
Im Folgenden ist  . Die Zufallsgröße
. Die Zufallsgröße  beschreibt die Anzahl der Personen unter den ausgewählten Personen, die an einer Allergie leiden. Bestimme die Wahrscheinlichkeit dafür, dass der Wert der binomialverteilten Zufallsgröße
beschreibt die Anzahl der Personen unter den ausgewählten Personen, die an einer Allergie leiden. Bestimme die Wahrscheinlichkeit dafür, dass der Wert der binomialverteilten Zufallsgröße  höchstens um eine Standardabweichung von ihrem Erwartungswert abweicht.
höchstens um eine Standardabweichung von ihrem Erwartungswert abweicht.
(4P)
3
Ein Pharmaunternehmen hat einen Hauttest zum Nachweis einer Tierhaarallergie entwickelt. Im Rahmen einer klinischen Studie zeigt sich, dass der Hauttest bei einer aus der Bevölkerung Deutschlands zufällig ausgewählten Person mit einer Wahrscheinlichkeit von  ein positives Testergebnis liefert. Leidet eine Person an einer Tierhaarallergie, so ist das Testergebnis mit einer Wahrscheinlichkeit von
ein positives Testergebnis liefert. Leidet eine Person an einer Tierhaarallergie, so ist das Testergebnis mit einer Wahrscheinlichkeit von  positiv. Das Testergebnis ist jedoch bei einer Person, die nicht an einer Tierhaarallergie leidet, mit einer Wahrscheinlichkeit von
positiv. Das Testergebnis ist jedoch bei einer Person, die nicht an einer Tierhaarallergie leidet, mit einer Wahrscheinlichkeit von  ebenfalls positiv.
ebenfalls positiv.
a)
Ermittle, welcher Anteil der Bevölkerung Deutschlands demnach allergisch auf Tierhaare reagiert.
(Ergebnis:  )
)
(3P)
b)
Eine aus der Bevölkerung Deutschlands zufällig ausgewählte Person wird getestet; das Testergebnis ist positiv. Berechne die Wahrscheinlichkeit dafür, dass diese Person tatsächlich an einer Tierhaarallergie leidet.
(2P)
c)
Aus der Bevölkerung Deutschlands wird eine Person zufällig ausgewählt und getestet. Beschreibe das Ereignis, dessen Wahrscheinlichkeit im Sachzusammenhang mit dem Term  berechnet wird.
berechnet wird.
(2P)
(20P)
Aufgabengruppe 1
 Wahrscheinlichkeiten berechnen
Von einem Getränkehersteller werden
Wahrscheinlichkeiten berechnen
Von einem Getränkehersteller werden  Flaschen für eine Werbeaktion produziert. Bei
Flaschen für eine Werbeaktion produziert. Bei  Flaschen wird eine Gewinnmarke in den Verschluss geklebt.
Flaschen wird eine Gewinnmarke in den Verschluss geklebt.  davon sind
davon sind  wert,
wert,  lediglich
lediglich  . Du sollst die Wahrscheinlichkeit zu zwei Ereignissen berechnen, wenn eine Flasche geöffnet wird:
. Du sollst die Wahrscheinlichkeit zu zwei Ereignissen berechnen, wenn eine Flasche geöffnet wird:
 berechnen
Die Wahrscheinlichkeit
berechnen
Die Wahrscheinlichkeit  erhältst du aus dem Quotienten der Flaschen mit Gewinnmarke und allen Flaschen.
erhältst du aus dem Quotienten der Flaschen mit Gewinnmarke und allen Flaschen.
![\(\begin{array}[t]{rll}
P(A)&=& \dfrac{100.000}{2.000.000} \\[5pt]
&=& 0,05 =5\%
\end{array}\)](https://mathjax.schullv.de/45a456b47b3062771ccc0ca9230a5ab3f2689b6699f4bb1aed618612aec9e076?color=5a5a5a) Die Wahrscheinlichkeit eine Flasche mit Gewinnmarke zu öffnen beträgt
Die Wahrscheinlichkeit eine Flasche mit Gewinnmarke zu öffnen beträgt  .
2. Schritt:
.
2. Schritt:  berechnen
Um auf die Wahrscheinlichkeit zu schließen eine Gewinnmarke im Wert von
berechnen
Um auf die Wahrscheinlichkeit zu schließen eine Gewinnmarke im Wert von  zu erhalten, verwendest du die Wahrscheinlichkeit für eine Gewinnmarke und berechnest mit dem Verhältnis der
zu erhalten, verwendest du die Wahrscheinlichkeit für eine Gewinnmarke und berechnest mit dem Verhältnis der  und
und  Marken die gesuchte Wahrscheinlichkeit.
Marken die gesuchte Wahrscheinlichkeit.
![\(\begin{array}[t]{rll}
P(B)&=& 0,05\cdot \dfrac{88.000}{100.000} \\[5pt]
&=& 0,044 =4,4\%
\end{array}\)](https://mathjax.schullv.de/f064c031dd635fb5ea13f25d6bf9aceca8525ffb04bdcfa8c2f51a4817a93bf9?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird eine Flasche mit einer
wird eine Flasche mit einer  Marke geöffnet.
Marke geöffnet.
 Zufallsexperiemnt als Bernoullikette begründen
Du sollst begründen, warum es sich bei dem Öffnen mehrerer Flaschen, näherungsweise um eine Bernoullikette handelt, wenn auf das Ereignis
Zufallsexperiemnt als Bernoullikette begründen
Du sollst begründen, warum es sich bei dem Öffnen mehrerer Flaschen, näherungsweise um eine Bernoullikette handelt, wenn auf das Ereignis  geprüft wird.
geprüft wird.
Eine Bernoullikette zeichnet aus, dass die Wahrscheinlichkeit in jedem Schritt gleich bleibt. Es werden mehrere, aber trotzdem wenige, Flaschen geöffnet. Da die Anzahl der Stichproben im Verhältniss zur Gesamtzahl klein ist, ändert sich die Wahrscheinlichkeit nicht wesentlich. Selbst wenn zehn Flaschen mit Gewinnmarke geöffnet werden, beträgt die Wahrscheinlichkeit gerundet weiterhin .
.
 Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass erstmals in der zehnten Flasche eine Gewinnmarke gefunden wird. Da du gerade festgestellt hast, dass sich dieses Experiment als Bernoullikette beschreiben lässt, ist die Zufallsvariable
Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass erstmals in der zehnten Flasche eine Gewinnmarke gefunden wird. Da du gerade festgestellt hast, dass sich dieses Experiment als Bernoullikette beschreiben lässt, ist die Zufallsvariable  , welche die Anzahl der Gewinnmarken angibt binomialverteilt mit
, welche die Anzahl der Gewinnmarken angibt binomialverteilt mit  . Um die Wahrscheinlichkeiten innerhalb einer Bernoullikette zu berechnen, verwendest du die Bernoulli-Formel:
In dieser Aufgabe kannst du den Binomialkoeffizienten
. Um die Wahrscheinlichkeiten innerhalb einer Bernoullikette zu berechnen, verwendest du die Bernoulli-Formel:
In dieser Aufgabe kannst du den Binomialkoeffizienten  jedoch vernachlässigen, da die Reihenfolge in welcher die Flaschen geöffnet werden, eine Rolle spielt. Du erhältst mit
jedoch vernachlässigen, da die Reihenfolge in welcher die Flaschen geöffnet werden, eine Rolle spielt. Du erhältst mit  geöffneten Flaschen und genau
geöffneten Flaschen und genau  Treffer:
Treffer:
![\(\begin{array}[t]{rll}
P(X=1)&=& 0,05^1 \cdot \left(1-0,05\right)^{10-1} \\[5pt]
&\approx& 0,0315 =3,15\%
\end{array}\)](https://mathjax.schullv.de/b6e4d433b86ba5352352eeacf05296347548431b7755ffdac793be57747c23f0?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  enthält erstmals die zehnte Flasche eine Gewinnmarke.
enthält erstmals die zehnte Flasche eine Gewinnmarke.
 Anzahl der Flaschen nachschlagen
Du sollst bestimmen, wie viele Flaschen geöffnet werden müssen, also wie groß
Anzahl der Flaschen nachschlagen
Du sollst bestimmen, wie viele Flaschen geöffnet werden müssen, also wie groß  sein muss, um mit einer Wahrscheinlichkeit von mindestens
sein muss, um mit einer Wahrscheinlichkeit von mindestens  , mindestens zwei Gewinnmarken zu erhalten. Du betrachtest also die Ungleichung in
, mindestens zwei Gewinnmarken zu erhalten. Du betrachtest also die Ungleichung in  :
:
![\(\begin{array}[t]{rll}
P(X\geq 2)&=& \sum\limits_{k=2}^n \binom{n}{k}\cdot 0,05^k\cdot 0,95^{n-k} \\[5pt]
0,05 &\leq& \sum\limits_{k=2}^n \binom{n}{k}\cdot 0,05^k\cdot 0,95^{n-k}
\end{array}\)](https://mathjax.schullv.de/532a3b401bc0a2fd7f80d91e2a2dfa096753c1c2ac5d7964a6a1f09b664d5ef1?color=5a5a5a) Um diese Ungleichung mit dem nspire zu lösen verwendest du eine Tabelle und den Befehl „binomialCDf“. Du findest ihn unter:
Um diese Ungleichung mit dem nspire zu lösen verwendest du eine Tabelle und den Befehl „binomialCDf“. Du findest ihn unter:
 aufsteigend. Für „Binom Cdf“ benutzt in der ersten Zeile der ersten Spalte die Untergrenze
aufsteigend. Für „Binom Cdf“ benutzt in der ersten Zeile der ersten Spalte die Untergrenze  , die Obergrenze
, die Obergrenze  , die Anzahl der Versuche
, die Anzahl der Versuche  und die Wahrscheinlichkeit
und die Wahrscheinlichkeit  . Das Feld ziehst du nach unten, um den Befehl zu vervielfachen.
. Das Feld ziehst du nach unten, um den Befehl zu vervielfachen.
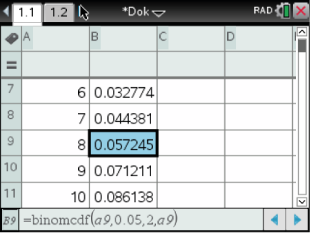 Abb. 1: Binomialverteilung mit dem nspire lösen
Du erkennst, dass
Abb. 1: Binomialverteilung mit dem nspire lösen
Du erkennst, dass  gelten muss, da dort die Wahrscheinlichkeit erstmals größer als
gelten muss, da dort die Wahrscheinlichkeit erstmals größer als  ist.
ist.
 Gesamtwert der Gewinnmarken berechnen
Du sollst den Gesamtwert der Gewinnmarken berechnen, die ein Kunde erhält, wenn er zwanzig Flaschen öffnet. Dazu berechnest du den Erwartungswert
Gesamtwert der Gewinnmarken berechnen
Du sollst den Gesamtwert der Gewinnmarken berechnen, die ein Kunde erhält, wenn er zwanzig Flaschen öffnet. Dazu berechnest du den Erwartungswert  einer geöffneten Flasche. Diesen erhältst du aus der Multiplikation des Ergebnisses mit der zugehörigen Wahrscheinlichkeit.
Ein Kunde kann bei einer Flasche mit einem Gewinn von
einer geöffneten Flasche. Diesen erhältst du aus der Multiplikation des Ergebnisses mit der zugehörigen Wahrscheinlichkeit.
Ein Kunde kann bei einer Flasche mit einem Gewinn von  rechnen. Bei zwanzig Flaschen sind also
rechnen. Bei zwanzig Flaschen sind also  .
.
 Hypothesentest durchführen
Nach dem die ersten zwei Millionen Flaschen verkauft wurden, gibt der Herstellen bekannt, dass die Aktion verlängert wurde. Du sollst überprüfen ob die Wahrscheinlichkeit für einen Gewinn bei
Hypothesentest durchführen
Nach dem die ersten zwei Millionen Flaschen verkauft wurden, gibt der Herstellen bekannt, dass die Aktion verlängert wurde. Du sollst überprüfen ob die Wahrscheinlichkeit für einen Gewinn bei  geblieben ist . Dazu stellst du eine Nullhypothese und eine Alternativhypothese auf.
geblieben ist . Dazu stellst du eine Nullhypothese und eine Alternativhypothese auf.
 :
: 
 :
:  Du betrachtest die Ungleichung in
Du betrachtest die Ungleichung in  bei einem Signifikanzniveau, welche als Grenzwahrscheinlichkeit dient, von
bei einem Signifikanzniveau, welche als Grenzwahrscheinlichkeit dient, von  und
und  getesteten Flaschen:
Mit dem Taschenrechner löst du diese Aufgabe wie zuvor 1)
getesteten Flaschen:
Mit dem Taschenrechner löst du diese Aufgabe wie zuvor 1) d). Du benutzt, in der ersten Zeile,
d). Du benutzt, in der ersten Zeile,  als Untergrenze,
als Untergrenze,  als Obergrenze,
als Obergrenze,  als Anzahl der Versuche und
als Anzahl der Versuche und  als Wahrscheinlichkeit.
als Wahrscheinlichkeit.
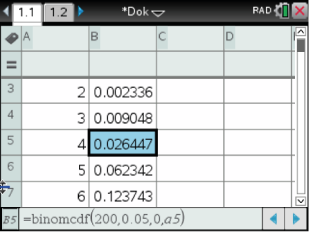 Abb. 2: Binomialverteilung mit dem nspire lösen
Für
Abb. 2: Binomialverteilung mit dem nspire lösen
Für  beträgt die Wahrscheinlichkeit das Erste mal mehr als
beträgt die Wahrscheinlichkeit das Erste mal mehr als  . Der Ablehnungsbereich der Nullhypothese ist
. Der Ablehnungsbereich der Nullhypothese ist  . Werden weniger als vier Flaschen mit einer Gewinnmarke gefunden, ist davon auszugehen, dass die Wahrscheinlichkeit kleiner als
. Werden weniger als vier Flaschen mit einer Gewinnmarke gefunden, ist davon auszugehen, dass die Wahrscheinlichkeit kleiner als  ist und die Nullhypothese ist abzulehnen.
ist und die Nullhypothese ist abzulehnen.
 Fehler 2. Art berechnen
Du sollst bestimmen mit welcher Wahrscheinlichkeit der Getränkehersteller keine Sonderwerbeveranstaltung bezahlt, obwohl die Wahrscheinlichkeit für eine Gewinnmarke nur
Fehler 2. Art berechnen
Du sollst bestimmen mit welcher Wahrscheinlichkeit der Getränkehersteller keine Sonderwerbeveranstaltung bezahlt, obwohl die Wahrscheinlichkeit für eine Gewinnmarke nur  beträgt. Gesucht ist der Fehler 2. Art. Den Fehler 2. Art
beträgt. Gesucht ist der Fehler 2. Art. Den Fehler 2. Art  bestimmst du mit
bestimmst du mit  , wobei du nun die Wahrscheinlichkeit
, wobei du nun die Wahrscheinlichkeit  benutzt und
benutzt und  durch den Annahmebereich der Nullhypothese festgelegt wird auf
durch den Annahmebereich der Nullhypothese festgelegt wird auf  .
.
![\(\begin{array}[t]{rll}
\beta&=& 1-\sum\limits_{k=0}^3\binom{200}{k}\cdot 0,03^k\cdot 0,97^{200-k} \\[5pt]
&\approx& 0,8528 =85,28\%
\end{array}\)](https://mathjax.schullv.de/46f68e99b6265dd11e8708e5a208e5a70e131303387a7888ed200f7e06fcba49?color=5a5a5a) Erneut löst du diese Aufgabe mit dem Befehl ‚Binom Cdf‘, allerdings kannst du nun direkt das „Berechnen“ Fenster verwenden. Du verwendest
Erneut löst du diese Aufgabe mit dem Befehl ‚Binom Cdf‘, allerdings kannst du nun direkt das „Berechnen“ Fenster verwenden. Du verwendest  für die Untergrenze,
für die Untergrenze,  für die Obergrenze,
für die Obergrenze,  für die Anzahl der Versuche und
für die Anzahl der Versuche und  als Wahrscheinlichkeit.
als Wahrscheinlichkeit.
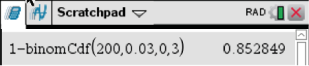 Abb. 3: Binomialverteilung mit dem nspire lösen
Es liegt mit
Abb. 3: Binomialverteilung mit dem nspire lösen
Es liegt mit  ein Fehler 2. Art vor.
Aufgabengruppe 2
ein Fehler 2. Art vor.
Aufgabengruppe 2
 Aussage begründen
Du sollst begründen, ob es möglich ist zu behaupten, dass mindestens
Aussage begründen
Du sollst begründen, ob es möglich ist zu behaupten, dass mindestens  aller Einwohner an einer Tierhaarallergie litten. Hier wurde eine „mindetens“ Aussage getroffen, das heißt es ist das Minimum zu bestimmen. Die Wahrscheinlichkeit, dass eine Person Allergiker ist, beträgt also
aller Einwohner an einer Tierhaarallergie litten. Hier wurde eine „mindetens“ Aussage getroffen, das heißt es ist das Minimum zu bestimmen. Die Wahrscheinlichkeit, dass eine Person Allergiker ist, beträgt also  und nicht
und nicht  . Betrachtest du weiter die Allergiker mit Tierhaarallergie beträgt die Wahrscheinlichkeit dafür
. Betrachtest du weiter die Allergiker mit Tierhaarallergie beträgt die Wahrscheinlichkeit dafür  . Für eine Tierhaarallergie ergibt sich:
. Für eine Tierhaarallergie ergibt sich:
![\(\begin{array}[t]{rll}
P(T)&=& P(A)\cdot P(T\vert A) \\[5pt]
&=& 0,082 =8,2\%
\end{array}\)](https://mathjax.schullv.de/6070b9eb46246e9fb30fafb48874fb4b2fb843cd1e9728f444a3cdd025eaa712?color=5a5a5a)
 sind weniger als
sind weniger als  . Somit kann man nicht bestätigen, dass jeder zehnte Einwohner an einer Tierhaarallergie litt.
. Somit kann man nicht bestätigen, dass jeder zehnte Einwohner an einer Tierhaarallergie litt.
 Notwendige Anzahl bestimmen
Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als
Notwendige Anzahl bestimmen
Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als  , mindestens eine der Personen an einer Allergie leidet. Da die Anzahl der Einwohner Deutschlands wesentlich größer ist, als die Anzahl der befragten Personen kannst du davon ausgehen, dass die Zufallsvariable
, mindestens eine der Personen an einer Allergie leidet. Da die Anzahl der Einwohner Deutschlands wesentlich größer ist, als die Anzahl der befragten Personen kannst du davon ausgehen, dass die Zufallsvariable  mit
mit  binomialverteilt ist. Für binomialverteilte Zufallsvariablen kannst du die Bernoulli-Formel benutzen, welche mit
binomialverteilt ist. Für binomialverteilte Zufallsvariablen kannst du die Bernoulli-Formel benutzen, welche mit  der Anzahl der untersuchten Personen,
der Anzahl der untersuchten Personen,  der Anzahl der Allergiker und
der Anzahl der Allergiker und  die Wahrscheinlichkeit für
die Wahrscheinlichkeit für  aus
aus  allergischen Personen angibt.
Da mindestens eine Person an einer Allergie leiden soll, erhältst du eine Ungleichung in
allergischen Personen angibt.
Da mindestens eine Person an einer Allergie leiden soll, erhältst du eine Ungleichung in  , wobei du um die Rechnung zu vereinfach, das Gegenereignis betrachtest:
, wobei du um die Rechnung zu vereinfach, das Gegenereignis betrachtest:
![\(\begin{array}[t]{rll}
P(X\geq 1)&=& 1-P(X=0) \\[5pt]
1-0,99&\geq& \binom{n}{0}\cdot 0,25^0\cdot 0,75^{n} \\[5pt]
0,01&\geq& 0,75^n
\end{array}\)](https://mathjax.schullv.de/14d5300b69c6bb59e334d7a2075b307f0ca66e6f33c7d0a206e52f7705ca017f?color=5a5a5a) Diese Gleichung kannst du von deinem Taschenrechner lösen lassen. Den Befehl findest du unter:
Diese Gleichung kannst du von deinem Taschenrechner lösen lassen. Den Befehl findest du unter:
 Abb. 4: Gleichung lösen mit dem nspire
Da ein ganzahliges Ergebnis anzugeben ist, müssen mindestens 17 Personen untersucht werden.
Abb. 4: Gleichung lösen mit dem nspire
Da ein ganzahliges Ergebnis anzugeben ist, müssen mindestens 17 Personen untersucht werden.
 Minimale Anzahl bestimmen Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, sodass die Wahrscheinlichkeit, dass höchstens
Minimale Anzahl bestimmen Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, sodass die Wahrscheinlichkeit, dass höchstens  davon an einer Allergie leiden, kleiner als
davon an einer Allergie leiden, kleiner als  ist. Du benutzt erneut die Tabellenfunktion des Taschenrechners und den Befehl „Binom Cdf“. Dabei benutzt du, in der ersten Zeile,
ist. Du benutzt erneut die Tabellenfunktion des Taschenrechners und den Befehl „Binom Cdf“. Dabei benutzt du, in der ersten Zeile,  als Untergrenze,
als Untergrenze,  als Obergrenze,
als Obergrenze,  als Anzahl der Versuche und
als Anzahl der Versuche und  als Wahrscheinlichkeit.
als Wahrscheinlichkeit.
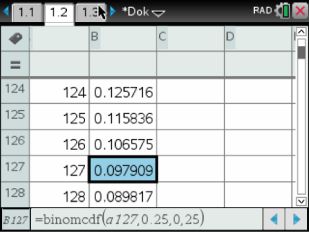 Abb. 5: Binomialverteilung mit dem nspire lösen
Für
Abb. 5: Binomialverteilung mit dem nspire lösen
Für  ist die Wahrscheinlichkeit erstmals kleiner als
ist die Wahrscheinlichkeit erstmals kleiner als  . Es müssen also mindestens
. Es müssen also mindestens  Personen ausgewählt werden.
Personen ausgewählt werden.
 Wahrscheinlichkeit für Abweichung vom Erwartungswert bestimmen
Es werden
Wahrscheinlichkeit für Abweichung vom Erwartungswert bestimmen
Es werden  Personen untersucht und du sollst bestimmen mit welcher Wahrscheinlichkeit ein das Ergebnis im
Personen untersucht und du sollst bestimmen mit welcher Wahrscheinlichkeit ein das Ergebnis im  Intervall liegt. Zum lösen benötigst du den Erwartungswert
Intervall liegt. Zum lösen benötigst du den Erwartungswert  und die Standardabweichung
und die Standardabweichung  . Für Binomialverteilungen gilt:
. Für Binomialverteilungen gilt:
![\(\begin{array}[t]{rll}
\mu &=& n\cdot p \\[5pt]
&=& 200\cdot 0,25 \\[5pt]
&=& 50
\end{array}\)](https://mathjax.schullv.de/f8ecf724a86e8ee69c0b3d18635580c3a35aa163d040f1d207f7bff5ca5ac708?color=5a5a5a)
![\(\begin{array}[t]{rll}
\sigma &=& \sqrt{n\cdot p\cdot (1-p)} \\[5pt]
&=& \sqrt{200\cdot 0,25\cdot 0,75} \\[5pt]
&\approx& 6,12
\end{array}\)](https://mathjax.schullv.de/6f31877755328e9972bdb6738b1df8f3ab5904e38e22b2e07248ac49805d331d?color=5a5a5a) Das
Das  Intervall ist dementsprechend
Intervall ist dementsprechend ![\(\left[\lceil\mu-\sigma\rceil,\lfloor\mu+\sigma\rfloor\right]=\left[44,56\right]\)](https://mathjax.schullv.de/60299bc7884f5c8ef945bf3b530415920fd8ea9ee63ee3282825b5744b55fd6f?color=5a5a5a) . Die Wahrscheinlichkeit, dass die Anzahl der Allergiker in diesem Intervall liegt, berechnest du mit dem Befehl „binomialCDf“. Du verwendest
. Die Wahrscheinlichkeit, dass die Anzahl der Allergiker in diesem Intervall liegt, berechnest du mit dem Befehl „binomialCDf“. Du verwendest  als Untergrenze,
als Untergrenze,  als Obergrenze,
als Obergrenze,  und
und  .
.
 Abb. : Binomialverteilung mit dem nspire lösen
Mit einer Wahrscheinlichkeit von
Abb. : Binomialverteilung mit dem nspire lösen
Mit einer Wahrscheinlichkeit von  liegt die Anzahl der Allergiker im
liegt die Anzahl der Allergiker im  Intervall und weicht somit maximal um eine Standardabweichung vom Erwartungswert ab.
Intervall und weicht somit maximal um eine Standardabweichung vom Erwartungswert ab.
 Wahrscheinlichkeit für Tierhaarallergie berechnen
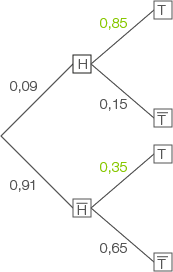
Du sollst berechnen mit welcher Wahrscheinlichkeit eine zufällig ausgewählte Testperson an einer Tierhaarallergie leidet. Dazu betrachtest du die zwei Ereignisse und trägst sie in einem Baumdiagramm auf:
Somit kannst du
Wahrscheinlichkeit für Tierhaarallergie berechnen
Du sollst berechnen mit welcher Wahrscheinlichkeit eine zufällig ausgewählte Testperson an einer Tierhaarallergie leidet. Dazu betrachtest du die zwei Ereignisse und trägst sie in einem Baumdiagramm auf:
Somit kannst du  berechnen mit:
berechnen mit:
 der Bevölkerung reagiert allergisch auf Tierhaare.
der Bevölkerung reagiert allergisch auf Tierhaare.
 Wahrscheinlichkeit für korrektes Testergebnis berechnen
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein positives Testergebnis korrekt ist. Gesucht ist also die Wahrscheinlichkeit für eine Tierhaarallergie unter der Bedingung, dass der Test positiv ausfällt. Dazu kannst du den Satz von Bayes verwenden:
Wahrscheinlichkeit für korrektes Testergebnis berechnen
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein positives Testergebnis korrekt ist. Gesucht ist also die Wahrscheinlichkeit für eine Tierhaarallergie unter der Bedingung, dass der Test positiv ausfällt. Dazu kannst du den Satz von Bayes verwenden:
 Die Wahrscheinlichkeit
Die Wahrscheinlichkeit  hast du oben bereits berechnet. Die Wahrscheinlichkeit für einen positiven Test insgesamt kennst du aus der Aufgabenstellung
hast du oben bereits berechnet. Die Wahrscheinlichkeit für einen positiven Test insgesamt kennst du aus der Aufgabenstellung  .
.  ist die Wahrscheinlichkeit für einen positiven Test, falls der getestet Patient eine Tierhaarallergie hat und kann ebenfalls aus der Aufgabenstellung abgelesen werden.
Somit kannst du, unter Verwendung der Bayschen Formel, die gesuchte Wahrscheinlichkeit berechnen:
ist die Wahrscheinlichkeit für einen positiven Test, falls der getestet Patient eine Tierhaarallergie hat und kann ebenfalls aus der Aufgabenstellung abgelesen werden.
Somit kannst du, unter Verwendung der Bayschen Formel, die gesuchte Wahrscheinlichkeit berechnen:
![\(\begin{array}[t]{rll}
P(H\vert T)&=& \dfrac{P(T\vert H)\cdot P(H)}{P(T)} \\[5pt]
&=&\dfrac{0,85\cdot 0,09}{0,395} \\[5pt]
&\approx& 0,1937=19,37\%
\end{array}\)](https://mathjax.schullv.de/51fedd2b3b724b7e5f67362a78323770cc3f7e66fe93ea9c50b42d11bbae54ae?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  ist eine positiv getestete Person wirklich allergisch.
ist eine positiv getestete Person wirklich allergisch.
 Term im Sachzusammenhang interpretieren
Du sollst den Term
Term im Sachzusammenhang interpretieren
Du sollst den Term  im Sachzusammenhang interpretieren. Du erkennst, dass es sich durch die Addition um zwei verschieden Ereignisse handelt. Betrachte beide Teile getrennt.
1. Teil:
im Sachzusammenhang interpretieren. Du erkennst, dass es sich durch die Addition um zwei verschieden Ereignisse handelt. Betrachte beide Teile getrennt.
1. Teil:  Die Wahrscheinlichkeit
Die Wahrscheinlichkeit  zeigt an, dass eine Person an einer Tierhaarallergie leidet.
zeigt an, dass eine Person an einer Tierhaarallergie leidet.  ist die Wahrscheinlichkeit, dass der Test trotzdem negativ ist.
2. Teil:
ist die Wahrscheinlichkeit, dass der Test trotzdem negativ ist.
2. Teil: 
 ist die Wahrscheinlichkeit, dass eine Person nicht an einer Tierhaarallergie leidet.
ist die Wahrscheinlichkeit, dass eine Person nicht an einer Tierhaarallergie leidet.  zeigt an, dass der Test trotzdem positiv ist.
Zusammenfassend ergibt sich, dass der Term die Wahrscheinlichkeit angibt, dass der Test nicht funktioniert.
zeigt an, dass der Test trotzdem positiv ist.
Zusammenfassend ergibt sich, dass der Term die Wahrscheinlichkeit angibt, dass der Test nicht funktioniert.
1)
a)
: Der Verschluss enthält eine Gewinnmarke
: Der Verschluss enthält eine Gewinnmarke im Wert von
b)
Eine Bernoullikette zeichnet aus, dass die Wahrscheinlichkeit in jedem Schritt gleich bleibt. Es werden mehrere, aber trotzdem wenige, Flaschen geöffnet. Da die Anzahl der Stichproben im Verhältniss zur Gesamtzahl klein ist, ändert sich die Wahrscheinlichkeit nicht wesentlich. Selbst wenn zehn Flaschen mit Gewinnmarke geöffnet werden, beträgt die Wahrscheinlichkeit gerundet weiterhin
c)
d)
Menü  Statistik
Statistik  Verteilung
Verteilung  Binom Cdf
Binom Cdf
Du befüllst die Spalte A mit den Zahlen  Abb. 1: Binomialverteilung mit dem nspire lösen
Abb. 1: Binomialverteilung mit dem nspire lösen
e)
2)
 Abb. 2: Binomialverteilung mit dem nspire lösen
Abb. 2: Binomialverteilung mit dem nspire lösen
 Abb. 3: Binomialverteilung mit dem nspire lösen
Abb. 3: Binomialverteilung mit dem nspire lösen
1)
2)
a)
Menü  Algebra
Algebra  Löse
Löse
 Abb. 4: Gleichung lösen mit dem nspire
Abb. 4: Gleichung lösen mit dem nspire
b)
 Abb. 5: Binomialverteilung mit dem nspire lösen
Abb. 5: Binomialverteilung mit dem nspire lösen
c)
 Abb. : Binomialverteilung mit dem nspire lösen
Abb. : Binomialverteilung mit dem nspire lösen
3)
a)
: Test ist positiv
: Person reagiert auf Tierhaare allergisch
b)
c)
Aufgabengruppe 1
 Wahrscheinlichkeiten berechnen
Von einem Getränkehersteller werden
Wahrscheinlichkeiten berechnen
Von einem Getränkehersteller werden  Flaschen für eine Werbeaktion produziert. Bei
Flaschen für eine Werbeaktion produziert. Bei  Flaschen wird eine Gewinnmarke in den Verschluss geklebt.
Flaschen wird eine Gewinnmarke in den Verschluss geklebt.  davon sind
davon sind  wert,
wert,  lediglich
lediglich  . Du sollst die Wahrscheinlichkeit zu zwei Ereignissen berechnen, wenn eine Flasche geöffnet wird:
. Du sollst die Wahrscheinlichkeit zu zwei Ereignissen berechnen, wenn eine Flasche geöffnet wird:
 berechnen
Die Wahrscheinlichkeit
berechnen
Die Wahrscheinlichkeit  erhältst du aus dem Quotienten der Flaschen mit Gewinnmarke und allen Flaschen.
erhältst du aus dem Quotienten der Flaschen mit Gewinnmarke und allen Flaschen.
![\(\begin{array}[t]{rll}
P(A)&=& \dfrac{100.000}{2.000.000} \\[5pt]
&=& 0,05 =5\%
\end{array}\)](https://mathjax.schullv.de/9df3522671d08a537bbc6f1b4f675a457581770d23ee8eb0da2f62f3512b53ca?color=5a5a5a) Die Wahrscheinlichkeit eine Flasche mit Gewinnmarke zu öffnen beträgt
Die Wahrscheinlichkeit eine Flasche mit Gewinnmarke zu öffnen beträgt  .
2. Schritt:
.
2. Schritt:  berechnen
Um auf die Wahrscheinlichkeit zu schließen eine Gewinnmarke im Wert von
berechnen
Um auf die Wahrscheinlichkeit zu schließen eine Gewinnmarke im Wert von  zu erhalten, verwendest du die Wahrscheinlichkeit für eine Gewinnmarke und berechnest mit dem Verhältnis der
zu erhalten, verwendest du die Wahrscheinlichkeit für eine Gewinnmarke und berechnest mit dem Verhältnis der  und
und  Marken die gesuchte Wahrscheinlichkeit.
Marken die gesuchte Wahrscheinlichkeit.
![\(\begin{array}[t]{rll}
P(B)&=& 0,05\cdot \dfrac{88.000}{100.000} \\[5pt]
&=& 0,044 =4,4\%
\end{array}\)](https://mathjax.schullv.de/f064c031dd635fb5ea13f25d6bf9aceca8525ffb04bdcfa8c2f51a4817a93bf9?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird eine Flasche mit einer
wird eine Flasche mit einer  Marke geöffnet.
Marke geöffnet.
 Zufallsexperiemnt als Bernoullikette begründen
Du sollst begründen, warum es sich bei dem Öffnen mehrerer Flaschen, näherungsweise um eine Bernoullikette handelt, wenn auf das Ereignis
Zufallsexperiemnt als Bernoullikette begründen
Du sollst begründen, warum es sich bei dem Öffnen mehrerer Flaschen, näherungsweise um eine Bernoullikette handelt, wenn auf das Ereignis  geprüft wird.
geprüft wird.
Eine Bernoullikette zeichnet aus, dass die Wahrscheinlichkeit in jedem Schritt gleich bleibt. Es werden mehrere, aber trotzdem wenige, Flaschen geöffnet. Da die Anzahl der Stichproben im Verhältniss zur Gesamtzahl klein ist, ändert sich die Wahrscheinlichkeit nicht wesentlich. Selbst wenn zehn Flaschen mit Gewinnmarke geöffnet werden, beträgt die Wahrscheinlichkeit gerundet weiterhin .
.
 Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass erstmals in der zehnten Flasche eine Gewinnmarke gefunden wird. Da du gerade festgestellt hast, dass sich dieses Experiment als Bernoullikette beschreiben lässt, ist die Zufallsvariable
Wahrscheinlichkeit berechnen
Du sollst die Wahrscheinlichkeit berechnen, dass erstmals in der zehnten Flasche eine Gewinnmarke gefunden wird. Da du gerade festgestellt hast, dass sich dieses Experiment als Bernoullikette beschreiben lässt, ist die Zufallsvariable  , welche die Anzahl der Gewinnmarken angibt binomialverteilt mit
, welche die Anzahl der Gewinnmarken angibt binomialverteilt mit  . Um die Wahrscheinlichkeiten innerhalb einer Bernoullikette zu berechnen, verwendest du die Bernoulli-Formel:
In dieser Aufgabe kannst du den Binomialkoeffizienten
. Um die Wahrscheinlichkeiten innerhalb einer Bernoullikette zu berechnen, verwendest du die Bernoulli-Formel:
In dieser Aufgabe kannst du den Binomialkoeffizienten  jedoch vernachlässigen, da die Reihenfolge in welcher die Flaschen geöffnet werden, eine Rolle spielt. Du erhältst mit
jedoch vernachlässigen, da die Reihenfolge in welcher die Flaschen geöffnet werden, eine Rolle spielt. Du erhältst mit  geöffneten Flaschen und genau
geöffneten Flaschen und genau  Treffer:
Treffer:
![\(\begin{array}[t]{rll}
P(X=1)&=& 0,05^1 \cdot \left(1-0,05\right)^{10-1} \\[5pt]
&\approx& 0,0315 =3,15\%
\end{array}\)](https://mathjax.schullv.de/b6e4d433b86ba5352352eeacf05296347548431b7755ffdac793be57747c23f0?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  enthält erstmals die zehnte Flasche eine Gewinnmarke.
enthält erstmals die zehnte Flasche eine Gewinnmarke.
 Anzahl der Flaschen nachschlagen
Du sollst bestimmen, wie viele Flaschen geöffnet werden müssen, also wie groß
Anzahl der Flaschen nachschlagen
Du sollst bestimmen, wie viele Flaschen geöffnet werden müssen, also wie groß  sein muss, um mit einer Wahrscheinlichkeit von mindestens
sein muss, um mit einer Wahrscheinlichkeit von mindestens  , mindestens zwei Gewinnmarken zu erhalten. Du betrachtest also die Ungleichung in
, mindestens zwei Gewinnmarken zu erhalten. Du betrachtest also die Ungleichung in  :
:
![\(\begin{array}[t]{rll}
P(X\geq 2)&=& \sum\limits_{k=2}^n \binom{n}{k}\cdot 0,05^k\cdot 0,95^{n-k} \\[5pt]
0,05 &\leq& \sum\limits_{k=2}^n \binom{n}{k}\cdot 0,05^k\cdot 0,95^{n-k}
\end{array}\)](https://mathjax.schullv.de/532a3b401bc0a2fd7f80d91e2a2dfa096753c1c2ac5d7964a6a1f09b664d5ef1?color=5a5a5a) Um diese Ungleichung mit dem Classpad zu lösen verwendest du eine Tabelle und den Befehl „binomialCDf“. Du findest ihn unter:
Um diese Ungleichung mit dem Classpad zu lösen verwendest du eine Tabelle und den Befehl „binomialCDf“. Du findest ihn unter:
 , die Obergrenze
, die Obergrenze  , die Anzahl der Versuche
, die Anzahl der Versuche  und die Wahrscheinlichkeit
und die Wahrscheinlichkeit  . Kopiere dies in das Graphikfenster und lasse ihn in einer Tabelle ausrechnen.
. Kopiere dies in das Graphikfenster und lasse ihn in einer Tabelle ausrechnen.
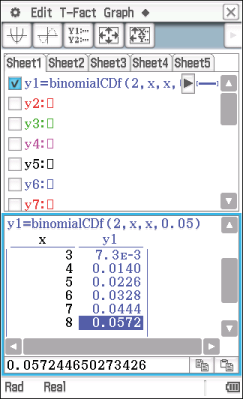 Abb. 1: Binomialverteilung mit dem Classpad lösen
Du erkennst, dass
Abb. 1: Binomialverteilung mit dem Classpad lösen
Du erkennst, dass  gelten muss, da dort die Wahrscheinlichkeit erstmals größer als
gelten muss, da dort die Wahrscheinlichkeit erstmals größer als  ist.
ist.
 Gesamtwert der Gewinnmarken berechnen
Du sollst den Gesamtwert der Gewinnmarken berechnen, die ein Kunde erhält, wenn er zwanzig Flaschen öffnet. Dazu berechnest du den Erwartungswert
Gesamtwert der Gewinnmarken berechnen
Du sollst den Gesamtwert der Gewinnmarken berechnen, die ein Kunde erhält, wenn er zwanzig Flaschen öffnet. Dazu berechnest du den Erwartungswert  einer geöffneten Flasche. Diesen erhältst du aus der Multiplikation des Ergebnisses mit der zugehörigen Wahrscheinlichkeit.
Ein Kunde kann bei einer Flasche mit einem Gewinn von
einer geöffneten Flasche. Diesen erhältst du aus der Multiplikation des Ergebnisses mit der zugehörigen Wahrscheinlichkeit.
Ein Kunde kann bei einer Flasche mit einem Gewinn von  rechnen. Bei zwanzig Flaschen sind also
rechnen. Bei zwanzig Flaschen sind also  .
.
 Hypothesentest durchführen
Nach dem die ersten zwei Millionen Flaschen verkauft wurden, gibt der Herstellen bekannt, dass die Aktion verlängert wurde. Du sollst überprüfen ob die Wahrscheinlichkeit für einen Gewinn bei
Hypothesentest durchführen
Nach dem die ersten zwei Millionen Flaschen verkauft wurden, gibt der Herstellen bekannt, dass die Aktion verlängert wurde. Du sollst überprüfen ob die Wahrscheinlichkeit für einen Gewinn bei  geblieben ist . Dazu stellst du eine Nullhypothese und eine Alternativhypothese auf.
geblieben ist . Dazu stellst du eine Nullhypothese und eine Alternativhypothese auf.
 :
: 
 :
:  Du betrachtest die Ungleichung in
Du betrachtest die Ungleichung in  bei einem Signifikanzniveau, welche als Grenzwahrscheinlichkeit dient, von
bei einem Signifikanzniveau, welche als Grenzwahrscheinlichkeit dient, von  und
und  getesteten Flaschen:
Mit dem Taschenrechner löst du diese Aufgabe wie zuvor 1)
getesteten Flaschen:
Mit dem Taschenrechner löst du diese Aufgabe wie zuvor 1) d). Du benutzt
d). Du benutzt  als Untergrenze,
als Untergrenze,  als Obergrenze,
als Obergrenze,  als Anzahl der Versuche und
als Anzahl der Versuche und  als Wahrscheinlichkeit.
als Wahrscheinlichkeit.
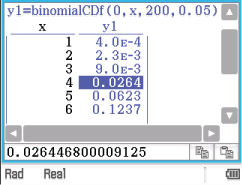 Abb. 2: Binomialverteilung mit dem Classpad lösen
Für
Abb. 2: Binomialverteilung mit dem Classpad lösen
Für  beträgt die Wahrscheinlichkeit das Erste mal mehr als
beträgt die Wahrscheinlichkeit das Erste mal mehr als  . Der Ablehnungsbereich der Nullhypothese ist
. Der Ablehnungsbereich der Nullhypothese ist  . Werden weniger als vier Flaschen mit einer Gewinnmarke gefunden, ist davon auszugehen, dass die Wahrscheinlichkeit kleiner als
. Werden weniger als vier Flaschen mit einer Gewinnmarke gefunden, ist davon auszugehen, dass die Wahrscheinlichkeit kleiner als  ist und die Nullhypothese ist abzulehnen.
ist und die Nullhypothese ist abzulehnen.
 Fehler 2. Art berechnen
Du sollst bestimmen mit welcher Wahrscheinlichkeit der Getränkehersteller keine Sonderwerbeveranstaltung bezahlt, obwohl die Wahrscheinlichkeit für eine Gewinnmarke nur
Fehler 2. Art berechnen
Du sollst bestimmen mit welcher Wahrscheinlichkeit der Getränkehersteller keine Sonderwerbeveranstaltung bezahlt, obwohl die Wahrscheinlichkeit für eine Gewinnmarke nur  beträgt. Gesucht ist der Fehler 2. Art. Den Fehler 2. Art
beträgt. Gesucht ist der Fehler 2. Art. Den Fehler 2. Art  bestimmst du mit
bestimmst du mit  , wobei du nun die Wahrscheinlichkeit
, wobei du nun die Wahrscheinlichkeit  benutzt und
benutzt und  durch den Annahmebereich der Nullhypothese festgelegt wird auf
durch den Annahmebereich der Nullhypothese festgelegt wird auf  .
.
![\(\begin{array}[t]{rll}
\beta&=& 1-\sum\limits_{k=0}^3\binom{200}{k}\cdot 0,03^k\cdot 0,97^{200-k} \\[5pt]
&\approx& 0,8528 =85,28\%
\end{array}\)](https://mathjax.schullv.de/46f68e99b6265dd11e8708e5a208e5a70e131303387a7888ed200f7e06fcba49?color=5a5a5a) Erneut löst du diese Aufgabe mit dem Befehl ‚binomialCDf‘, allerdings kannst du nun direkt das „Main“ Fenster verwenden. Du verwendest
Erneut löst du diese Aufgabe mit dem Befehl ‚binomialCDf‘, allerdings kannst du nun direkt das „Main“ Fenster verwenden. Du verwendest  für die Untergrenze,
für die Untergrenze,  für die Obergrenze,
für die Obergrenze,  für die Anzahl der Versuche und
für die Anzahl der Versuche und  als Wahrscheinlichkeit.
als Wahrscheinlichkeit.
 Abb. 3: Binomialverteilung mit dem Classpad lösen
Es liegt mit
Abb. 3: Binomialverteilung mit dem Classpad lösen
Es liegt mit  ein Fehler 2. Art vor.
Aufgabengruppe 2
ein Fehler 2. Art vor.
Aufgabengruppe 2
 Aussage begründen
Du sollst begründen, ob es möglich ist zu behaupten, dass mindestens
Aussage begründen
Du sollst begründen, ob es möglich ist zu behaupten, dass mindestens  aller Einwohner an einer Tierhaarallergie litten. Hier wurde eine „mindetens“ Aussage getroffen, das heißt es ist das Minimum zu bestimmen. Die Wahrscheinlichkeit, dass eine Person Allergiker ist, beträgt also
aller Einwohner an einer Tierhaarallergie litten. Hier wurde eine „mindetens“ Aussage getroffen, das heißt es ist das Minimum zu bestimmen. Die Wahrscheinlichkeit, dass eine Person Allergiker ist, beträgt also  und nicht
und nicht  . Betrachtest du weiter die Allergiker mit Tierhaarallergie beträgt die Wahrscheinlichkeit dafür
. Betrachtest du weiter die Allergiker mit Tierhaarallergie beträgt die Wahrscheinlichkeit dafür  . Für eine Tierhaarallergie ergibt sich:
. Für eine Tierhaarallergie ergibt sich:
![\(\begin{array}[t]{rll}
P(T)&=& P(A)\cdot P(T\vert A) \\[5pt]
&=& 0,082 =8,2\%
\end{array}\)](https://mathjax.schullv.de/6070b9eb46246e9fb30fafb48874fb4b2fb843cd1e9728f444a3cdd025eaa712?color=5a5a5a)
 sind weniger als
sind weniger als  . Somit kann man nicht bestätigen, dass jeder zehnte Einwohner an einer Tierhaarallergie litt.
. Somit kann man nicht bestätigen, dass jeder zehnte Einwohner an einer Tierhaarallergie litt.
 Notwendige Anzahl bestimmen
Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als
Notwendige Anzahl bestimmen
Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als  , mindestens eine der Personen an einer Allergie leidet. Da die Anzahl der Einwohner Deutschlands wesentlich größer ist, als die Anzahl der befragten Personen kannst du davon ausgehen, dass die Zufallsvariable
, mindestens eine der Personen an einer Allergie leidet. Da die Anzahl der Einwohner Deutschlands wesentlich größer ist, als die Anzahl der befragten Personen kannst du davon ausgehen, dass die Zufallsvariable  mit
mit  binomialverteilt ist. Für binomialverteilte Zufallsvariablen kannst du die Bernoulli-Formel benutzen, welche mit
binomialverteilt ist. Für binomialverteilte Zufallsvariablen kannst du die Bernoulli-Formel benutzen, welche mit  der Anzahl der untersuchten Personen,
der Anzahl der untersuchten Personen,  der Anzahl der Allergiker und
der Anzahl der Allergiker und  die Wahrscheinlichkeit für
die Wahrscheinlichkeit für  aus
aus  allergischen Personen angibt.
Da mindestens eine Person an einer Allergie leiden soll, erhältst du eine Ungleichung in
allergischen Personen angibt.
Da mindestens eine Person an einer Allergie leiden soll, erhältst du eine Ungleichung in  , wobei du um die Rechnung zu vereinfach, das Gegenereignis betrachtest:
, wobei du um die Rechnung zu vereinfach, das Gegenereignis betrachtest:
![\(\begin{array}[t]{rll}
P(X\geq 1)&=& 1-P(X=0) \\[5pt]
1-0,99&\geq& \binom{n}{0}\cdot 0,25^0\cdot 0,75^{n} \\[5pt]
0,01&\geq& 0,75^n
\end{array}\)](https://mathjax.schullv.de/89e8182c6ff504f326056dae8f586814ad9c9e8afe0523befd791ece92131ec6?color=5a5a5a) Diese Gleichung kannst du von deinem Taschenrechner lösen lassen. Den Befehl findest du unter:
Diese Gleichung kannst du von deinem Taschenrechner lösen lassen. Den Befehl findest du unter:
 Abb. 4: Gleichung lösen mit dem Classpad
Da ein ganzahliges Ergebnis anzugeben ist, müssen mindestens 17 Personen untersucht werden.
Abb. 4: Gleichung lösen mit dem Classpad
Da ein ganzahliges Ergebnis anzugeben ist, müssen mindestens 17 Personen untersucht werden.
 Minimale Anzahl bestimmen Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, sodass die Wahrscheinlichkeit, dass höchstens
Minimale Anzahl bestimmen Du sollst bestimmen, wie viele Personen ausgewählt werden müssen, sodass die Wahrscheinlichkeit, dass höchstens  davon an einer Allergie leiden, kleiner als
davon an einer Allergie leiden, kleiner als  ist. Du benutzt erneut die Tabellenfunktion des Taschenrechners und den Befehl „binomialCDf“. Dabei benutzt du
ist. Du benutzt erneut die Tabellenfunktion des Taschenrechners und den Befehl „binomialCDf“. Dabei benutzt du  als Untergrenze,
als Untergrenze,  als Obergrenze,
als Obergrenze,  als Anzahl der Versuche und
als Anzahl der Versuche und  als Wahrscheinlichkeit.
als Wahrscheinlichkeit.
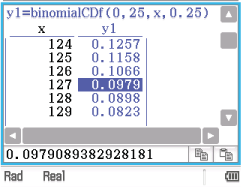 Abb. 5: Binomialverteilung mit dem Classpad lösen
Für
Abb. 5: Binomialverteilung mit dem Classpad lösen
Für  ist die Wahrscheinlichkeit erstmals kleiner als
ist die Wahrscheinlichkeit erstmals kleiner als  . Es müssen also mindestens
. Es müssen also mindestens  Personen ausgewählt werden.
Personen ausgewählt werden.
 Wahrscheinlichkeit für Abweichung vom Erwartungswert bestimmen
Es werden
Wahrscheinlichkeit für Abweichung vom Erwartungswert bestimmen
Es werden  Personen untersucht und du sollst bestimmen mit welcher Wahrscheinlichkeit ein das Ergebnis im
Personen untersucht und du sollst bestimmen mit welcher Wahrscheinlichkeit ein das Ergebnis im  Intervall liegt. Zum lösen benötigst du den Erwartungswert
Intervall liegt. Zum lösen benötigst du den Erwartungswert  und die Standardabweichung
und die Standardabweichung  . Für Binomialverteilungen gilt:
. Für Binomialverteilungen gilt:
![\(\begin{array}[t]{rll}
\mu &=& n\cdot p \\[5pt]
&=& 200\cdot 0,25 \\[5pt]
&=& 50
\end{array}\)](https://mathjax.schullv.de/f8ecf724a86e8ee69c0b3d18635580c3a35aa163d040f1d207f7bff5ca5ac708?color=5a5a5a)
![\(\begin{array}[t]{rll}
\sigma &=& \sqrt{n\cdot p\cdot (1-p)} \\[5pt]
&=& \sqrt{200\cdot 0,25\cdot 0,75} \\[5pt]
&\approx& 6,12
\end{array}\)](https://mathjax.schullv.de/6f31877755328e9972bdb6738b1df8f3ab5904e38e22b2e07248ac49805d331d?color=5a5a5a) Das
Das  Intervall ist dementsprechend
Intervall ist dementsprechend ![\(\left[\lceil\mu-\sigma\rceil,\lfloor\mu+\sigma\rfloor\right]=\left[44,56\right]\)](https://mathjax.schullv.de/60299bc7884f5c8ef945bf3b530415920fd8ea9ee63ee3282825b5744b55fd6f?color=5a5a5a) . Die Wahrscheinlichkeit, dass die Anzahl der Allergiker in diesem Intervall liegt, berechnest du mit dem Befehl „binomialCDf“. Du verwendest
. Die Wahrscheinlichkeit, dass die Anzahl der Allergiker in diesem Intervall liegt, berechnest du mit dem Befehl „binomialCDf“. Du verwendest  als Untergrenze,
als Untergrenze,  als Obergrenze,
als Obergrenze,  und
und  .
.
 Abb. : Binomialverteilung mit dem Classpad lösen
Mit einer Wahrscheinlichkeit von
Abb. : Binomialverteilung mit dem Classpad lösen
Mit einer Wahrscheinlichkeit von  liegt die Anzahl der Allergiker im
liegt die Anzahl der Allergiker im  Intervall und weicht somit maximal um eine Standardabweichung vom Erwartungswert ab.
Intervall und weicht somit maximal um eine Standardabweichung vom Erwartungswert ab.
 Wahrscheinlichkeit für Tierhaarallergie berechnen
Du sollst berechnen mit welcher Wahrscheinlichkeit eine zufällig ausgewählte Testperson an einer Tierhaarallergie leidet. Dazu betrachtest du die zwei Ereignisse und trägst sie in einem Baumdiagramm am. Die aus der Aufgabe bekannten Wahrscheinlichkeiten sind grün markiert:
Somit kannst du
Wahrscheinlichkeit für Tierhaarallergie berechnen
Du sollst berechnen mit welcher Wahrscheinlichkeit eine zufällig ausgewählte Testperson an einer Tierhaarallergie leidet. Dazu betrachtest du die zwei Ereignisse und trägst sie in einem Baumdiagramm am. Die aus der Aufgabe bekannten Wahrscheinlichkeiten sind grün markiert:
Somit kannst du  berechnen mit:
berechnen mit:
 der Bevölkerung reagiert allergisch auf Tierhaare.
der Bevölkerung reagiert allergisch auf Tierhaare.
 Wahrscheinlichkeit für korrektes Testergebnis berechnen
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein positives Testergebnis korrekt ist. Gesucht ist also die Wahrscheinlichkeit für eine Tierhaarallergie unter der Bedingung, dass der Test positiv ausfällt. Dazu kannst du den Satz von Bayes verwenden:
Wahrscheinlichkeit für korrektes Testergebnis berechnen
Du sollst berechnen, mit welcher Wahrscheinlichkeit ein positives Testergebnis korrekt ist. Gesucht ist also die Wahrscheinlichkeit für eine Tierhaarallergie unter der Bedingung, dass der Test positiv ausfällt. Dazu kannst du den Satz von Bayes verwenden:
 Die Wahrscheinlichkeit
Die Wahrscheinlichkeit  hast du oben bereits berechnet. Die Wahrscheinlichkeit für einen positiven Test insgesamt kennst du aus der Aufgabenstellung
hast du oben bereits berechnet. Die Wahrscheinlichkeit für einen positiven Test insgesamt kennst du aus der Aufgabenstellung  .
.  ist die Wahrscheinlichkeit für einen positiven Test, falls der getestet Patient eine Tierhaarallergie hat und kann ebenfalls aus der Aufgabenstellung abgelesen werden.
Somit kannst du, unter Verwendung der Bayschen Formel, die gesuchte Wahrscheinlichkeit berechnen:
ist die Wahrscheinlichkeit für einen positiven Test, falls der getestet Patient eine Tierhaarallergie hat und kann ebenfalls aus der Aufgabenstellung abgelesen werden.
Somit kannst du, unter Verwendung der Bayschen Formel, die gesuchte Wahrscheinlichkeit berechnen:
![\(\begin{array}[t]{rll}
P(H\vert T)&=& \dfrac{P(T\vert H)\cdot P(H)}{P(T)} \\[5pt]
&=&\dfrac{0,85\cdot 0,09}{0,395} \\[5pt]
&\approx& 0,1937=19,37\%
\end{array}\)](https://mathjax.schullv.de/51fedd2b3b724b7e5f67362a78323770cc3f7e66fe93ea9c50b42d11bbae54ae?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  ist eine positiv getestete Person wirklich allergisch.
ist eine positiv getestete Person wirklich allergisch.
 Term im Sachzusammenhang interpretieren
Du sollst den Term
Term im Sachzusammenhang interpretieren
Du sollst den Term  im Sachzusammenhang interpretieren. Du erkennst, dass es sich durch die Addition um zwei verschieden Ereignisse handelt. Betrachte beide Teile getrennt.
1. Teil:
im Sachzusammenhang interpretieren. Du erkennst, dass es sich durch die Addition um zwei verschieden Ereignisse handelt. Betrachte beide Teile getrennt.
1. Teil:  Die Wahrscheinlichkeit
Die Wahrscheinlichkeit  zeigt an, dass eine Person an einer Tierhaarallergie leidet.
zeigt an, dass eine Person an einer Tierhaarallergie leidet.  ist die Wahrscheinlichkeit, dass der Test trotzdem negativ ist.
2. Teil:
ist die Wahrscheinlichkeit, dass der Test trotzdem negativ ist.
2. Teil: 
 ist die Wahrscheinlichkeit, dass eine Person nicht an einer Tierhaarallergie leidet.
ist die Wahrscheinlichkeit, dass eine Person nicht an einer Tierhaarallergie leidet.  zeigt an, dass der Test trotzdem positiv ist.
Zusammenfassend ergibt sich, dass der Term die Wahrscheinlichkeit angibt, dass der Test nicht funktioniert.
zeigt an, dass der Test trotzdem positiv ist.
Zusammenfassend ergibt sich, dass der Term die Wahrscheinlichkeit angibt, dass der Test nicht funktioniert.
1)
a)
: Der Verschluss enthält eine Gewinnmarke
: Der Verschluss enthält eine Gewinnmarke im Wert von
b)
Eine Bernoullikette zeichnet aus, dass die Wahrscheinlichkeit in jedem Schritt gleich bleibt. Es werden mehrere, aber trotzdem wenige, Flaschen geöffnet. Da die Anzahl der Stichproben im Verhältniss zur Gesamtzahl klein ist, ändert sich die Wahrscheinlichkeit nicht wesentlich. Selbst wenn zehn Flaschen mit Gewinnmarke geöffnet werden, beträgt die Wahrscheinlichkeit gerundet weiterhin
c)
d)
Interactive  Distribution/Inv.Dist.
Distribution/Inv.Dist.  Discrete
Discrete  binomialCDf
binomialCDf
In diesem Befehl benutzt du die Untergrenze  Abb. 1: Binomialverteilung mit dem Classpad lösen
Abb. 1: Binomialverteilung mit dem Classpad lösen
e)
2)
 Abb. 2: Binomialverteilung mit dem Classpad lösen
Abb. 2: Binomialverteilung mit dem Classpad lösen
 Abb. 3: Binomialverteilung mit dem Classpad lösen
Abb. 3: Binomialverteilung mit dem Classpad lösen
1)
2)
a)
Interactive  Advanced
Advanced  solve
solve
 Abb. 4: Gleichung lösen mit dem Classpad
Abb. 4: Gleichung lösen mit dem Classpad
b)
 Abb. 5: Binomialverteilung mit dem Classpad lösen
Abb. 5: Binomialverteilung mit dem Classpad lösen
c)
 Abb. : Binomialverteilung mit dem Classpad lösen
Abb. : Binomialverteilung mit dem Classpad lösen
3)
a)
: Test ist positiv
: Person reagiert auf Tierhaare allergisch
b)
c)