Teil B

Der in der Abbildung 1 dargestellte Körper wird begrenzt von der quadratischen Grundfläche $ABCD$ mit $A( 5|5|0),$ $B(-5|5|0),$ $C (-5| -5|0)$ und $D(5|-5|0),$ acht dreieckigen Seitenflächen und einem weiteren Quadrat $EFGH$ mit $E (2|0|4),$ $F (0|2|4),$ $G(-2|0|4)$ und $H (0|-2|4).$
Der Mittelpunkt $S$ des Quadrats $ABCD$ ist der Ursprung des Koordinatensystems und der gesamte Körper ist symmetrisch sowohl bezüglich der $x_1x_3$ -Ebene als auch bezüglich der $x_2x_3$ -Ebene.

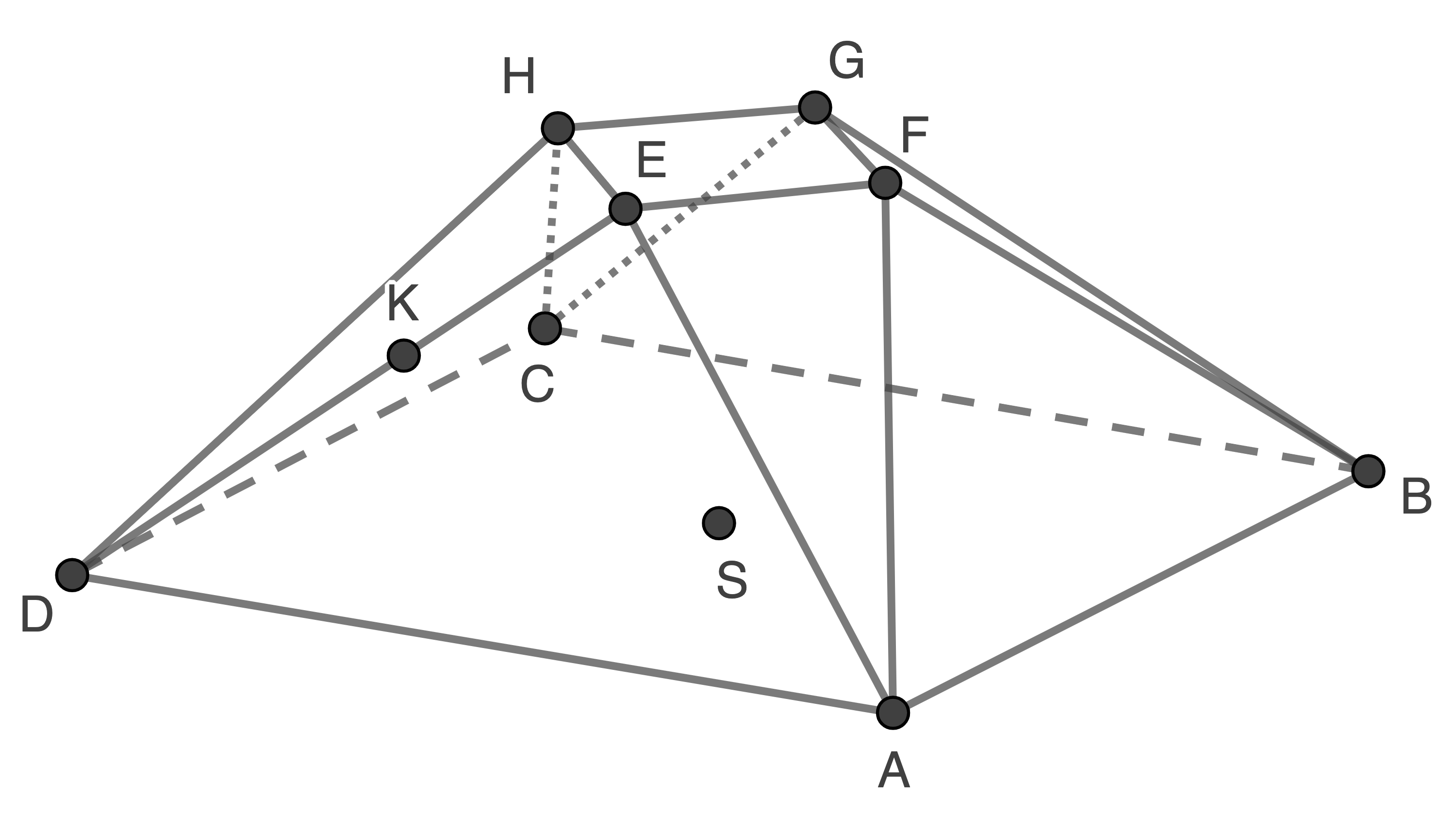
Diagramm mit Punkten und Linien, das eine geometrische Struktur darstellt.

Abb. 1

Zeige, dass das Dreieck $ABF$ bei $F$ rechtwinklig ist.

(2 BE)

Das Dreieck $ABF$ liegt in der Ebene $W$ . Ermittle eine Gleichung von $W$ in Koordinatenform und beschreibe die besondere Lage von $W$ im Koordinatensystem.

[zur Kontrolle: $W: 4x_2 +3x_3 -20 =0$ ]

(3 BE)

Berechne die Größe des spitzen Winkels, den die Seitenfläche $ABF$ und die Grundfläche $ABCD$ einschließen.

(3 BE)

Auf der Strecke $[DE]$ gibt es einen Punkt $K,$ für den $\overline{KE}= \overline{EF}$ gilt.

Bestimme die Koordinaten von $K$ .

[zur Kontrolle: $K(3,2|-2|2,4)$ ]

(4 BE)

Der Mittelpunkt der Strecke $[KF]$ wird mit $N$ bezeichnet. Begründe, dass die Gerade $EN$ die Winkelhalbierende des Dreiecks $DFE$ bei $E$ ist, und weise rechnerisch nach, dass $S$ auf der Gerade $EN$ liegt.

(5 BE)

Der Körper kann in neun Pyramiden zerlegt werden, von denen jede kongruent zu genau einer der drei Pyramiden $ABFS,$ $HDES$ bzw. $EFGHS$ ist (vgl. Abbildung 2). Die Pyramide $ABFS$ hat das Volumen $33 \dfrac{1}{3}.$ Bestimme das Volumen des gesamten Körpers.

Diagramm mit geometrischen Formen, Punkten und Linien, das eine komplexe Struktur darstellt.

Grafische Darstellung eines geometrischen Modells mit mehreren Punkten und Linien.

Abb. 2

(5 BE)

Es gibt genau eine Kugel, auf der alle acht Eckpunkte des Körpers liegen. Ermittle die Koordinaten des Mittelpunkts dieser Kugel.

(3 BE)

(25 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\overrightarrow{FA}= \pmatrix{5\\5\\0}-\pmatrix{0\\2\\4}=\pmatrix{5\\3\\-4}$

$\overrightarrow{FB}= \pmatrix{-5\\5\\0}-\pmatrix{0\\2\\4}=\pmatrix{-5\\3\\-4}$

Berechnung des Skalarproduktes anzeigen

$\overrightarrow{FA} \circ \overrightarrow{FB} =0$

Da das Skalarprodukt von $\overrightarrow{FA}$ und $\overrightarrow{FB}$ Null ergibt, besitzt das Dreieck $ABF$ bei $F$ einen rechten Winkel.

Ebenengleichung von W
Mit dem Kreuzprodukt und dem crossP-Befehl des CAS kann ein Normalenvektor von $W$ bestimmt werden:

Vollständige Rechnung anzeigen

$\overrightarrow{n_W} = 10\cdot \pmatrix{0\\4\\3}$

Die Koordinatengleichung ergibt sich wie folgt.

$\begin{array}[t]{rlll} 4x_2+3x_3 +c &=& 0 \quad \scriptsize \mid\;\text{A einsetzen} \\[5pt] 4\cdot 5+3\cdot 0 +c &=& 0 \quad \scriptsize \mid\; -20 \\[5pt] c &=& -20 \\[5pt] \end{array}$

$W: 4x_2+3x_3-20=0$

Besondere Lage von W
Die $x_1$ -Koordinate des Normalenvektors $\overrightarrow{n_W}$ ist Null, deshalb ist die Ebene $W$ parallel zur $x_1-$ Achse.

Die Größe des Winkels, den die Seitenfläche $ABF$ und die Grundfläche $ABCD$ einschließt, kann mit $\overrightarrow{n_W}$ der Ebene $W$ und einem Normalenvektor der $x_1x_2$ -Ebene berechnet werden.

Rechenweg anzeigen

\cos(\alpha) = \frac{3}{5}

Der Winkel ist folglich $\alpha=\cos^{-1} \left(\dfrac{3}{5} \right) \approx 53,1^{\circ}$ groß.

Um den Vektor $\overrightarrow{EK}$ zu erhalten, wird $\overrightarrow{ED}$ normiert und mit der Länge von $\overrightarrow{EF}$ multiplizier. Damit folgt:

Vollständigen Rechenweg anzeigen

$\overrightarrow{OK} = \pmatrix{3,2\\-2\\2,4}$

Die Koordinaten lauten $K(3,2 \mid -2 \mid 2,4).$

Begründung
Da $\overline{EK} = \overline{EF}$ gilt, ist das Dreieck $KFE$ gleichschenklig. Da $N$ der Mittelpunkt der Strecke $[KF]$ ist, halbiert die Gerade $EN$ also den Innenwinkel des Dreiecks $KFE$ bei $E.$
Da $K$ auf $[ED]$ liegt, entspricht der Innenwinkel des Dreiecks $KFE$ bei $E$ dem Innenwinkel des Dreiecks $DFE$ bei $E.$ Dieser wird somit ebenfalls von der Geraden $EN$ halbiert.

Nachweis
$\overrightarrow{ON} = \overrightarrow{OK}+ \frac{1}{2}\cdot \overrightarrow{KF}$ $= \pmatrix{3,2\\ -2 \\ 2,4} + \frac{1}{2}\cdot \pmatrix{-3,2\\4\\1,6} = \pmatrix{1,6 \\ 0 \\ 3,2}$

$\overrightarrow{EN}= \pmatrix{1,6-2\\0-0\\3,2-4} = \pmatrix{-0,4\\0\\-0,8}$

Die Gerade $EN$ kann also durch folgende Gleichung beschrieben werden:

$EN:\, \overrightarrow{x}= \pmatrix{2\\0\\4} + \lambda \cdot\pmatrix{-0,4\\0\\-0,8},$ $\lambda\in \mathbb{R}$

Aus der Punktprobe mit $S$ folgt:

$\pmatrix{0\\0\\0}= \pmatrix{2\\0\\4} + \lambda \cdot\pmatrix{-0,4\\0\\-0,8}$

$\pmatrix{-2\\0\\-4}= \lambda \cdot\pmatrix{-0,4\\0\\-0,8}$

$\pmatrix{5\\0\\5}= \pmatrix{\lambda\\0\\\lambda}$

Folglich liegt $S$ auf der Geraden $EN.$

Der Körper besteht aus 4 $ABFS$ Pyramiden, 4 $HDES$ Pyramiden und einer $EFGHS$ Pyramide. Es muss nun jeweils das Volumen der Pyramiden $EFGHS$ und $HDES$ berechnet werden.

Die allgemeine Formel zur Volumenberechnung einer Pyramide lautet $V_P=\dfrac{1}{3} \cdot G\cdot h.$

Die Höhe der $EFGHS$ Pyramide ergibt sich aus der $x_3$ -Koordinate von $E,$ $F,$ $G$ und $H$ und beträgt demnach $h=4.$ Damit folgt:

$V_{EFGHS}=\frac{1}{3} \cdot \left| \overrightarrow{EF}\right|^2 \cdot h$ $= \frac{1}{3} \cdot \sqrt{8}^2 \cdot 4 = \frac{32}{3}$

Das Volumen der Pyramide $HDES$ kann mit dem Spatprodukt berechnet werden:

$V_{HDES} = \frac{1}{6}\cdot \left| \overrightarrow{SH}\circ \left(\overrightarrow{SD}\times \overrightarrow{SE} \right)\right|$ $= \frac{40}{3}$

Für das Volumen des Körpers gilt:

$V= 4 \cdot V_{ABFS} +4 \cdot V_{HDES} + V_{EFGHS}$ $= 4\cdot 33\dfrac{1}{3}+4\cdot \dfrac{40}{3}+ \dfrac{32}{3}$ $=197\dfrac{1}{3}\,\text{[VE]}.$

Die Koordinaten des Mittelpunktes der Kugel sind $M(0 \mid 0 \mid m)$ , da der Körper symmetrisch zur $x_1x_3$ -Ebene und zur $x_2x_3$ -Ebene ist und somit der Mittelpunkt auf der $x_3$ -Achse liegt.

Da alle Eckpunkte des Körpers auf der Kugel liegen sollen, müssen diese auch denselben Abstand zum Mittelpunkt $M$ auf der $x_3$ -Achse haben. Dieser Abstand entspricht dem Radius der Kugel.

Es gilt: $\left| \overrightarrow{MA} \right| = \left| \overrightarrow{MF} \right|.$

$\overrightarrow{MA}= \pmatrix{5-0\\5-0\\0-m}=\pmatrix{5\\5\\-m}$

$\overrightarrow{MF}= \pmatrix{0-0\\2-0\\4-m}=\pmatrix{0\\2\\4-m}$

Aus $\left| \overrightarrow{MA} \right| = \left| \overrightarrow{MF} \right|$ folgt

$m=-3,75$

Gleichung anzeigen

Für die Koordinaten des Mittelpunktes der Kugel folgt $M(0 \mid0 \mid -3,75).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?