Teil B
1
Gegeben ist die Funktion  mit
mit  und maximalem Definitionsbereich
und maximalem Definitionsbereich  .
.
Die folgende Abbildung zeigt den Graphen von
von 
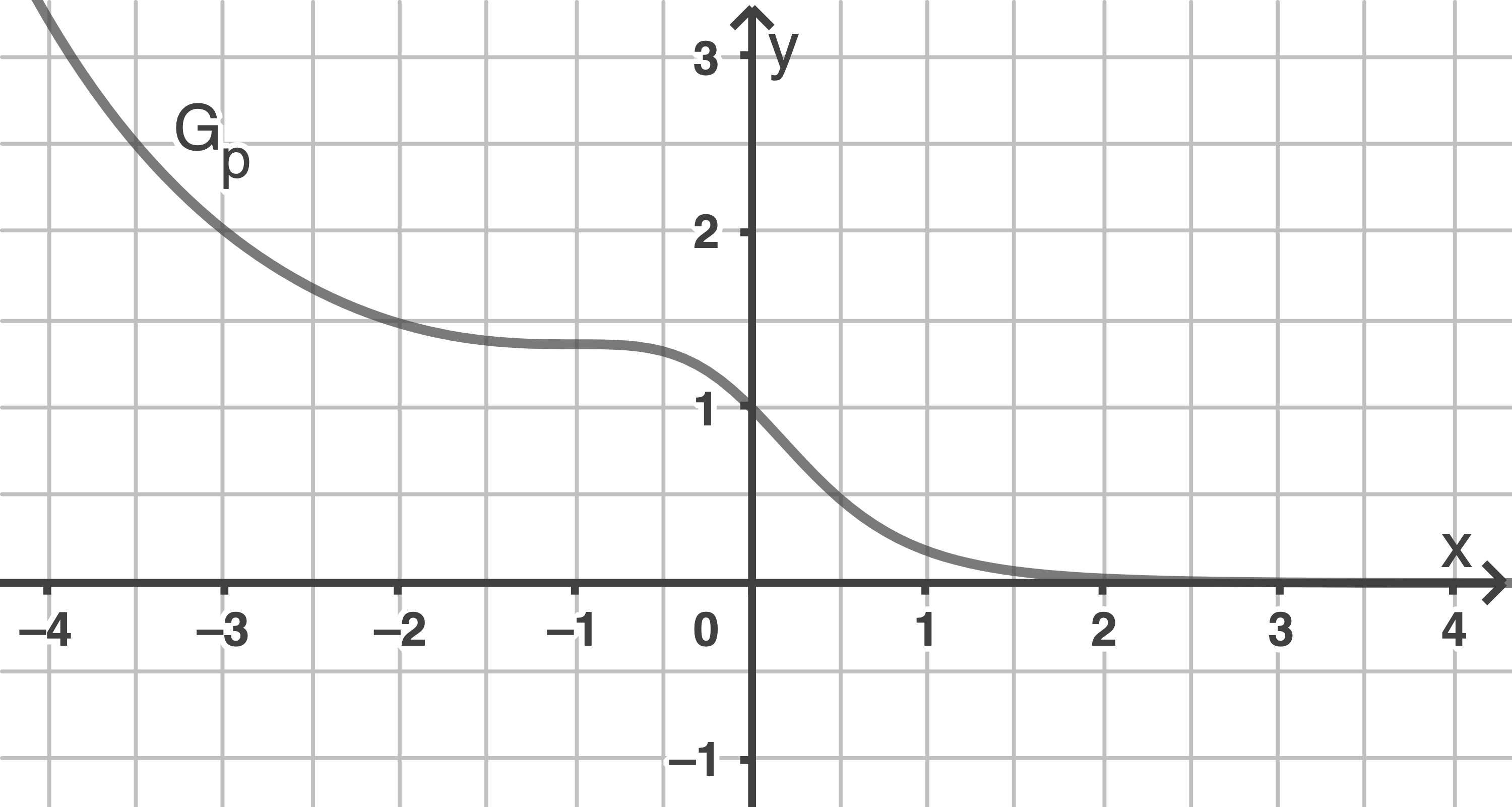
Die folgende Abbildung zeigt den Graphen

a)
Begründe jeweils anhand des Funktionsterms von  , dass
, dass  und
und  ist.
ist.
(3 BE)
b)
Weise nach, dass es genau einen Punkt gibt, in dem  eine waagrechte Tangente besitzt, der jedoch kein Extrempunkt von
eine waagrechte Tangente besitzt, der jedoch kein Extrempunkt von  ist.
ist.
(3 BE)
c)
Für die Gerade  mit der Gleichung
mit der Gleichung  mit
mit  gibt es genau zwei unterschiedliche Stellen
gibt es genau zwei unterschiedliche Stellen  sodass die folgenden vier Bedingungen erfüllt sind:
(1)
sodass die folgenden vier Bedingungen erfüllt sind:
(1) 
(2)
(3)
(4) Erläutere ohne Rechnung, welche Lagebeziehung die Gerade
Erläutere ohne Rechnung, welche Lagebeziehung die Gerade  zu
zu  hat, und zeichne
hat, und zeichne  in Abbildung 1 ein.
in Abbildung 1 ein.
(2)
(3)
(4)
(3 BE)
2
Gegeben ist die Schar der Funktionen  mit
mit  und
und  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet.
bezeichnet.
 mit
mit  und
und  wird mit
wird mit  bezeichnet, d.h.
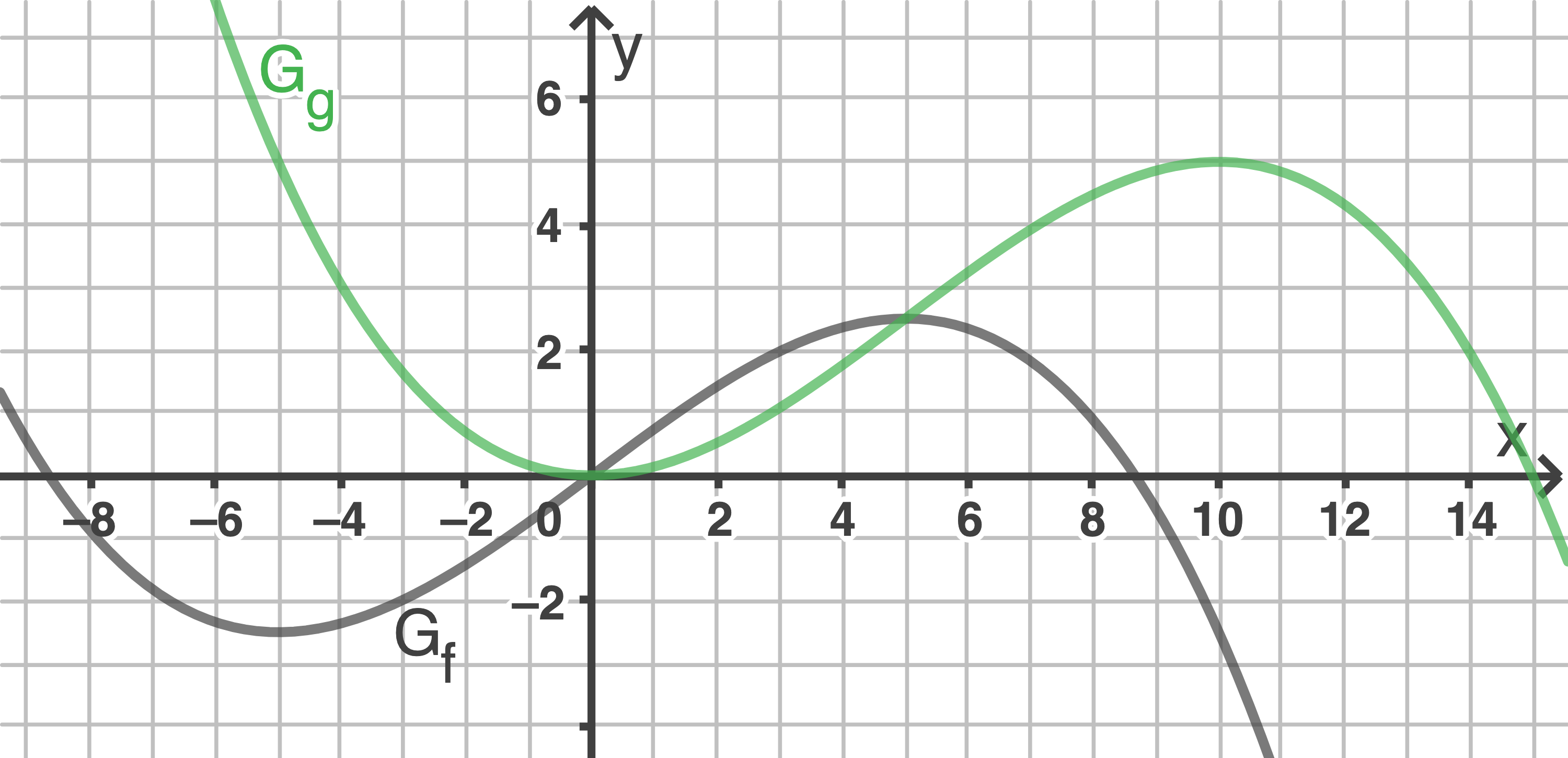
bezeichnet, d.h.  Die folgende Abbildung zeigt den Graphen
Die folgende Abbildung zeigt den Graphen  von
von 
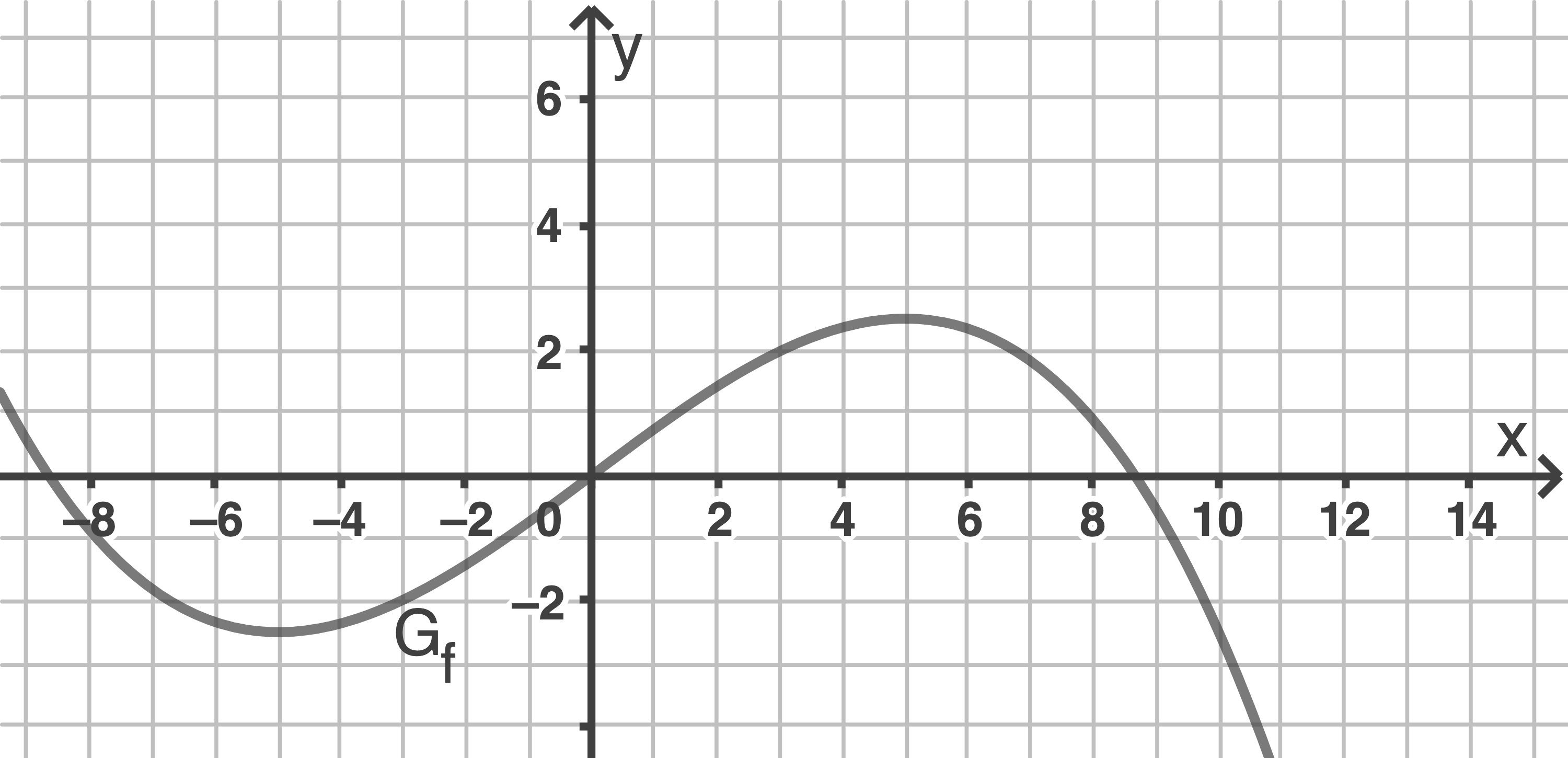
a)
Untersuche das Symmetrieverhalten von 
(2 BE)
b)
Bestimme Lage und Art der Extrempunkte von 
 zur Kontrolle: x-Koordinate des Tiefpunkts:
zur Kontrolle: x-Koordinate des Tiefpunkts: 
![\(\, \bigg ]\)](https://mathjax.schullv.de/0f419a5d021cf49991a8586047c8ad61ffa5de87c84fce9c3eefaeb61e4f8227?color=5a5a5a)
(4 BE)
c)
Für jeden vorgegebenen Wert von  kann man einen Wert für
kann man einen Wert für  finden, sodass der Inhalt der von
finden, sodass der Inhalt der von  und der x-Achse im ersten Quadranten eingeschlossenen Fläche den Wert 1 besitzt. Weise diesen Sachverhalt nach.
und der x-Achse im ersten Quadranten eingeschlossenen Fläche den Wert 1 besitzt. Weise diesen Sachverhalt nach.
(4 BE)
d)
Bestimme die Werte von  und
und  so, dass der Tiefpunkt von
so, dass der Tiefpunkt von  die Koordinaten
die Koordinaten  hat.
hat.
Die Funktion
(2 BE)

e)
Der Graph  der Funktion
der Funktion  wird aus
wird aus  durch Verschiebung erzeugt, sodass der Tiefpunkt von
durch Verschiebung erzeugt, sodass der Tiefpunkt von  im Koordinatenursprung liegt. Bestimme einen möglichen Funktionsterm von
im Koordinatenursprung liegt. Bestimme einen möglichen Funktionsterm von  und zeichne
und zeichne  in Abbildung 2 ein.
in Abbildung 2 ein.
 zur Kontrolle:
zur Kontrolle: ![\(g(x)=\dfrac{1}{100}x^2 \cdot(15-x) \bigg]\)](https://mathjax.schullv.de/dcc0d5f13a528069c2462a2f9030444bdca685e4f766fdf15f3039b2f51b4d7d?color=5a5a5a)
(4 BE)
f)
Betrachtet wird nun die in  definierte Funktion
definierte Funktion  Erläutere, aus welcher Eigenschaft von
Erläutere, aus welcher Eigenschaft von  folgt, dass
folgt, dass  an einer Stelle nicht differenzierbar ist.
an einer Stelle nicht differenzierbar ist.
Für die ersten 15 Minuten nach Einsetzen eines Starkregens wird die momentane Durchflussrate an einer Messstelle eines Hochwasserkanals mit der Funktion  modelliert. Dabei bezeichnet
modelliert. Dabei bezeichnet  die Zeit in Minuten nach Einsetzen des Starkregens und
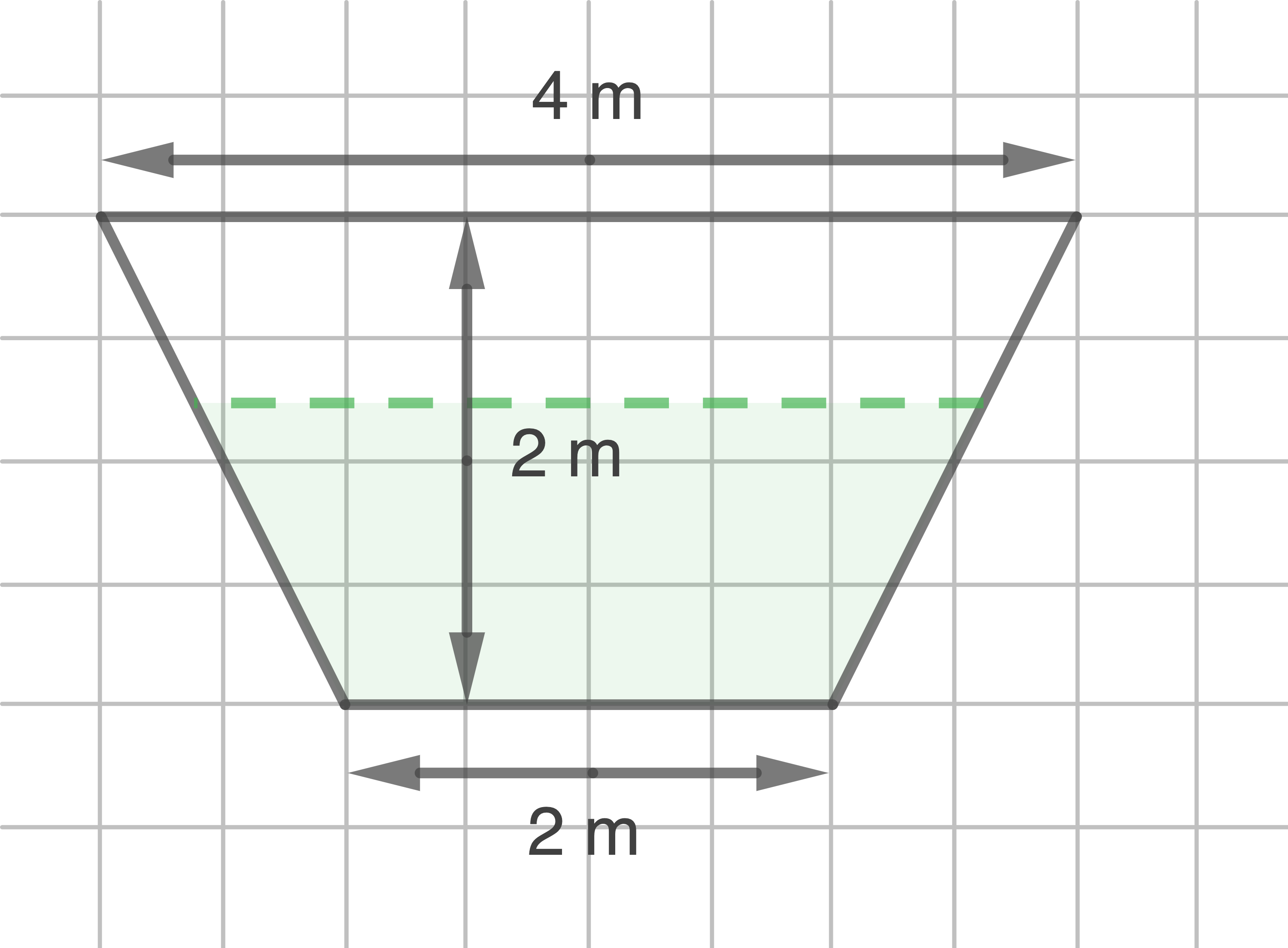
die Zeit in Minuten nach Einsetzen des Starkregens und  ) die Durchflussrate des Wasservolumens in Kubikmetern pro Sekunde. Die folgende Abbildung zeigt den Querschnitt des Kanals am Ort der Messstelle.
) die Durchflussrate des Wasservolumens in Kubikmetern pro Sekunde. Die folgende Abbildung zeigt den Querschnitt des Kanals am Ort der Messstelle.

g)
Gib für ![\(x\in [0;15]\)](https://mathjax.schullv.de/60b08fc20764f230753cbb2eeecbf1e88c342a0fb476230a80ce8efcf9a63f14?color=5a5a5a) die Lösungen der Gleichung
die Lösungen der Gleichung  an und interpretiere die Lösungen im Sachzusammenhang.
an und interpretiere die Lösungen im Sachzusammenhang.
(2 BE)
h)
Bestimme den Zeitpunkt, zu dem die momentane Änderung der Durchflussrate am größten ist.
(3 BE)
i)
Berechne das Volumen des Wassers, das in den ersten 15 Minuten nach Einsetzen des Starkregens die Messstelle passiert.
(2 BE)
j)
In einem stark vereinfachten Modell wird angenommen, dass das Wasser im Kanal gleichmäßig mit einer konstanten Geschwindigkeit von 1,5 Metern pro Sekunde fließt. Unter dieser Voraussetzung ergibt der Quotient aus der Durchflussrate und der Geschwindigkeit des Wassers die Querschnittsfläche des Wasserstroms am Ort der Messstelle (vgl. Abbildung 3). Ermittle die maximale Höhe, die der Wasserspiegel im Kanal während der ersten 15 Minuten am Ort der Messstelle erreicht.
(5 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Definitionsbereich
Für den Nenner des Funktionsterms gilt immer für alle
für alle  Zudem ist der maximale Definitionsbereich von
Zudem ist der maximale Definitionsbereich von  und somit auch
und somit auch  ebenfalls
ebenfalls 
 besitzt also keine Definitionslücken, somit ist
besitzt also keine Definitionslücken, somit ist  Grenzwert
Grenzwert
Es gilt
 Da das Wachstum der Exponentialfunktion
Da das Wachstum der Exponentialfunktion  bzw.
bzw.  deutlich stärker ist, als das des Polynoms
deutlich stärker ist, als das des Polynoms  gilt damit
gilt damit 
Für den Nenner des Funktionsterms gilt immer
Es gilt
b)
Die Lösungen der Gleichung  sind die Stellen, an denen der Graph von
sind die Stellen, an denen der Graph von  eine waagerechte Tangente besitzt. Diese Gleichung kann mit dem solve-Befehl und der Ableitungsfunktion des CAS gelöst werden.
eine waagerechte Tangente besitzt. Diese Gleichung kann mit dem solve-Befehl und der Ableitungsfunktion des CAS gelöst werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Die einzige Lösung der Gleichung
Casio Classpad II
Die einzige Lösung der Gleichung  ist
ist  Somit besitzt der Graph von
Somit besitzt der Graph von  lediglich eine Stelle mit waagerechter Tangente.
lediglich eine Stelle mit waagerechter Tangente.
Zudem ergibt sich mit dem CAS ebenfalls und
und  sodass der Graph von
sodass der Graph von  an der Stelle
an der Stelle  einen Sattelpunkt, also einen Punkt mit waagerechter Tangente aber keinen Extrempunkt besitzt.
einen Sattelpunkt, also einen Punkt mit waagerechter Tangente aber keinen Extrempunkt besitzt.
Dies ist der einzige Punkt mit waagerechter Tangente.
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

Zudem ergibt sich mit dem CAS ebenfalls
Dies ist der einzige Punkt mit waagerechter Tangente.
c)
Die Gerade  ist an zwei Stellen eine Tangente an
ist an zwei Stellen eine Tangente an 
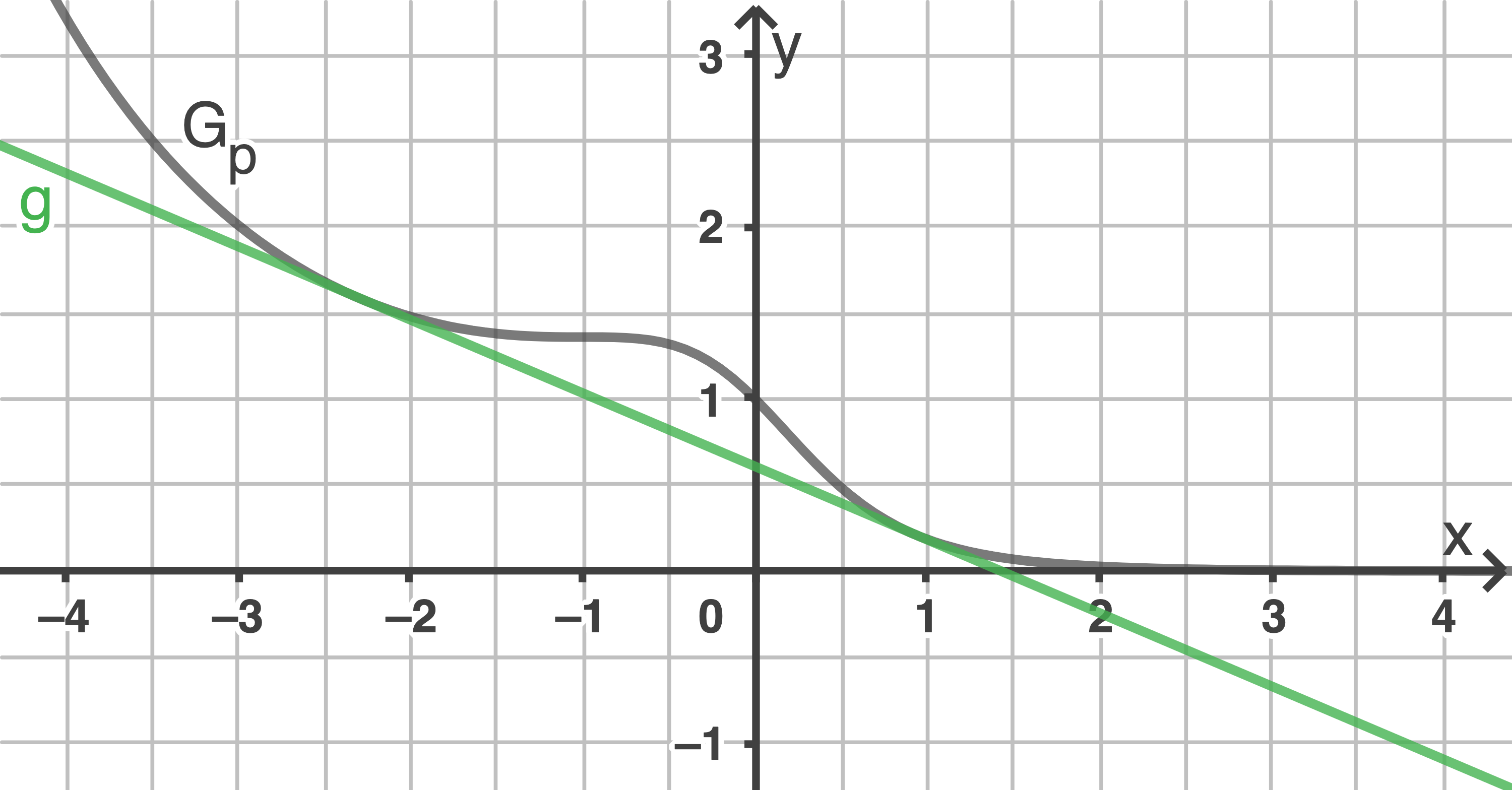

2
a)
b)
c)
Die eingeschlossene Fläche wird durch die Schnittstellen von  mit der
mit der  -Achse begrenzt. Mit dem solve-Befehl des CAS ergibt sich:
-Achse begrenzt. Mit dem solve-Befehl des CAS ergibt sich:
 für
für 
 und
und  Da die Fläche im ersten Quadranten liegen soll, werden
Da die Fläche im ersten Quadranten liegen soll, werden  und
und  betrachtet.
betrachtet.
Für den Inhalt der von und der
und der  -Achse im ersten Quadranten eingeschlossenen Fläche folgt:
-Achse im ersten Quadranten eingeschlossenen Fläche folgt:
 Eine Stammfunktion von
Eine Stammfunktion von  ist:
ist:
 Damit folgt:
Da
Damit folgt:
Da  vorgegeben ist, gibt es also für jeden Wert von
vorgegeben ist, gibt es also für jeden Wert von  einen passenden Wert von
einen passenden Wert von  nämlich
nämlich  für den die beschriebene Fläche den Inhalt 1 besitzt.
für den die beschriebene Fläche den Inhalt 1 besitzt.
Für den Inhalt der von
d)
Für die Koordinaten des Tiefpunktes gilt 
![\(\begin{array}[t]{rll}
-\sqrt{ \dfrac{a}{3}} &=& -5&\quad \scriptsize \mid\;:(-1) \mid\;^2 \\[5pt]
\dfrac{a}{3} &=& 25&\quad \scriptsize \mid\;\cdot 3 \\[5pt]
a&=&75
\end{array}\)](https://mathjax.schullv.de/fe281d372f015e96f1af50ebeed94125dcd4f9cf2c1f7024a12d4d8b954bdd58?color=5a5a5a)
![\(\begin{array}[t]{rll}
f (-5)&=& -2,5 &\quad \scriptsize \\[5pt]
75b(-5)-b(-5)^3&=& -2,5 &\quad \scriptsize \\[5pt]
-375 b+125 b&=& -2,5 &\quad \scriptsize \\[5pt]
-250 b&=& -2,5 &\quad \scriptsize \mid\;:(-250) \\[5pt]
b&=&0,01
\end{array}\)](https://mathjax.schullv.de/b2c1e51ac730707dc0c0eac73f3d46e96e53f351d66b21ad22a300eb3a919a59?color=5a5a5a) Für
Für  und
und  hat der Tiefpunkt von
hat der Tiefpunkt von  die Koordinaten
die Koordinaten 
e)
Der Graph von  wird um +5 Einheiten entlang der x-Achse und um +2,5 Einheiten entlang der y-Achse verschoben.
Daraus ergibt sich folgender Funktionsterm:
wird um +5 Einheiten entlang der x-Achse und um +2,5 Einheiten entlang der y-Achse verschoben.
Daraus ergibt sich folgender Funktionsterm:

f)
g)
Die Lösungen der Gleichung  für
für ![\([0;15]\)](https://mathjax.schullv.de/f7640cb7a533ca597f2104940149a797957b07d23031e60289fe3c69a119ec75?color=5a5a5a) sind
sind  und
und  Ca. 4,33 und 13,98 Minuten nach Einsetzen des Starkregens fließen 2 Kubikmeter Wasser pro Sekunde an der Messstelle durch den Kanal.
Ca. 4,33 und 13,98 Minuten nach Einsetzen des Starkregens fließen 2 Kubikmeter Wasser pro Sekunde an der Messstelle durch den Kanal.
h)
Die momentane Änderung der Durchflussrate wird durch die Funktion  beschrieben. Mit der Ableitungsfunktion und der Maximum-Funtion des CAS kann die Stelle bestimmt werden, an der
beschrieben. Mit der Ableitungsfunktion und der Maximum-Funtion des CAS kann die Stelle bestimmt werden, an der  für
für ![\(x\in [0;15]\)](https://mathjax.schullv.de/60b08fc20764f230753cbb2eeecbf1e88c342a0fb476230a80ce8efcf9a63f14?color=5a5a5a) maximal wird.
maximal wird.
 TI nspire CAS
TI nspire CAS

 Casio Classpad II
Casio Classpad II

 5 Minuten nach Einsetzen des Starkregens ist die momentane Änderung der Durchflussrate am größten.
5 Minuten nach Einsetzen des Starkregens ist die momentane Änderung der Durchflussrate am größten.
i)
In den ersten 15 Minuten passieren ca. 42,2 Kubikmeter Wasser die Messstelle.
j)
Für den Flächeninhalt der Querschnittsfläche des Wasserstroms am Ort der Messstelle kann die folgende Funktionsgleichung aufgestellt werden:
![\(\begin{array}[t]{rll}
A_Q(x) &=& \dfrac{g(x)}{1,5} \\[5pt]
&=& \dfrac{ \dfrac{1}{100}x^2 (15-x)}{1,5}\\[5pt]
&=& \dfrac{x^2 (15-x)}{150} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/031414b2233e7ebd788a1139e9d71faeafe638fe7e191b07071f79b1668b3b1b?color=5a5a5a) Mit dem fMax-Befehl des CAS folgt
Mit dem fMax-Befehl des CAS folgt  und
und  Der maximale Flächeninhalt der Querschnittsfläche des Wasserstroms beträgt also
Der maximale Flächeninhalt der Querschnittsfläche des Wasserstroms beträgt also  Die Querschnittsfläche hat die Form eines Trapezes. Es gilt also:
Die Querschnittsfläche hat die Form eines Trapezes. Es gilt also:
 mit
mit  Je höher der Wasserspiegel ist, desto größer ist auch
Je höher der Wasserspiegel ist, desto größer ist auch 
 hängt linear von
hängt linear von  ab. Aus der Abbildung lässt sich entnehmen, dass gilt:
Für
ab. Aus der Abbildung lässt sich entnehmen, dass gilt:
Für  ist
ist  und für
und für  ist
ist  Also gilt
Also gilt  Einsetzen liefert:
Da die Höhe nicht negativ sein kann, beträgt die maximale Höhe des Wasserspiegels am Ort der Messstelle während der ersten 15 Minuten ca. 2,27 Meter.
Einsetzen liefert:
Da die Höhe nicht negativ sein kann, beträgt die maximale Höhe des Wasserspiegels am Ort der Messstelle während der ersten 15 Minuten ca. 2,27 Meter.