Teil B
1
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet.
bezeichnet.
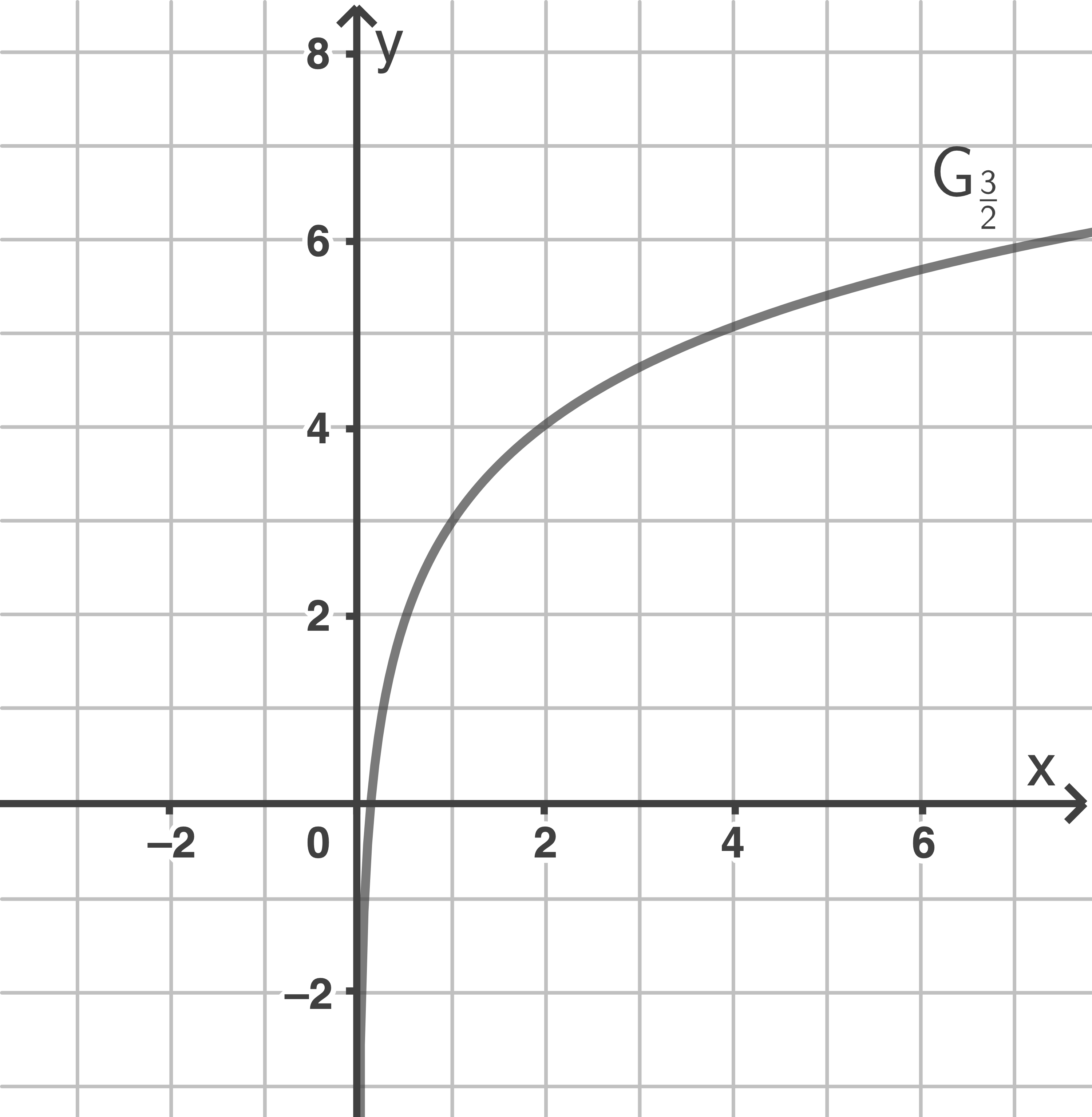
 und der Graph von
und der Graph von  schließen ein Flächenstück ein, das von einer Gerade mit der Gleichung
schließen ein Flächenstück ein, das von einer Gerade mit der Gleichung  mit
mit  in zwei Flächenstücke gleichen Inhalts zerlegt wird. Ermittle
in zwei Flächenstücke gleichen Inhalts zerlegt wird. Ermittle  auf zwei Dezimalen genau.
auf zwei Dezimalen genau.
a)
Beschreibe, wie  aus dem Graphen der in
aus dem Graphen der in  definierten Funktion
definierten Funktion  hervorgeht, und gib die Wertemenge von
hervorgeht, und gib die Wertemenge von  an.
an.
(3 BE)
b)
Zeige, dass es genau einen Punkt gibt, durch den die Graphen aller Funktionen der Schar verlaufen, und gib dessen Koordinaten an.
(3 BE)
c)
Weise nach, dass die Steigungen der Graphen  im jeweiligen Schnittpunkt von
im jeweiligen Schnittpunkt von  mit der x-Achse den Wert 3e nicht unterschreiten.
mit der x-Achse den Wert 3e nicht unterschreiten.
(6 BE)
d)
Begründe, dass alle Funktionen der Schar umkehrbar sind.
(2 BE)
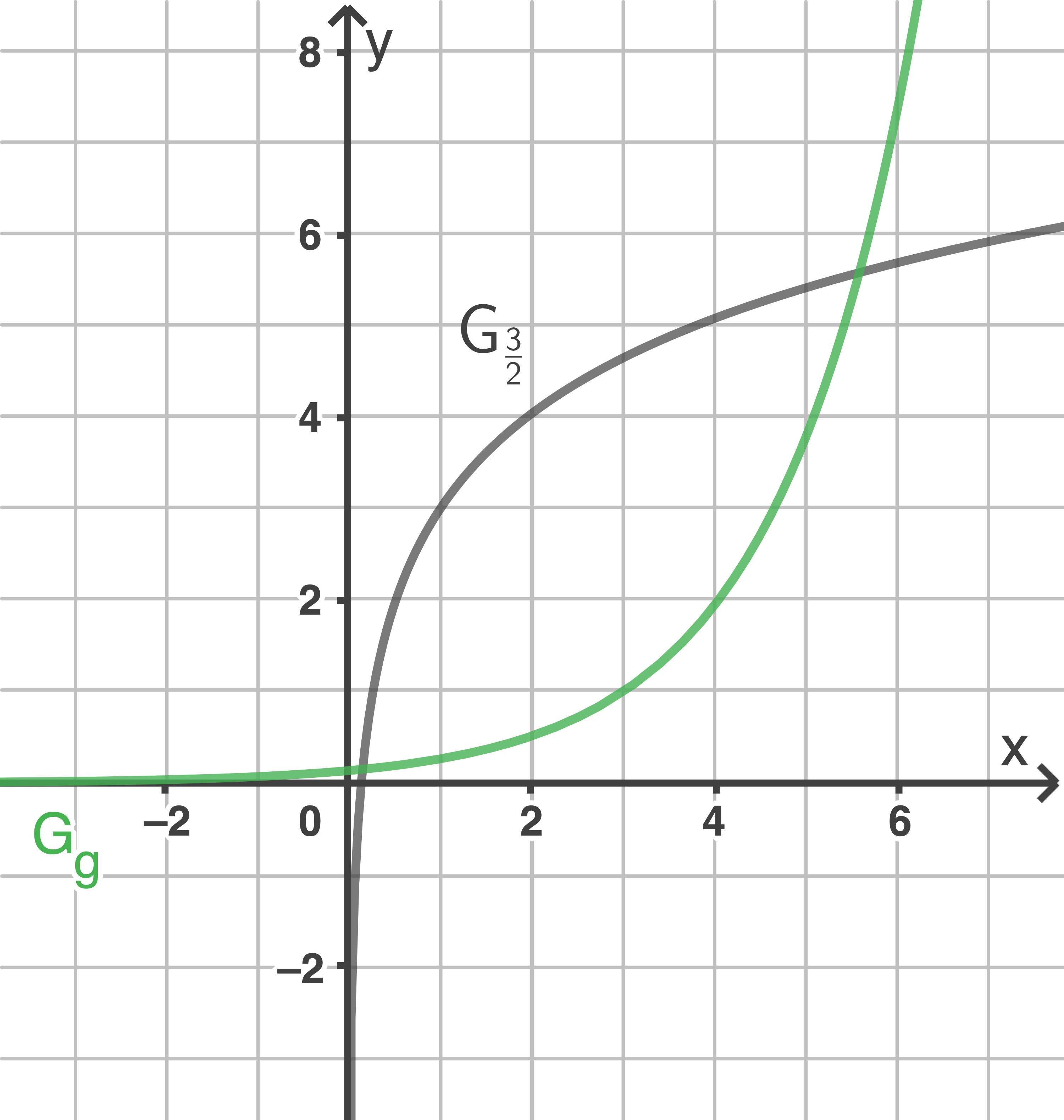
Die Abbildung zeigt den Graphen  der Funktion
der Funktion  Die Umkehrfunktion von
Die Umkehrfunktion von  wird mit
wird mit  bezeichnet.
bezeichnet.

e)
Ergänze den Graphen von  in der Abbildung.
in der Abbildung.
(2 BE)
f)
(6 BE)
2
In der Umgebung einer Schallquelle gibt der Term  für
für  näherungsweise die Lautstärke in Dezibel (dB) in Abhängigkeit vom Abstand
näherungsweise die Lautstärke in Dezibel (dB) in Abhängigkeit vom Abstand  zur Schallquelle in Metern an. In der Regel können Geräusche mit Lautstärken von mehr als 0 dB vom Menschen wahrgenommen werden, ab einer Lautstärke von etwa 100 dB werden Geräusche als unangenehm empfunden. Eine Person befindet sich in der Nähe der Schallquelle.
zur Schallquelle in Metern an. In der Regel können Geräusche mit Lautstärken von mehr als 0 dB vom Menschen wahrgenommen werden, ab einer Lautstärke von etwa 100 dB werden Geräusche als unangenehm empfunden. Eine Person befindet sich in der Nähe der Schallquelle.
 die Position der Schallquelle darstellt. Die Positionen der Person werden im Modell durch die auf der x-Achse befindlichen Punkte
die Position der Schallquelle darstellt. Die Positionen der Person werden im Modell durch die auf der x-Achse befindlichen Punkte  mit
mit ![\(u \in [-50;100]\)](https://mathjax.schullv.de/b9d2876a3a9f972f88a980cfa56794c09f1776f6b67297f501ca20f8479e34c2?color=5a5a5a) angegeben.
angegeben.
 definierte Funktion
definierte Funktion  ordnet jedem Wert von
ordnet jedem Wert von  die Lautstärke in Dezibel am Punkt
die Lautstärke in Dezibel am Punkt  zu.
zu.
a)
Die Person vergrößert ihren Abstand zur Schallquelle von 10 m auf 30 m. Berechne, um wie viele Dezibel sich die Lautstärke verändert, die die Person dabei wahrnimmt.
(2 BE)
b)
Bestimme näherungsweise denjenigen Wert von  , für den
, für den  gilt, und beschreibe die Bedeutung dieses Werts im Sachzusammenhang.
gilt, und beschreibe die Bedeutung dieses Werts im Sachzusammenhang.
Die Person bewegt sich entlang eines Wegs, der an der Schallquelle vorbeiführt. Die Situation wird in einem zweidimensionalen Koordinatensystem mit der Längeneinheit 1 m modelliert, wobei der Punkt
(2 BE)
c)
Begründe, dass der Term  in Abhängigkeit von
in Abhängigkeit von  den Abstand der Person von der Schallquelle in Metern beschreibt.
den Abstand der Person von der Schallquelle in Metern beschreibt.
Die in
(3 BE)
d)
Gib die größte Lautstärke in Dezibel an, die die Person entlang des Wegs wahrnimmt.
(2 BE)
e)
Ermittle die Länge des Wegabschnitts, auf dem die Lautstärke die Unbehaglichkeitsschwelle von 100 dB übersteigt.
(3 BE)
f)
Der Graph der Funktion  besitzt für
besitzt für  genau einen Wendepunkt. Bestimme dessen Koordinaten und die Steigung der zugehörigen Wendetangente jeweils auf eine Dezimale genau. Beschreibe die Bedeutung dieser drei Werte sowie die Bedeutung des Wendepunkts im Sachzusammenhang.
genau einen Wendepunkt. Bestimme dessen Koordinaten und die Steigung der zugehörigen Wendetangente jeweils auf eine Dezimale genau. Beschreibe die Bedeutung dieser drei Werte sowie die Bedeutung des Wendepunkts im Sachzusammenhang.
(6 BE)
Hinweis: Führe die Berechnung mit dem CAS näherungsweise durch.
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
f_{a_1}(x) &=& f_{a_2}(x) \\[5pt]
a_1\cdot \ln(x) +3 &=& a_2\cdot \ln(x) +3 \quad \scriptsize \mid\; -3 \\[5pt]
a_1\cdot \ln(x) &=& a_2\cdot \ln(x) \\[5pt]
\end{array}\)](https://mathjax.schullv.de/77a0f7bf173dd69f1f1813816a435f3d1382af0d28bf3e088d8e55927a4fa928?color=5a5a5a) Wegen
Wegen  ist dies nur für
ist dies nur für  erfüllt, also für
erfüllt, also für  Dies gilt für alle Paare
Dies gilt für alle Paare  und
und  mit
mit 
Es gilt Also haben alle Funktionen der Schar genau einen Punkt gemeinsam undzwar den Punkt
Also haben alle Funktionen der Schar genau einen Punkt gemeinsam undzwar den Punkt 
Es gilt
c)
Für die Schnittstellen von  mit der
mit der  -Achse folgt:
-Achse folgt:
![\(\begin{array}[t]{rll}
0&=& f_a(x) \\[5pt]
0&=& a \cdot \ln(x)+3&\quad \scriptsize \mid\;-3 \; \mid\, :a \\[5pt]
-\dfrac{3}{a}&=& \ln(x)&\quad \scriptsize \mid\;\mathrm{e} \\[5pt]
\mathrm{e}^{ -\frac{3}{a}}&=&x
\end{array}\)](https://mathjax.schullv.de/2583ae59db502e22892db001d60bd3ff4de1270dfe156bfd8756ad893f10954d?color=5a5a5a) Die Steigung des Graphen
Die Steigung des Graphen  wird durch
wird durch  beschrieben:
beschrieben:

 Damit lässt sich folgendes zeigen:
Damit lässt sich folgendes zeigen:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/82953ca003f67981c0c58f288513375e25d3b564d445b1db2017885b49fde3b3?color=5a5a5a) Dies ist aufgrund der Eigenschaften der
Dies ist aufgrund der Eigenschaften der  Funktion für alle
Funktion für alle  erfüllt, sodass die Steigung von
erfüllt, sodass die Steigung von  im Schnittpunkt mit der
im Schnittpunkt mit der  -Achse den Wert
-Achse den Wert  nicht unterschreitet.
nicht unterschreitet.
d)
Da die Funktion  streng monoton steigend und damit umkehrbar ist, gilt dies auch für
streng monoton steigend und damit umkehrbar ist, gilt dies auch für  da der zugehörige Graph lediglich durch Streckung/Stauchung und Verschiebung aus
da der zugehörige Graph lediglich durch Streckung/Stauchung und Verschiebung aus  hervorgeht.
hervorgeht.
e)
In der folgenden Abbildung wird der Graph von  mit
mit  bezeichnet.
bezeichnet.

f)
1. Umkehrfunktion
![\(\begin{array}[t]{rll}
y &=& \frac{3}{2}\cdot \ln(x)+3 &\quad \scriptsize \mid\; -3\\[5pt]
y-3 &=& \frac{3}{2}\cdot \ln(x) &\quad \scriptsize \mid\;\cdot \frac{2}{3} \\[5pt]
\frac{2}{3}\cdot (y-3) &=& \ln(x) &\quad \scriptsize \mid\;\mathrm e \\[5pt]
\mathrm e^{\frac{2}{3}\cdot (y-3)} &=& x
\end{array}\)](https://mathjax.schullv.de/88d2dbe3929564d4852dd24d315863d57ccf9eff0ab759f679e538342d540126?color=5a5a5a) Mit dem Variablentausch folgt dann:
Mit dem Variablentausch folgt dann:
 2. Schnittstellen
2. Schnittstellen
Aus folgen mit dem solve-Befehl des CAS die Lösungen
folgen mit dem solve-Befehl des CAS die Lösungen  und
und  3. Flächeninhalt der eingeschlossenen Fläche
3. Flächeninhalt der eingeschlossenen Fläche
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Wert b
Gesucht ist
Casio Classpad II
Wert b
Gesucht ist  mit
mit

 Mit dem solve-Befehl des CAS folgt
Mit dem solve-Befehl des CAS folgt 
Aus
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

2
a)
Für  gilt
gilt  und für
und für  gilt
gilt  Die Lautstärke ändert sich um
Die Lautstärke ändert sich um 
b)
Mit dem solve-Befehl des CAS ergibt sich für  die Lösung
die Lösung  Im Sachzusammenhang bedeutet dies, dass das Geräusch ab einer Entfernung von ca. 8,32 km nicht mehr vom Menschen wahrgenommen werden kann.
Im Sachzusammenhang bedeutet dies, dass das Geräusch ab einer Entfernung von ca. 8,32 km nicht mehr vom Menschen wahrgenommen werden kann.
c)
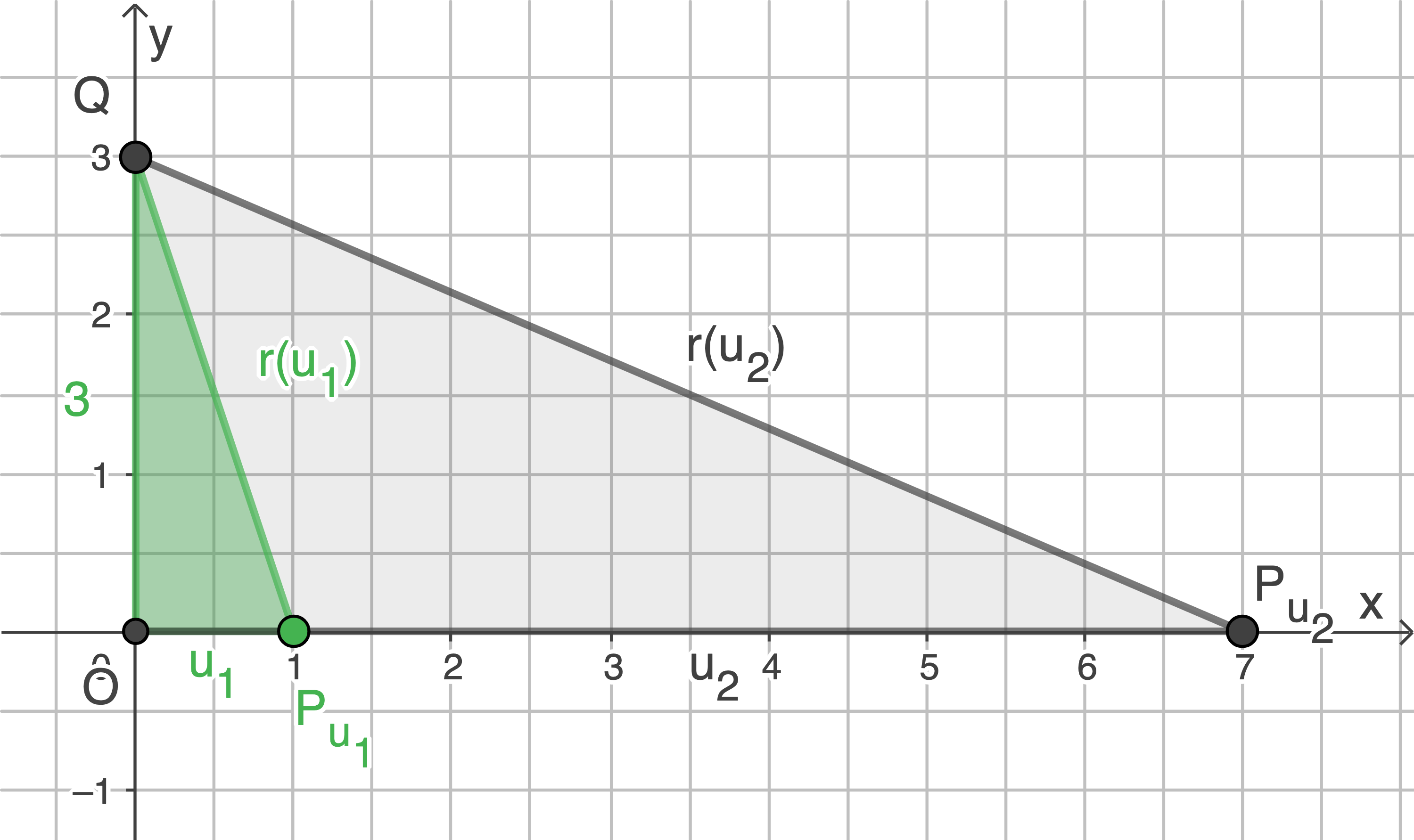
Mit dem Satz des Pythagoras gilt: Es ist
d)
Die größte Lautstärke nimmt die Person in der Position wahr, in der sie den kürzesten Abstand zur Schallquelle hat.
Dieser Punkt wird durch mit
mit  beschrieben. Mit dem CAS ergibt sich:
beschrieben. Mit dem CAS ergibt sich:
 Die größte Lautstärke, die die Person wahrnimmt beträgt 110,44 dB.
Die größte Lautstärke, die die Person wahrnimmt beträgt 110,44 dB.
Dieser Punkt wird durch
e)
Mit dem CAS ergeben sich für  die Lösungen
die Lösungen  Der Wegabschnitt, auf dem die Lautstärke 100 dB übersteigt, ist ca.
Der Wegabschnitt, auf dem die Lautstärke 100 dB übersteigt, ist ca.  lang.
lang.
f)
Wendestellen von  sind Extremstellen von
sind Extremstellen von  Mit dem Grafik-Menü des CAS können die Koordinaten der Extrempunkte des Graphen von
Mit dem Grafik-Menü des CAS können die Koordinaten der Extrempunkte des Graphen von  näherungsweise bestimmt werden.
näherungsweise bestimmt werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Mit dem CAS ergibt sich für
Casio Classpad II
Mit dem CAS ergibt sich für  ein Tiefpunkt näherungsweise mit den Koordinaten
ein Tiefpunkt näherungsweise mit den Koordinaten  Zudem gilt
Zudem gilt  Die Koordinaten des Wendepunkts des Graphen von
Die Koordinaten des Wendepunkts des Graphen von  für
für  lauten
lauten  Die Steigung der zugehörigen Wendetangente beträgt ca.
Die Steigung der zugehörigen Wendetangente beträgt ca.  Bedeutung im Sachzusammenhang
Die Wendestelle beschreibt die Stelle des Weges, an der die Lautstärke am stärksten abnimmt. Diese Stelle befindet sich 3 Meter vom Punkt mit der größten Lautstärke entfernt. Die Lautstäke beträgt hier noch ca. 107,4 dB. Die Lautstärke nimmt an dieser Stelle mit ca. 1,5 dB pro Meter ab.
Bedeutung im Sachzusammenhang
Die Wendestelle beschreibt die Stelle des Weges, an der die Lautstärke am stärksten abnimmt. Diese Stelle befindet sich 3 Meter vom Punkt mit der größten Lautstärke entfernt. Die Lautstäke beträgt hier noch ca. 107,4 dB. Die Lautstärke nimmt an dieser Stelle mit ca. 1,5 dB pro Meter ab.
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

menu  6: Graph analysieren
6: Graph analysieren  2: Minimum
2: Minimum
Analyse  Grafische Lösung
Grafische Lösung  Minimum
Minimum