Teil A
Wird der Punkt 
an der Ebene 
gespiegelt, so ergibt sich der Punkt 
a)
Bestimme eine Gleichung von in Koordinatenform.
(3 BE)
b)
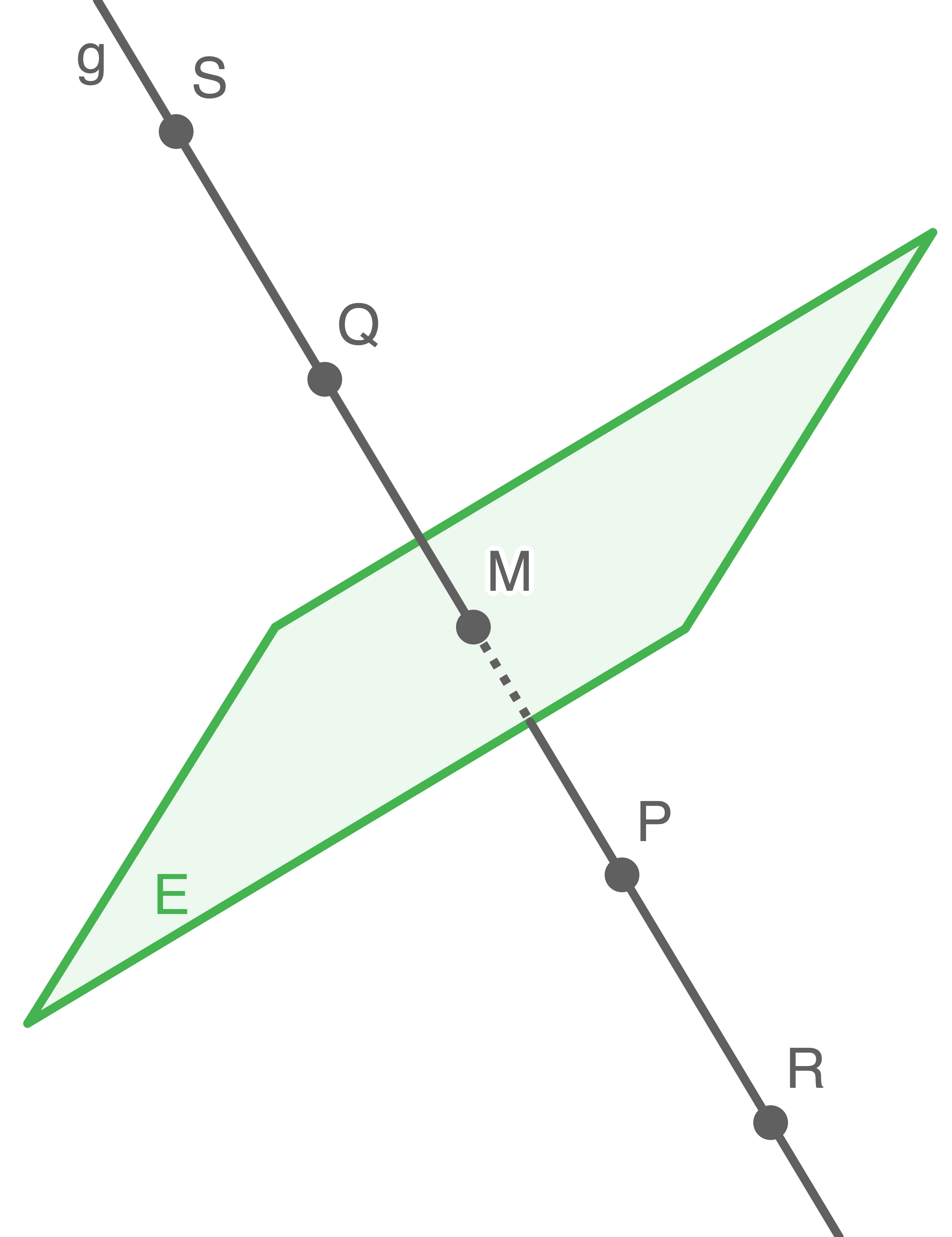
Auf der Gerade durch 
und 
liegen die Punkte 
und 
symmetrisch bezüglich 
dabei liegt bezüglich auf der gleichen Seite wie 
Der Abstand von und ist doppelt so groß wie der Abstand von und 
Bestimme die Koordinaten von
Bestimme die Koordinaten von
(2 BE)
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
1. Schritt: Einen Normalenvektor von bestimmen
Ein Normalenvektor von ist gegeben durch 
2. Schritt: Punkt aus ermitteln
Der Mittelpunkt 
der Strecke 
liegt in der Ebene 
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OP}+\dfrac{1}{2}\cdot \overrightarrow{PQ} & \\[5pt]
&=&\pmatrix{1\\2\\3}+\dfrac{1}{2}\cdot \pmatrix{6\\0\\8} & \\[5pt]
&=&\pmatrix{4\\2\\7}
\end{array}\)](https://mathjax.schullv.de/de42f0308592c2f9444b185dabde40a002f206b75e2a1441c46561dc31332e0b?color=5a5a5a)
3. Schritt: in einsetzen
![\(\begin{array}[t]{rll}
E: 6\cdot x_1+8\cdot x_3+c&=&0 & \\[5pt]
6\cdot 4+8\cdot 7+c&=&0 & \\[5pt]
80+c&=&0 &\quad \scriptsize \mid\;-80 \\[5pt]
c&=&-80
\end{array}\)](https://mathjax.schullv.de/462d8e293fdf2c744711de642c8785d91b7528d97ac607eaeda6e448ef6838ab?color=5a5a5a)
Eine Gleichung von in Koordinatenform ergibt sich somit zu:
b)
