Teil B
Gegeben sind in einem kartesischen Koordinatensystem die Ebene  und die Gerade
und die Gerade 

a)
Erläutere, warum die folgende Rechnung ein Nachweis dafür ist, dass  und
und  genau einen gemeinsamen Punkt haben:
genau einen gemeinsamen Punkt haben:

(1 BE)
b)
Berechne die Größe des Schnittwinkels von  und
und  und zeige, dass
und zeige, dass  der Schnittpunkt von
der Schnittpunkt von  und
und  ist.
ist.
(5 BE)
c)
Die Kugel  mit dem Mittelpunkt
mit dem Mittelpunkt  berührt die Ebene
berührt die Ebene 
Bestimme die Koordinaten des zugehörigen Berührpunkts sowie den Kugelradius
sowie den Kugelradius  [zur Kontrolle:
[zur Kontrolle:  ,
,  ]
]
Bestimme die Koordinaten des zugehörigen Berührpunkts
(6 BE)
d)
Weise nach, dass die Gerade  die Kugel
die Kugel  im Punkt
im Punkt  berührt.
berührt.
(5 BE)
Die Punkte  und
und  (vgl. die Aufgaben b,c und d) liegen in einer Ebene
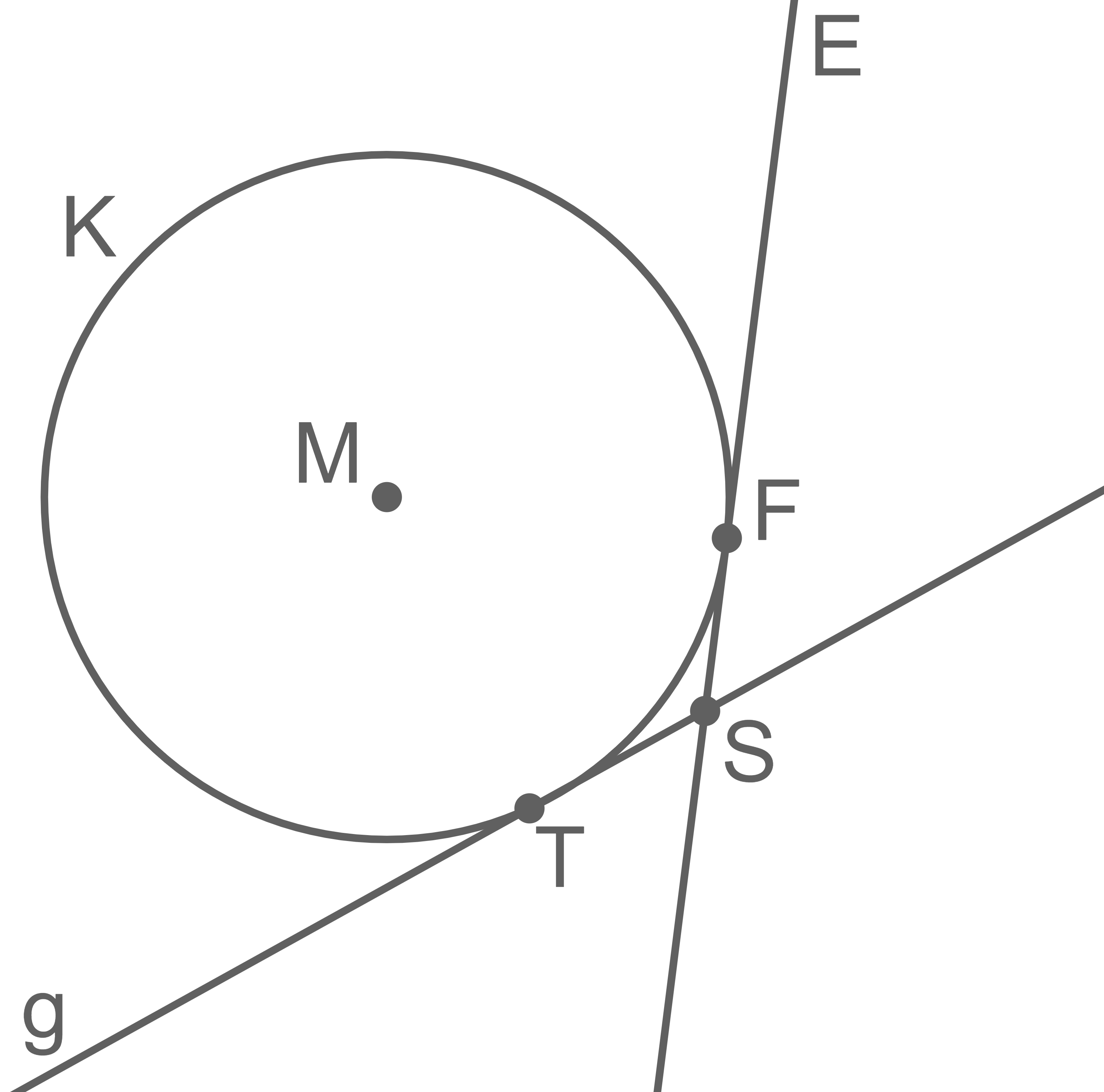
(vgl. die Aufgaben b,c und d) liegen in einer Ebene  Die nicht maßstabsgetreue Abbildung zeigt die Gerade
Die nicht maßstabsgetreue Abbildung zeigt die Gerade  den Schnitt der Ebene
den Schnitt der Ebene  mit der Ebene
mit der Ebene  sowie den Schnitt der Kugel
sowie den Schnitt der Kugel  mit der Ebene
mit der Ebene 
e)
Begründe, dass das Viereck  einen Umkreis besitzt. Berechne den Flächeninhalt dieses Vierecks.
einen Umkreis besitzt. Berechne den Flächeninhalt dieses Vierecks.
(4 BE)

f)
Durch Rotation des Vierecks  um die Gerade
um die Gerade  entsteht ein Körper. Beschreibe diesen Körper.
entsteht ein Körper. Beschreibe diesen Körper.
In einer Formelsammlung ist zur Berechnung des Volumens eines solchen Körpers die Formel zu finden.
zu finden.
Gib für den beschriebenen Körper die Strecken an, deren Längen für bzw.
bzw.  einzusetzen sind.
einzusetzen sind.
In einer Formelsammlung ist zur Berechnung des Volumens eines solchen Körpers die Formel
Gib für den beschriebenen Körper die Strecken an, deren Längen für
(4 BE)
(25 BE)
a)
Die Rechnung zeigt, dass das Skalarprodukt des Richtungsvektors der Gerade  mit dem Normalenvektor der Ebene
mit dem Normalenvektor der Ebene  nicht Null ergibt, das heißt die beiden Vektoren stehen nicht senkrecht aufeinander.
nicht Null ergibt, das heißt die beiden Vektoren stehen nicht senkrecht aufeinander.
Somit liegt die Gerade weder in der Ebene, noch verläuft sie parallel zu dieser, das heißt und
und  schneiden sich in genau einem Punkt.
schneiden sich in genau einem Punkt.
Somit liegt die Gerade weder in der Ebene, noch verläuft sie parallel zu dieser, das heißt
b)
Größe des Schnittwinkels berechnen
Schnittpunkt zeigen
Ein allgemeiner Punkt auf  hat die folgenden Koordinaten:
hat die folgenden Koordinaten:
 Einsetzen in die Ebenengleichung von
Einsetzen in die Ebenengleichung von  liefert:
Einsetzen von
liefert:
Einsetzen von  in die Geradengleichung liefert weiter:
in die Geradengleichung liefert weiter:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=&\pmatrix{3\\12\\-2} -0,5 \pmatrix{5\\11\\-4} \\[5pt]
&=&\pmatrix{0,5\\6,5\\0}
\end{array}\)](https://mathjax.schullv.de/68bc131249531aee383f6d97a6f44cd2153e92ec8722e90722d23f01dbe05085?color=5a5a5a) Die Koordinaten des Schnittpunkts sind somit gegeben durch
Die Koordinaten des Schnittpunkts sind somit gegeben durch 
c)
Die Kugel berührt die Ebene in nur einem Punkt. Der Radius  ergibt sich somit als der Abstand des Mittelpunktes
ergibt sich somit als der Abstand des Mittelpunktes  zur Ebene
zur Ebene 
![\(\begin{array}[t]{rll}
r&=&d(M,E) \\[5pt]
&=&\dfrac{\vert 4 \cdot(-13) -8 \cdot 20 +50 \vert}{\sqrt{4^2+8^2+1^2}} \\[5pt]
&=&\dfrac{162}{9} \\[5pt]
&=&18
\end{array}\)](https://mathjax.schullv.de/c84cca51dc1bd8105ebea6ea50dd99425232da190ee988e57da9f86f5dae3342?color=5a5a5a) Der Vektor
Der Vektor  ist ein Vielfaches des Normalenvektors der Ebene und besitzt die Länge
ist ein Vielfaches des Normalenvektors der Ebene und besitzt die Länge  somit folgt für den Ortsvektor des Berührpunkts
somit folgt für den Ortsvektor des Berührpunkts  Der Berührpunkt
Der Berührpunkt  besitzt somit die Koordinaten
besitzt somit die Koordinaten 
d)
Mit dem Radius und den Koordinaten von  folgt für die Kugelgleichung von
folgt für die Kugelgleichung von 

 Einsetzen der Koordinaten eines allgemeinen Punktes auf
Einsetzen der Koordinaten eines allgemeinen Punktes auf  in die Kugelgleichung liefert:
Die einzige Lösung ist somit
in die Kugelgleichung liefert:
Die einzige Lösung ist somit  das heißt die Gerade berührt die Kugel. Einsetzen in die allgemeinen Koordinaten eines Punktes der Geraden
das heißt die Gerade berührt die Kugel. Einsetzen in die allgemeinen Koordinaten eines Punktes der Geraden  liefert für die Koordinaten des Berührpunkts
liefert für die Koordinaten des Berührpunkts 

e)
Existenz eines Umkreises begründen
Das Viereck  hat die Form eines Drachens der symmetrisch bezüglich der Strecke
hat die Form eines Drachens der symmetrisch bezüglich der Strecke ![\([MS]\)](https://mathjax.schullv.de/50de47d525eabb2d2399d53b7837a9a6c566bf7edba372fce1209310fcc7d3d9?color=5a5a5a) ist. Da die Ebene
ist. Da die Ebene  und die Gerade
und die Gerade  die Kugel
die Kugel  in
in  bzw.
bzw.  berühren, besitzt das Viereck
berühren, besitzt das Viereck  bei
bei  und
und  einen rechten Winkel. Die beiden Dreiecke
einen rechten Winkel. Die beiden Dreiecke  und
und  sind somit jeweils rechtwinklig mit der Grundseite
sind somit jeweils rechtwinklig mit der Grundseite ![\([MS]\)](https://mathjax.schullv.de/50de47d525eabb2d2399d53b7837a9a6c566bf7edba372fce1209310fcc7d3d9?color=5a5a5a) gegenüber von dem rechten Winkel. Mit Hilfe des Satz des Thales existieren somit aufgrund der Symmetrie des Drachens zwei passende Halbkreise, die sich zu einem Umkreis des Vierecks
gegenüber von dem rechten Winkel. Mit Hilfe des Satz des Thales existieren somit aufgrund der Symmetrie des Drachens zwei passende Halbkreise, die sich zu einem Umkreis des Vierecks  zusammenfügen.
Flächeninhalt berechnen
Für die Längen
zusammenfügen.
Flächeninhalt berechnen
Für die Längen  und
und  der Diagonalen von
der Diagonalen von  gilt:
gilt:
![\(\begin{array}[t]{rll}
e&=&\left\vert\overrightarrow{MS} \right\vert \\[5pt]
&=&\left\vert\pmatrix{0,5\\6,5\\0} - \pmatrix{-13\\20\\0}\right\vert \\[5pt]
&=&\left\vert\pmatrix{13,5\\-13,5 \\ 0 }\right\vert\\[5pt]
&\approx&19,1\;[\text{LE}]
\end{array}\)](https://mathjax.schullv.de/fc55088068221ef071a5aae0d6a46cd9d349abac72782026d82579fb1cff59cd?color=5a5a5a)
![\(\begin{array}[t]{rll}
f&=&\left\vert\overrightarrow{FT} \right\vert \\[5pt]
&=&\left\vert\pmatrix{-5\\4\\2} - \pmatrix{3\\12\\-2}\right\vert \\[5pt]
&=&\left\vert\pmatrix{-8\\-8\\4}\right\vert\\[5pt]
&\approx&12\;[\text{LE}]
\end{array}\)](https://mathjax.schullv.de/6d522999ed753ad33c156bf82de86af9fba5cb84782dfe50353a6f5c157fae95?color=5a5a5a) Damit folgt für den Flächeninhalt
Damit folgt für den Flächeninhalt  des Vierecks:
des Vierecks:

![\( \approx \dfrac{1}{2} \cdot 19,1 \cdot 12 \approx 114,6 \;[\text{FE}]\)](https://mathjax.schullv.de/6c3d59e02bc29d73ac09020aa17639177f5becad8d4f5a967206c0402bcd8121?color=5a5a5a)
f)
Körper beschreiben
Durch Rotation des Vierecks  um die Gerade
um die Gerade  entsteht ein Körper bestehend aus zwei Kegeln mit Spitzen
entsteht ein Körper bestehend aus zwei Kegeln mit Spitzen  bzw.
bzw.  und gleicher Grundfläche, die an dieser aneinander geklebt werden.
Strecken angeben
Die Formel für das Volumen eines Kegels ist gegeben durch
und gleicher Grundfläche, die an dieser aneinander geklebt werden.
Strecken angeben
Die Formel für das Volumen eines Kegels ist gegeben durch  Da die beiden Kegel aus denen der Körper besteht die gleiche Grundfläche besitzen, wird für
Da die beiden Kegel aus denen der Körper besteht die gleiche Grundfläche besitzen, wird für  die Länge der Strecke
die Länge der Strecke ![\([FT]\)](https://mathjax.schullv.de/fee03ba4e091b31acdb643276f20430800aafcad1689118457eeac1ad0a09430?color=5a5a5a) und für
und für  die Summe der Höhen der beiden Kegel, das heißt die Länge der Strecke
die Summe der Höhen der beiden Kegel, das heißt die Länge der Strecke ![\([MS],\)](https://mathjax.schullv.de/c9b0ab7b1be1978bf6d3cf77c2eb7579509057d01d63553c45eb009a9bc54a45?color=5a5a5a) eingesetzt.
eingesetzt.