Teil A

Gegeben ist die Funktion $f:x \mapsto \dfrac{\mathrm{ln}x}{x^2}$ mit maximalem Definitionsbereich $D$ .

Gib $D$ sowie die Nullstelle von $f$ an und bestimme $\lim\limits_{x\to 0}\, f(x)$ .

(3 BE)

Ermittle die $x$ -Koordinate des Punkts, in dem der Graph von $f$ eine waagrechte Tangente hat.

(4 BE)

Gib jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.

Der Punkt $(2\mid 0)$ ist ein Wendepunkt des Graphen von $g$ .

(2 BE)

Der Graph der Funktion $h$ ist streng monoton fallend und rechtsgekrümmt.

(2 BE)

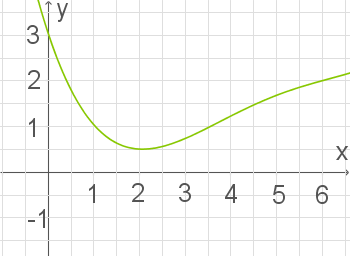
Die Abbildung 1 zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ .

Graph einer Funktion mit einem grünen Verlauf auf einem karierten Hintergrund.

Abb. 1

Bestimme mithilfe der Abbildung 1 einen Näherungswert für $\displaystyle\int_{3}^{5}\, f(x)\,\mathrm dx$ .

(2 BE)

Die Funktion $F$ ist die in $\mathbb{R}$ definierte Stammfunktion von $f$ mit $F(3) =0$

Gib mithilfe der Abbildung 1 einen Näherungswert für die Ableitung von $F$ an der Stelle $x=2$ an.

(1 BE)

Zeige, dass $F(b)=\displaystyle\int_{3}^{b}f(x)\;\mathrm dx$ mit $b\in\mathbb{R}$ gilt.

(2 BE)

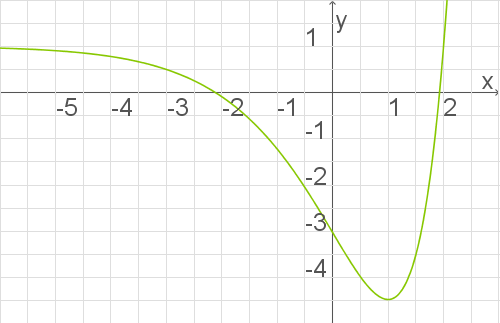
Abbildung 3 zeigt den Graphen $G_k$ einer in $\mathbb{R}$ definierten Funktion $k$ .
Skizziere in Abbildung 3 den Graphen der zugehörigen Ableitungsfunktion $k‘$ . Berücksichtige dabei insbesondere einen Näherungswert für die Steigung des Graphen $G_k$ an dessen Wendepunkt $(0 \mid -3)$ sowie die Nullstelle von $k‘$ .

Graph einer mathematischen Funktion auf einem Koordinatensystem mit Achsen und Gitterlinien.

Abb. 2

(4 BE)

(20 BE)

Bildnachweise [nach oben]

[1]

[2]

$\blacktriangleright$ Definitionsbereich bestimmen

Du sollst den Definitionsbereich $D$ der Funktion $f:\, x\mapsto\dfrac{\ln x}{x^2}$ bestimmen. Für den Definitionsbereich betrachtest du zuerst den Nenner des Bruchs $x^2$ um mögliche Definitionslücken zu bestimmen.

$\dfrac{1}{x^2}$ ist für alle $x$ außer $0$ definiert. Du erhältst einen ersten Definitionsbereich von $D_1=\mathbb{R}\setminus \{0\}$ .
Im Zähler $\ln x$ dürfen nur strickt positive Argumente verwendet werden, der Definitionsbereich des $\ln$ ist $D_2=\mathbb{R}^+=(0,\infty)$ .

Zusammenfassend ergibt sich für den gesuchten Definitionsbereich $D$ :

$\begin{array}[t]{rll} D&=& \mathbb{R}^+=(0,\infty) \end{array}$

$\blacktriangleright$ Nullstellen bestimmen

Für die Nullstellen der Funktion sind lediglich die Nullstellen des Zählers zu betrachten:

$\begin{array}[t]{rll} \ln x&=& 0 &\quad \scriptsize \mid\; e \\[5pt] x&=& e^0=1 \end{array}$

$x=1$ ist die einzige Nullstelle des $\ln$ und liegt im Definitionsbereich $D$ , somit ist sie auch Nullstelle von $f.$

$\blacktriangleright$ Grenzwert bestimmen

Du sollst den Grenzwert von $f(x)$ für $x\to 0$ bestimmen. Der Funktionsterm besteht aus einem Bruch. Überlege dir für die beiden Terme im Zähler und Nenner zunächst unabhängig den Grenzwert für $x\to 0$ .

Im Zähler steht $\ln(x)$ . Für $x=0$ ist dies nicht definiert. Du kennst aber den groben Verlauf der Logarithmusfunktion und weißt daher, dass $\ln(x)$ für $x \lt 1$ negativ ist und für immer kleinere $x$ auch immer kleiner wird, und zwar unbegrenzt. Daher gilt

$\lim\limits_{x\to0} \ln(x) = -\infty$

Im Nenner des Bruchs steht $x^2$ . Dies ist definiert, es ist $0^2 = 0$ . Es wird also sozusagen $-\infty$ durch $0$ geteilt. Es kann aber nicht durch $0$ geteilt werden. Betrachtest du also den Grenzwert, wird $-\infty$ durch einen sehr kleinen aber positiven Wert geteilt. Und daher ist:

$\lim\limits_{x\to0} \dfrac{\ln(x)}{x^2} = -\infty$ .

$\blacktriangleright$ Stelle mit waagerechter Tangente bestimmen

Du sollst die $x$ -Koordinate der Stelle bestimmen, an welcher der Graph eine waagerechte Tangente besitzt. Waagerechte Tangenten besitzen die Steigung $0$ . Gesucht ist also eine Stelle, an der der Graph von $f$ die Steigung Null besitzt. Da die erste Ableitung von $f$ die Steigung des Graphen von $f$ beschreibt, ist also eine Nullstelle der ersten Ableitung von $f$ gesucht. Bilde den Term der ersten Ableitung mit der Quotientenregel:

$\dfrac{d}{dx}\dfrac{u(x)}{v(x)}=\dfrac{u‘(x)\cdot v(x)-u(x)\cdot v‘(x)}{(v(x))^2}$

Mit $u(x)=\ln x$ und $v(x)=x^2$ ergibt sich:

$\begin{array}[t]{rll} f‘(x)&=& \dfrac{\dfrac{1}{x}\cdot x^2-\ln x \cdot 2\cdot x}{x^4} \\[5pt] &=& \dfrac{1-2\cdot \ln x}{x^3} \end{array}$

Für die Nullstelle betrachtest du lediglich den Zähler:

$\begin{array}[t]{rll} 0&=& 1-2\cdot \ln x &\quad \scriptsize \mid\; +2\cdot \ln x \\[5pt] 1&=& 2\cdot \ln x &\quad \scriptsize \mid\; :2 \\[5pt] \frac{1}{2}&=&\ln x &\quad \scriptsize \mid\; e \\[5pt] x&=&\sqrt{e} \end{array}$

Für $x=\sqrt{e}$ besitzt der Graph von $f$ eine waagerechte Tangente.

$\blacktriangleright$ Term und Definitionsbereich angeben

Du sollst den Term und den Definitionsbereich einer Funktion angeben, welche die Eigenschaft erfüllt, dass $(2\mid 0)$ ein Wendepunkt des Graphen von $g$ ist.

Für einen Wendepunkt muss die zweite Ableitung $0$ , aber nicht konstant sein. Die einfachste Form ist deshalb die Verschiebung einer Geraden. Du erhältst durch Integration, wobei $c=0$ ist:

$\begin{array}[t]{rll} g‘‘(x)&=& x-2 \\[5pt] g‘(x)&=& \frac{1}{2}\cdot x^2-2\cdot x \\[5pt] g(x)&=& \frac{1}{6}\cdot x^3 -x^2 \end{array}$

Der Graph von $g$ besitzt an der Stelle $x=2$ einen Wendepunkt. Dieser hat aber noch nicht die $y$ -Koordinate null:

$g(2)= \frac{1}{6}\cdot 2^3-2^2 =-\frac{8}{3}$

Der Graph muss also noch um $\frac{8}{3}$ Einheiten entlang der positiven $y$ -Achse verschoben werden.

Die Funktion $g_1(x)=\frac{1}{6}\cdot x^3 -x^2+\frac{8}{3}$ erfüllt die Bedingung, wobei für den Definitionsbereich $D=\mathbb{R}$ gilt.

$\blacktriangleright$ Term und Definitionsbereich angeben

Der Graph der Funktion $h$ soll streng monoton fallend und rechtsgekrümmt sein. Dies ist der Fall, wenn die zweite Ableitung negativ ist. Zudem soll der Graph von $h$ streng monoton fallend sein. Dies ist der Fall, wenn die erste Ableitung negativ ist. Eine Möglichkeit ist beispielsweise eine $\mathrm e$ -Funktion als Grundlage.

$\begin{array}[t]{rll} h‘‘(x)&=& -\mathrm e^x \lt 0 \\[5pt] h‘(x)&=& -\mathrm e^{x}\lt 0 \\[5pt] h(x)&=&-\mathrm e^{x} \end{array}$

$h(x)=-\mathrm e^{x}$ ist eine mögliche Funktion und besitzt den Definitionsbereich $D=\mathbb{R}$ .

$\blacktriangleright$ Näherungswert des Integrals bestimmen

Du sollst anhand des Funktionsgraphen einen Näherungswert für das Integral mit den Grenzen $3$ und $5$ bestimmen. Dieses Integral beschreibt den Inhalt der Fläche, die vom Graphen von $f$ , der $x$ -Achse und den Geraden mit $y = 3$ und $y =5$ eingeschlossen wird.

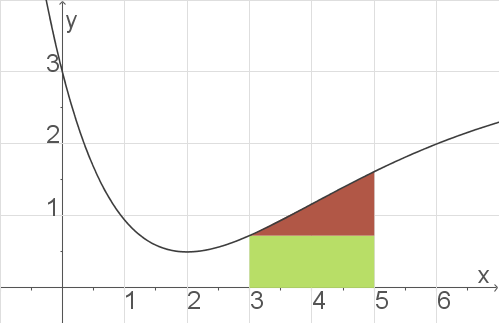Diagramm einer Funktion mit einem hervorgehobenen Bereich in verschiedenen Farben. Achsen sind beschriftet.

Abb. 1: Näherung des Integrals

Zerlege die Fläche in ein Rechteck und eine Fläche, die durch ein Dreieck angenähert werden kann. Die Näherung entspricht somit der Summe der Flächeninhalte. Für das Rechteck mit den Kantenlängen $5-3=2$ und $f(3)$ ergibt sich:

$\begin{array}[t]{rll} A_{4}&=& 2\cdot f(3) \\[5pt] &\approx& 2\cdot 0,75 \\[5pt] &=& 1,5 \end{array}$

Das rechtwinklige Dreieck hat eine Kathete mit dem Rechteck gemeinsam. Die Länge der anderen Kathete ist $f(5)-f(3)$ :

$\begin{array}[t]{rll} A_3&=& \frac{1}{2}\cdot 2\cdot (f(5)-f(3)) \\[5pt] &=& f(5)-f(3) \\[5pt] &\approx& 1,6-0,75 \\[5pt] &=& 0,85 \end{array}$

Für beide Flächen zusammen, beziehungsweise für die Näherung des Integrals, ergibt sich:

$\begin{array}[t]{rll} \int\limits_3^5 f(x)\; dx&\approx& A_4+A_3 \\[5pt] &=& 2,35 \end{array}$

Du kannst einen Näherungswert für das Integral mit ungefähr $2,35$ angeben.

$\blacktriangleright$ Wert der Ableitung bestimmen

Du sollst einen Wert für die Ableitung der Stammfunktion $F$ an der Stelle $x=2$ angeben. Da $F$ eine Stammfunktion von $f$ mit $F(3)=0$ ist, gilt:

$\begin{array}[t]{rll} F‘(x)&=& f(x) \end{array}$

Du kannst somit den Wert der Ableitung von $F$ als Funktionswert von $f$ am Graphen ablesen.

$\begin{array}[t]{rll} F‘(2)&=& f(2) \\[5pt] &\approx& 0,5 \end{array}$

Die Ableitung der Funktion $F$ an der Stelle $x=2$ beträgt ca. $0,5$ .

$\blacktriangleright$ Gleichheit zeigen

Du sollst zeigen, dass $F(b)=\int\limits_3^b f(x)\; \mathrm dx$ gilt. Du kannst hierzu den Hauptsatz der Differential- und Integralrechnung verwenden:

$\displaystyle\int_{a}^{b}f(x) \;\mathrm dx = F(b) -F(a)$

Dabei ist $F$ eine Stammfunktion von $f$ . Wende diesen Satz auf das gegebene Integral an. Zusätzlich hast du noch die Information gegeben, dass $F(3) =0$ gilt. Damit erhältst du insgesamt folgende Rechnung:

$\begin{array}[t]{rll} \displaystyle\int_{3}^{b} f(x)\; \mathrm dx&=& F(b) -F(3) &\quad \scriptsize \mid\; F(3)=0 \\[5pt] &=& F(b)-0 \\[5pt] &=& F(b) \\[5pt] \end{array}$

Damit gilt also $\displaystyle \int_3^b f(x)\; \mathrm dx = F(b)$ .

$\blacktriangleright$ Graphen der Ableitung skizzieren

Du sollst zu einem gegebenen Funktionsgraphen den Graphen der Ableitung skizzieren und dabei besonders auf die Steigung am Wendepunkt $(0\vert -3)$ und die Nullstelle von $k‘$ achten. Zeichne dir idealerweise ein paar Tangenten an den Graphen und markiere signifikante Stellen wie Wende- und Extremalstellen.

Da der Graph gegen eine waagerechte Asymptote bei $y=1$ strebt, konvergiert die Ableitung für $x\to -\infty$ gegen $0$ .
Für eine Wendestelle müssen notwendiges und hinreichendes Kriterium erfüllt sein. Das heißt, dass die zweite Ableitung an dieser Stelle einen Vorzeichenwechsel haben muss. Dies ist an einer Extremstelle der ersten Ableitung der Fall.

An der Wendestelle von $k$ muss $k‘$ also eine Extremstelle besitzen. Eine Nullstelle besitzt $k‘$ wegen des notwendigen Kriteriums für Extremstellen an der Extremstelle von $k$ , also bei $x\approx 1.$

Skizziert ergibt sich in grün der Graph der Ableitung:

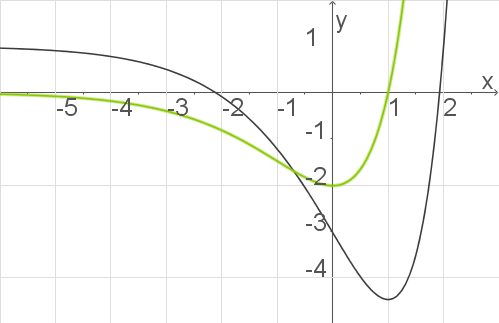Graph zweier Funktionen im Koordinatensystem mit x- und y-Achse.

Abb. 2: Ableitung skizzieren

Bildnachweise [nach oben]

[1]

[2]