Teil B
1
Die Abbildung zeigt einen Ausschnitt des Graphen  der in
der in  definierten Funktion
definierten Funktion  mit
mit 
 hat genau einen Tiefpunkt
hat genau einen Tiefpunkt 
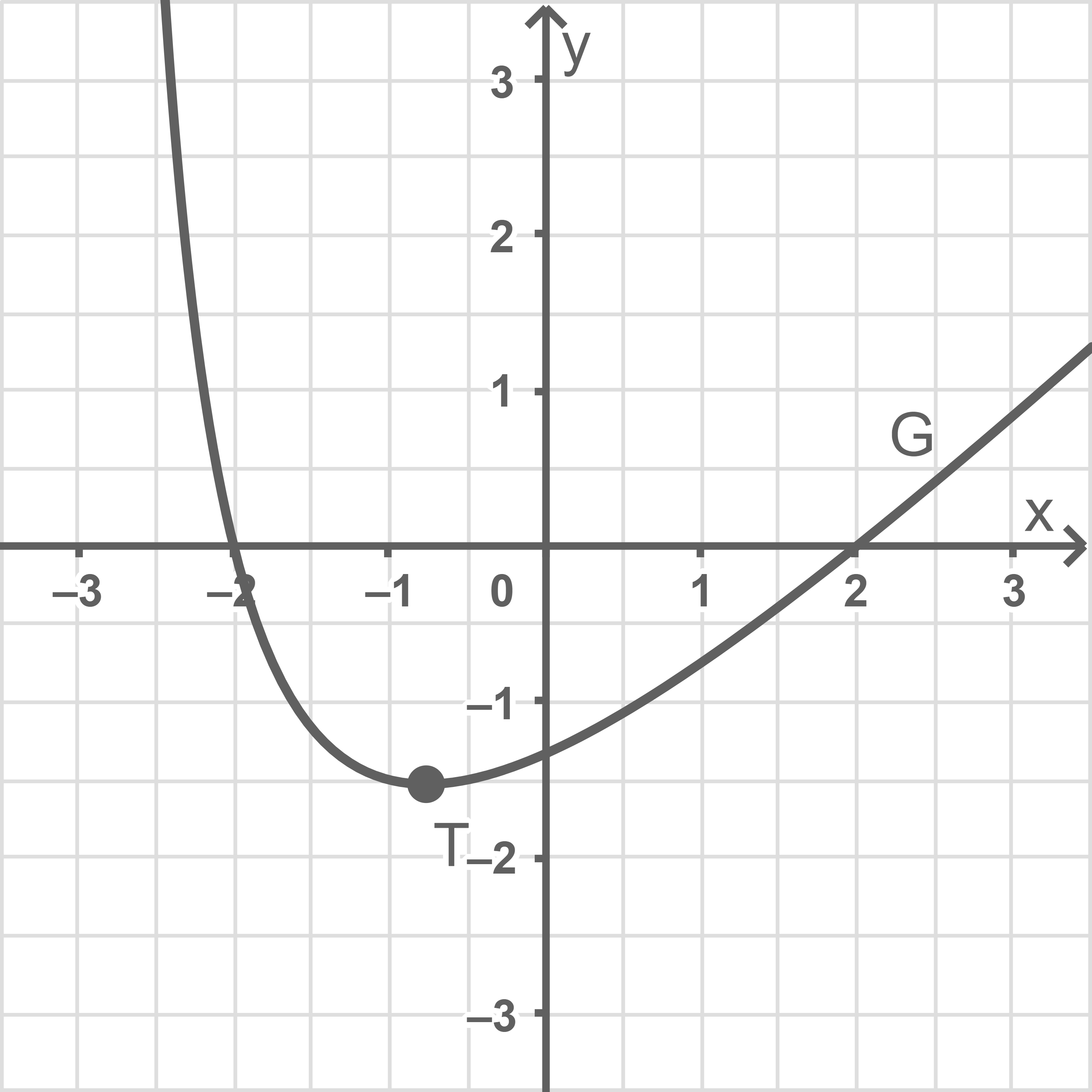
![\(]-3 ;+\infty[\)](https://mathjax.schullv.de/c0ec94a19df0d53232a4f1cded745498d679cb61dba6218b919425c41ac684d6?color=5a5a5a) definierte Integralfunktion
definierte Integralfunktion 

a)
Die Geraden mit den Gleichungen  und
und  haben eine besondere Bedeutung für
haben eine besondere Bedeutung für  Zeichne die beiden Geraden in die Abbildung ein und gib diese Bedeutung an. Gib zudem die Koordinaten des Schnittpunkts der beiden Geraden an.
Zeichne die beiden Geraden in die Abbildung ein und gib diese Bedeutung an. Gib zudem die Koordinaten des Schnittpunkts der beiden Geraden an.
(4 BE)
b)
Berechne die Koordinaten des Schnittpunkts von  mit der
mit der  -Achse. Begründe anhand des gegebenen Terms von
-Achse. Begründe anhand des gegebenen Terms von  dass
dass  für
für  oberhalb der Geraden mit der Gleichung
oberhalb der Geraden mit der Gleichung  verläuft.
verläuft.
(3 BE)
c)
Weise nach, dass  gilt, indem du den Term
gilt, indem du den Term  geeignet umformst, und begründe, dass
geeignet umformst, und begründe, dass  genau die Nullstellen
genau die Nullstellen  und
und  hat.
hat.
(3 BE)
d)
Ermittle rechnerisch einen Term der ersten Ableitungsfunktion  von
von  und berechne die
und berechne die  -Koordinate von
-Koordinate von 
(5 BE)
e)
Ermittle anhand der Abbildung einen Näherungswert für das Integral 
Betrachtet wird die in
(3 BE)
f)
Begründe, dass die in ![\(\left]-3;+\infty\right[\)](https://mathjax.schullv.de/cc0494289ca46edc6787a6fa9486baf09204545890f2e99e353d16142858c010?color=5a5a5a) definierte Funktion
definierte Funktion  für
für  eine Stammfunktion von
eine Stammfunktion von  ist. Zeige damit, dass
ist. Zeige damit, dass  gilt, und deute diese Aussage geometrisch.
gilt, und deute diese Aussage geometrisch.
(6 BE)
g)
Begründe ohne weitere Rechnung, dass  mindestens zwei Nullstellen besitzt.
mindestens zwei Nullstellen besitzt.
(3 BE)
2
Betrachtet wird die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet. Die Funktion
bezeichnet. Die Funktion  aus Aufgabe 1 ist somit die Funktion
aus Aufgabe 1 ist somit die Funktion  dieser Schar.
dieser Schar.
 gilt
gilt 
 im Punkt
im Punkt  wird mit
wird mit  bezeichnet.
bezeichnet.
a)
Gib die Anzahl der Nullstellen von  in Abhängigkeit von
in Abhängigkeit von  an und begründe, dass die Funktion
an und begründe, dass die Funktion  der Schar eine Nullstelle ohne Vorzeichenwechsel hat.
der Schar eine Nullstelle ohne Vorzeichenwechsel hat.
Für die erste Ableitungsfunktion von
(4 BE)
b)
Begründe, dass  für
für  keine Extrempunkte besitzt.
keine Extrempunkte besitzt.
Die Tangente an
(2 BE)
c)
Zeige, dass  die Steigung
die Steigung  hat, und bestimme denjenigen Wert von
hat, und bestimme denjenigen Wert von  für den
für den  senkrecht zur Gerade mit der Gleichung
senkrecht zur Gerade mit der Gleichung  ist.
ist.
(3 BE)
d)
Gib eine Gleichung von  an und beurteile folgende Aussage:
an und beurteile folgende Aussage:

Es gibt einen Punkt, der für alle  auf
auf  liegt.
liegt.
(4 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
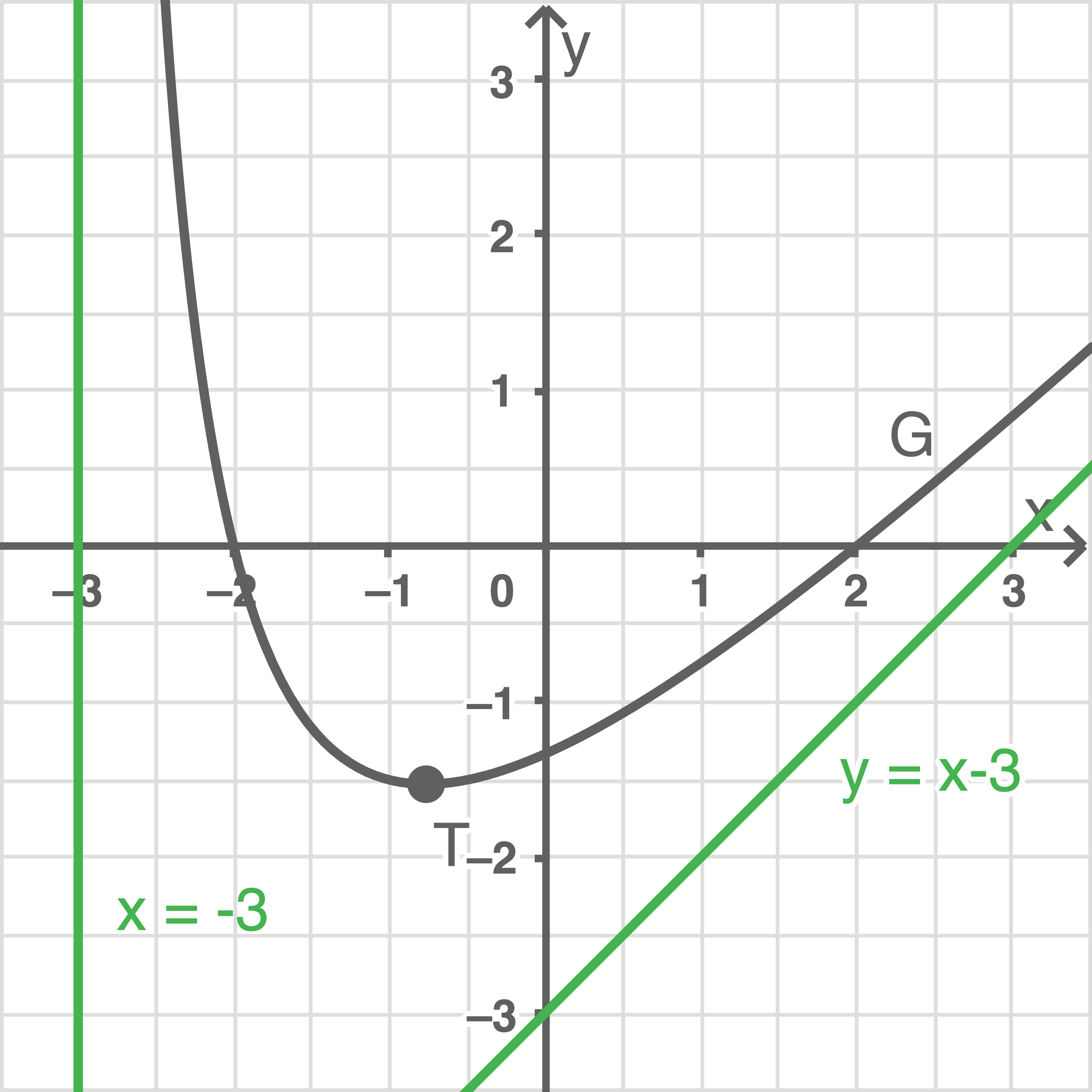
b)
Koordinaten berechnen
Einsetzen von  in den Funktionsterm liefert:
in den Funktionsterm liefert:
![\(\begin{array}[t]{rll}
f(0)&=&0 - 3 + \dfrac{5}{0 + 3} \\[5pt]
&=&-\dfrac{4}{3}
\end{array}\)](https://mathjax.schullv.de/fcc5e2bba9fde7796a9b8b6220e678d2909420b151e56c76cd9eef87c72a14e0?color=5a5a5a) Die Koordinaten des Schnittpunkts von
Die Koordinaten des Schnittpunkts von  mit der
mit der  -Achse sind somit gegeben durch
-Achse sind somit gegeben durch  Lage von
Lage von  begründen
Für
begründen
Für  ist der Ausdruck
ist der Ausdruck  positiv, das heißt es gilt
positiv, das heißt es gilt  Somit liegt
Somit liegt  für diese Werte von
für diese Werte von  oberhalb der Geraden
oberhalb der Geraden 
c)
Funktionsterm nachweisen
![\(\begin{array}[t]{rll}
f(x)&=&x-3+\dfrac{5}{x + 3} \\[5pt]
&=&\dfrac{(x - 3)\cdot(x + 3) + 5}{x + 3} \\[5pt]
&=&\dfrac{x^2 - 4}{x + 3}
\end{array}\)](https://mathjax.schullv.de/bc7794265a615241479a771ebb89c9e6a97cea06cac5dc1a0249871659af5b87?color=5a5a5a) Nullstellen begründen
Die Nullstellen von
Nullstellen begründen
Die Nullstellen von  ergeben sich aus den Nullstellen des Zählers von
ergeben sich aus den Nullstellen des Zählers von  somit folgt:
somit folgt:
![\(\begin{array}[t]{rll}
x^2 - 4&=&0 &\quad \scriptsize \mid\;+4 \\[5pt]
x^2&=&4 &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
x_{1;2}&=&\pm2
\end{array}\)](https://mathjax.schullv.de/6559c858970fb98999fe533433cdd622803697cf747c99ae52162206b16623de?color=5a5a5a)
d)
Ableitungsfunktion bestimmen
Mit der Quotientenregel folgt für den Funktionsterm der Ableitung von 
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/6daee4f834b3875413a8b64bbeea613b1e0ebc461f191f56e04280fed23f20b9?color=5a5a5a)
 -Koordinate von
-Koordinate von  berechnen
Anwenden der notwendigen Bedingung für Extremstellen liefert:
berechnen
Anwenden der notwendigen Bedingung für Extremstellen liefert:
![\(\begin{array}[t]{rll}
\dfrac{x^2+6x+4}{(x+3)^2}&=&0 &\quad \scriptsize \mid\;\cdot(x+3)^2\\[5pt]
x^2+6x+4&=&0
\end{array}\)](https://mathjax.schullv.de/d7f7fc138953a91e796ec429004781d1c82d1c1971625c551b5b8a62fed95cd1?color=5a5a5a) Mit der
Mit der  -Formel folgt weiter:
-Formel folgt weiter:
![\(\begin{array}[t]{rll}
x_{1;2}&=&\dfrac{-6\pm\sqrt{6^2-16}}{2} \\[5pt]
x_{1;2}&=&\dfrac{-6\pm\sqrt{20}}{2} \\[5pt]
x_1&=&\dfrac{-6+\sqrt{20}}{2} \\[5pt]
x_1&\approx&-0,76 \\[5pt]
x_2&=&\dfrac{-6-\sqrt{20}}{2} \\[5pt]
x_2&\approx&-5,23
\end{array}\)](https://mathjax.schullv.de/fc04f925276ed1db5ec6a152b7955f55ff95bef2359c1227f8e848e0ce73d299?color=5a5a5a) Mit Hilfe der Abbildung folgt somit, dass
Mit Hilfe der Abbildung folgt somit, dass  die
die  -Koordinate von
-Koordinate von  ist.
ist.
e)
Der Wert des Integrals ist durch den Inhalt der Fläche zwischen der  -Achse und dem Graphen zwischen
-Achse und dem Graphen zwischen  und
und  gegeben. Zählen der Kästchen ergibt ungefähr
gegeben. Zählen der Kästchen ergibt ungefähr  Kästchen. Da vier Kästchen einer Flächeneinheit entsprechen, folgt
Kästchen. Da vier Kästchen einer Flächeneinheit entsprechen, folgt  als Näherungswert des Integrals.
als Näherungswert des Integrals.
f)
Stammfunktion begründen
Ableiten von  liefert:
liefert:
![\(\begin{array}[t]{rll}
F](https://mathjax.schullv.de/f045f786addacd6ea18538504ed6fdf2008a88a5af629b8803d8f51fe57cddc3?color=5a5a5a) Somit ist
Somit ist  eine Stammfunktion von
eine Stammfunktion von  Grenzwert zeigen
Es gilt
Grenzwert zeigen
Es gilt  und damit auch
und damit auch  sowie
sowie  Aussage geometrisch deuten
Da
Aussage geometrisch deuten
Da  die Flächenbilanz von
die Flächenbilanz von  zwischen
zwischen  und
und  angibt, bedeutet
angibt, bedeutet  dass die Fläche unendlich groß wird, wenn
dass die Fläche unendlich groß wird, wenn  sich von rechts
sich von rechts  nähert.
nähert.
g)
Die Funktion  hat mindestens zwei Nullstellen, da
hat mindestens zwei Nullstellen, da  ist, sowie der Graph
ist, sowie der Graph  für
für  -Werte größer als
-Werte größer als  nach Aufgabenteil b) immer oberhalb der
nach Aufgabenteil b) immer oberhalb der  -Achse verläuft. Da
-Achse verläuft. Da  zwischen
zwischen  und
und  eine Fläche unterhalb der
eine Fläche unterhalb der  -Achse einschließt, existiert somit ein
-Achse einschließt, existiert somit ein  sodass die zwischen
sodass die zwischen  und
und  unterhalb der
unterhalb der  -Achse eingeschlossene Fläche der zwischen
-Achse eingeschlossene Fläche der zwischen  und
und  oberhalb der
oberhalb der  -Achse eingeschlossenen Fläche entspricht. Somit gilt dann
-Achse eingeschlossenen Fläche entspricht. Somit gilt dann 
2
a)
Anzahl der Nullstellen angeben
Die Nullstellen von  ergeben sich als die des Zählers
ergeben sich als die des Zählers  Für
Für  hat
hat  somit zwei Nullstellen, für
somit zwei Nullstellen, für  eine Nullstelle und für
eine Nullstelle und für  keine Nullstelle.
Nullstelle ohne Vorzeichenwechsel begründen
Für
keine Nullstelle.
Nullstelle ohne Vorzeichenwechsel begründen
Für  ist
ist  eine doppelte Nullstelle von
eine doppelte Nullstelle von  das heißt der Graph
das heißt der Graph  besitzt dort ein Extremum und berührt somit die
besitzt dort ein Extremum und berührt somit die  -Achse nur. Damit hat
-Achse nur. Damit hat  eine Nullstelle ohne Vorzeichenwechsel.
eine Nullstelle ohne Vorzeichenwechsel.
b)
Für  hat der Zähler
hat der Zähler  und damit auch
und damit auch  keine Nullstellen, da die Diskriminante
keine Nullstellen, da die Diskriminante  negativ ist. Somit besitzt
negativ ist. Somit besitzt  für
für  keine Extrempunkte.
keine Extrempunkte.
c)
Für die Steigung  der Tangente
der Tangente  an
an  bei
bei  gilt:
gilt:
 Die Tangente
Die Tangente  ist senkrecht zur Geraden
ist senkrecht zur Geraden  wenn das Produkt der Steigungen
wenn das Produkt der Steigungen  ergibt. Somit folgt für den gesuchten Wert von
ergibt. Somit folgt für den gesuchten Wert von 
![\(\begin{array}[t]{rll}
\dfrac{k}{9}\cdot1&=&-1 &\quad \scriptsize \mid\;\cdot9 \\[5pt]
k&=&-9
\end{array}\)](https://mathjax.schullv.de/9749dcfb3b87d97d3ac49dd668574bbfa3433dbebe882172e9eec80d8dd6e0db?color=5a5a5a)
d)
Für die Tangente  gilt
gilt  Da
Da  gilt, folgt:
gilt, folgt:
 Einsetzen von
Einsetzen von  in den Funktionsterm von
in den Funktionsterm von  liefert:
liefert:
![\(\begin{array}[t]{rll}
t_k(3)&=&\dfrac{k}{9}\cdot3-\dfrac{k}{3} \\[5pt]
&=&0
\end{array}\)](https://mathjax.schullv.de/c352df33521eb2414c2c5063f2431ffe1813bea199fd36a76a60c34eda37d16b?color=5a5a5a) Somit liegt der Punkt mit den Koordinaten
Somit liegt der Punkt mit den Koordinaten  für alle
für alle  auf
auf  die Aussage stimmt also.
die Aussage stimmt also.