Teil A

Gegeben ist die Funktion $f: x\mapsto \sqrt{3x-5}$ mit maximalem Definitionsbereich $D.$ Gib $D$ an und bestimme die Gleichung der Tangente an den Graphen von $f$ im Punkt $(3\mid f(3)).$

(6 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)= -x^3+9x^2-15x-25.$
Weise nach, dass $f$ folgende Eigenschaften besitzt:

$(1)$

Der Graph von $f$ besitzt an der Stelle $x=0$ die Steigung $-15.$

$(2)$

Der Graph von $f$ besitzt im Punkt $A\left(5\mid f(5)\right)$ die $x$ -Achse als Tangente.

$(3)$

Die Tangente $t$ an den Graphen der Funktion $f$ im Punkt $B\left(-1\mid f(-1) \right)$ kann durch die Gleichung $y=-36x-36$ beschrieben werden.

(5 BE)

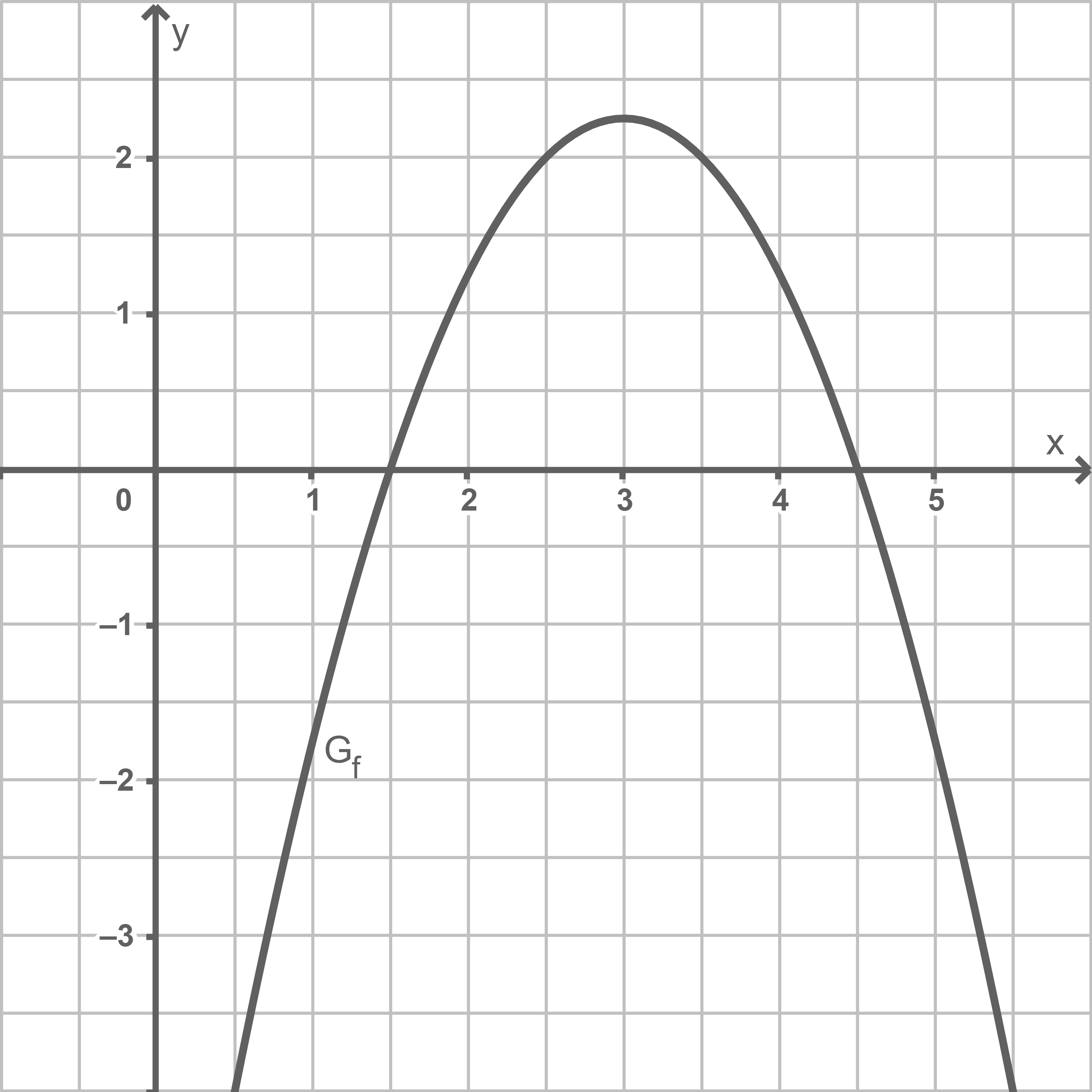
Die Abbildung zeigt eine nach unten geöffnete Parabel, die zu einer Funktion $f$ mit Definitionsbereich $\mathbb{R}$ gehört. Der Scheitel der Parabel hat die $x$ -Koordinate $3.$
Betrachtet wird die in $\mathbb{R}$ definierte Integralfunktion $F:x\mapsto \displaystyle\int_{3}^{x}f(t)\;\mathrm dt.$
Wie viele Nullstellen hat $F?$ Mache deine Antwort ohne Rechnung plausibel.

(4 BE)

Für jeden Wert von $a$ mit $a\in \mathbb{R}^+$ ist eine Funktion $f_a$ durch $f_a(x)=\frac{1}{a}\cdot x^3 -x$ mit $x\in \mathbb{R}$ gegeben.

Eine der beiden Abbildungen stellt einen Graphen von $f_a$ dar. Gib an, für welche Abbildung dies zutrifft. Begründe deine Antwort.

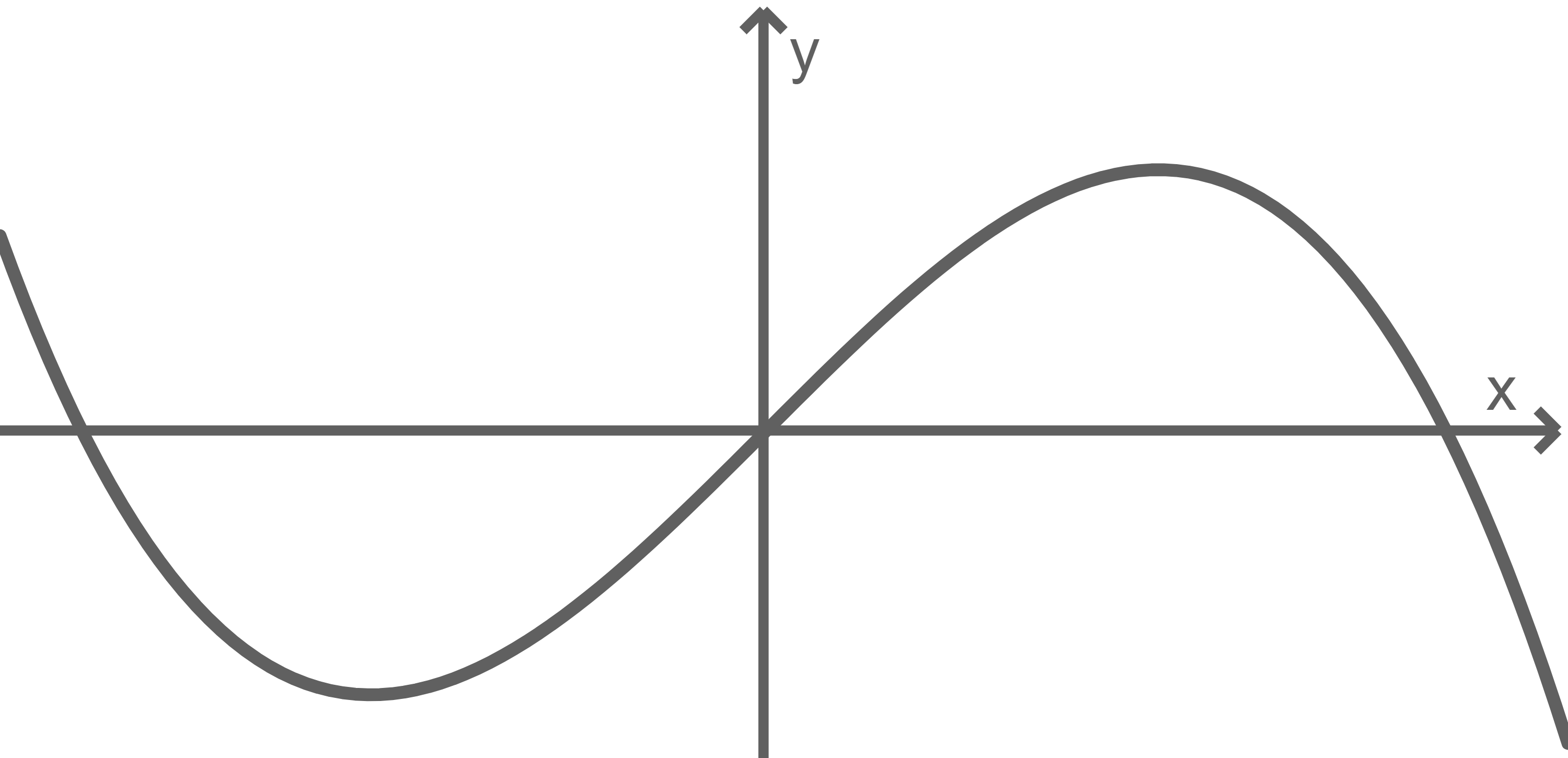
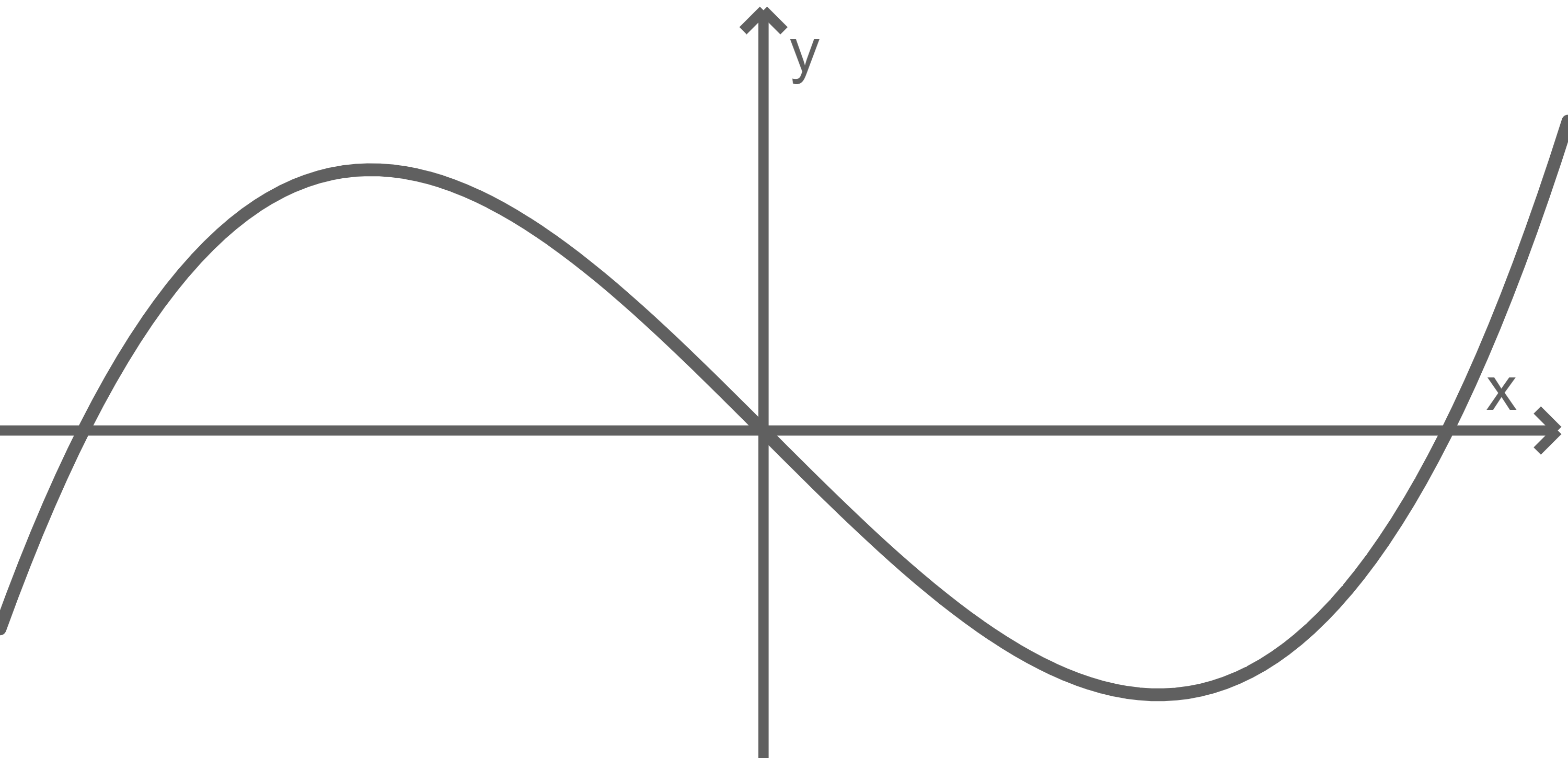
Abb. 1

Abb. 2

(2 BE)

Für jeden Wert von $a$ besitzt der Graph von $f_a$ genau zwei Extrempunkte. Ermittle denjenigen Wert von $a,$ für den der Graph der Funktion $f_a$ an der Stelle $x=3$ einen Extrempunkt hat.

(3 BE)

(20 BE)

Definitionsbereich angeben

Damit das Argument der Wurzel nicht negativ wird, ergibt sich für $x:$

$\begin{array}[t]{rll} 3x-5&\geq& 0 &\quad \scriptsize \mid\; +5 \\[5pt] 3x&\geq& 5 &\quad \scriptsize \mid\; :3 \\[5pt] x&\geq & \dfrac{5}{3} \end{array}$

Der maximale Definitionsbereich von $f$ ist somit gegeben durch $\mathbb{D} = \left[\frac{5}{3};+\infty\right[.$

Tangentengleichung bestimmen

Für die erste Ableitung von $f$ folgt mit Hilfe der Kettenregel:

$\( \begin{array}[t]{rll} f$

Einsetzen von $x=3$ in $f(x)$ und $\(f$ liefert:

$\begin{array}[t]{rll} f(3)&=& \sqrt{3\cdot 3 -5} \\[5pt] &=&\sqrt{4} \\[5pt] &=& 2 \end{array}$

$\(\begin{array}[t]{rll} f$

Die Steigung der Tangente $t:y= mx+b$ ist somit gegeben als $\( m= f$ Einsetzen der Koordinaten $(3\mid 2)$ liefert:

$\begin{array}[t]{rll} 2&=& \dfrac{3}{4}\cdot 3 + b \\[5pt] 2&=& \dfrac{9}{4} +b &\quad \scriptsize \mid\; -\frac{9}{4}\\[5pt] -\dfrac{1}{4}&=& b \end{array}$

Die Gleichung der Tangente an den Graphen von $f$ im Punkt $(3\mid f(3))$ ist somit durch $y= \frac{3}{4}x -\frac{1}{4}$ gegeben.

Ableiten von $f$ liefert:

$\(f$

$(1)$

Steigung

Einsetzen von $x=0$ in $\(f$ liefert:

$\(\begin{array}[t]{rll} f$

Der Graph von $f$ besitzt somit an der Stelle $x=0$ die Steigung $-15.$

$(2)$

Tangente

$\begin{array}[t]{rll} f(5)&=& -5^3+9\cdot 5^2 -15\cdot 5 -25 \\[5pt] &=& 0 \end{array}$

$\(\begin{array}[t]{rll} f$

Die $x$ -Achse mit der Gleichung $y= 0$ ist somit eine Tangente an den Graphen von $f$ im Punkt $A.$

$(3)$

Tangente

Die Gerade mit der Gleichung $y= -36x-36$ besitzt die Steigung $-36.$ Für die Steigung des Graphen von $f$ im Punkt $B$ gilt:

Rechenweg anzeigen

$\( f$

Für die Funktionswerte der beiden Funktionen an der Stelle $x=-1$ folgt:

$\begin{array}[t]{rll} y&=& -36\cdot (-1) -36 \\[5pt] &=& 0 \end{array}$

Rechenweg anzeigen

$f(-1)=0$

Da sowohl die beiden Steigungen, als auch die beiden Funktionswerte im Punkt $B$ übereinstimmen, kann die Tangente an den Graphen von $f$ im Punkt $B$ durch $y= -36x-36$ beschrieben werden.

Eine Nullstelle besitzt $F$ bei $x=3,$ da dort die untere mit der oberen Integrationsgrenze übereinstimmt.
Aus der Abbildung folgt, dass der Graph von $f$ bei $x_1 = 1,5$ und $x_2 = 4,5$ die $x$ -Achse schneidet. Da es sich um eine nach unten geöffnete Parabel handelt, liegt der Graph von $f$ für $x\lt 1,5$ und $x\gt 4,5$ unterhalb der $x$ -Achse.
Somit existieren aufgrund der Symmetrie zum Scheitelpunkt zwei Werte von $x,$ sodass der Graph von $f$ zwischen diesem Wert und der jeweiligen Nullstelle von $f$ eine Fläche unterhalb der $x$ -Achse einschließt, welche genau so groß ist wie der Inhalt der Fläche, die der Graph von $f$ mit der $x$ -Achse zwischen der Nulstelle und $x$ 03 überhalb der $x$ -Achse einschließt. Somit besitzt $F$ auch an diesen beiden Stellen eine Nullstelle.
Insgesamt besitzt die Funktion $F$ damit 3 Nullstellen.

Da $a$ eine positive reelle Zahl ist, folgt:

$\begin{array}[t]{rll} \lim\limits_{x\to +\infty}f_a(x)&=& \lim\limits_{x\to +\infty}\left(\frac{1}{a}\cdot x^3-x \right) \\[5pt] &=& +\infty \end{array}$

Somit stellt Abbildung 2 den Graph von $f_a$ dar.

Da die Ableitung von $f$ eine quadratische Funktion ist und somit maximal zwei Nullstellen besitzt, muss nur die notwendige Bedingung überprüft werden. Für die Ableitung von $f$ gilt:

$\(f_a$

Einsetzen von $x=3$ liefert:

$\(\begin{array}[t]{rll} f_a$

Für $a=27$ besitzt der Graph von $f_a$ an der Stelle $x=3$ somit einen Extrempunkt.