Teil B

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f:x \mapsto \mathrm{e}^{\frac{1}{2}x} + \mathrm{e}^{-\frac{1}{2}x}$ . Der Graph von $f$ wird mit $G_f$ bezeichnet.

Bestimme die Koordinaten des Schnittpunkts von $G_f$ mit der $y$ -Achse und begründe, dass $G_f$ oberhalb der $x$ -Achse verläuft.

(2 BE)

Ermittle das Symmetrieverhalten von $G_f$ sowie das Verhalten von $f$ für $x \mapsto -\infty$ und für $x \mapsto +\infty$ .

(3 BE)

Zeige, dass für die zweite Ableitung $f‘‘$ von $f$ die Beziehung $f‘‘(x)=\frac{1}{4}\cdot f(x)$ für $x\in\mathbb{R}$ gilt. Weise nach, dass $G_f$ linksgekrümmt ist.

(zur Kontrolle: $f‘(x)=\frac{1}{2}\cdot \left(\mathrm{e}^{\frac{1}{2}x} - \mathrm{e}^{-\frac{1}{2}x}\right)$ )

(4 BE)

Bestimme Lage und Art des Extrempunkts von $G_f$ .

(3 BE)

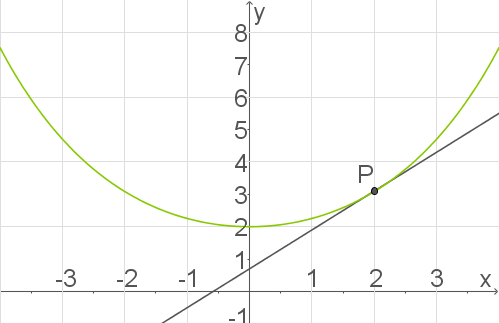
Berechne die Steigung der Tangente $g$ an $G_f$ im Punkt $P(2\mid f(2))$ auf eine Dezimale genau. Zeichne den Punkt $P$ und die Gerade $g$ in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: $-4\leq x\leq 4,\, -1\leq y \leq 9$ ).

(3 BE)

Berechne $f(4)$ , im Hinblick auf eine der folgenden Aufgaben auf zwei Dezimalen genau, und zeichne unter Berücksichtigung der bisherigen Ergebnisse $G_f$ im Bereich $-4\leq x\leq 4$ in das Koordinatensystem aus Aufgabe 1e ein.

(4 BE)

Zeige durch Rechnung, dass für $x\in\mathbb{R}$ die Beziehung $\frac{1}{4}\cdot [f(x)]^2-[f‘(x)]^2=1$ gilt.

(3 BE)

Die als Kurvenlänge $L_{a;b}$ bezeichnete Länge des Funktionsgraphen von $f$ zwischen den Punkten $(a\mid f(a))$ und $(b\mid f(b))$ mit $a\lt b$ lässt sich mithilfe der Formel $L_{a;b}=\displaystyle\int_{a}^{b}\sqrt{1+[f‘(x)]^2} \;\mathrm dx$ berechnen.

Bestimme mithilfe der Beziehung aus Aufgabe 1 g) die Kurvenlänge $L_{0;b}$ des Graphen von $f$ zwischen den Punkten $(0\mid f(0))$ und $(b \mid f (b))$ mit $b\gt 0$ .

(Ergebnis: $L_{0;b}= \mathrm{e}^{\frac{1}{2}b} - \mathrm{e}^{-\frac{1}{2}b}$ )

(4 BE)

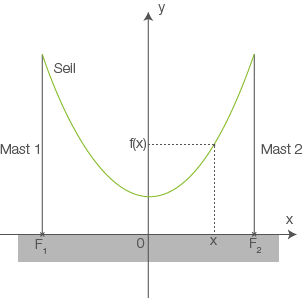
Die Enden eines Seils werden an zwei vertikalen Masten, die $8,00\,\text{m}$ voneinander entfernt sind, in gleicher Höhe über dem Erdboden befestigt. Der Graph $G_f$ aus Aufgabe 1 beschreibt im Bereich $-4\leq x\leq 4$ modellhaft den Verlauf des Seils, wobei die Fußpunkte $F_1$ und $F_2$ der Masten durch die Punkte $(-4\mid 0)$ bzw. $(4\mid 0)$ dargestellt werden (vgl. Abbildung). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.

Diagramm einer Parabel mit Achsenbeschriftungen und Punkten für Sell, Mast 1 und Mast 2.

Abb. 1

Der Höhenunterschied zwischen den Aufhängepunkten und dem tiefsten Punkt des Seils wird als Durchhang bezeichnet. Berechne auf der Grundlage des Modells den Durchhang des Seils auf Zentimeter genau.

(2 BE)

Berechne auf der Grundlage des Modells die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, sowie mithilfe der Kurvenlänge aus Aufgabe 1 h) die Länge des zwischen den Masten hängenden Seils auf Zentimeter genau.

(5 BE)

Der Graph von $f$ soll durch eine Parabel näherungsweise dargestellt werden. Dazu wird die in $\mathbb{R}$ definierte quadratische Funktion $q$ betrachtet, deren Graph den Scheitelpunkt $(0\mid 2)$ hat und durch den Punkt $(4\mid f(4))$ verläuft.

Ermittle den Term $q(x)$ der Funktion $q$ , ohne dabei zu runden.

(4 BE)

Für jedes $x\in ]0;4 [$ wird der Abstand der vertikal übereinander liegenden Punkte $(x\mid q(x))$ und $(x\mid f(x))$ der Graphen von $q$ bzw. $f$ betrachtet, wobei in diesem Bereich $q(x)\gt f(x)$ gilt. Der größte dieser Abstände ist ein Maß dafür, wie gut die Parabel den Graphen $G_f$ im Bereich $0\lt x\lt 4$ annähert. Beschreibe die wesentlichen Schritte, mithilfe derer man diesen größten Abstand rechnerisch bestimmen kann.

(3 BE)

(40 BE)

Bildnachweise [nach oben]

[1]

$\blacktriangleright$ Koordinaten des Schnittpunkts mit der $\boldsymbol{y}$ -Achse bestimmen

Du sollst den Schnittpunkt des Graphen $G_f$ der Funktion $f:\, x\mapsto e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}$ mit der $y$ -Achse bestimmen. Berechne also $f(0):$

$\begin{array}[t]{rll} f(0)&=& e^{\frac{1}{2}\cdot 0}+e^{-\frac{1}{2}\cdot 0} \\[5pt] &=& 2\cdot e^0 &\quad \scriptsize \mid\; e^0=1 \\[5pt] &=& 2 \end{array}$

$G_f$ schneidet die $y$ -Achse im Punkt $(0\vert 2)$ .

$\blacktriangleright$ Lage des Graphen begründen

Du sollst begründen, dass $G_f$ immer oberhalb der $x$ -Achse verläuft. Dazu betrachtest du die Funktionsvorschrift von $f$ und erkennst, dass sie aus einer Addition von zwei $\mathrm e$ -Funktionen besteht.

$\mathrm e$ -Funktionen sind für alle Argumente strikt positiv und somit ist die Summe zweier ebenfalls immer größer als $0$ . Damit verläuft der Graph immer oberhalb der $x$ -Achse.

$\blacktriangleright$ Symmetrieverhalten von $\boldsymbol{G_f}$ ermitteln

Du sollst $G_f$ auf Punkt- oder Achsensymmetrie untersuchen. Dazu betrachtest du $f(-x)$ und überprüfst, ob du die Gleichung zu

$f(x)$ für Achsensymmetrie zur $y$ -Achse oder
$-f(x)$ für Punktsymmetrie zum Koordinatenursprung

umformen kannst. Berechne zuerst $f(-x)$ :

$\begin{array}[t]{rll} f(-x)&=& e^{\frac{1}{2}\cdot (-x)}+e^{-\frac{1}{2}\cdot (-x)} \\[5pt] &=& e^{-\frac{1}{2}\cdot x}+e^{\frac{1}{2}\cdot x} \\[5pt] &=& e^{\frac{1}{2}\cdot x}+e^{-\frac{1}{2}\cdot x} \\[5pt] &=& f(x) \end{array}$

Somit ist $G_f$ achsensymmetrisch zur $y$ -Achse. Da es sich nicht um eine konstante Gerade handelt, kann $G_f$ nicht zusätzlich punktsymmetrisch sein.

$\blacktriangleright$ Grenzverhalten untersuchen

Oben hast du bereits gezeigt, dass der Graph von $f$ achsensymmetrisch zur $y$ -Achse ist. Das bedeutet auch, dass das Verhalten von $f$ für $x \to -\infty$ und für $x\to \infty$ gleich ist. Du musst also nur eines von beiden genauer untersuchen. Bilde dazu den Grenzwert $\lim\limits_{x\to\infty}f(x)$ :

$\begin{array}[t]{rll} \lim\limits_{x\to\infty}f(x) &=& \lim\limits_{x\to\infty}\left( e^{\frac{1}{2}x}+e^{-\frac{1}{2}x} \right) \\[5pt] &=& \infty +0 \\[5pt] &=& \infty \\[5pt] \end{array}$

Für $x\to -\infty$ und $x\to \infty$ gilt also $f(x) \to \infty$ .

$\blacktriangleright$ Zweite Ableitungsfunktion nachweisen

Du sollst nachweisen, dass für die zweite Ableitungsfunktion $f‘‘(x)=\frac{1}{4}\cdot f(x)$ gilt. Bilde also die ersten beiden Ableitungsfunktionen von $f:$

$\begin{array}[t]{rll} f(x)&=& e^{\frac{1}{2}x}+e^{-\frac{1}{2}x} \\[10pt] f‘(x)&=& \frac{1}{2} \cdot e^{\frac{1}{2}x} - \frac{1}{2} \cdot e^{-\frac{1}{2}x} \\[5pt] &=& \frac{1}{2}\cdot\left(e^{\frac{1}{2}x}-e^{-\frac{1}{2}x}\right) \\[10pt] f‘‘(x)&=& \frac{1}{2}\cdot\left( \frac{1}{2} \cdot e^{\frac{1}{2}x} -\left(- \frac{1}{2} \cdot e^{-\frac{1}{2}x} \right)\right) \\[5pt] &=& \frac{1}{2}\cdot\left( \frac{1}{2} \cdot e^{\frac{1}{2}x} + \frac{1}{2} \cdot e^{-\frac{1}{2}x} \right) \\[5pt] &=& \frac{1}{4}\cdot \left(e^{\frac{1}{2}x}+e^{-\frac{1}{2}x}\right) \\[5pt] &=& \frac{1}{4}\cdot f(x) \end{array}$

Die Forderung der Aufgabenstellung ist erfüllt.

$\blacktriangleright$ Linkskrümmung nachweisen

Du sollst die Linkskrümmung von $G_f$ nachweisen. Der Graph einer Funktion $f$ ist linksgekrümmt, wenn $f(x) \gt 0$ ist. Für die zweite Ableitung hast du gerade $f‘‘(x)=\frac{1}{4}\cdot f(x)$ bestimmt.

Aus Teilaufgabe a) weißt du, dass $f(x)$ immer größer als $0$ ist, somit ist auch $\frac{1}{4}\cdot f(x)$ und damit $f‘‘(x)$ immer größer als $0$ und $G_f$ daher linksgekrümmt für alle $x$ aus dem Definitionsbereich.

$\blacktriangleright$ Lage und Art des Extrempunkts bestimmen

Du hast die Funktion $f$ gegeben und sollst deren Graph auf Extrempunkte untersuchen. Für eine Extremstelle $x_E$ benötigst du die beiden folgenden Kriterien:

Notwendiges Kriterium: $\, f‘(x_E)=0$
Hinreichendes Kriterium:
- Ist $f‘‘(x_E)\gt 0$ , handelt es sich um eine Minimalstelle.
- Ist $f‘‘(x_E)\lt 0$ , handelt es sich um eine Maximalstelle.

Du kannst also wie folgt vorgehen:

Wende das notwendige Kriterium an, indem du $f‘(x)=0$ setzt und nach $x$ löst.
Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in $f‘‘(x)$ einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
Berechne die Funktionswerte von $f$ an den Extremstellen.

1. Schritt: Notwendiges Kriterium anwenden

Durch Gleichsetzen von $f‘(x)$ mit Null, erhältst du mögliche Extremstellen:

$\begin{array}[t]{rll} f‘(x)&=& 0 \\[5pt] x_E&=& 0 \\[5pt] \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Hinreichendes Kriterium überprüfen

Um auf die Art des Extremums zu schließen, setzt du $x_E$ in $f‘‘(x)$ ein:

$\begin{array}[t]{rll} f‘‘(0)&=& \frac{1}{4}\cdot \left(e^{\frac{1}{2}\cdot 0}+e^{-\frac{1}{2}\cdot 0}\right) \\[5pt] &=& \frac{1}{4}\cdot \left(2\cdot e^0\right) \\[5pt] &=& \frac{1}{2} \cdot 1 \\[5pt] &=& \frac{1}{2} \gt 0 \end{array}$

Bei der Extremstelle $x_E=0$ handelt es sich um eine Minimalstelle.

3. Schritt: Funktionswerte berechnen

Um auch die $y$ -Koordinate des Tiefpunkts zu bestimmen, berechnest du den zugehörigen Funktionswert, welchen du bereits in Teilaufgabe a) bestimmt hast.

$G_f$ besitzt genau einen Extrempunkt. Dabei handelt es sich um einen Tiefpunkt mit den Koordinaten $T(0\mid 2).$

$\blacktriangleright$ Steigung der Tangenten im Punkt $\boldsymbol{P\,(2\vert f(2))}$ bestimmen

Du sollst die Steigung der Tangente an den Graphen von $f$ an der Stelle $x=2$ bestimmen. Die Steigung einer Tangente an einen Graphen hat immer die gleiche Steigung wie der Graph der Funktion im Berührpunkt. Da die Steigung eines Graphen durch die erste Ableitungsfunktion beschrieben wird, ist also $f‘(2)$ gesucht.

$\begin{array}[t]{rll} f‘(2)&=& \frac{1}{2}\cdot\left(e^{\frac{1}{2}\cdot 2}-e^{-\frac{1}{2}\cdot 2}\right) \\[5pt] &=& \frac{1}{2}\cdot \left(e^1-e^{-1}\right) \\[5pt] &\approx & 1,2 \\[10pt] \end{array}$

Die Steigung der Tangente $g$ an $G_f$ im Punkt $P(2\mid f(2))$ beträgt ca. $1,2.$

$\blacktriangleright$ Punkt und Tangente in ein Koordinatensystem einzeichnen

Es gilt:

$\begin{array}[t]{rll} f(2)&=&\mathrm e^{\frac{1}{2}\cdot 2}+ \mathrm e^{-\frac{1}{2}\cdot 2} \\[5pt] &=& \mathrm e+\mathrm e^{-1} \\[5pt] &\approx& 3,1 \end{array}$

Zeichnest du nun zuerst das Koordinatensystem im angegebenen Bereich und trägst den Punkt $P$ ein, kannst du die Tangente mit Hilfe der Steigung durch den Punkt $P$ legen.

Graph mit x- und y-Achse, einer Linie und dem Punkt P.

Abb. 1: Tangente und Punkt im Koordinatensystem

$\blacktriangleright$ Funktionswert berechnen

Du sollst den Funktionswert an der Stelle $x=4$ berechnen, setze dazu $4$ in $f(x)$ ein.

$\begin{array}[t]{rll} f(4)&=& e^{\frac{1}{2}\cdot 4}+e^{-\frac{1}{2}\cdot 4} \\[5pt] &=& e^2+e{^-2} \\[5pt] &\approx& 7,52 \end{array}$

An der Stelle $x=4$ beträgt der Funktionswert ungefähr $7,52$ . Im Koordinatensystem aus Teilaufgabe e) ergibt sich:

Graph einer Parabel mit einer tangentialen Linie, die den Punkt P berührt. Achsen sind beschriftet.

Abb. 2: $G_f$ im Koordinatensystem von Teilaufgabe e)

$\blacktriangleright$ Äquivalenz zeigen

Du sollst zeigen, dass für alle $x$ aus $\mathbb{R}$ gilt:

$\frac{1}{4}\cdot \left[f(x) \right]^2-\left[f‘(x) \right]^2 = ...$

Vollständige Lösung anzeigen

Damit hast du gezeigt, dass für alle $x$ die Gleichheit erfüllt ist.

$\blacktriangleright$ Kurvenlänge berechnen

Du sollst die Kurvenlänge $L_{0;b}$ zwischen den Punkten $(0\vert f(0))$ und $(b\vert f(b))$ mit $b\gt 0$ berechnen. Dazu verwendest du die Formel:

$L_{0;b}=\int\limits_{0}^{b}\sqrt{1+\left[f‘(x)\right]^2}\; dx$

Du erhältst:

L_{0;b} = \mathrm e^{\frac{1}{2}b}-\mathrm e^{-\frac{1}{2}b}

Vollständige Lösung anzeigen

Die Kurvenlänge zwischen $(0\vert 2)$ und $(b\vert f(b))$ beträgt $e^{\frac{1}{2}b}-e^{-\frac{1}{2}b}$ .

$\blacktriangleright$ Durchhang berechnen

Du sollst den Durchhang des Seiles berechnen. Der Verlauf des Seils wird modellhaft durch den Graphen $G_f$ beschrieben, der tiefste Punkt des Seils also durch den Tiefpunkt von $G_f$ und die Aufhängepunkte durch $Q(-4\mid f(-4))$ und $R(4\mid f(4)).$
Die zugehörige Höhe ergibt sich über den jeweiligen Funktionswert. Du erhältst:

$\begin{array}[t]{rll} D&=& f(4)-f(0) \\[5pt] &\approx & 7,52-2 \\[5pt] &=& 5,52 \end{array}$

Im Modell beträgt der Durchhang ca. $5,52\,$ m.

$\blacktriangleright$ Winkel zwischen Mast und Seil berechnen

Gesucht ist die Größe des Winkels $\beta$ (siehe Skizze). Diese kann über die Winkelsumme des eingezeichneten Dreiecks berechnet werden. Der Winkel $\alpha$ kann dazu als Steigungswinkel der Tangente $t$ an den Graphen von $f$ im Punkt $R(4\mid f(4))$ aufgefasst werden.
Die Größe von $\alpha$ kann entsprechend mithilfe der Steigung des Graphen von $f$ im Punkt $R,$ also $f‘(4)$ berechnet werden:

Es ist:

$\begin{array}[t]{rll} f‘(4)&=& \frac{1}{2}\cdot \left(\mathrm e^{\frac{1}{2}\cdot 4}-\mathrm e^{-\frac{1}{2}\cdot 4} \right) \\[5pt] &=& \frac{1}{2}\cdot \left(\mathrm e^{2}-\mathrm e^{-2} \right) \\[5pt] \end{array}$

Grafik einer Parabel mit Achsen und Beschriftungen zu Mast 1 und Mast 2 sowie Punkten P und f(x).

Abb. 3: Skizze

$\begin{array}[t]{rll} \alpha&=& \tan^{-1}\left( f‘(4) \right) \\[5pt] &=& \tan^{-1}\left(\frac{1}{2}\cdot\left(e^2-e^{-2} \right)\right) \\[5pt] &\approx & 74,59^{\circ} \end{array}$

Für $\beta$ gilt daher:

$\begin{array}[t]{rll} \beta&=& 180^{\circ}-90^{\circ}-74,59^{\circ} \\[5pt] &=& 15,41^{\circ} \end{array}$

Seil und Mast schließen einen Winkel von ungefähr $15,41^{\circ}$ ein.

$\blacktriangleright$ Länge des Seils zwischen den Masten

Du sollst die Länge des Seiles zwischen den Masten berechnen. In Aufgabe 1 h) hast du bereits die Kurvenlänge des Graphen von $f$ zwischen den Stellen $x=0$ und $x=b$ berechnet. Jetzt verwendest du, dass $G_f$ symmetrisch ist und berechnest die Kurvenlänge zwischen $0$ und $4$ und multiplizierst diese mit $2$ .

$\begin{array}[t]{rll} L_{-4;4}&=& 2\cdot L_{0;4} \\[5pt] &=& 2\cdot \left(e^{4\cdot \frac{1}{2}}-e^{-4\cdot \frac{1}{2}}\right) \\[5pt] &=& 2\cdot \left(e^{2}-e^{-2}\right) \\[5pt] &\approx& 14,51 \end{array}$

Die Länge des Seils beträgt ca. $14,51\,\text{m}$ .

$\blacktriangleright$ Term der quadratischen Gleichung bestimmen

Du sollst den Term der quadratischen Funktion bestimmen, deren Graph $G_f$ ideal annähert. Dazu betrachtst du die quadratische Gleichung in der Scheitelpunktform. Besitzt eine Parabel den Scheitelpunkt $S(x_S\mid y_S)$ , gilt für die Funktionsgleichung:

$\begin{array}[t]{rll} q(x)&=&a\cdot (x-x_S)^2+y_S \\[5pt] \end{array}$

Setze also die Koordinaten des Scheitelpunkts ein:

$q(x)= a\cdot \left(x- 0 \right)^2 +2 = ax^2+2$

Um $a$ zu bestimmen verwende die Koordinaten des zweiten vorgegebenen Punkts $(4\mid f(4))$ :

$\begin{array}[t]{rll} f(4)&=& q(4) \\[5pt] \mathrm e^{\frac{1}{2}\cdot 4}+\mathrm e^{-\frac{1}{2}\cdot 4}&=& a\cdot 4^2+2 \\[5pt] \mathrm e^{2}+\mathrm e^{-2}&=& a\cdot 16 +2 &\quad \scriptsize \mid\; -2\\[5pt] \mathrm e^{2}+\mathrm e^{-2} -2&=& a\cdot 16 &\quad \scriptsize \mid\; :16 \\[5pt] \dfrac{\mathrm e^{2}+\mathrm e^{-2} -2}{16}&=& a \end{array}$

Als Näherung erhältst du die quadratische Gleichung $q(x)=\dfrac{\mathrm e^{2}+\mathrm e^{-2} -2}{16}\cdot x^2+2$ . Beachte, dass du nicht runden sollst.

$\blacktriangleright$ Bestimmung des größten Abstandes beschreiben

Du sollst beschreiben wie der größte Abstand zwischen der Näherung und der Realität bestimmt werden kann.

Es ist dementsprechend das Maximum der Abstandsfunktion $d(x)=\left|g(x)-f(x)\right|$ gesucht.

Zunächst muss die Ableitung von $d(x)$ gebildet und auf Nullstellen untersucht werden, um das notwendige Kriterium für Extremstellen anzuwenden.

$\begin{array}[t]{rll} d‘(x)&=& 0 \\[5pt] \end{array}$

Von diesen Nullstellen wird die Art des Extremums durch Einsetzen in die zweite Ableitungsfunktion geprüft.

Den maximalen Abstand an sich erhält man durch Einsetzen der Maximalstellen in $d(x)$ .

Bildnachweise [nach oben]

[1]-[3]