Teil B

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_{a,b}: x\mapsto 1+a\cdot\mathrm{e}^{-bx}$ mit $a,b \in\mathbb{R^+}.$

Zeige, dass jede der Funktionen $f_{a,b}$ streng monoton abnehmend ist. Begründe, dass die Gerade mit der Gleichung $y=1$ für jede der Funktionen $f_{a,b}$ eine waagrechte Asymptote ihres Graphen ist.

(3 BE)

Der Graph einer der Funktionen der Schar enthält die Punkte $(1 \mid 2)$ und $(2 \mid 1,5)$ . Bestimme die zugehörigen Werte von $a$ und $b.$
Begründe ohne weitere Rechnung, dass die Schar keine Funktion umfasst, deren Graph die Punkte $(1 \mid 2)$ und $(4 \mid 0,5)$ enthält.

(4 BE)

Betrachtet wird nun die in $\mathbb{R}$ definierte Funktion $f: x \mapsto 1+7e^{-0,2x}$ , die eine der Funktionen der Schar aus Aufgabe 1 ist. Die Abbildung 1 zeigt ihren Graphen $G_f$ .

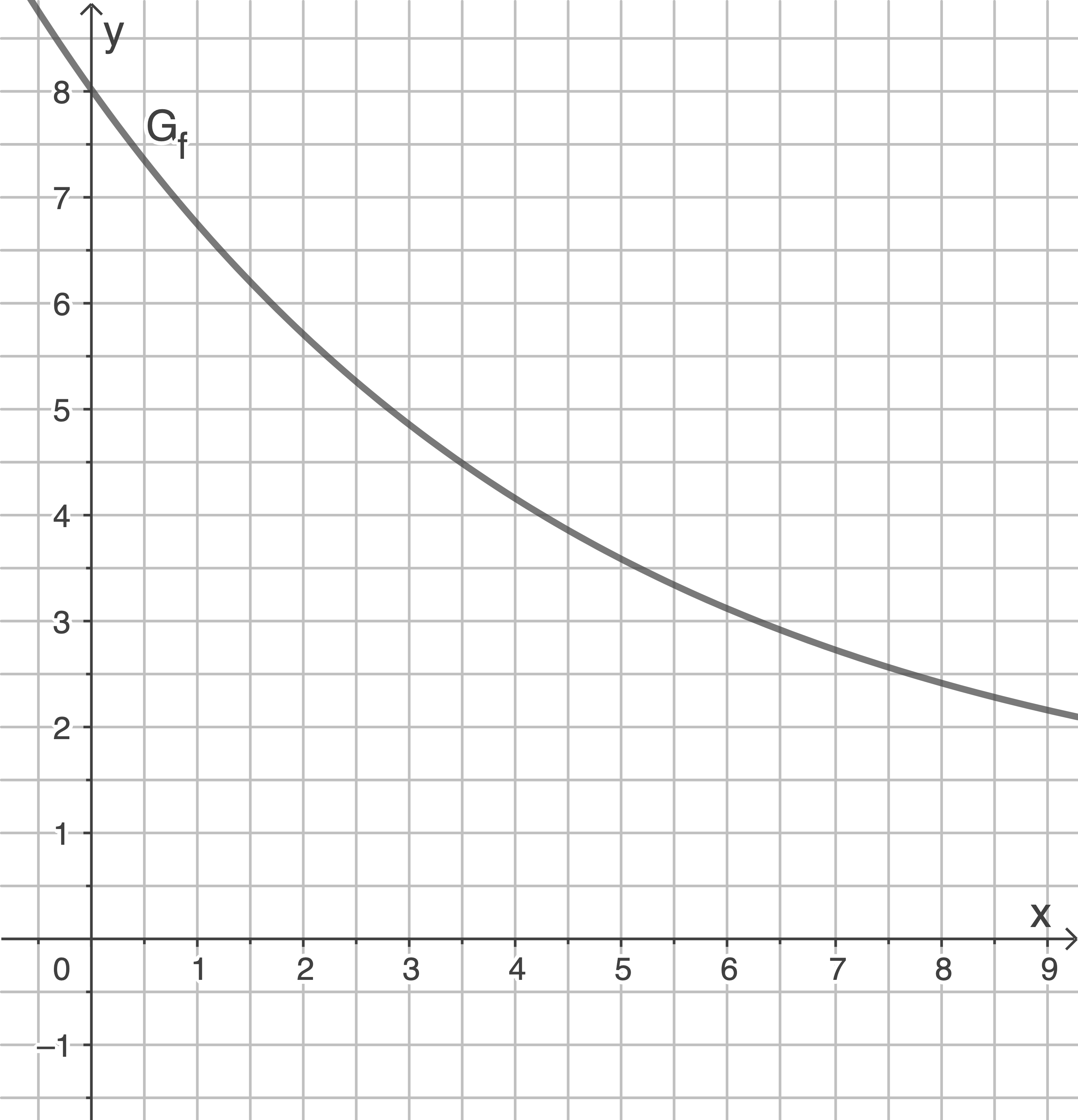
Graph einer Funktion mit Achsenbeschriftungen und einer abnehmenden Kurve.

Abb. 1

Beschreibe, wie $G_f$ aus dem Graphen der in $\mathbb{R}$ definierten natürlichen Exponentialfunktion $x \mapsto e^x$ hervorgeht.

Für jeden Wert $s \gt 0$ legen die Punkte $(0 \mid 1),$ $(s\mid 1),$ $(s \mid f(s))$ und $(0\mid f(s))$ ein Rechteck mit dem Flächeninhalt $R(s)$ fest.

(4 BE)

Zeichne dieses Rechteck für $s=5$ in die Abbildung 1 ein.
Zeige, dass $R(s)$ für einen bestimmten Wert von $s$ maximal ist, und gib diesen Wert von $s$ sowie den Flächeninhalt des zugehörigen Rechtecks an.

$\big[$ Zur Kontrolle: $R(s)= 7s \cdot \mathrm{e}^{-0,2 s}\big]$

(5 BE)

Bestimme in Abhängigkeit von $s$ $(s \gt 0)$ den Inhalt des Flächenstücks, das von $G_f$ , der $y$ -Achse sowie den Geraden mit den Gleichungen $y=1$ und $x=s$ begrenzt wird.
Einen Teil dieses Flächenstücks nimmt das oben beschriebene Rechteck mit dem Flächeninhalt $R(s)$ ein. Bestimme rechnerisch einen Näherungswert für $s$ so, dass der prozentuale Anteil des Flächeninhalts dieses Rechtecks am Inhalt des Flächenstücks $50\,\%$ beträgt.

(5 BE)

Die in $\mathbb{R}^+_0$ definierte Funktion $A: x\mapsto \frac{8}{f(x)}$ beschreibt modellhaft die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Südufer eines Sees. Dabei ist $x$ die seit Beobachtungsbeginn vergangene Zeit in Tagen und $A(x)$ der Flächeninhalt in Quadratmetern.

Gib $A(0)$ und $\lim\limits_{x\to +\infty}$ $A(x)$ sowie die jeweilige Bedeutung des Ergebnisses im Sachzusammenhang an. Begründe mithilfe des Monotonieverhaltens der Funktion $f$ , dass der Flächeninhalt des Algenteppichs im Laufe der Zeit ständig zunimmt.

(5 BE)

Die Funktion $A$ ist umkehrbar. Gib zur Umkehrfunktion von $A$ den Funktionsterm, die Definitionsmenge und die Wertemenge an. Beschreibe die Bedeutung der Umkehrfunktion von $A$ im Sachzusammenhang.

(5 BE)

Gib die momentane Änderungsrate des Flächeninhaltes des Algenteppichs zu Beobachtungsbeginn an.
Nur zu einem bestimmten Zeitpunkt, der im Modell mit $x_0$ bezeichnet wird, nimmt die momentane Änderungsrate des Flächeninhaltes des Algenteppichs ihren größten Wert an. Gib eine besondere Eigenschaft des Graphen von $A$ im Punkt $(x_0 \mid A(x_0))$ an, die sich daraus folgern lässt, und begründe deine Angabe.

(3 BE)

Zeichne den Graphen der Funktion $A$ unter Verwendung der bisherigen Ergebnisse in die Abbildung 2 ein.

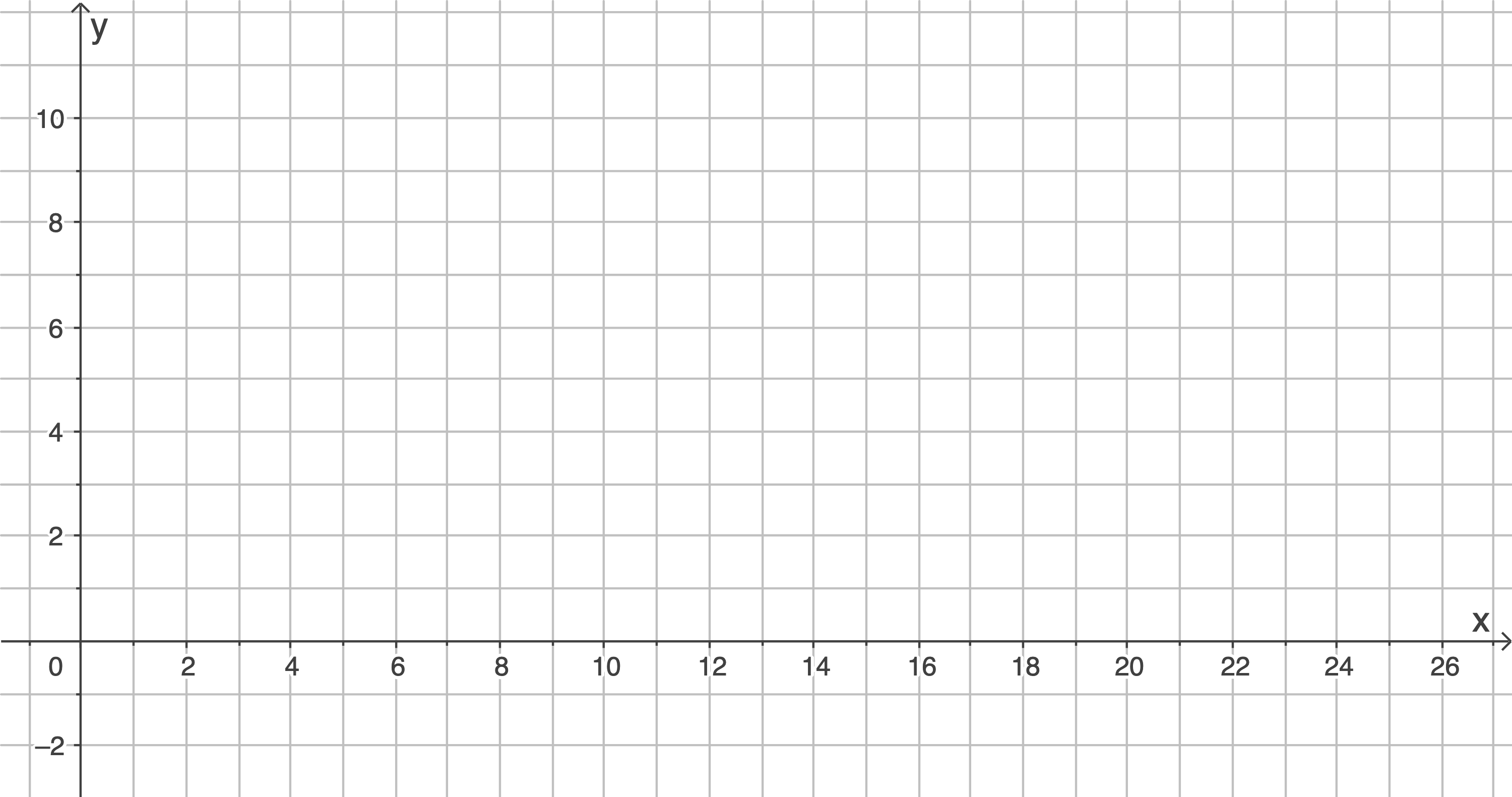
Leeres Koordinatensystem mit X- und Y-Achse, grauem Gitter und Zahlen von 0 bis 26 auf der X-Achse und 0 bis 10 auf der Y-Achse.

Abb. 2

(2 BE)

Um die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Nordufer des Sees zu beschreiben, wird im Term $A(x)$ die im Exponenten zur Basis $e$ enthaltene Zahl $-0,2$ durch eine kleinere Zahl ersetzt.
Vergleiche den Algenteppich am Nordufer mit dem am Südufer

hinsichtlich der durch $A(0)$ und $\lim\limits_{x\to +\infty}$ $A(x)$ beschriebenen Eigenschaften (vgl. Aufgabe 3a).
hinsichtlich der momentanen Änderungsrate des Flächeninhalts zu Beobachtungsbeginn (vgl. Aufgabe 3c).

Skizziere - ausgehend von diesem Vergleich - in der Abbildung 2 den Graphen einer Funktion, die eine mögliche zeitliche Entwicklung des Flächeninhalts des Algenteppichs am Nordufer beschreibt.

(4 BE)

(40 BE)

Die Ableitung $\(f_{a,b}$ ist immer negativ und somit ist $\(f_{a,b}$ . Dadurch ist der Graph streng monoton abnehmend.

Da $\mathrm e^{-bx}\gt 0$ ist, sind die zugehörigen Funktionswerte von $f_{a,b}$ stets größer Eins. Somit nimmt der Graph nie den Wert $y=1$ an, sondern nähert sich immer weiter an $y=1$ an, ohne $y=1$ zu berühren. Deshalb ist $y=1$ eine waagrechte Asymptote.

Setze die Koordinaten in die Schar ein.

$\text{I} \quad 2= 1+ a \cdot \mathrm e^{-b}$

$\text{II} \quad 1,5=1+a \cdot \mathrm e^{-2b}$

$\begin{array}[t]{rll} 1,5&=& 1+a \cdot \mathrm e^{-2b}&\quad \scriptsize \mid\; -1 \\[5pt] 0,5&=& a \cdot \mathrm e^{-2b}&\quad \scriptsize \mid\; : \mathrm e^{-1,5b} \\[5pt] a&=&\dfrac{0,5}{ \mathrm e^{-2b}} \end{array}$

Setzt du a in $\text{I}$ erhältst du $b \approx 0,68$ .
Damit erhältst du $a\approx 1,95$ .

Keiner der Graphen der Funktionsschar enthält den Punkt mit den Koordinaten $(4 \mid 0,5)$ , da die $y=1$ die Asymptote darstellt. In der Funktionsschar nimmt keine Funktion Funktionswerte $y \leq 1$ an.

Der Graph der Funktion f geht aus der Exponentialfunktion durch Streckung um $-0,2$ in x-Richtung, Streckung um $7$ in y-Richtung und Verschiebung um 1 in y-Richtung hervor.

Diagramm mit einer Kurve und einem Rechteck im Koordinatensystem. Achsen sind beschriftet.

Den Flächeninhalt eines Rechtecks berechnest du mit: $A= a \cdot b$
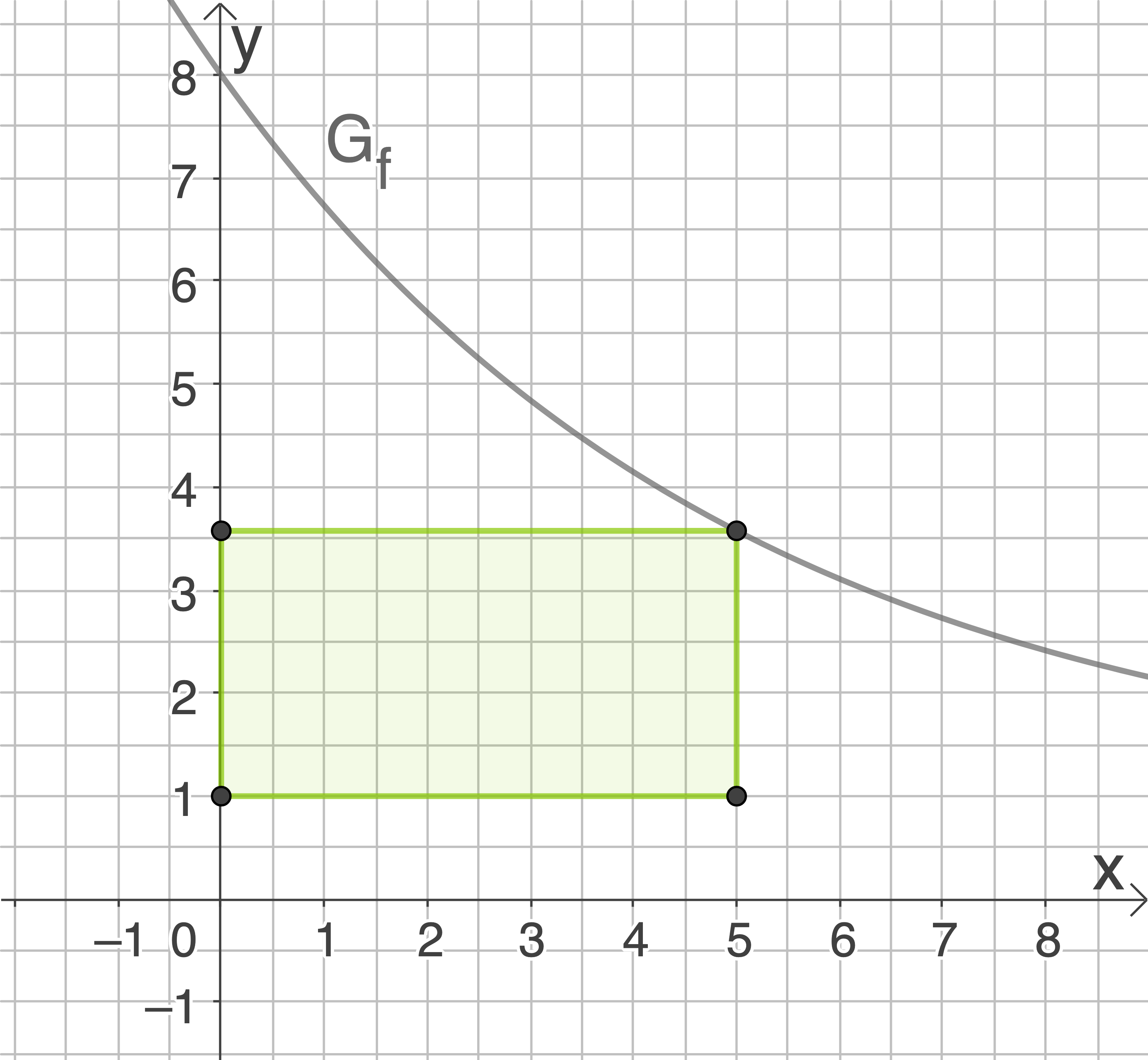
Bei diesem Rechteck gilt: $R(s)= (f(s)-1) \cdot s= (1+7 \mathrm e^{-0,2s} -1) \cdot s = 7s \cdot \mathrm e^{-0,2s}$

Um zu untersuchen, wo der Flächeninhalt maximal wird, musst du berechnen wo $R(s)$ ein Maximum hat.
Bestimme die erste Ableitung und wende das notwendige Kriterium für Extremstellen an.

$\(R$ $= -1,4s \cdot \mathrm e^{-0,2s} +7 \cdot \mathrm e^{-0,2s}$

$\(\begin{array}[t]{rll} 0&=& R$

Mit dem hinreichenden Kriterium für Extremstellen gilt:

$\(R$ $= 0,28s \cdot \mathrm e^{-0,2s} -2,8 \mathrm e^{-0,2s}$

Mit $\(R$ ist das Maximum bei $s=5$ .

Der maximale Flächeninhalt beträgt $R(5)\approx 12,88$

Den Flächeninhalt berechnest du mit $A(s)= \displaystyle\int_{0}^{s} (f(x) -1)\mathrm dx = \displaystyle\int_{0}^{s} ( 7 \mathrm e^{-0,2x}) \mathrm dx = \left [-35 \mathrm e^{-0,2x}\right]_0^s =-35 \mathrm e^{-0,2s} +35$ .

Die Stammfunktion von f lautet $F(x)= -35 \mathrm e^{-0,2x}$ .
Um den Wert für $s$ zu bestimmen, an dem der Flächeninhalt des Rechtecks 50% beträgt, musst du das Integral nach $s$ auflösen.

$\begin{array}[t]{rll} \dfrac{R(s)}{A(s)} &=& 0,5&\quad \scriptsize \\[5pt] \dfrac{7s \cdot \mathrm e^{-0,2s}}{-35 \mathrm e^{-0,2s} +35}&=& 0,5&\quad \scriptsize \mid\; CAS\\[5pt] s&\approx&6,27 \end{array}$

$A(x)= \dfrac{8}{f(x)} = \dfrac{8}{1+ 7 \mathrm e^{-0,2x}}$

$A(0) =1$

$\lim\limits_{x\to+\infty} A(x)$ $= \lim\limits_{x\to+\infty}\dfrac{8}{1+ 7 \mathrm e^{-0,2x}}$ $= \dfrac{8}{1+7 \cdot 0}$ $= \dfrac{8}{1} =8$

$f(x)$ ist monoton fallend. Da $f(x)$ im Nenner steht, ist $\dfrac{8}{f(x)}$ monoton wachsend. Somit wird $A(x)$ stetig größer und nähert sich $y=8$ an.

Setzt du $y= \dfrac{8}{f(x)}$ und löst nach $x$ auf, so kommst du auf die Umkehrfunktion $A^{-1}(x)= -5 \cdot \ln \left(\dfrac{8}{7x}-\dfrac{1}{7}\right)$ .

Bei der Umkehrfunktion sind Definitions- und Wertemenge der Ausgangsfunktion vertauscht. $A(x)$ ist in $\mathbb{R}_0^+$ definiert, also ist der Wertebereich von $A^{-1}$ $\mathbb{R}_0^+$ .

Der Definitionsbereich von $A^{-1}$ lautet $\mathbb{D} := \{x \in \mathbb{R} \mid 0 \lt x \lt 8 \}$ .

$x$ beschreibt den Flächeninhalt den der Algenteppich einnimmt. $A^{-1}$ ist dann die Anzahl der vergangenen Tagen nach denen der Algenteppich den Flächeninhalt $x$ erreicht hat.

Die Ableitung von $A(x)$ lautet:

$\(A$

Setze $x=0$ in die erste Ableitung, um die momentane Änderungsrate des Flächeninhalts zu Beobachtungsbeginn zu berechnen.

$\(A$

Der Graph von A hat im Punkt $(9,7 \mid 7,3)$ einen Wendepunkt.
Der Graph ändert im Wendepunkt sein Krümmungsverhalten von linksgekrümmt nach rechtsgekrümmt.

Der Graph von A sieht so aus.

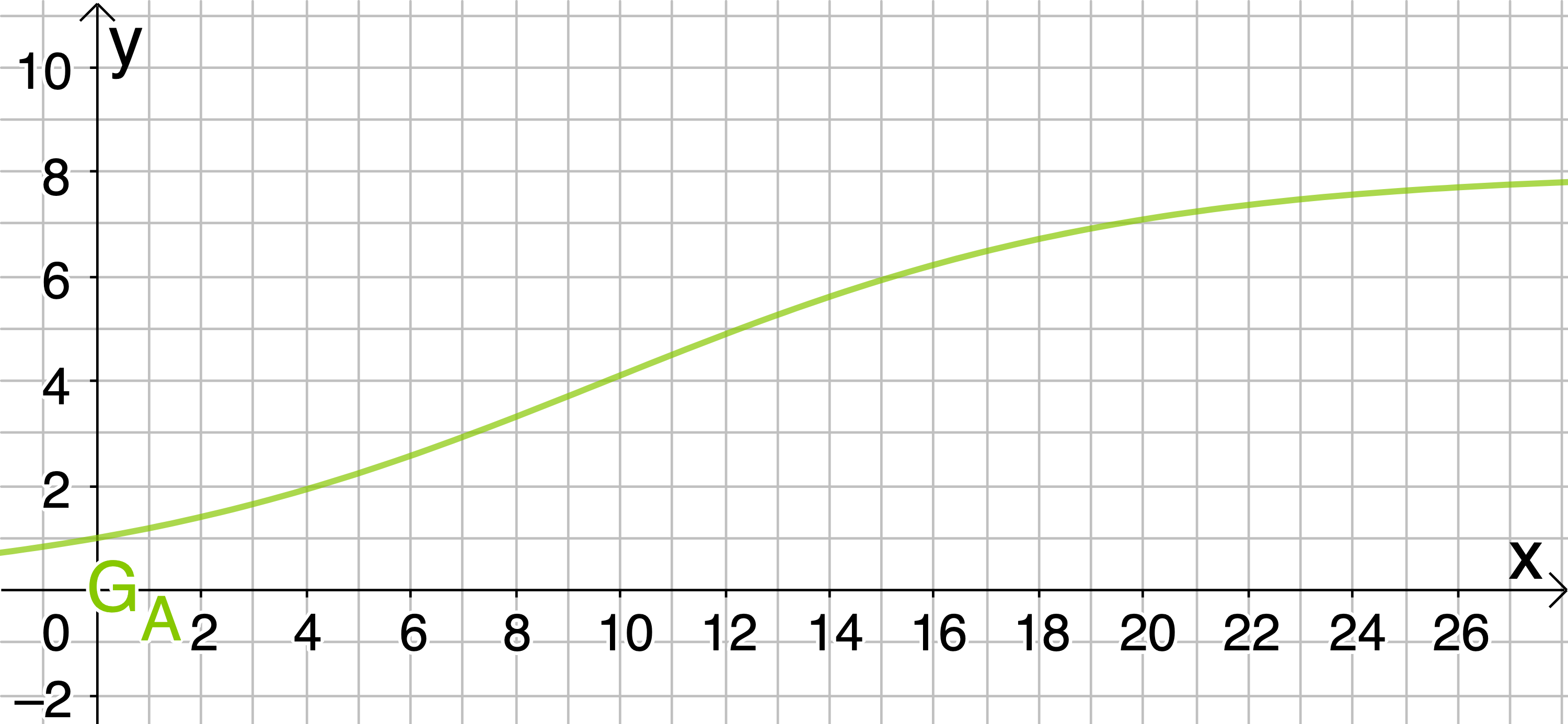
Graph mit aufsteigender Kurve in grün, Achsen beschriftet mit x und y.

Die Funktion lautet dann $A_b(x)= \dfrac{8}{1+ 7e^{-bx}}$ mit $-b\lt -0,2.$

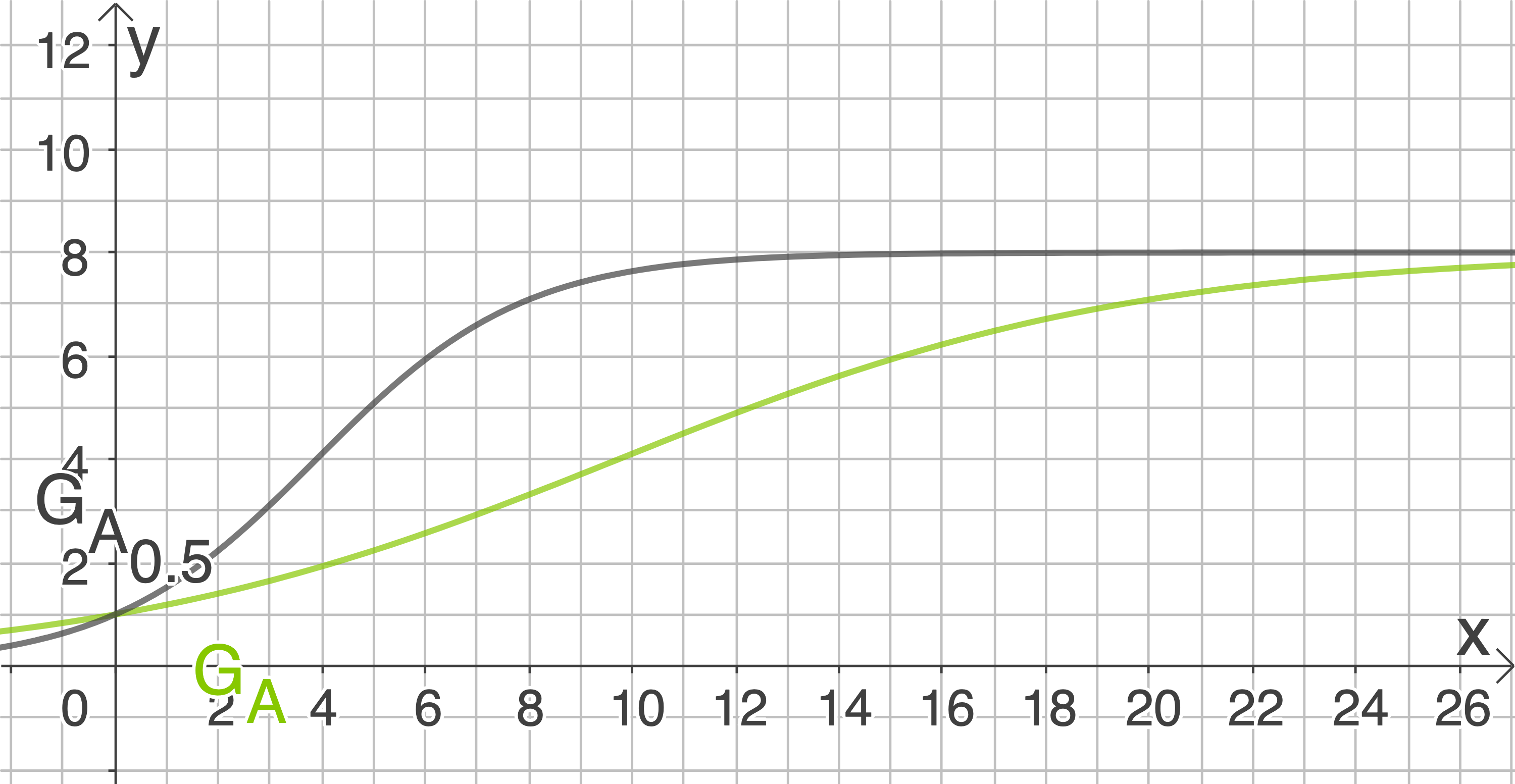
Die Funktionen haben denselben y-Achsenabschnitt. Es gilt also $A_b(0)=1=A(0)$ . Die Funktionen steigen monoton und nähern sich $y=8$ asymptotisch an. Somit ist auch das Grenzwertverhalten gleich $\lim\limits_{x\to+\infty} A_b(x)=\lim\limits_{x\to+\infty} A(x)= 8$ .
Je kleiner $-b$ wird, desto größer ist der die momentane Änderungsrate des Flächeninhalts zu Beobachtungsbeginn von $A_b(x)$ . Der Graph von $A_b(x)$ steigt deshalb in $x=0$ steiler an als der Graph von $A(x)$ in $x=0$ .

In der Abbildung ist der Graph für $-b=-0,5$ , also $\dfrac{8}{1+ 7e^{-0,5x}}$ dargestellt.

Graph mit zwei Kurven in unterschiedlichen Farben, dargestellt auf einem Koordinatensystem.