Teil B
1
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen
 mit
mit  Der Graph von
Der Graph von  wird mit
wird mit  bezeichnet.
bezeichnet.
a)
Gib die beiden Nullstellen von  an und begründe, dass
an und begründe, dass  im Bereich zwischen den Nullstellen oberhalb der
im Bereich zwischen den Nullstellen oberhalb der  -Achse verläuft.
-Achse verläuft.
(3 BE)
b)
Für alle 

 gilt
gilt  Deute diese Aussage geometrisch.
Deute diese Aussage geometrisch.
(2 BE)
c)
Für einen bestimmten Wert von  ist die Tangente an
ist die Tangente an  im Punkt
im Punkt  eine Gerade mit Steigung 1. Bestimme diesen Wert von
eine Gerade mit Steigung 1. Bestimme diesen Wert von  und weise nach, dass diese Gerade noch in einem weiteren Punkt Tangente an den zu diesem Wert von
und weise nach, dass diese Gerade noch in einem weiteren Punkt Tangente an den zu diesem Wert von  gehörenden Graphen
gehörenden Graphen  ist.
ist.
(4 BE)
d)
Gib die Anzahl der Wendepunkte von  in Abhängigkeit von
in Abhängigkeit von  an und begründe deine Angabe.
an und begründe deine Angabe.
(5 BE)
e)
Gib die  -Koordinate und die Art des Extrempunkts von
-Koordinate und die Art des Extrempunkts von  an.
an.
(2 BE)
2
Betrachtet wird die Funktion  mit maximaler Definitionsmenge
mit maximaler Definitionsmenge  wobei
wobei  die Funktion der Schar aus Aufgabe 1 mit
die Funktion der Schar aus Aufgabe 1 mit  ist.
ist.
 betrachtet, deren Definitionsmenge mit
betrachtet, deren Definitionsmenge mit  übereinstimmt.
übereinstimmt.
 und
und  schließen ein Flächenstück ein. Rotiert dieses Flächenstück um die
schließen ein Flächenstück ein. Rotiert dieses Flächenstück um die  -Achse, so entsteht ein Körper. Der Körper stellt modellhaft einen Asteroiden dar, das Flächenstück einen Längsschnitt durch den Asteroiden. Dabei entspricht eine Längeneinheit zehn Metern in der Realität.
-Achse, so entsteht ein Körper. Der Körper stellt modellhaft einen Asteroiden dar, das Flächenstück einen Längsschnitt durch den Asteroiden. Dabei entspricht eine Längeneinheit zehn Metern in der Realität.
Für eine Forschungsmission wird die Landung einer Raumsonde auf dem Asteroiden geplant. Der Landeanflug soll entlang einer Gerade erfolgen, die im Modell durch den Graphen der in definierten Funktion
definierten Funktion
 repräsentiert wird. Der Punkt
repräsentiert wird. Der Punkt  mit
mit  stellt den Landepunkt dar.
stellt den Landepunkt dar.
 Meter vom Landepunkt entfernt ist. Diese Position wird im Modell durch den Punkt
Meter vom Landepunkt entfernt ist. Diese Position wird im Modell durch den Punkt  dargestellt.
dargestellt.
a)
Gib  an.
an.
(1 BE)
b)
Betrachtet wird folgende Aussage:
Sind  und
und  zwei in einem Intervall
zwei in einem Intervall  definierte differenzierbare Funktionen, für die
definierte differenzierbare Funktionen, für die  und
und  für alle
für alle  gilt, so besitzen
gilt, so besitzen  und
und  das gleiche Monotonieverhalten.
Zeige, dass die Aussage richtig ist, und gib die Koordinaten des Hochpunkts des Graphen von
das gleiche Monotonieverhalten.
Zeige, dass die Aussage richtig ist, und gib die Koordinaten des Hochpunkts des Graphen von  an.
an.
(4 BE)
c)
Gib  und
und  an und interpretiere das Ergebnis geometrisch.
an und interpretiere das Ergebnis geometrisch.
Zusätzlich wird die Funktion
(3 BE)
d)
Skizziere die Graphen von  und
und  unter Verwendung der bisherigen Ergebnisse in einem Koordinatensystem.
unter Verwendung der bisherigen Ergebnisse in einem Koordinatensystem.
Die Graphen von
(3 BE)
Für eine Forschungsmission wird die Landung einer Raumsonde auf dem Asteroiden geplant. Der Landeanflug soll entlang einer Gerade erfolgen, die im Modell durch den Graphen der in
e)
Bestimme  und deute die Gleichung
und deute die Gleichung  im Sachzusammenhang.
[Zur Kontrolle:
im Sachzusammenhang.
[Zur Kontrolle:  ]
]
Die Bremsdüsen der Raumsonde werden an der Position aktiviert, die
(4 BE)
f)
Bestimme rechnerisch die Koordinaten von  auf zwei Dezimalen genau.
[Zur Kontrolle:
auf zwei Dezimalen genau.
[Zur Kontrolle:  -Koordinate von
-Koordinate von  etwa
etwa  ]
]
(4 BE)
g)
Rotiert ein Flächenstück, das vom Graphen einer in ![\([c;d]\)](https://mathjax.schullv.de/c5102de277c9715e6addadb55b6951af54c77d495e861fb02dec880a007d97cd?color=5a5a5a) definierten Funktion
definierten Funktion  mit Nullstellen
mit Nullstellen  und
und  und der
und der  -Achse eingeschlossen wird, um die
-Achse eingeschlossen wird, um die  -Achse, so entsteht ein rotationssymmetrischer Körper, dessen Schwerpunkt auf der
-Achse, so entsteht ein rotationssymmetrischer Körper, dessen Schwerpunkt auf der  -Achse liegt. Für die
-Achse liegt. Für die  -Koordinate
-Koordinate  des Schwerpunkts gilt dabei:
des Schwerpunkts gilt dabei:
 Bestimme die
Bestimme die  -Koordinate des Schwerpunkts
-Koordinate des Schwerpunkts  des Rotationskörpers, der den Asteroiden beschreibt, auf zwei Dezimalen genau.
des Rotationskörpers, der den Asteroiden beschreibt, auf zwei Dezimalen genau.
Berechne die Größe des Winkels, um die sich die Flugbahn ändert, wenn der letzte Teil des Landeanflugs – anders als ursprünglich geplant – entlang einer Gerade erfolgt, die im Modell durch die Gerade dargestellt wird.
dargestellt wird.
Berechne die Größe des Winkels, um die sich die Flugbahn ändert, wenn der letzte Teil des Landeanflugs – anders als ursprünglich geplant – entlang einer Gerade erfolgt, die im Modell durch die Gerade
(5 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Nullstellen angeben
Mit dem Satz vom Nullprodukt folgt:
 und somit
und somit  und
und  Außerdem gilt:
Außerdem gilt:
 , da
, da  und
und  Verlauf begründen
Ausmultipliziert ist der Term mit dem höchsten Exponenten
Verlauf begründen
Ausmultipliziert ist der Term mit dem höchsten Exponenten  der Graph nimmt folglich die Form einer nach unten geöffneten Parabel an. Für
der Graph nimmt folglich die Form einer nach unten geöffneten Parabel an. Für  gilt
gilt  also verläuft der Graph in diesem Bereich oberhalb der
also verläuft der Graph in diesem Bereich oberhalb der  -Achse.
-Achse.
b)
Die Steigungen aller Graphen der Schar haben an der Stelle  den gleichen Wert. Die Tangente an dieser Stelle ist somit für jedes
den gleichen Wert. Die Tangente an dieser Stelle ist somit für jedes  identisch.
identisch.
c)
Wert von  bestimmen
bestimmen
 Weiteren Punkt bestimmen
Tangentengleichung aufstellen:
Weiteren Punkt bestimmen
Tangentengleichung aufstellen:
 Tangente mit
Tangente mit  schneiden:
schneiden:
![\(\begin{array}[t]{rll}
y&=& f_{25}(x) &\\[5pt]
x&=& -\dfrac{1}{250}\cdot \left(x^4-10x^3+25 x^2-250x\right)
\end{array}\)](https://mathjax.schullv.de/4694711e027502e9ddf6c13c802fcccb2fa99b49e654ae4a4e3f10a3476f32a7?color=5a5a5a) Mit dem solve-Befehl des CAS folgt
Mit dem solve-Befehl des CAS folgt 
 Die Steigung im Punkt
Die Steigung im Punkt  ergibt sich zu
ergibt sich zu  Die Gerade ist folglich zusätzlich Tangente im Punkt
Die Gerade ist folglich zusätzlich Tangente im Punkt 
d)
Notwendige Bedingung für Wendepunkte anwenden
Mit der Mitternachtsformel folgt:
Für  folgt
folgt  und somit keine Wendepunkte.
Für
und somit keine Wendepunkte.
Für  folgt
folgt  und somit eine Wendepunkte.
Für
und somit eine Wendepunkte.
Für  folgt
folgt  und somit zwei Wendepunkte.
und somit zwei Wendepunkte.
e)
2.
a)
Es dürfen nur Werte von  eingesetzt werden, für welche der Radikand positiv ist.
Dies ist nur im Bereich
eingesetzt werden, für welche der Radikand positiv ist.
Dies ist nur im Bereich  1 a) folgt:
1 a) folgt:

b)
Ableitung  berechnen
Mit der Kettenregel ergibt sich:
berechnen
Mit der Kettenregel ergibt sich:
 Monotonie bestimmen
Es gilt
Monotonie bestimmen
Es gilt  Für
Für  folgt somit
folgt somit  .
Für
.
Für  folgt
folgt  .
Für
.
Für  folgt somit
folgt somit  .
Die Aussage ist somit richtig.
Koordinaten des Hochpunkts angeben
Da das Monotonieverhalten von
.
Die Aussage ist somit richtig.
Koordinaten des Hochpunkts angeben
Da das Monotonieverhalten von  und
und  für
für  folglich gleich ist, ist
folglich gleich ist, ist  genau dann, wenn
genau dann, wenn  Aus 1 e) folgt:
Aus 1 e) folgt:  gilt für
gilt für  und beschreibt einen Hochpunkt.
und beschreibt einen Hochpunkt.
 -Koordinate berechnen:
Der Hochpunkt des Graphen von
-Koordinate berechnen:
Der Hochpunkt des Graphen von  besitzt die Koordinaten
besitzt die Koordinaten 
c)
Grenzwerte berechnen

 Geometrische Interpretation
Der Graph von
Geometrische Interpretation
Der Graph von  schneidet die
schneidet die  -Achse in ihren Nullstellen senkrecht.
-Achse in ihren Nullstellen senkrecht.
d)
Die Monotonie von  ist wie in 2 b) gezeigt gleich wie bei
ist wie in 2 b) gezeigt gleich wie bei  , besitzt also die Form einer nach unten geöffneten Parabel.
Die Nullstellen
, besitzt also die Form einer nach unten geöffneten Parabel.
Die Nullstellen  und
und  und der Hochpunkt
und der Hochpunkt  ebenso wie der Definitionsbereich
ebenso wie der Definitionsbereich  wurden bereits berechnet.
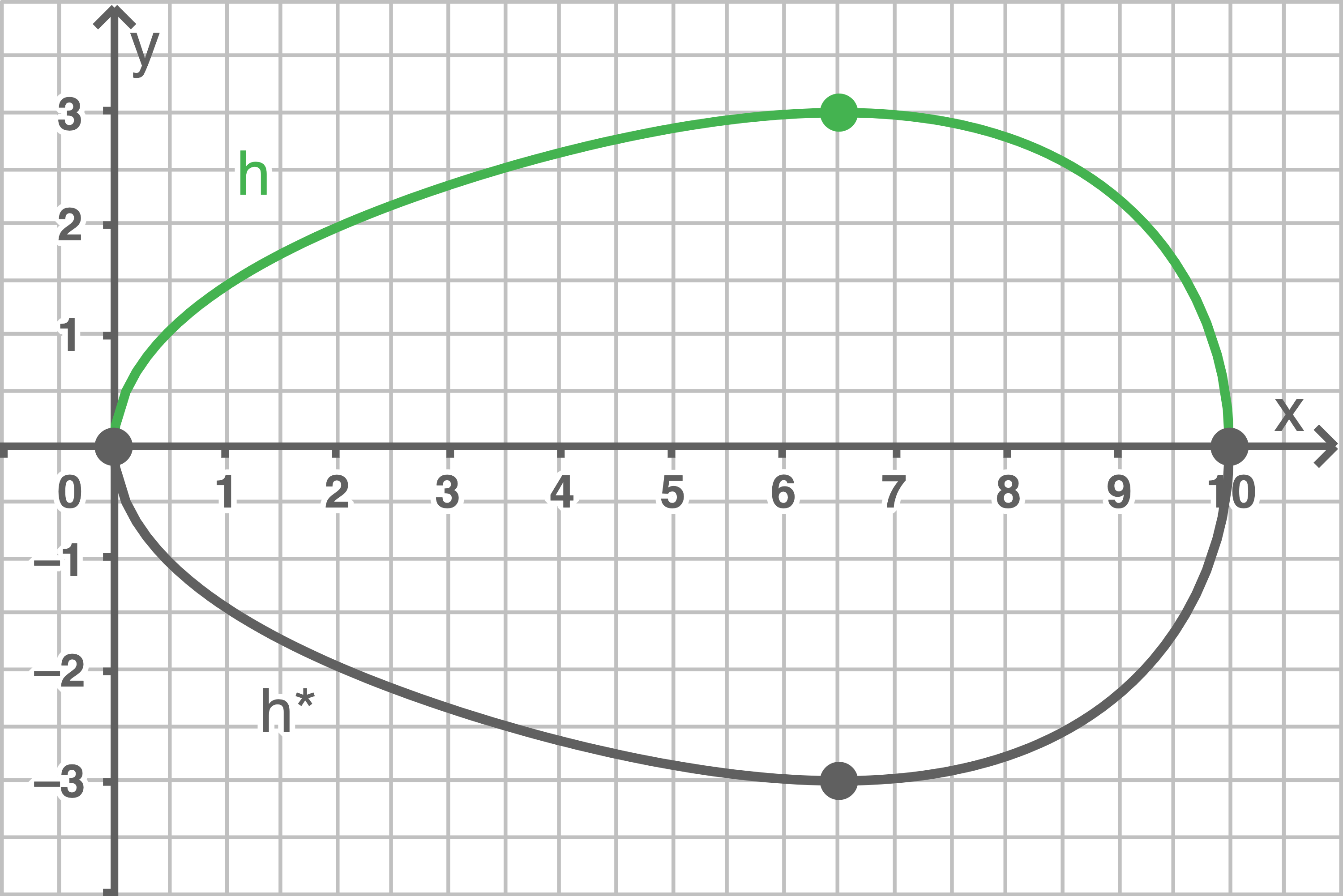
Der Graph von
wurden bereits berechnet.
Der Graph von  ergibt sich durch Spiegelung an der
ergibt sich durch Spiegelung an der  -Achse.
-Achse.

e)
f)
Mit dem solve-Befehl des CAS folgt: 
 -Koordinate bestimmen:
-Koordinate bestimmen:
![\(\begin{array}[t]{rll}
s(4,31)&=&\frac{1}{15} \sqrt{1830} \cdot(11-2\cdot 4,31) & \\[5pt]
&\approx& 6,79
\end{array}\)](https://mathjax.schullv.de/0baabf4f1b672b8acc5e408d112991e20c4c6391cc60e301a4989d0cfb563365?color=5a5a5a) Die Koordinaten von
Die Koordinaten von  entsprechen somit
entsprechen somit 
g)