Teil B
Gegeben sind die in  definierten Funktionen
definierten Funktionen  mit
mit  .
.
Der Graph von wird mit
wird mit  bezeichnet.
Im Folgenden ist
bezeichnet.
Im Folgenden ist  . Die zugehörige Funktion
. Die zugehörige Funktion  wird mit
wird mit  bezeichnet, d.h.
bezeichnet, d.h.  .
.
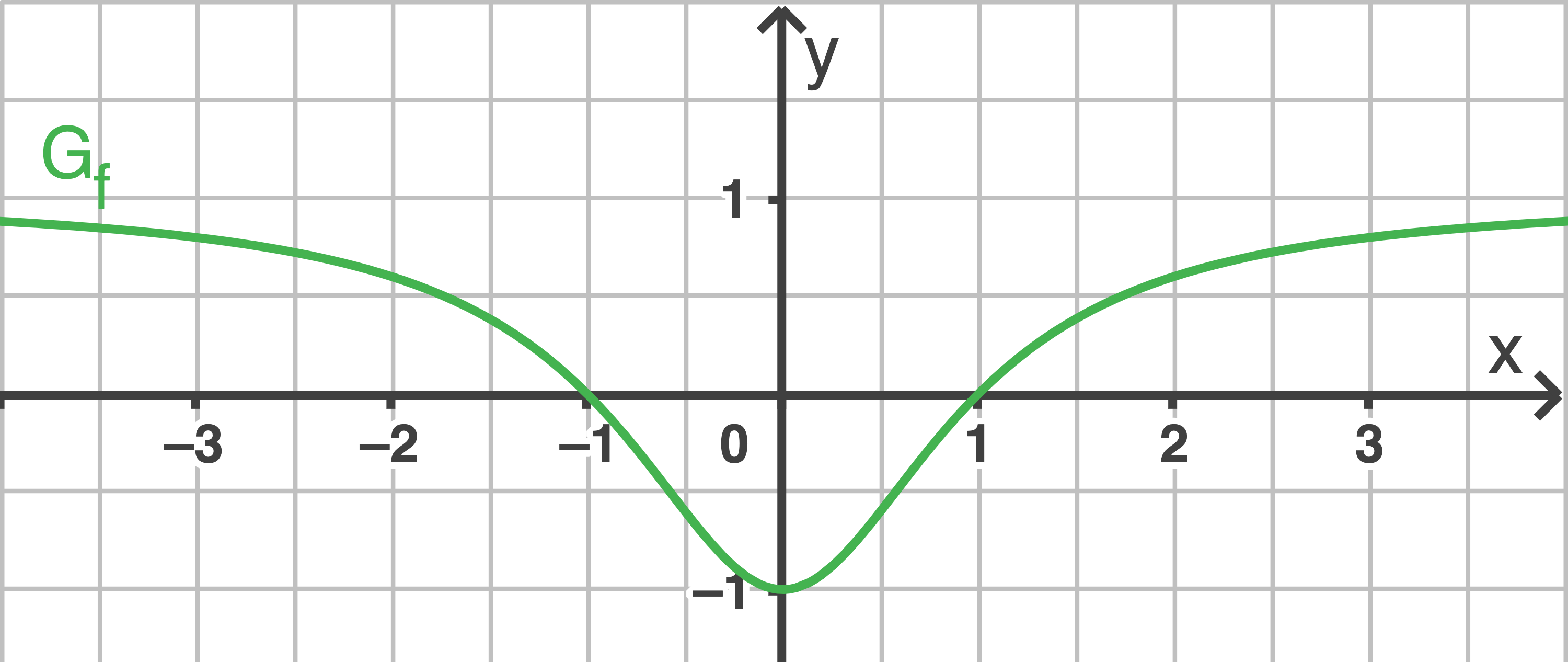
Die Abbildung 1 zeigt ihren Graphen
Der Graph von
1
a)
Bestätige rechnerisch, dass  für jeden Wert von
für jeden Wert von  symmetrisch bezüglich der
symmetrisch bezüglich der  -Achse ist, und gib in Abhängigkeit von
-Achse ist, und gib in Abhängigkeit von  den Grenzwert von
den Grenzwert von  für
für  an.
an.
(2 BE)
b)
Bestimme rechnerisch in Abhängigkeit von  Lage und Art des Extrempunkts von
Lage und Art des Extrempunkts von  und gib das Monotonieverhalten von
und gib das Monotonieverhalten von  an.
an.
(5 BE)
c)
Bestimme denjenigen Wert von  , für den die von
, für den die von  und
und  eingeschlossene Fläche den Inhalt
eingeschlossene Fläche den Inhalt  hat.
hat.
(4 BE)
Die Abbildung 1 zeigt ihren Graphen
2
a)
Gib die Anzahl der Lösungen der Gleichung  mit
mit  in Abhängigkeit von
in Abhängigkeit von  an und begründe deine Angabe.
an und begründe deine Angabe.
(4 BE)
b)
Bestimme rechnerisch die Gleichungen aller Tangenten an  , die den Punkt
, die den Punkt  enthalten.
enthalten.
(5 BE)
3
Nun wird die in  definierte Integralfunktion
definierte Integralfunktion  betrachtet; ihr Graph wird mit
betrachtet; ihr Graph wird mit  bezeichnet.
bezeichnet.
 definierte Funktion
definierte Funktion  stellt in einem gewissen Bereich eine gute Näherung für die Funktion
stellt in einem gewissen Bereich eine gute Näherung für die Funktion  dar.
dar.
a)
Begründe, dass  in
in  eine Nullstelle hat, und mache mithilfe des Verlaufs von
eine Nullstelle hat, und mache mithilfe des Verlaufs von  plausibel, dass im Intervall
plausibel, dass im Intervall ![\([1;3]\)](https://mathjax.schullv.de/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c?color=5a5a5a) eine weitere Nullstelle von
eine weitere Nullstelle von  liegt.
liegt.
Gib an und begründe, dass der Punkt
an und begründe, dass der Punkt  Hochpunkt von
Hochpunkt von  ist.
ist.
Gib
(5 BE)
b)
Eine der Tangenten aus Aufgabe 2b verläuft durch den Punkt  und begrenzt gemeinsam mit den Koordinatenachsen ein Dreieck. Zeichne dieses Dreieck in die Abbildung 1 ein. Gib den Flächeninhalt dieses Dreiecks und den sich daraus ergebenden Näherungswert für
und begrenzt gemeinsam mit den Koordinatenachsen ein Dreieck. Zeichne dieses Dreieck in die Abbildung 1 ein. Gib den Flächeninhalt dieses Dreiecks und den sich daraus ergebenden Näherungswert für  an. Berechne die prozentuale Abweichung dieses Näherungswerts von
an. Berechne die prozentuale Abweichung dieses Näherungswerts von  .
.
Die in
(4 BE)
c)
Beschreibe, wie der Graph von  aus dem Graphen der in
aus dem Graphen der in  definierten Funktion
definierten Funktion  hervorgeht. Berechne durch Integration von
hervorgeht. Berechne durch Integration von  einen weiteren Näherungswert für
einen weiteren Näherungswert für  .
.
(4 BE)
4
Für jeden Wert  legen die auf
legen die auf  liegenden Punkte
liegenden Punkte  und
und  gemeinsam mit dem Punkt
gemeinsam mit dem Punkt  ein gleichschenkliges Dreieck
ein gleichschenkliges Dreieck  fest.
fest.
a)
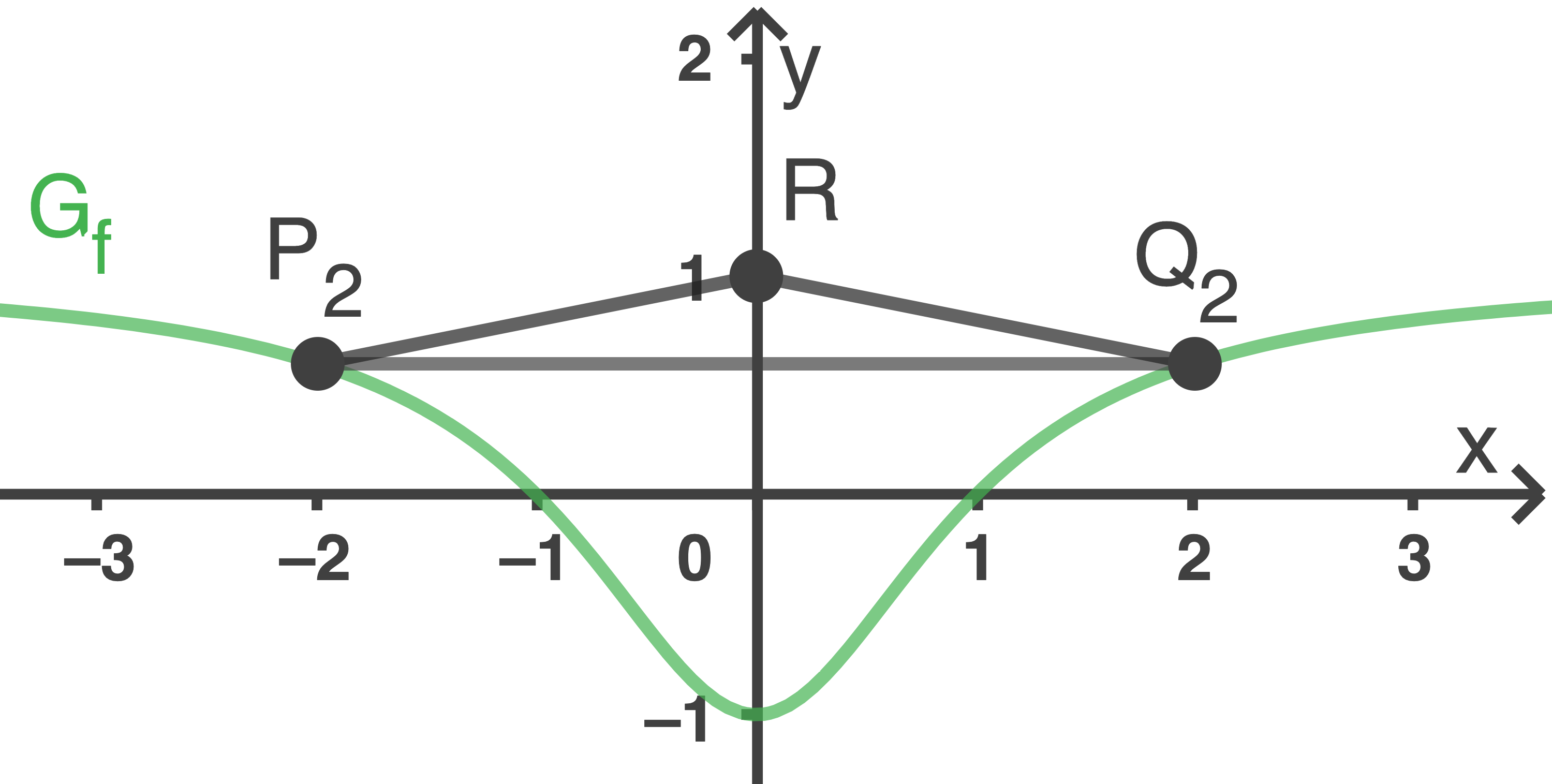
Berechne für  den Flächeninhalt des zugehörigen Dreiecks
den Flächeninhalt des zugehörigen Dreiecks  (vgl. Abbildung 2).
Zeige anschließend, dass der Flächeninhalt des Dreiecks
(vgl. Abbildung 2).
Zeige anschließend, dass der Flächeninhalt des Dreiecks  allgemein durch den Term
allgemein durch den Term  beschrieben werden kann.
beschrieben werden kann.
(4 BE)
b)
Zeige, dass es einen Wert von  gibt, für den
gibt, für den  maximal ist.
maximal ist.
Berechne diesen Wert von sowie den Flächeninhalt des zugehörigen Dreiecks
sowie den Flächeninhalt des zugehörigen Dreiecks  .
.
Berechne diesen Wert von
(3 BE)
(40 BE)
1
a)
Die Funktion ist symmetrisch zur y-Achse, wenn  gilt.
Mit
gilt.
Mit  ist die Funktion symmetrisch zur y-Achse.
Für
ist die Funktion symmetrisch zur y-Achse.
Für  gilt
gilt  .
.
b)
Extrempunkt
 Wende die Quotientenregel an um die ersten beiden Ableitungen von
Wende die Quotientenregel an um die ersten beiden Ableitungen von  zu bestimmen. Die Ableitungen von
zu bestimmen. Die Ableitungen von  lauten:
lauten:

 Wende nun das notwendige Kriterium für Extremstellen an.
Wende nun das notwendige Kriterium für Extremstellen an.
![\(\begin{array}[t]{rll}
0&=&\dfrac{4x}{a \cdot(x^2+1)^2} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/23eafd1729804a9a54da93abfaf5c8402bfd2e29c6deea7164721cb4bdbaffa2?color=5a5a5a) Daraus folgt
Daraus folgt  .
Wende das hinreichende Kriterium für Extremstellen an.
Wegen
.
Wende das hinreichende Kriterium für Extremstellen an.
Wegen 
 ,
,  und mit
und mit  befindet sich ein Tiefpunkt in
befindet sich ein Tiefpunkt in  Monotonieverhalten
Das Monotonieverhalten einer Funktion
Monotonieverhalten
Das Monotonieverhalten einer Funktion  kannst du über ihre erste Ableitung bstimmen. Ist
kannst du über ihre erste Ableitung bstimmen. Ist  ist
ist  monoton steigend, ist
monoton steigend, ist  so ist
so ist  monoton fallend.
monoton fallend.
 Für
Für  , (wegen
, (wegen  ) gilt: Ist
) gilt: Ist  , so ist
, so ist  und für
und für  ist
ist  .
Für
.
Für  ist
ist  streng monoton fallend und für
streng monoton fallend und für  ist
ist  streng monoton steigend.
streng monoton steigend.
c)
Den Flächeninhalt berechnest du mit einem Integral. Die Integrationsgrenzen des Integrals stellen die Schnittstellen von  und
und  dar. Berechne diese zuerst. Verwende dafür den solve-Befehl deines CAS-Rechners.
dar. Berechne diese zuerst. Verwende dafür den solve-Befehl deines CAS-Rechners.
![\(\begin{array}[t]{rll}
f_a(x)&=& f_2(x)&\quad \scriptsize \mid\; CAS \\[5pt]
x_1&=& -1&\quad \scriptsize \\[5pt]
x_1&=&1
\end{array}\)](https://mathjax.schullv.de/16ef44de60b7e002e1627ad0a316d4358bd3668fa4626b726baa7f7fb3918e25?color=5a5a5a) Setze nun die Integrationsgrenzen in das Integral mit den Funktionen ein und setzte dieses gleich
Setze nun die Integrationsgrenzen in das Integral mit den Funktionen ein und setzte dieses gleich  .
.
![\(\begin{array}[t]{rll}
\displaystyle\int_{-1}^{1} \left(f_a(x)-f_2(x) \right) \mathrm dx&=& 2 \pi -4&\quad \scriptsize \mid\; CAS \\[5pt]
a&=&\dfrac{2}{5}
\end{array}\)](https://mathjax.schullv.de/9cecfc0e7b70f2ec32b9218f54de2b7f06ec8c7b353ba2c7a810ba12178ca67a?color=5a5a5a)
2
a)
Die Lösungen  sind die Schnittstellen der Geraden
sind die Schnittstellen der Geraden  und der Funktion
und der Funktion  dar. Der Graph von
dar. Der Graph von  nähert sich asymptotisch
nähert sich asymptotisch  an, die tiefste Stelle liegt bei
an, die tiefste Stelle liegt bei  . Das bedeutet, dass es nur im Bereich zwischen
. Das bedeutet, dass es nur im Bereich zwischen  und
und  Schnittstellen geben kann. Außerhalb dieses Bereichs nicht.
Im tiefsten Punkt
Schnittstellen geben kann. Außerhalb dieses Bereichs nicht.
Im tiefsten Punkt  kann es nur eine Schnittstelle geben, ansonsten zwei, da der Graph der Funktion achsensymmetrisch ist.
kann es nur eine Schnittstelle geben, ansonsten zwei, da der Graph der Funktion achsensymmetrisch ist.
und
: es gibt keine Lösung
: es gibt eine Lösung
: es gibt zwei Lösungen
b)
Die allgemeine Tangentengleichung lautet  Es gilt
Es gilt  und
und  .
Setze nun
.
Setze nun  und
und  und die Koordinaten
und die Koordinaten  in
in  ein.
ein.
![\(\begin{array}[t]{rll}
-1&=&\dfrac{4a}{a^4+2a^2+1} \cdot (0-a) + \dfrac{a^2-1}{a^2+1}&\quad \scriptsize \\[5pt]
-1&=& \dfrac{-4a^2}{a^4+2a^2+1} + \dfrac{a^2-1}{a^2+1}&\quad \scriptsize \mid \text{CAS} \\[5pt]
a_1&=&-1 &\quad \scriptsize \\[5pt]
a_2&=&1 &\quad \scriptsize \\[5pt]
a_3&=&0
\end{array}\)](https://mathjax.schullv.de/bfbbb8082942e3114a03d7fa2064d255808565c1822ebc3ab0b7aa5d3b8c0245?color=5a5a5a) Setze nun
Setze nun  und
und  in
in  ein. Es ergeben sich die Gleichungen:
ein. Es ergeben sich die Gleichungen:



3
a)
Die Integralfunktion  beschreibt die Flächenbilanz der vom Graphen der Funktion
beschreibt die Flächenbilanz der vom Graphen der Funktion  und der x-Achse im Intervall
und der x-Achse im Intervall ![\([0;x]\)](https://mathjax.schullv.de/c8141eb4d1ded64a40ef6ef4c3a68eee74daa1b9d71543a808ea357efd59a28c?color=5a5a5a) eingeschlossenen Fläche. Für
eingeschlossenen Fläche. Für  wird keine Fläche eingeschlossen, daher muss
wird keine Fläche eingeschlossen, daher muss  sein.
Im Intervall
sein.
Im Intervall ![\([0;1] \)](https://mathjax.schullv.de/54d2742bd987d16409d1cddea42881b7832add7c482732d3f27f9161927764c9?color=5a5a5a) schließt
schließt  mit der x-Achse eine Fläche unterhalb der x-Achse ein. Da
mit der x-Achse eine Fläche unterhalb der x-Achse ein. Da  im Intervall
im Intervall ![\([1;x]\)](https://mathjax.schullv.de/2866aa6893c5b20757c7532cfd97a9b8f9cb976f0e86bcb707ca6bb3410bffa6?color=5a5a5a) monoton steigt, schließen
monoton steigt, schließen  und die x-Achse eine Fläche oberhalb der x-Achse ein.
und die x-Achse eine Fläche oberhalb der x-Achse ein.
Es existiert ein im Intervall
im Intervall ![\([1;3]\)](https://mathjax.schullv.de/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c?color=5a5a5a) , an dem die Flächen unterhalb und oberhalb der x-Achse den gleichen Flächeninhalt haben. Da diese gleich großen Flächen unterhalb und oberhalb der x-Achse liegen, sind die zugehörigen Integralwerte positiv und negativ und heben sich somit gegenseitig auf. Für dieses
, an dem die Flächen unterhalb und oberhalb der x-Achse den gleichen Flächeninhalt haben. Da diese gleich großen Flächen unterhalb und oberhalb der x-Achse liegen, sind die zugehörigen Integralwerte positiv und negativ und heben sich somit gegenseitig auf. Für dieses ![\(x \in [1;3]\)](https://mathjax.schullv.de/864d175377edc99e26b39f0a8704223c706ef6953446495e2c1f0810122a5f67?color=5a5a5a) ist
ist  . Somit existiert eine weitere Nullstelle von
. Somit existiert eine weitere Nullstelle von  im Intervall
im Intervall ![\([1;3]\)](https://mathjax.schullv.de/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c?color=5a5a5a) .
Bei
.
Bei  hat
hat  eine Nullstelle. Der Graph von
eine Nullstelle. Der Graph von  hat an dieser Stelle einen Hochpunkt, da
hat an dieser Stelle einen Hochpunkt, da  im Bereich von
im Bereich von  monoton fällt und es somit zu einem Vorzeichenwechsel von positiv zu negativ kommt.
monoton fällt und es somit zu einem Vorzeichenwechsel von positiv zu negativ kommt.
 .
.
Es existiert ein
b)
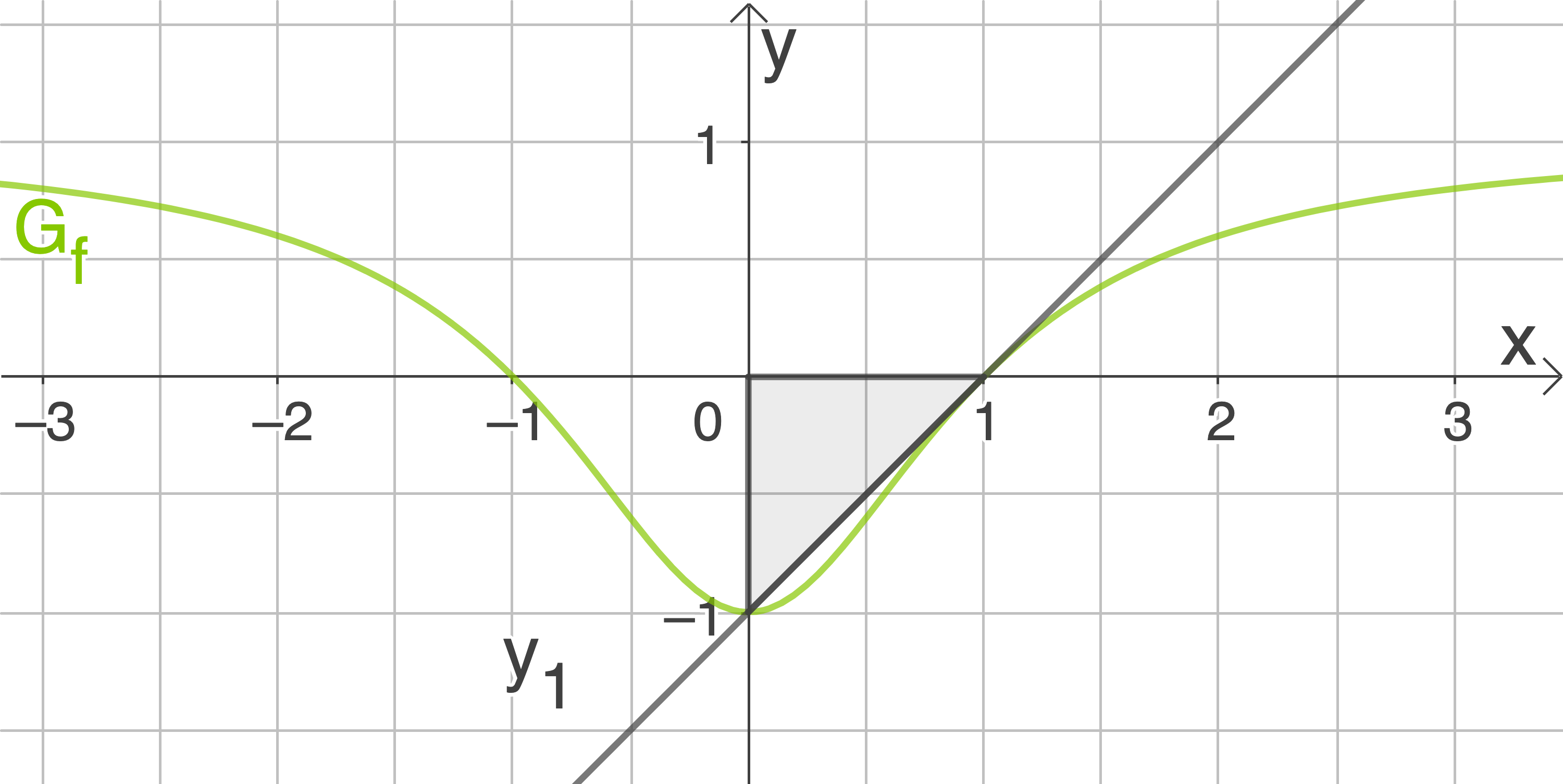
c)
4
a)
Den Flächeninhalt eines Dreiecks brechnest du mit  .
Für
.
Für  lauten die Punkte
lauten die Punkte  und somit ist
und somit ist  und
und  .
.
 Der allgemeine Flächeninhalt kann auch so berechnet werden:
Der allgemeine Flächeninhalt kann auch so berechnet werden:






b)
Berechne das Maximum mit deinem CAS Rechner.
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum