Wahlteil C1
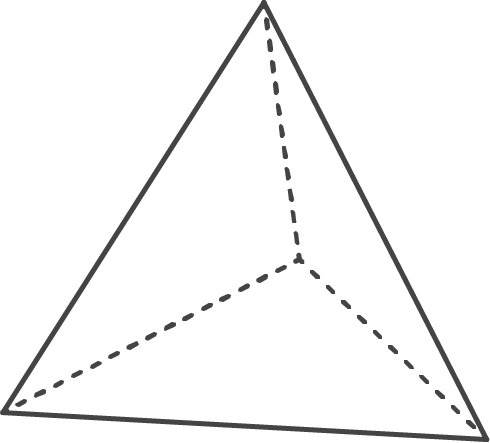
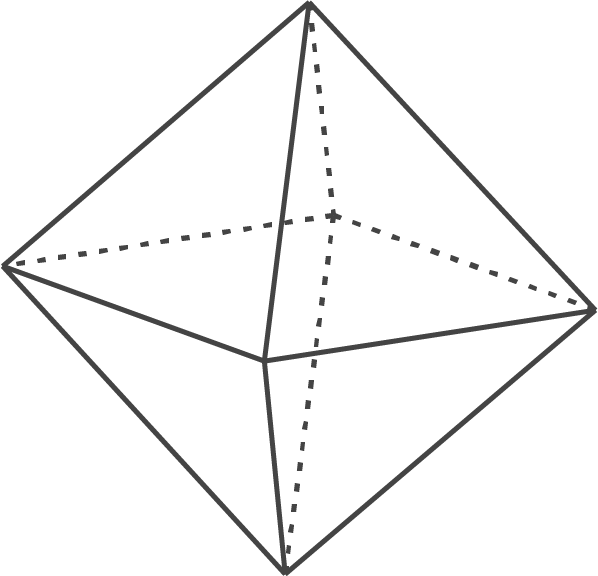
Betrachtet werden Körper, die auf jeder Seitenfläche mit einer Zahl beschriftet sind.
Beim Werfen eines Körpers gilt die Zahl als geworfen, auf der der Körper zum Liegen kommt. Dabei werden bei jedem Körper die möglichen Zahlen jeweils mit derselben Wahrscheinlichkeit geworfen.
| Körper | Tetraeder | Würfel | Oktaeder |
|---|---|---|---|
|
|
|
|
| Anzahl der Seitenflächen | vier | sechs | acht |
| beschriftet mit | 1, 2, 3, 4 | 1, 2, 3, 4, 5, 6 | 1, 2, 3, 4, 5, 6, 7, 8 |
a)
Ein Tetraeder wird  -mal geworfen.
-mal geworfen.
Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse. A: "Die Zahl wird genau
wird genau  -mal geworfen."
-mal geworfen."
B: "Die Zahl wird mindestens
wird mindestens  -mal geworfen."
-mal geworfen."
Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse. A: "Die Zahl
B: "Die Zahl
(1,5 VP)
b)
Ermittle, wie oft man ein Tetraeder mindestens werfen muss, um mit einer Wahrscheinlichkeit von mindestens  mindestens einmal die Zahl
mindestens einmal die Zahl  zu werfen.
zu werfen.
(2 VP)
c)
Ein Tetraeder, ein Würfel und ein Oktaeder werden gleichzeitig geworfen.
Berechne die Wahrscheinlichkeit der folgenden Ereignisse. C: "Bei allen drei Körpern wird dieselbe Zahl geworfen."
D: "Die Summe der geworfenen Zahlen beträgt ."
."
Berechne die Wahrscheinlichkeit der folgenden Ereignisse. C: "Bei allen drei Körpern wird dieselbe Zahl geworfen."
D: "Die Summe der geworfenen Zahlen beträgt
(2,5 VP)
d)
Für einen Einsatz von  darf ein Spieler ein Tetraeder und einen Würfel einmal werfen. Anschließend erhält er die Anzahl der geworfenen Einsen in Euro ausbezahlt.
darf ein Spieler ein Tetraeder und einen Würfel einmal werfen. Anschließend erhält er die Anzahl der geworfenen Einsen in Euro ausbezahlt.
Bestimme den Erwartungswert für den Gewinn des Spielers.
Bestimme den Erwartungswert für den Gewinn des Spielers.
(2 VP)
e)
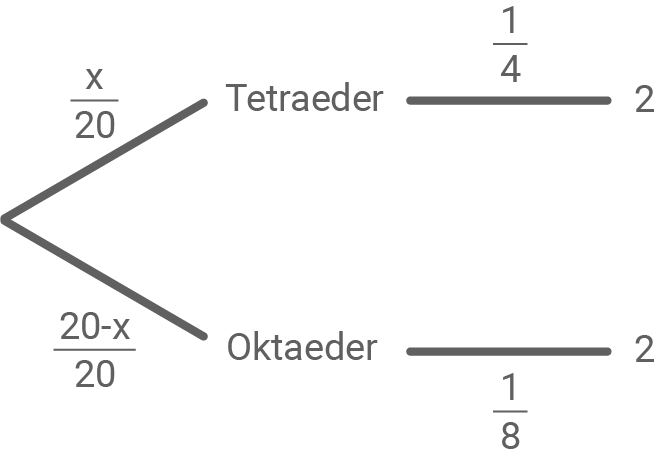
In einem Sack befinden sich  Körper. Es handelt sich dabei um Tetraeder oder Oktaeder, wie sie oben beschrieben sind. Einer dieser Körper wird zufällig gezogen und anschließend geworfen. Die Wahrscheinlichkeit, dabei die Zahl
Körper. Es handelt sich dabei um Tetraeder oder Oktaeder, wie sie oben beschrieben sind. Einer dieser Körper wird zufällig gezogen und anschließend geworfen. Die Wahrscheinlichkeit, dabei die Zahl  zu werfen, beträgt
zu werfen, beträgt  .
.
Berechne die Anzahl der Tetraeder im Sack.
Berechne die Anzahl der Tetraeder im Sack.
(2 VP)
a)
Wahrscheinlichkeiten berechnen
Betrachtet wird die Zufallsgröße  die die zufällige Anzahl der geworfenen Einsen bei
die die zufällige Anzahl der geworfenen Einsen bei  -maligem Werfen eines Tetraeders beschreibt. Diese kann als binomialverteilt mit
-maligem Werfen eines Tetraeders beschreibt. Diese kann als binomialverteilt mit  und
und  betrachtet werden.
betrachtet werden.
![\(\begin{array}[t]{rll}
P(A) &=& P(X=30)\\[5pt]
&=& \binom{100}{30} \cdot 0,25^{30}\cdot 0,75^{70} \\[5pt]
&\approx& 0,0458\\[5pt]
&=& 4,58\,\% \\[5pt]
P(B) &=& P(X\geq 20)\\[5pt]
&=& 1-P(X\leq 19) \\[5pt]
&\approx& 1-0,0995\\[5pt]
&=& 0,9005\\[5pt]
&=& 90,05\,\% \\[5pt]
\end{array}\)](https://mathjax.schullv.de/32689f412ab2aedb55e09bcf0ec1d340ee33df76c6585cb63f343bff74a8f8c9?color=5a5a5a)
b)
Anzahl Würfe ermitteln
Betrachtet wird die Zufallsgröße  die die zufällige Anzahl der geworfenen Einsen bei
die die zufällige Anzahl der geworfenen Einsen bei  -maligem Werfen eines Tetraeders beschreibt. Diese kann als binomialverteilt mit unbekanntem
-maligem Werfen eines Tetraeders beschreibt. Diese kann als binomialverteilt mit unbekanntem  und
und  betrachtet werden. Gesucht ist nun
betrachtet werden. Gesucht ist nun  sodass
sodass  gilt.
Der Tetraeder muss mindestens
gilt.
Der Tetraeder muss mindestens  mal geworfen werden, damit mit einer Wahrscheinlichkeit von mindestens
mal geworfen werden, damit mit einer Wahrscheinlichkeit von mindestens  mindestens einmal die Zahl
mindestens einmal die Zahl  geworfen wird.
geworfen wird.
c)
Wahrscheinlichkeiten berechnen
Mit den Pfadregeln folgt:
![\(\begin{array}[t]{rll}
P(C) &=& 4\cdot \dfrac{1}{4} \cdot \dfrac{1}{6} \cdot \dfrac{1}{8} \\[5pt]
&=& \dfrac{1}{48} \\[5pt]
&\approx& 0,0208 \\[5pt]
&=& 2,08\,\%
\end{array}\)](https://mathjax.schullv.de/42e30621bca463ae98648d2fe09b7a54a9df3d3186d1cb38510d473d883aadcc?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  wird mit allen drei Körpern dieselbe Zahl geworfen.
Für Ereignis
wird mit allen drei Körpern dieselbe Zahl geworfen.
Für Ereignis  gibt es folgende Möglichkeiten:
gibt es folgende Möglichkeiten:
![\(\begin{array}[t]{rll}
P(D) &=& 3\cdot \dfrac{1}{8}\cdot \dfrac{1}{6}\cdot \dfrac{1}{4} \\[5pt]
&=& \dfrac{1}{64} \\[5pt]
&\approx& 0,0156 \\[5pt]
&=& 1,56\,\% \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c6c390fd86b0817251b8d2cd0bdaf3b6d8f4b9d79fcd151d75e6ce394491d912?color=5a5a5a)
| Oktaeder | Würfel | Tetraeder | Summe |
|---|---|---|---|
| 8 | 6 | 3 | 17 |
| 8 | 5 | 4 | 17 |
| 7 | 6 | 4 | 17 |
d)
Erwartungswert für den Gewinn des Spielers bestimmen
Bezeichne mit  die Zufallsgröße, die die zufällige Anzahl der geworfenen Einsen bei dem beschriebenen Spiel beschreibt.
die Zufallsgröße, die die zufällige Anzahl der geworfenen Einsen bei dem beschriebenen Spiel beschreibt.  kann die Werte
kann die Werte 
 und
und  annehmen.
annehmen.
![\(\begin{array}[t]{rll}
P(Z=0) &=& \dfrac{3}{4}\cdot \dfrac{5}{6} \\[5pt]
&=& \dfrac{5}{8} \\[10pt]
P(Z=1) &=& \dfrac{1}{4}\cdot \dfrac{5}{6} + \dfrac{3}{4}\cdot\dfrac{1}{6} \\[5pt]
&=& \dfrac{1}{3} \\[10pt]
P(Z=2) &=& \dfrac{1}{4}\cdot \dfrac{1}{6} \\[5pt]
&=& \dfrac{1}{24}
\end{array}\)](https://mathjax.schullv.de/f60d4e401ce2175f43655985536bc02e74c5d7563bc87567b48c3627ba940c54?color=5a5a5a) Für den erwarteten Gewinn des Spielers folgt:
Der erwartete Gewinn für den Spieler beträgt
Für den erwarteten Gewinn des Spielers folgt:
Der erwartete Gewinn für den Spieler beträgt 
e)
Anzahl Tetraeder berechnen
![\(\begin{array}[t]{rll}
p&=&\dfrac{x}{20}\cdot\dfrac{1}{4}+\dfrac{20-x}{20}\cdot\dfrac{1}{8}\\[5pt]
&=&\dfrac{2x}{160}+\dfrac{20-x}{160}\\[5pt]
p&=&\dfrac{x+20}{160}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b1fd9c260f7b135a9eec3980ec3a8555400993c76f97bac841c80a0ab43f976a?color=5a5a5a) Die Wahrscheinlichkeit soll
Die Wahrscheinlichkeit soll  sein, also gilt:
sein, also gilt:
 , also
, also  und somit
und somit  Im Sack befinden sich vier Tetraeder.
Im Sack befinden sich vier Tetraeder.
