Pflichtaufgaben (P1-P4)

Die Abbildung zeigt den Graphen einer Funktion $f$ . Die Achseneinteilung der $y$ -Achse ist nicht bekannt.

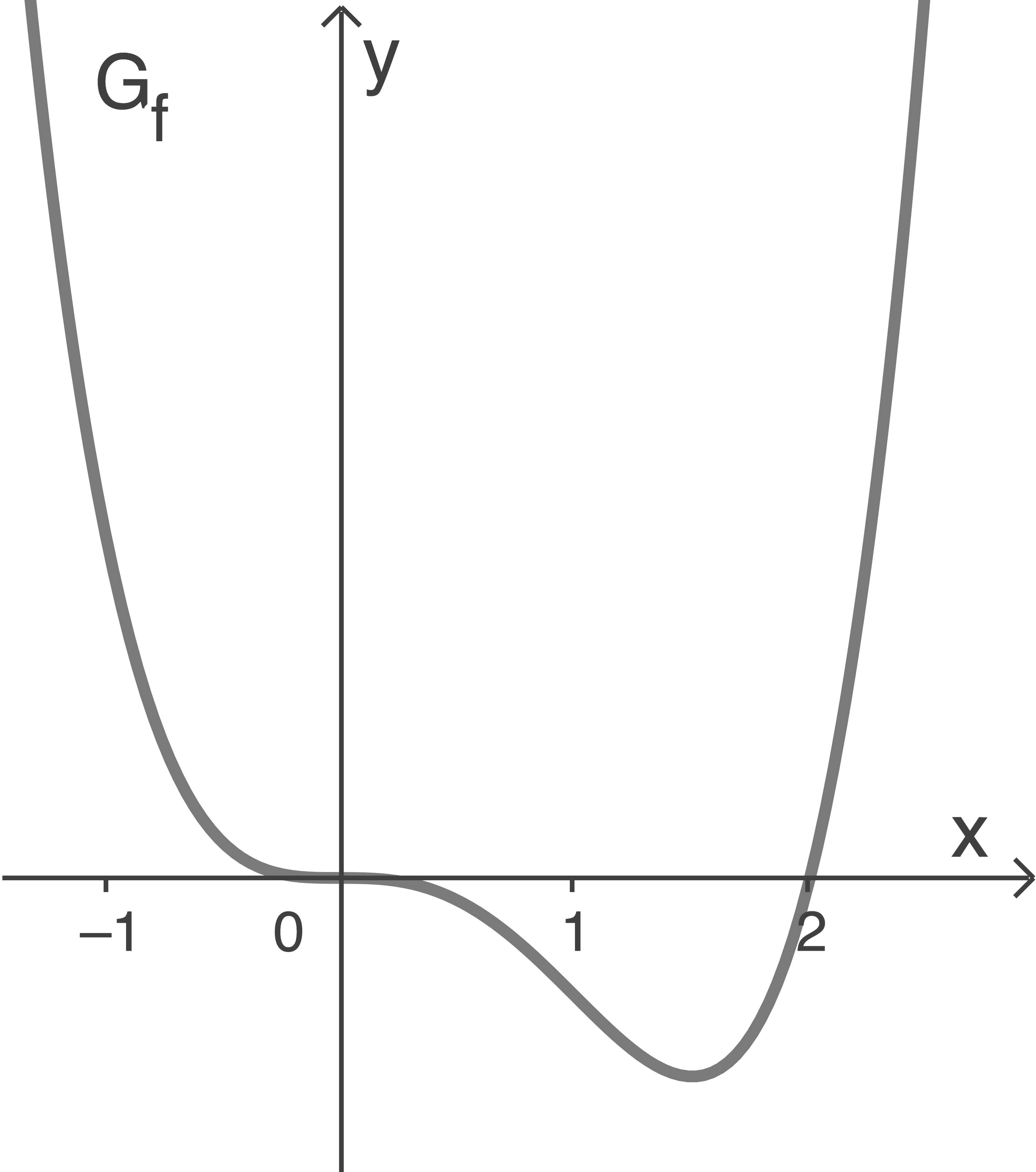
Gegeben sind die folgenden drei Funktionsgleichungen:

(I) $f_1(x)=x^2\cdot\left(x^2-4\right)$

(II) $f_2(x)=x\cdot\left(x^2-2x\right)$

(III) $f_3(x)=x^3\cdot\left(x-2\right)$

Untersuche für jede der Funktionsgleichungen (I), (II) und (III), ob sie den abgebildeten Graphen $G_f$ beschreiben kann. Begründe jeweils deine Entscheidung.

Grafik eines mathematischen Funktionsgraphen mit den Achsen x und y.

(5 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktionsschar $f_a(x)=a^2x^4+4ax^3$ ; $a \in \mathbb{R}$ ; $a>0.$

Berechne den Wert von $a,$ für den $x=-1$ eine Nullstelle von $f_a$ ist.

(1 BE)

Alle Graphen von $f_a$ haben einen von $a$ abhängigen Extrempunkt. Alle diese Extrempunkte liegen auf dem Graphen der Ortskurve $h.$ Bestimme eine Gleichung der Ortskurve $h.$

(4 BE)

Gegeben sind die Gerade $g:\overrightarrow{x}=\pmatrix{2\\1\\-1}+r\cdot\pmatrix{1\\1\\-2},$ $r\in\mathbb{R}$ und die Ebene $E: \overrightarrow{x}=\pmatrix{0\\1\\4}+s\cdot\pmatrix{4\\2\\3}+t\cdot\pmatrix{2\\0\\1},$ $s, t \in \mathbb{R}.$

Weise nach, dass die Gerade $g$ senkrecht zur Ebene $E$ verläuft.

(1 BE)

Berechne die Koordinaten des Schnittpunktes $D$ der Geraden $g$ mit der Ebene $E.$

(4 BE)

Gegeben ist eine Zufallsgröße $X,$ die die Werte $x_i \in \{0,1,2,3,4\}$ annehmen kann. Die Wahrscheinlichkeitsverteilung von $X$ ist symmetrisch.

Es gilt $P(X=2)=0,6.$
Bestimme $P(X\leq2).$

(2 BE)

Weise nach, dass die Zufallsgröße $X$ nicht binomialverteilt sein kann.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

An der Abbildung des Graphen können die Nullstellen bei $x=0$ und $x=2$ abgelesen werden.
Für $x\rightarrow\pm\infty$ gilt zudem $f(x)\to \infty.$

Die Funktion $f_1$ beschreibt den Graphen nicht, da sie eine zusätzliche Nullstelle bei $x=-2$ besitzt.

Die Funktion $f_2$ beschreibt den Graphen ebenfalls nicht, da für $x\rightarrow-\infty$ gilt $f_2(x)\to -\infty.$

Die Funktion $f_3$ kann den Graphen $G_f$ beschreiben.

$f_a(-1)=0$

$a^2\cdot (-1)^4+4a\cdot (-1)^3=0$

$a^2-4a=0$

$a(a-4)=0$

Da $a\gt 0$ , ist $a=4$ die einzige Lösung.

$\(f_a$

Notwendige Bedingung:

$\(f_a$

$4a^2x^3+12ax^2=0$

$4ax^2(ax+3)=0$

$x_1=0,$ $x_2=-\dfrac{3}{a}$

$x_1=0$ kann ausgeschlossen werden, da der Extrempunkt abhängig von $a$ sein soll.

Hinreichende Bedingung (kann auch weggelassen werden):

$\(f_a$ also liegt ein Extrempunkt vor

$f_a\left(-\dfrac{3}{a}\right)=\dfrac{81}{a^2}-\dfrac{108}{a^2}$

$x=-\dfrac{3}{a}$ nach $a$ aufgelöst ergibt $a=-\dfrac{3}{x}$

Eingesetzt in $f_a\left(-\dfrac{3}{a}\right)$ ergibt sich:

$h:y=9x^2-12x^2=-3x^2$

Orthogonalität liegt vor, wenn die Skalarprodukte des Richtungsvektors der Geraden $g$ jeweils zu beiden Spannvektoren der Ebenen $E$ gleich Null sind.

Es gilt:

$\pmatrix{1\\1\\-2}\circ \pmatrix{4\\2\\3}$ $=1\cdot4+1\cdot2+(-2)\cdot3$ $=4+2-6=0$

$\pmatrix{1\\1\\-2}\circ\pmatrix{2\\0\\1}$ $=1\cdot2+1\cdot0+(-2)\cdot1$ $=2-2=0$

Somit ist gezeigt, dass $g$ senkrecht zu $E$ verläuft.

Gleichsetzen der Geraden- und Ebenengleichung:

$\pmatrix{2\\1\\-1}+r\cdot\pmatrix{1\\1\\-2}$ $=\pmatrix{0\\1\\4}+s\cdot\pmatrix{4\\2\\3}+t\cdot\pmatrix{2\\0\\1}$

Umgeformt ergibt sich:

$r\cdot\pmatrix{1\\1\\-2}-s\cdot\pmatrix{4\\2\\3}-t\cdot\pmatrix{2\\0\\1}$ $=\pmatrix{-2\\0\\5}$

Daraus lässt sich ein LGS ableiten:

$\begin{array}{lrll} \text{I}\quad&r-4s-2t&=&-2 \\ \text{II}\quad&r-2s&=& 0\\ \text{III}\quad&-2r-3s-t&=&5 \\ \end{array}$

Aus $\text{II}$ folgt: $r=2s$

$r$ in $\text{I}$ und $\text{III}$ eingesetzt ergibt:

$\begin{array}{lrll} \text{Ia}\quad&-2s-2t&=&-2 \\ \text{IIIa}\quad&-7s-t&=&5 \\ \end{array}$

$\text{Ia}-2\text{IIIa}$ ergibt:

$12s=-12$ und damit $s=-1$

$s$ in $\text{Ia}:$ $-2\cdot(-1)-2t=-2,$ umgeformt ergibt sich:

$4=2t$ und damit $t=2$

$s$ und $t$ in $\text{I}$ : $r-4\cdot(-1)-2\cdot 2=-2$

Das ergibt $r=-2$

$r$ in $g$ eingesetzt ergibt: $\vec{x}=\pmatrix{2\\1\\-1}+(-2)\cdot\pmatrix{1\\1\\-2}=\pmatrix{2-2\\1-2\\-1+4}$ $=\pmatrix{0\\-1\\3}$

Daraus folgt der Schnittpunkt $D\left(0\mid -1\mid 3\right).$

Aus $P(X=2)$ folgt:

$P(X\leq 1) + P(X\geq 3) = 1-0,6 = 0,4$

Wegen der Symmetrie muss $P(X\leq 1) = P(X\geq3)$ sein. Also ist $P(X\leq 1) = P(X\geq3)$ $= 0,4:2 =0,2.$

Damit folgt dann:

$P(X\leq 2) = P(X\leq 1) + P(X=2)$ $= 0,2+0,6 = 0,8.$

Die Wahrscheinlichkeitsverteilung bei einer Binomialverteilung ist nur für $p=\frac{1}{2}$ symmetrisch. Wäre $X$ mit $n=4$ und $p=\frac{1}{2}$ binomialverteilt, ergäben sich folgende Wahrscheinlichkeiten:

$P(X=0) = \left(\frac{1}{2}\right)^4 = \frac{1}{16}$

$P(X=1)= \pmatrix{4\\1} \cdot \frac{1}{2}\cdot \left(\frac{1}{2}\right)^3$ $= 4\cdot \frac{1}{16} = \frac{1}{4}$

$P(X\leq 1) = \frac{1}{16} + \frac{1}{4}$ $= \frac{5}{16} \neq 0,2$

Die Wahrscheinlichkeiten widersprechen also den Ergebnissen aus Teilaufgabe a). $X$ kann daher nicht binomialverteilt sein.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?