Wahlteil B2

In einem Klassenzimmer befindet sich eine rechteckige Projektionsfläche. Ihre Eckpunkte werden in einem Koordinatensystem durch die Punkte $A\,(0 \mid 4,4 \mid 1)$ , $B\,(1\mid 6,8 \mid 1)$ , $C\,(1 \mid 6,8\mid 2,6)$ , und $D\,(0\mid 4,4 \mid 2,6)$ dargestellt (alle Koordinatenangaben in Meter). Die Klassenzimmerwand hinter der Projektionsfläche liegt in einer Ebene, die durch die $x_2x_3$ -Ebene beschrieben wird.

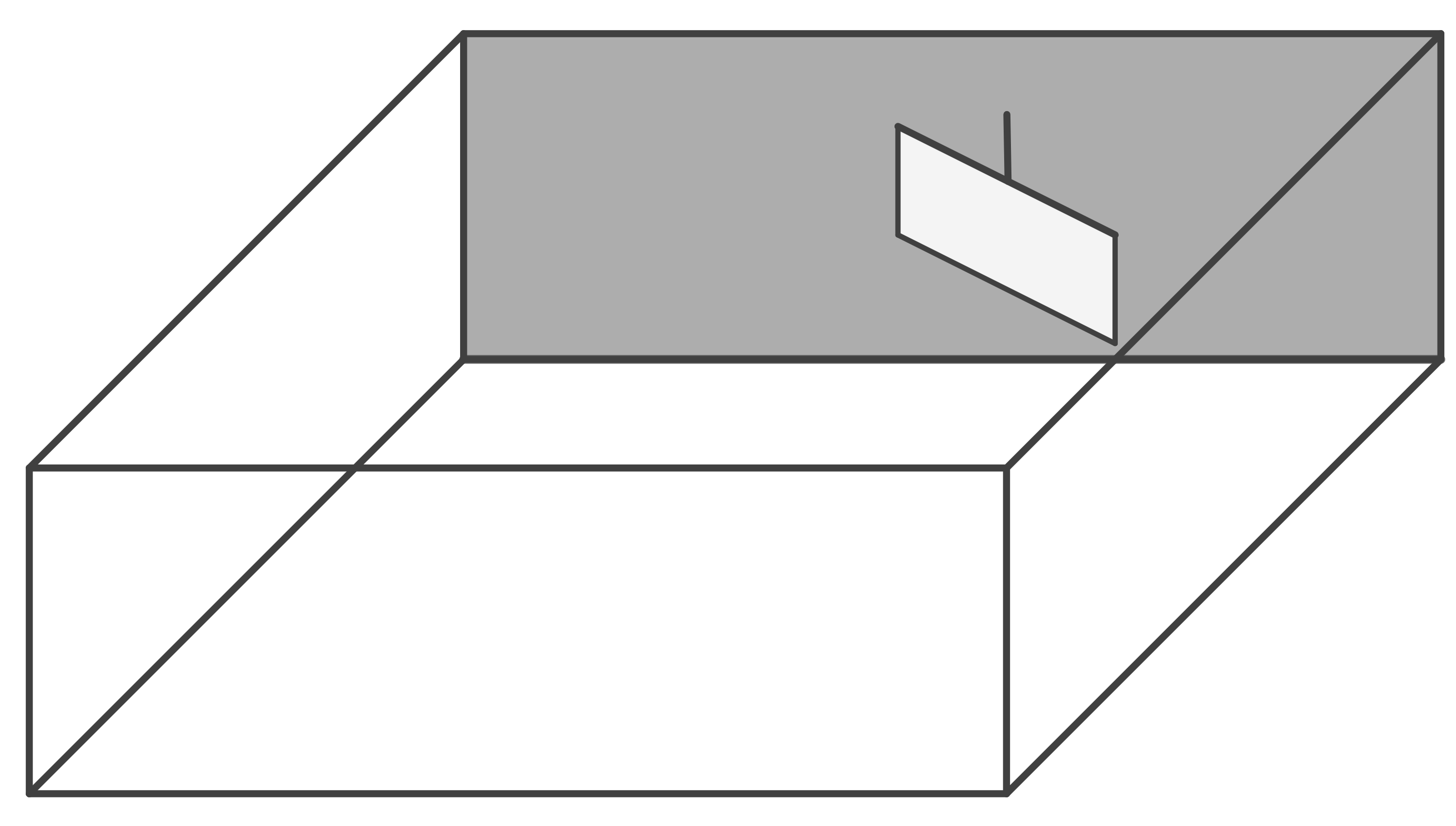
Grafische Darstellung eines dreidimensionalen Objekts mit verschiedenen Flächen und Linien.

Skizze nicht maßstäblich

Berechne die Länge der Diagonalen der Projektionsfläche.
Die Punkte $A$ , $B$ , $C$ und $D$ liegen in einer Ebene $E.$
Bestimme die Koordinatengleichung von $E$ .
Berechne die Weite des Winkels, den die Projektionsfläche und die dahinter liegende Wand des Klassenzimmers einschließen.
(Teilergebnis: $E: 12x_1-5x_2=-22$ )

(4 VP)

Ein Schüler zielt mit einem Laserpointer auf die Projektionsfläche. Die Lichtquelle wird im Modell durch den Punkt $L\,(4\mid 2 \mid 1)$ dargestellt, der Vektor $\overrightarrow{v}=$ $\pmatrix{-5\\6\\2}$ beschreibt die Richtung des Laserstrahls.
Überprüfe, ob der Laserstrahl die Projektionsfläche trifft.

(2,5 VP)

Die Projektionsfläche ist so befestigt, dass sie sich um eine vertikale Achse drehen lässt. Im Modell lassen sich mögliche Lagen der Projektionsfläche durch Ebenen der Schar $E_a : 12x_1+5ax_2=28a+6$ ; $a \in \mathbb{R}$ beschreiben.

Weise nach, dass der Mittelpunkt der Strecke $\overline{CD}$ in jeder Ebene der Schar liegt.
Die Drehachse wird im Modell durch eine Strecke beschrieben.
Gib eine Gleichung der Geraden an, die diese Strecke enthält.

(1,5 VP)

Begründe, dass die Ebene $E_1$ eine Lage beschreibt, in der die Projektionsfläche an der dahinterliegenden Wand anstößt.

(2 VP)

Länge der Diagonalen berechnen
Die Diagonale entspricht der Strecke $\overline{AC}$ .

Vollständigen Rechenweg anzeigen

Die Länge der Diagonalen beträgt etwa $3,05\,\text{m}.$

Koordinatengleichung der Ebene $E$ aufstellen

$\overrightarrow{AB} = \pmatrix{1\\6,8\\1} - \pmatrix{0\\4,4\\1} = \pmatrix{1\\2,4\\0}$

$\overrightarrow{AD} = \pmatrix{0\\4,4\\2,6} -\pmatrix{0\\4,4\\1} = \pmatrix{0\\0\\1,6}$

Normalenvektor $\overrightarrow{n}$ von $E$ bestimmen:

$\overrightarrow{AB}\cdot\overrightarrow{n}=0$ und $\overrightarrow{AD}\cdot\overrightarrow{n}=0$ , daraus folgt ein LGS:

$\begin{array}{lrll} \text{I}\quad&n_1+2,4n_2&=& 0 \\ \text{II}\quad&1,6n_3&=&0 \\ \end{array}$

Für z.B. $n_1=12$ folgt $n_2=-5$ und $n_3=0.$

$\overrightarrow{n}= \pmatrix{12\\-5\\0}$

Daraus folgt: $E: 12x_1 -5x_2 =c$ .

Einsetzen des Punktes $B(1\mid 6,8\mid 1)$ ergibt $c:$

$12\cdot 1 -5\cdot 6,8 =c=-22$

Somit lautet eine mögliche Ebenengleichung $E:12x_1-5x_2=-22.$

Winkel berechnen

Die Wand des Klassenzimmers liegt in der $x_2x_3$ -Ebene. Diese hat den Normalenvektor $\pmatrix{1\\0\\0}$ . Damit lässt sich der Winkel berechnen:

$\cos(\alpha)= \dfrac{\left |\pmatrix{1\\0\\0} \cdot \pmatrix{12\\-5\\0}\right |}{\left | \pmatrix{1\\0\\0}\right | \cdot \left | \pmatrix{12\\-5\\0}\right |} =\dfrac{12}{13}$

$\alpha \approx 22,6°$

Überprüfen, ob die Projektionsfläche getroffen wird

Zunächst wird die Gleichung der Geraden aufgestellt, auf welcher der Laserstrahl liegt: $g: \overrightarrow{x}= \overrightarrow{OL} + s \cdot \overrightarrow{v}$ , also $g: \overrightarrow{x}= \pmatrix{4\\2\\1} + s \cdot \pmatrix{-5\\6\\2}$ .
Schnittpunkt von $g$ und $E$ berechnen:
$x_1=4-5s$ und $x_2=2+6s$ aus $g$ werden dafür in die Koordinatengleichung von $E$ eingesetzt.

$\begin{array}[t]{rll} 12(4-5s)-5(2+6s)&=&-22 &\quad \scriptsize \\[5pt] 48-60s-10-30s&=&-22 \\[5pt] -60s+38&=&-22 \quad \scriptsize \mid\; -38 \\[5pt] -90s&=&-60 \quad \scriptsize \mid\; :(-90) \\[5pt] s&=&\dfrac{2}{3} \end{array}$

$s$ in $g$ eingesetzt ergibt: $\overrightarrow{OS}= \pmatrix{4\\2\\1} +\dfrac{2}{3} \cdot \pmatrix{-5\\6\\2} = \pmatrix{\frac{2}{3} \\6 \\ \frac{7}{3} }$

Überprüfung, ob $S$ in der Ebene liegt:

$\begin{array}[t]{rll} 12 \cdot \dfrac{2}{3} -5 \cdot 6&=&-22 &\quad \scriptsize \\[5pt] -22&=&-22 \end{array}$

Die Projektionsfläche ist rechteckig, also müssen die Koordinaten des Punktes $S$ mit den Eckpunkten der projektionsfläche verglichen werden: Wegen $0 \lt \dfrac{2}{3} \lt 1,$ $4,4 \lt 6 \lt 6,8$ und $1\lt \dfrac{7}{3} \lt 2,6$ liegt der Punkt S innerhalb der Projektionsfläche.

Damit liegt $S$ in der Ebene $E$ und der Laserpointer trifft die Projektionsfläche.

Nachweisen, dass der Mittelpunkt in jeder Ebene der Schar liegt
Den Mittelpunkt kann man wie folgt ermitteln:

$\overrightarrow{0M}= \pmatrix{0,5\\5,6\\2,6}$

Vollständige Lösung anzeigen

$M$ in $E_a$ eingesetzt:

$\begin{array}[t]{rll} 12 \cdot 0,5 + 5a \cdot 5,6&=&28 a+6 &\quad \scriptsize \\[5pt] 6 + 28a &=&28 a+6 &\quad \scriptsize \\[5pt] \end{array}$

Damit ist die Aussage wahr für alle $a\in\mathbb{R}$ .

Gleichung der Geraden angeben
Die Drehachse ist senkrecht zum Boden und hat somit den Richtungsvektor $\pmatrix{0\\0\\1}$ .
Die Gleichung der Geraden ergibt sich aus dem Mittelpunkt (der in jeder Ebene $E_a$ enthalten ist) und der Richtung der Drehachse:

$h: \overrightarrow{x}= \pmatrix{0,5\\5,6\\2,6} +t \cdot \pmatrix{0\\0\\1}$

Begründen
Ein Schnitt der Ebene $E_1$ mit der $x_2x_3$ -Ebene führt zum LGS

$\begin{array}[t]{rll} 12x_1 +5x_2&=&34 &\quad \scriptsize \\[5pt] x_1&=&0 \end{array}$

mit den Lösungen $(0; \, 6,8; \, t)$ .

Für $t=2,6$ liegt der Punkt $P(0 \mid 6,8 \mid 2,6)$ auf der Schnittgeraden und hat dieselbe $x_3$ -Koordinate wie der Punkt $M.$

Wegen $\left|\overrightarrow{MP}\right|= \sqrt{(-0,5)^2 +(6,8-5,6)^2} = 1,3$ und $\left|\overrightarrow{MC}\right|= \sqrt{0,5^2 +(6,8-5,6)^2} =1,3$ stellt $P$ die rechte obere Ecke der gedrehten Projektionsfläche dar, woraus folgt, dass diese an der Wand anstößt.