Lerninhalte in Mathe

Abi-Aufgaben

Digitales Schulbuch

Inhaltsverzeichnis

Wahlteil B1

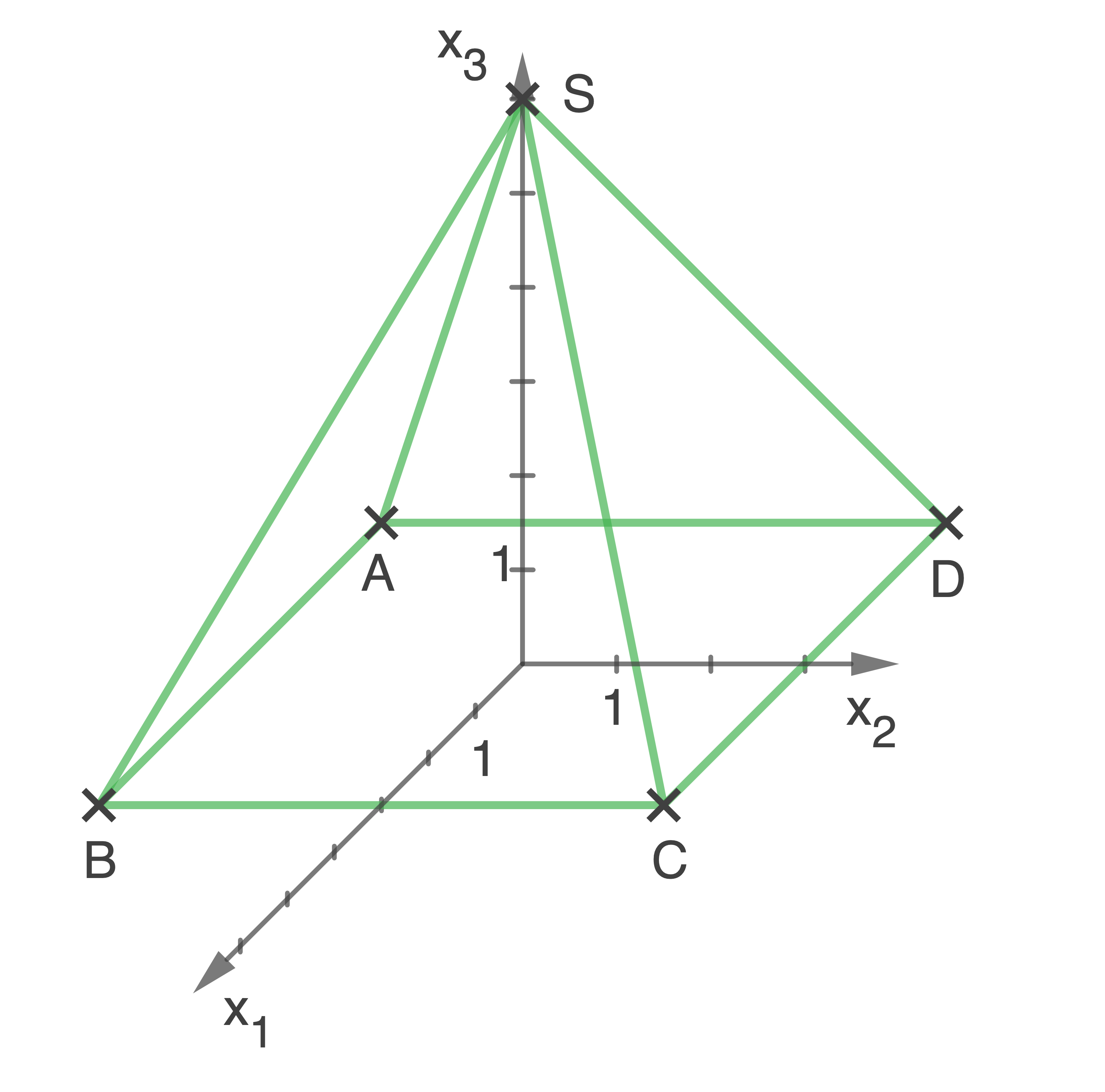
Gegeben ist eine gerade Pyramide mit quadratischer Grundfläche.
Die Eckpunkte der Grundfläche sind $A(-3\mid -3 \mid 0), B(3\mid -3\mid 0), C(3\mid 3 \mid 0)$ und $D,$
die Spitze ist $S(0\mid 0\mid 6).$
Die Ebene $E$ enthält die Punkte $A, B$ und $S.$

a)

Stelle die Pyramide in einem geeigneten Koordinatensystem dar.

(1 VP)

Bestimme eine Koordinatengleichung der Ebene $E.$

(2 VP)

Berechne den Oberflächeninhalt der Pyramide.
(Teilergebnis: $E: 2x_2-x_3=-6$ )

(2 VP)

b)

Innerhalb der Pyramide gibt es einen Punkt, dessen Abstand von der Grundfläche der Pyramide $\sqrt{5}$ -mal so groß ist wie sein Abstand zu den Seitenflächen.
Berechne die Koordinaten dieses Punktes.

(2,5 VP)

c)

Betrachtet wird für jedes $a\gt 0$ die gerade Pyramide mit folgenden Eigenschaften:

$A(-a\mid -a\mid 0),$ $B(a\mid -a\mid 0),$ $C(a\mid a\mid 0)$ und $D$ sind die Eckpunkte der quadratischen Grundfläche.
Die $x_3-$ Koordinate der Spitze $S$ ist positiv.
Die Höhe der Pyramide stimmt mit der Kantenlänge der Grundfläche überein.

$M_1$ ist die Kantenmitte von $AB,$ $M_2$ die Kantenmitte von $DS.$
Zeige: Die Strecke $M_1M_2$ ist orthogonal zur Kante $DS.$

(2,5 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?