Wahlteil A1
Aufgabe A1
Der Laderaum eines Lastkahns ist  lang. Sein Querschnitt ist auf der gesamten Länge gleich und wird modellhaft beschrieben durch den Graphen der Funktion
lang. Sein Querschnitt ist auf der gesamten Länge gleich und wird modellhaft beschrieben durch den Graphen der Funktion  mit
mit
 (
( und
und  in Meter).
in Meter).
a)
Wie tief ist der Laderaum in der Mitte?
Wie breit ist er in Höhe?
Höhe?
In welchem Bereich hat der Boden des Laderaums eine Neigung unter 5%.
Berechne das Volumen des Laderaums.
Wie breit ist er in
In welchem Bereich hat der Boden des Laderaums eine Neigung unter 5%.
Berechne das Volumen des Laderaums.
(5 VP)
b)
Zur Wartung steht der Lastkahn an Land auf einer ebenen Plattform. Dort wird er stabilisiert durch gerade Stützen, die orthogonal zur Au?enwand des Laderaums angebracht sind. Betrachtet werden zwei einander gegenüberliegende Stützen, deren Befestigungspunkte im Modell durch die Punkte
 und
und  beschrieben werden.
beschrieben werden.
In welchem Abstand voneinander enden diese Stützen auf der Plattform?
In welchem Abstand voneinander enden diese Stützen auf der Plattform?
(3 VP)
c)
Der Laderaum kann durch eine horizontale Zwischendecke der Länge  in zwei Teilräume geteilt werden. Das Volumen des unteren Teilraums beträgt
in zwei Teilräume geteilt werden. Das Volumen des unteren Teilraums beträgt 
Berechne die Breite der Zwischendecke.
Berechne die Breite der Zwischendecke.
(4 VP)
d)
Untersuche, ob sich eine zylinderförmige Röhre mit Au?endurchmesser  so in Längsrichtung in den Laderaum legen lässt, dass sie ihn an der tiefsten Stelle berührt.
so in Längsrichtung in den Laderaum legen lässt, dass sie ihn an der tiefsten Stelle berührt.
(3 VP)
a)
Bestimmen der Tiefe des Laderaums in der Mitte
Der Aufgabenstellung kannst du hier entnehmen, dass der Querschnitt des Laderaums eines Lastkahns modellhaft durch die Funktion  beschrieben werden kann:
beschrieben werden kann:
 für
für  Willst du nun bestimmen, wie tief der Laderaum in der Mitte ist, so betrachte den Definitionsbereich der Funktion
Willst du nun bestimmen, wie tief der Laderaum in der Mitte ist, so betrachte den Definitionsbereich der Funktion  .
Da mit
.
Da mit  ein symmetrischer Definitionsbereich gegeben ist und da
ein symmetrischer Definitionsbereich gegeben ist und da  eine Funktion mit geraden Exponent ist, liegt die Mitte des Laderaums folglich an der Stelle
eine Funktion mit geraden Exponent ist, liegt die Mitte des Laderaums folglich an der Stelle  . Um die Tiefe zu bestimmen, musst du die Differenz zwischen den Funktionswerten von
. Um die Tiefe zu bestimmen, musst du die Differenz zwischen den Funktionswerten von  an den Stelle
an den Stelle  und
und  oder
oder  betrachten.
betrachten.
![\(\begin{array}[t]{rll}
f(x_M = 0)&=& \dfrac{1}{125} \cdot 0^4 = 0
\end{array}\)](https://mathjax.schullv.de/c10e893b984dd5f54384fb7b5aad7fe297a78836be90ab7d617b3a1bad183b5f?color=5a5a5a)
![\(\begin{array}[t]{rll}
f(x_M = 5)&=& \dfrac{1}{125} \cdot 5^4 = 5
\end{array}\)](https://mathjax.schullv.de/fba242ddea5fd8dff04b48011b99e2b1ec2b759ef08edb974c3aa9e04ddb85fc?color=5a5a5a) Die Differenz zwischen den Funktionswerten beträgt 5. Daraus folgt, dass der Laderaum in der Mitte eine Tiefe von 5 m besitzt.
Bestimmen der Breite des Laderaums in 3 m Höhe
Nun sollst du die Breite des Laderaums in 3 m Höhe bestimmen. Da
Die Differenz zwischen den Funktionswerten beträgt 5. Daraus folgt, dass der Laderaum in der Mitte eine Tiefe von 5 m besitzt.
Bestimmen der Breite des Laderaums in 3 m Höhe
Nun sollst du die Breite des Laderaums in 3 m Höhe bestimmen. Da  gilt, bedeutet das, dass du die
gilt, bedeutet das, dass du die  -Koordinaten zu
-Koordinaten zu  und
und  berechnen musst, um anhand dieser dann die Breite des Laderaums zu bestimmen.
berechnen musst, um anhand dieser dann die Breite des Laderaums zu bestimmen.
Da es sich bei um eine gerade Funktion handelt und da für diese
um eine gerade Funktion handelt und da für diese  gilt, ist es ausreichend den Funktionswert an einer dieser Stellen zu berechnen, um die Breite zu bestimmen.
gilt, ist es ausreichend den Funktionswert an einer dieser Stellen zu berechnen, um die Breite zu bestimmen.
![\(\begin{array}[t]{rll}
f(x_1) = 3&=& \dfrac{1}{125} \cdot x^4 \quad \scriptsize \mid\; \cdot 125\\[5pt]
-375&=&x^4 \quad \scriptsize \mid\; \sqrt[4]{\,}\\[5pt]
4,4&=&x
\end{array}\)](https://mathjax.schullv.de/c89074a1ca6001c40af5ac919efeea9747d2441ba15b9456a0a8c733f1d2d1fe?color=5a5a5a) Die Breite des Laderaums in 3 m Höhe beträgt also
Die Breite des Laderaums in 3 m Höhe beträgt also  Bestimmen des Bereichs mit einer Neigung unter 5 %
Hier ist der Bereich gesucht, in dem der Boden des Laderaums eine Neigung unter 5 % besitzt.
Bestimmen des Bereichs mit einer Neigung unter 5 %
Hier ist der Bereich gesucht, in dem der Boden des Laderaums eine Neigung unter 5 % besitzt.
Beachte hierbei, dass die Neigung des Laderaums durch die erste Ableitung der Funktion beschrieben werden kann. Diese gibt zu jeder Stelle
beschrieben werden kann. Diese gibt zu jeder Stelle  die Steigung der Funktion
die Steigung der Funktion  an und folglich bestimmt diese die Neigung des Rumpfes.
an und folglich bestimmt diese die Neigung des Rumpfes.
Willst du diese Aufgabe lösen, so bestimme zuerst die Stellen, an welchen die Neigung gleich 5 % ist. An diesen Stellen muss dann gelten:
 Bestimme dann mit diesen Stellen den gesuchten Bereich.
1. Schritt: Bestimmen der Ableitung von
Bestimme dann mit diesen Stellen den gesuchten Bereich.
1. Schritt: Bestimmen der Ableitung von  Die erste Ableitung von
Die erste Ableitung von  kannst du hier mittels Faktorregel bestimmen.
kannst du hier mittels Faktorregel bestimmen.
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{125} \cdot x^4 \\[5pt]
f‘(x)&=& \dfrac{4}{125} \cdot x^3
\end{array}\)](https://mathjax.schullv.de/f28f59f6db174658dd761e29806d07f25bcda75222c282b311650e40f0d5ad69?color=5a5a5a) 2. Schritt: Bestimmen der Stellen mit einer Neigung von 5 %
Setze nun den Funktionsterm von
2. Schritt: Bestimmen der Stellen mit einer Neigung von 5 %
Setze nun den Funktionsterm von  mit 0,05 gleich, um die Stellen mit einem Anstieg von 5 % zu bestimmen:
mit 0,05 gleich, um die Stellen mit einem Anstieg von 5 % zu bestimmen:
![\(\begin{array}[t]{rll}
f‘(x)&=& 0,05 \\[5pt]
0,05&=& \dfrac{4}{125} \cdot x^3 \quad \scriptsize \mid\; \cdot \dfrac{125}{4}\\[5pt]
1,5625&=& x^3 \quad \scriptsize \mid\; \sqrt[3]{\;}\\[5pt]
1,16&=& x
\end{array}\)](https://mathjax.schullv.de/c03cff72c20f07b72a78207c175b208a3b8f0d0ab952c92656d59e5788a036ee?color=5a5a5a) Aufgrund der Symmetrie und der oben beschrieben Eigenschaften des Graphen von
Aufgrund der Symmetrie und der oben beschrieben Eigenschaften des Graphen von  ergibt sich hier, dass der Laderaum bis zu 1,16 m links und 1,16 m rechts von der Mitte eine Neigung besitzt, die kleiner als 5 % ist.
Berechnen des Volumens des Laderaums
Der Querschnitt des Laderaums ist auf der gesamten Länge gleich und wird durch den Graphen der Funktion
ergibt sich hier, dass der Laderaum bis zu 1,16 m links und 1,16 m rechts von der Mitte eine Neigung besitzt, die kleiner als 5 % ist.
Berechnen des Volumens des Laderaums
Der Querschnitt des Laderaums ist auf der gesamten Länge gleich und wird durch den Graphen der Funktion  beschrieben. Weiterhin kannst du der Aufgabenstellung entnehmen, dass der Laderaum des Lastkahns eine Länge von 50 m besitzt.
beschrieben. Weiterhin kannst du der Aufgabenstellung entnehmen, dass der Laderaum des Lastkahns eine Länge von 50 m besitzt.
Deine Aufgabe ist es nun das Volumen des Laderaums zu berechnen. Beim Laderaum handelt es sich also um einen Körper. Dieser Körper besitzt eine Grundfläche , in Form des Querschnitts des Laderaums und eine Länge von
, in Form des Querschnitts des Laderaums und eine Länge von  . Das Volumen berechnet sich dann über folgende Formel:
. Das Volumen berechnet sich dann über folgende Formel:
 Gehe wie folgt vor, um das Volumen
Gehe wie folgt vor, um das Volumen  des Laderaums zu berechnen:
des Laderaums zu berechnen:
 Der Querschnitt des Laderaums wird über den Graphen von
Der Querschnitt des Laderaums wird über den Graphen von  im Bereich
im Bereich  beschrieben. Betrachte vor dem Integrieren den Graphen der Funktion
beschrieben. Betrachte vor dem Integrieren den Graphen der Funktion  im GRAPH Modus deines GTR:
im GRAPH Modus deines GTR:
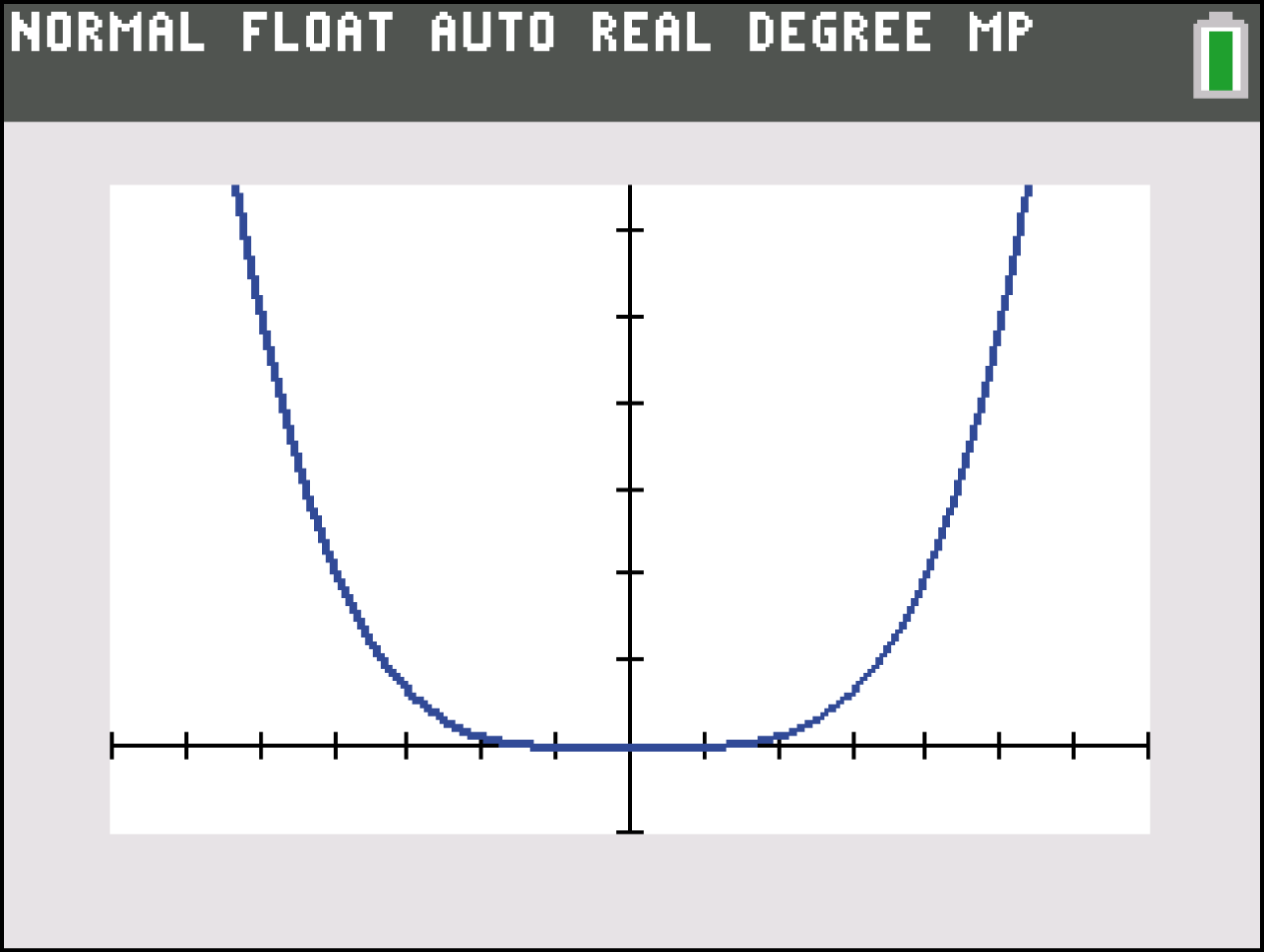 Oben kannst du sehen, dass sich der Graph von
Oben kannst du sehen, dass sich der Graph von  im betrachteten Bereich oberhalb der
im betrachteten Bereich oberhalb der  -Achse befindet. Möchtest du nun die Querschnittsfläche berechnen, so berechne zunächst die Fläche eines Rechtecks mit der Höhe und der Breite des Querschnitts und subtrahiere von dieser dann das Integral über
-Achse befindet. Möchtest du nun die Querschnittsfläche berechnen, so berechne zunächst die Fläche eines Rechtecks mit der Höhe und der Breite des Querschnitts und subtrahiere von dieser dann das Integral über  im Bereich
im Bereich  und
und  .
.
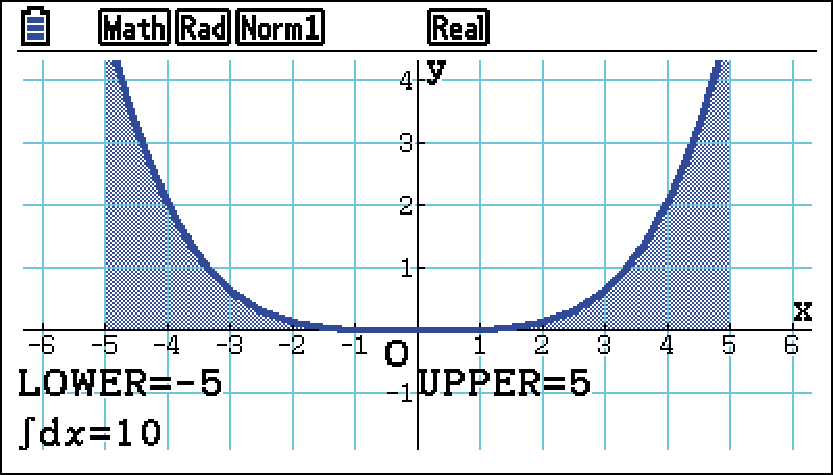
Das Integral über im betrachteten Bereich kannst du ebenfalls im GRAPH deines GTR berechnen:
im betrachteten Bereich kannst du ebenfalls im GRAPH deines GTR berechnen:
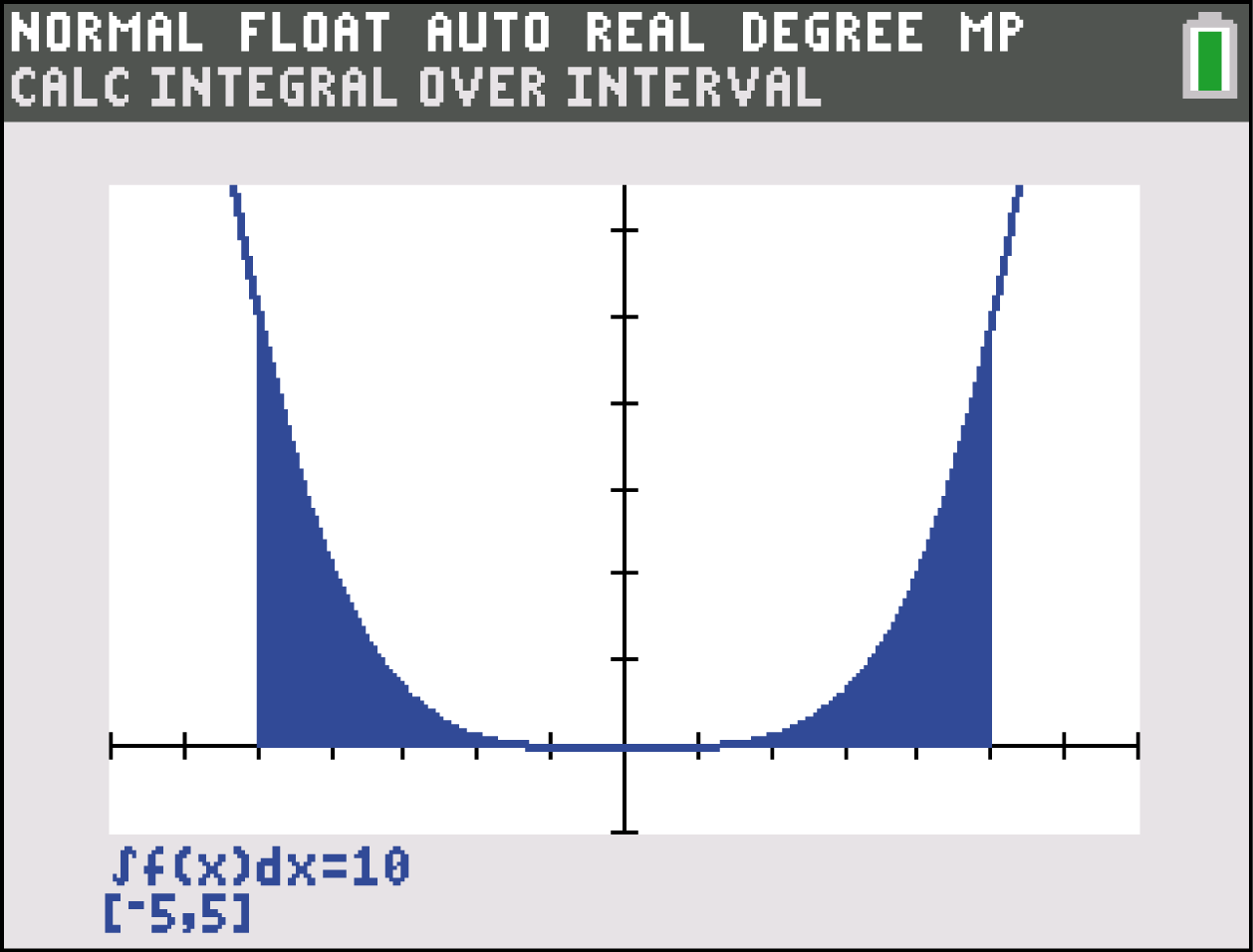 Willst du nun den Flächeninhalt
Willst du nun den Flächeninhalt  der Querschnittsfläche berechnen, so subtrahiere vom Flächeninhalt des oben beschriebenen Rechtecks die berechneten 10
der Querschnittsfläche berechnen, so subtrahiere vom Flächeninhalt des oben beschriebenen Rechtecks die berechneten 10  ;
;

 2. Schritt: Berechnen des Volumens
2. Schritt: Berechnen des Volumens  Setze
Setze  und
und  in die Volumenformel ein, um das gesuchte
in die Volumenformel ein, um das gesuchte  zu berechnen:
zu berechnen:
![\(\begin{array}[t]{rll}
V&=&40\,\text{m}^2 \cdot 50\,\text{m} = 2.000\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/8afb2c333992a6164a517dbd239a728267d07e622c62a5b793e45a290a46519d?color=5a5a5a) Der Laderaum besitzt ein Volumen von
Der Laderaum besitzt ein Volumen von  .
.
Da es sich bei
Beachte hierbei, dass die Neigung des Laderaums durch die erste Ableitung der Funktion
Willst du diese Aufgabe lösen, so bestimme zuerst die Stellen, an welchen die Neigung gleich 5 % ist. An diesen Stellen muss dann gelten:
Deine Aufgabe ist es nun das Volumen des Laderaums zu berechnen. Beim Laderaum handelt es sich also um einen Körper. Dieser Körper besitzt eine Grundfläche
- Berechne den Flächeninhalt des Querschnitts. Verwende hierzu ein Integral und deinen GTR
- Setze
und
in die Volumenformel ein und berechne das Volumen

Das Integral über
2nd  CALC
CALC  7:
7: f(x)dx
f(x)dx
Mit dem GTR folgt:

b)
Berechnen des Abstands der Stützen zueinander
Der Lastkahn steht zur Wartung auf einer ebenen Plattform an Land. Dort wird er durch gerade Stützen stabilisiert, die orthogonal zur Außenwand angebracht sind. Die Befestigungspunkte dieser Stützen sind:
Willst du den Abstand berechnen, so musst du zunächst die Stützen durch Geraden beschreiben und über den Schnittpunkt dieser mit der -Achse den gesuchten Abstand berechnen.
-Achse den gesuchten Abstand berechnen.
Gehe dabei so vor: zur Stütze zu
zur Stütze zu  Dir ist bekannt, dass die Stütze am Punkt
Dir ist bekannt, dass die Stütze am Punkt  orthogonal zur Außenwand verläuft. Daraus folgt, dass die gesuchte Gerade
orthogonal zur Außenwand verläuft. Daraus folgt, dass die gesuchte Gerade  der Normalen an den Graphen von
der Normalen an den Graphen von  im Punkt
im Punkt  entspricht.
entspricht.
Die Steigung von
von  kannst du mit diesem Zusammenhang
kannst du mit diesem Zusammenhang
 und der Ableitung
und der Ableitung  von
von  berechnen:
Den
berechnen:
Den  -Achsenabschnitt der Geraden
-Achsenabschnitt der Geraden  berechnest du über eine Punktprobe mit dem Punkt
berechnest du über eine Punktprobe mit dem Punkt  :
Gerade
:
Gerade  ergibt sich also zu:
ergibt sich also zu:  2. Schritt: Bestimmen des Schnittpunkts der Geraden
2. Schritt: Bestimmen des Schnittpunkts der Geraden  mit der
mit der  -Achse
Den Schnittpunkt von
-Achse
Den Schnittpunkt von  mit der
mit der  - Achse bestimmst du, indem du den Funktionsterm von
- Achse bestimmst du, indem du den Funktionsterm von  mit gleich Null setzt und die Gleichung nach
mit gleich Null setzt und die Gleichung nach  auflöst:
auflöst:
 schneidet also bei
schneidet also bei  die
die  -Achse. Beachte wieder die Symmetrie des Graphen von
-Achse. Beachte wieder die Symmetrie des Graphen von  um den Abstand
um den Abstand  zwischen den Stützen zu berechnen:
zwischen den Stützen zu berechnen:
![\(\begin{array}[t]{rll}
d&=& 2 \cdot \left|-8,16\right| = 16,32 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b3ab868dd1fbde94880ee1c72545c6af5cd94a338b59334ca0f4081e2853a289?color=5a5a5a) Der Abstand zwischen den zwei Stützen ist 16,32 m
Der Abstand zwischen den zwei Stützen ist 16,32 m
Willst du den Abstand berechnen, so musst du zunächst die Stützen durch Geraden beschreiben und über den Schnittpunkt dieser mit der
Gehe dabei so vor:
- Bestimme die Steigung der Geraden der Stütze zu
über die Steigung der zugehörigen Normalen
- Ermittle den
-Achsenabschnitt über eine Punktprobe
- Bestimme die Schnittstelle mit der
-Achse und bestimme mittels der Symmetrie des Graphen von
den gesuchten Abstand
Die Steigung
c)
Berechnen der Breite der Zwischendecke
Der Laderaum kann durch eine horizontale Zwischendecke der Länge 50 m in zwei Teilräume geteilt werden. Das Volumen des unteren Teilraums beträgt dann 500  .
.
Deine Aufgabe ist es nun, die Breite der Zwischendecke zu berechnen. Fertige dir dazu zunächst eine Skizze an:
der Zwischendecke zu berechnen. Fertige dir dazu zunächst eine Skizze an:
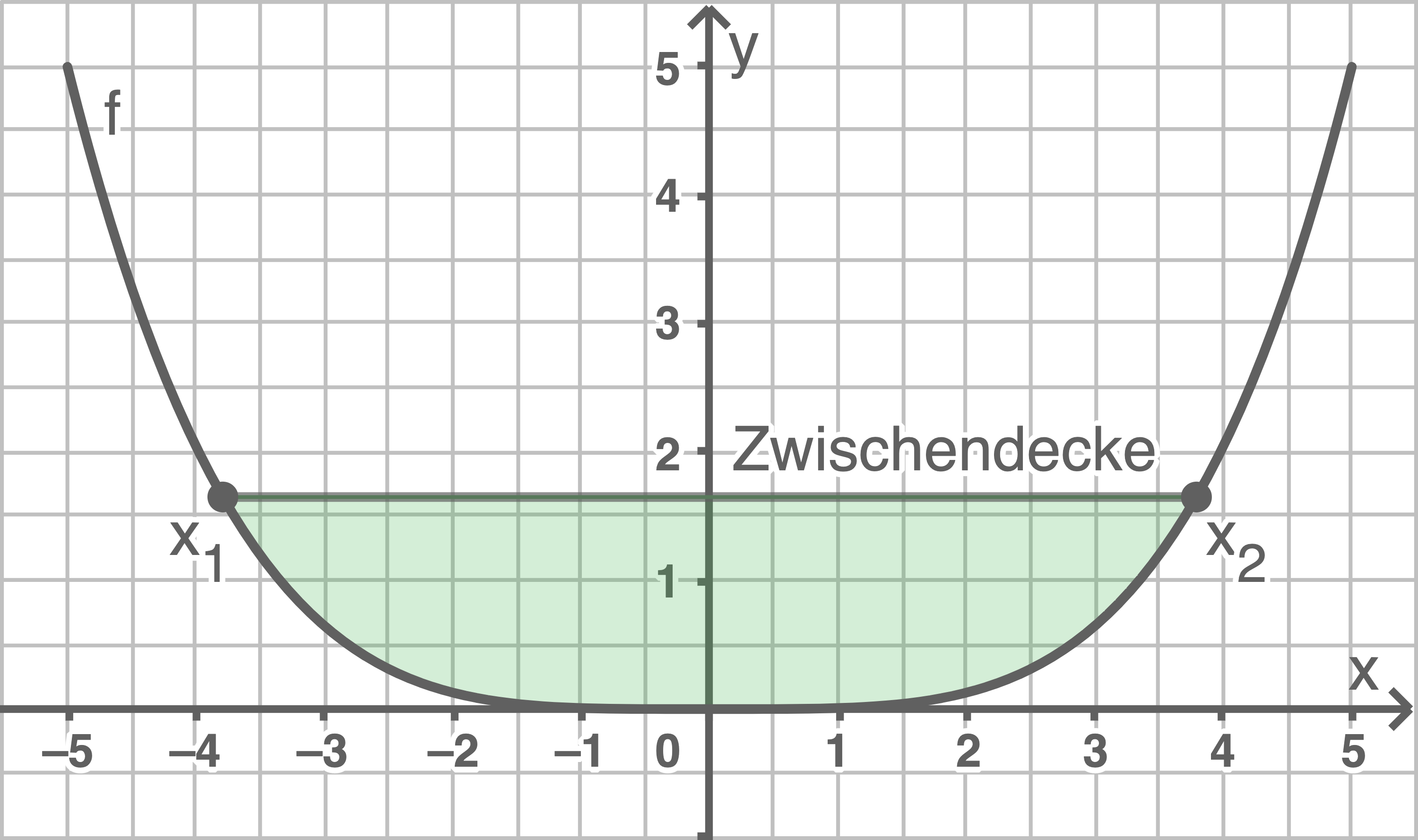 Willst du diese Aufgabe lösen, so musst du hier mit einem Integral arbeiten. Dabei ist es vorteilhaft nur einen Teil der gesamten Fläche zu betrachten, denn diese lässt sich in zwei gleich große Flächenstücke zerteilen.
Willst du diese Aufgabe lösen, so musst du hier mit einem Integral arbeiten. Dabei ist es vorteilhaft nur einen Teil der gesamten Fläche zu betrachten, denn diese lässt sich in zwei gleich große Flächenstücke zerteilen.
Willst du die Breite der Zwischendecke berechnen, so dir bekannt sein, an welcher Stelle
der Zwischendecke berechnen, so dir bekannt sein, an welcher Stelle  diese am Graphen der Funktion
diese am Graphen der Funktion  anliegt. Gehe dazu so vor:
anliegt. Gehe dazu so vor:
 Willst du berechnen, welchen Flächeninhalt
Willst du berechnen, welchen Flächeninhalt  die Zwischendecke mit dem Graphen von
die Zwischendecke mit dem Graphen von  einschließt, so setze
einschließt, so setze  und
und  in die Volumenformel aus der Teilaufgabe a ein:
in die Volumenformel aus der Teilaufgabe a ein:
![\(\begin{array}[t]{rll}
V&=&A \cdot l \quad \scriptsize \mid\;: l \\[5pt]
A&=&\dfrac{500\,\text{m}^3}{50\,\text{m}} = 10\,\text{m}^2\\[5pt]
\end{array}\)](https://mathjax.schullv.de/7ab1b70385951c78c76ab4d71d80d3d30d728f684c5357fa4256354ede1a4c85?color=5a5a5a) Der Flächeninhalt des betrachteten halben Flächenstücks ist also:
Der Flächeninhalt des betrachteten halben Flächenstücks ist also:  2. Schritt: Bestimmen der gesuchten Breite
Analog zum Aufgabenteil a berechnet sich der Flächeninhalt der halben Fläche über eine Rechteckfläche und ein Integral über den Graphen von
2. Schritt: Bestimmen der gesuchten Breite
Analog zum Aufgabenteil a berechnet sich der Flächeninhalt der halben Fläche über eine Rechteckfläche und ein Integral über den Graphen von  . Das hier betrachtete Rechteck besitzt dabei die Länge
. Das hier betrachtete Rechteck besitzt dabei die Länge  und die Höhe
und die Höhe  . Das Integral über
. Das Integral über  folglich die Grenzen 0, da nur die halbe Fläche betrachtet wird und
folglich die Grenzen 0, da nur die halbe Fläche betrachtet wird und  .
.
Insgesamt ergibt sich damit für :
:
 Diese Gleichung gilt es nun nach
Diese Gleichung gilt es nun nach  zu lösen. Setze diese dazu mit
zu lösen. Setze diese dazu mit  gleich.
gleich.
Stellst du die Gleichung so um, dass auf einer Seite Null steht, so kannst du diese wie in den folgenden dargestellten Schritten mit deinem GTR lösen:![\(\begin{array}[t]{rll}
5&=&u \cdot f(u) - \displaystyle\int_{0}^{u} f(x)\;\mathrm dx \quad \scriptsize \mid\; -5\\[5pt]
0&=&u \cdot f(u) - \displaystyle\int_{0}^{u} f(x)\;\mathrm dx - 5
\end{array}\)](https://mathjax.schullv.de/11f6f0d1fd1594448d7ffd8a46b0f83101423a4c07b6c46843c53cda8316aa2b?color=5a5a5a) Übertrage nun den rechten Teil dieser Gleichung sowie den Funktionsterm von
Übertrage nun den rechten Teil dieser Gleichung sowie den Funktionsterm von  wie folgt in den Y= - Editor deines GTR:
wie folgt in den Y= - Editor deines GTR:
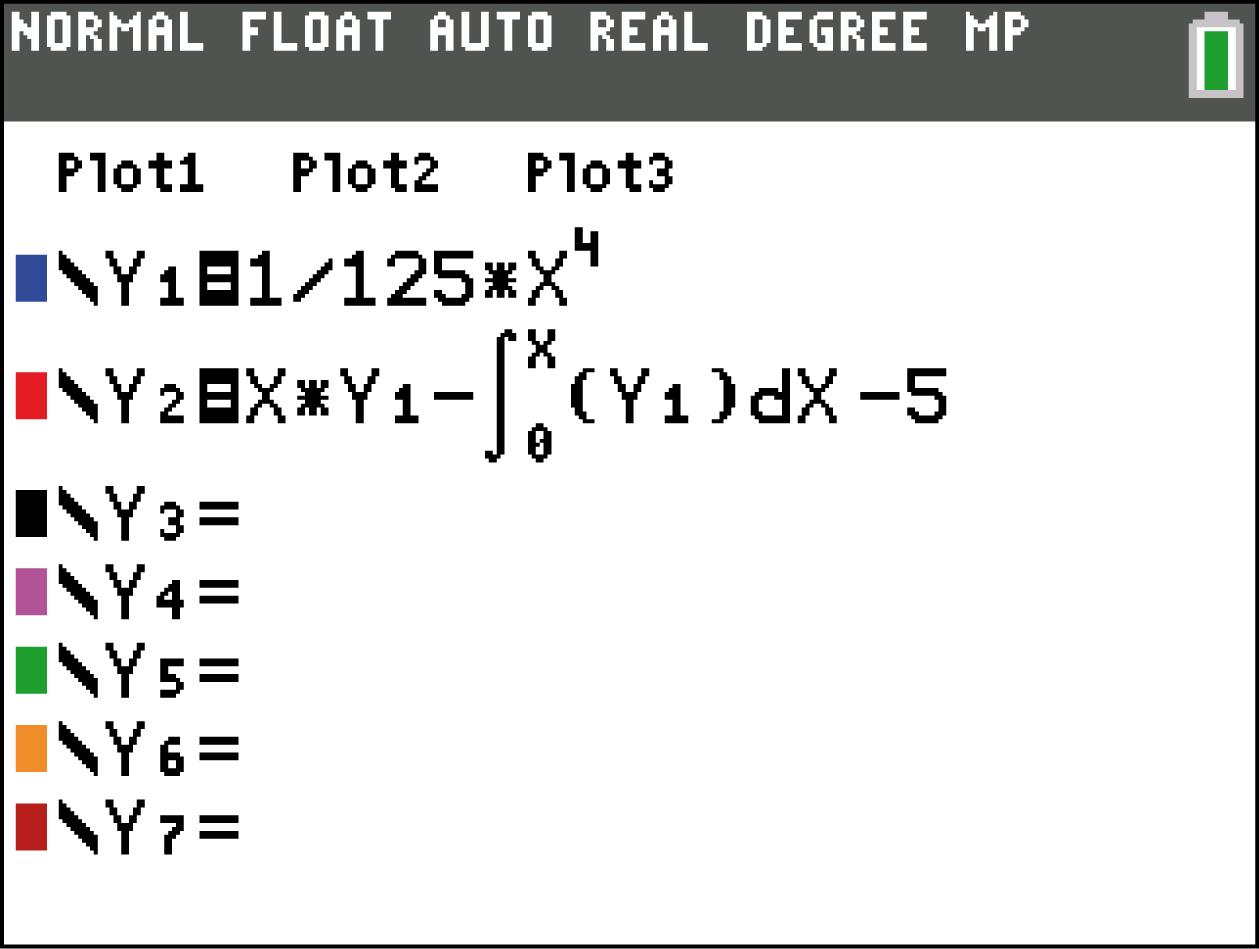 Wechsle nun in den Graph-Modus und berechne über die gegebene Eingabenfolge die Nullstelle der Gleichung und so den Wert für
Wechsle nun in den Graph-Modus und berechne über die gegebene Eingabenfolge die Nullstelle der Gleichung und so den Wert für  :
:
 ergibt sich also:
ergibt sich also: 
Die Breite der Zwischendecke beträgt folglich
der Zwischendecke beträgt folglich  .
.
Deine Aufgabe ist es nun, die Breite

Willst du die Breite
- Bestimme den Flächeninhalt
der Fläche, die die Zwischendecke mit
einschließt
- Stelle den Ansatz zur Berechnung des Flächeninhalts des halben Flächenstückes in Abhängigkeit von
auf
- Löse die Gleichung nach
und berechne die gesuchte Breite mit Hilfe deines GTR
Insgesamt ergibt sich damit für
Stellst du die Gleichung so um, dass auf einer Seite Null steht, so kannst du diese wie in den folgenden dargestellten Schritten mit deinem GTR lösen:

menu  CALC
CALC  2:Zero
2:Zero
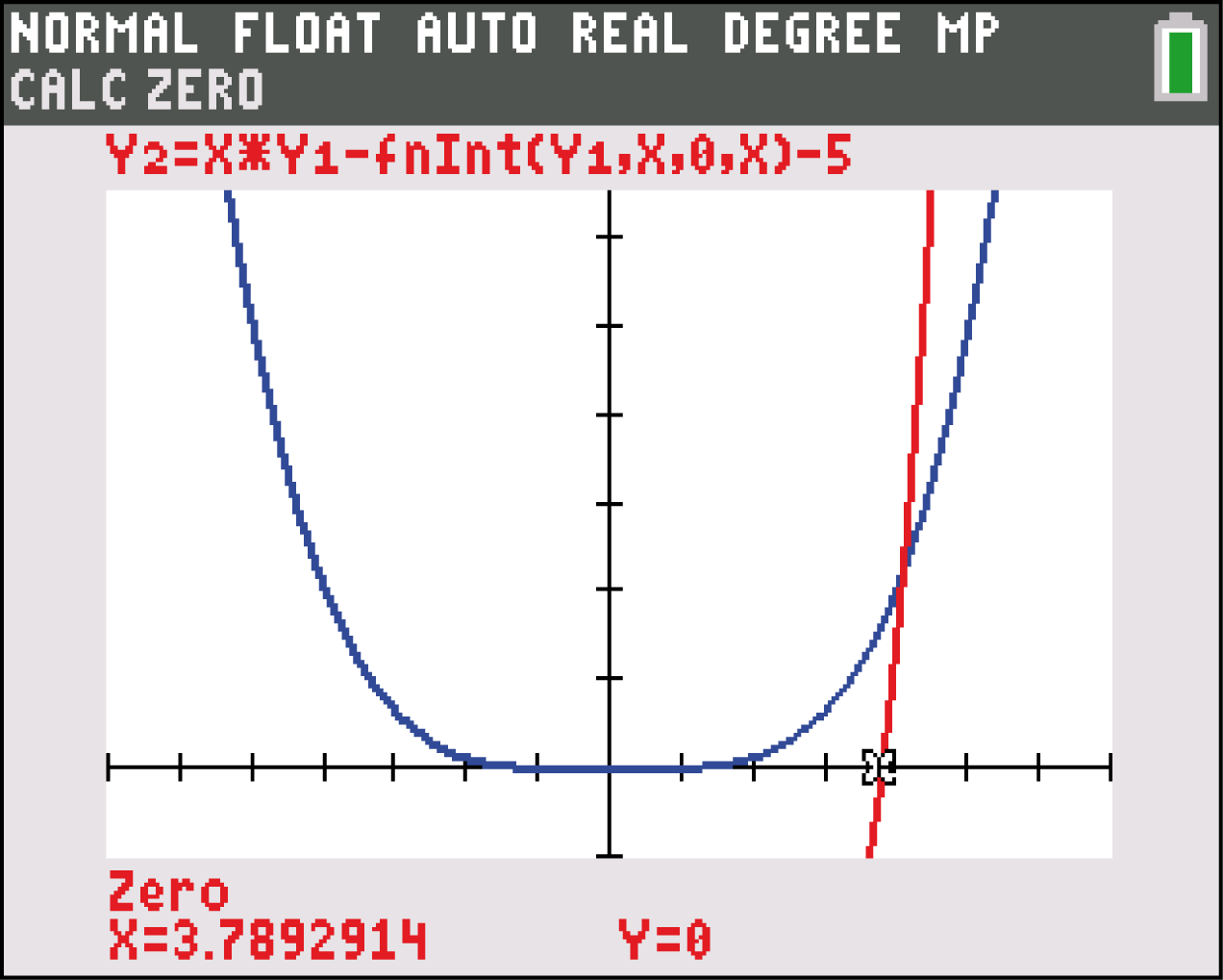
Für 
Die Breite
d)
Untersuchen, ob es möglich ist, dass Röhre die tiefste Stelle berührt
Nun sollst du untersuchen, ob sich eine zylinderförmige Röhre so in den Laderaum legen lässt, dass diese die tiefste Stelle des Laderaums bei  berührt.
berührt.
Würde sich die Röhre bis zum tiefsten Punkt des Laderaums absenken lassen, so würde der Abstand zwischen dem Mittelpunkt und jedem anderem Punkt auf dem Graphen von mindestens dem Radius
mindestens dem Radius  der Röhre entsprechen.
der Röhre entsprechen.
Formuliere also den Abstand zwischen dem Mittelpunkt der Röhre und jedem Punkt auf dem Graphen von
der Röhre und jedem Punkt auf dem Graphen von  als Funktion einer unbekannten Stelle
als Funktion einer unbekannten Stelle  . Verwende dazu die Koordinaten von
. Verwende dazu die Koordinaten von  für den Fall, dass sich die Röhre komplett absenken lassen würde.
für den Fall, dass sich die Röhre komplett absenken lassen würde.
Kann dann eine Stelle gefunden werden, dessen Abstand zum Mittelpunkt kleiner als der Radius der Röhre ist, so hast du gezeigt, dass die Röhre nicht den tiefsten Punkt berühren kann.
kleiner als der Radius der Röhre ist, so hast du gezeigt, dass die Röhre nicht den tiefsten Punkt berühren kann.
Berechne also das Minimum der Abstandsfunktion. Stelle die Funktion über den folgenden Ansatz für die Berechnung des Abstands zwischen zwei Punkten auf:
 und bestimme mit deinem GTR das Minimum dieser Funktion.
1. Schritt: Bestimmen der Abstandsfunktion
Der Mittelpunkt
und bestimme mit deinem GTR das Minimum dieser Funktion.
1. Schritt: Bestimmen der Abstandsfunktion
Der Mittelpunkt  der Röhre würde die Koordinaten
der Röhre würde die Koordinaten  besitzen, wenn diese sich vollständig absenken lassen würde. Jeder Punkt auf dem Graphen von
besitzen, wenn diese sich vollständig absenken lassen würde. Jeder Punkt auf dem Graphen von  kann über über
kann über über  beschrieben werden.
beschrieben werden.
Die Funktion lässt sich also wie folgt darstellen:
lässt sich also wie folgt darstellen:

 2. Schritt: Berechnen des Minimums
Übertrage nun wie den Funktionsterm von
2. Schritt: Berechnen des Minimums
Übertrage nun wie den Funktionsterm von  in den Y= Editor und greife ggf. über Vars auf den Funktionsterm von
in den Y= Editor und greife ggf. über Vars auf den Funktionsterm von  zu.
zu.
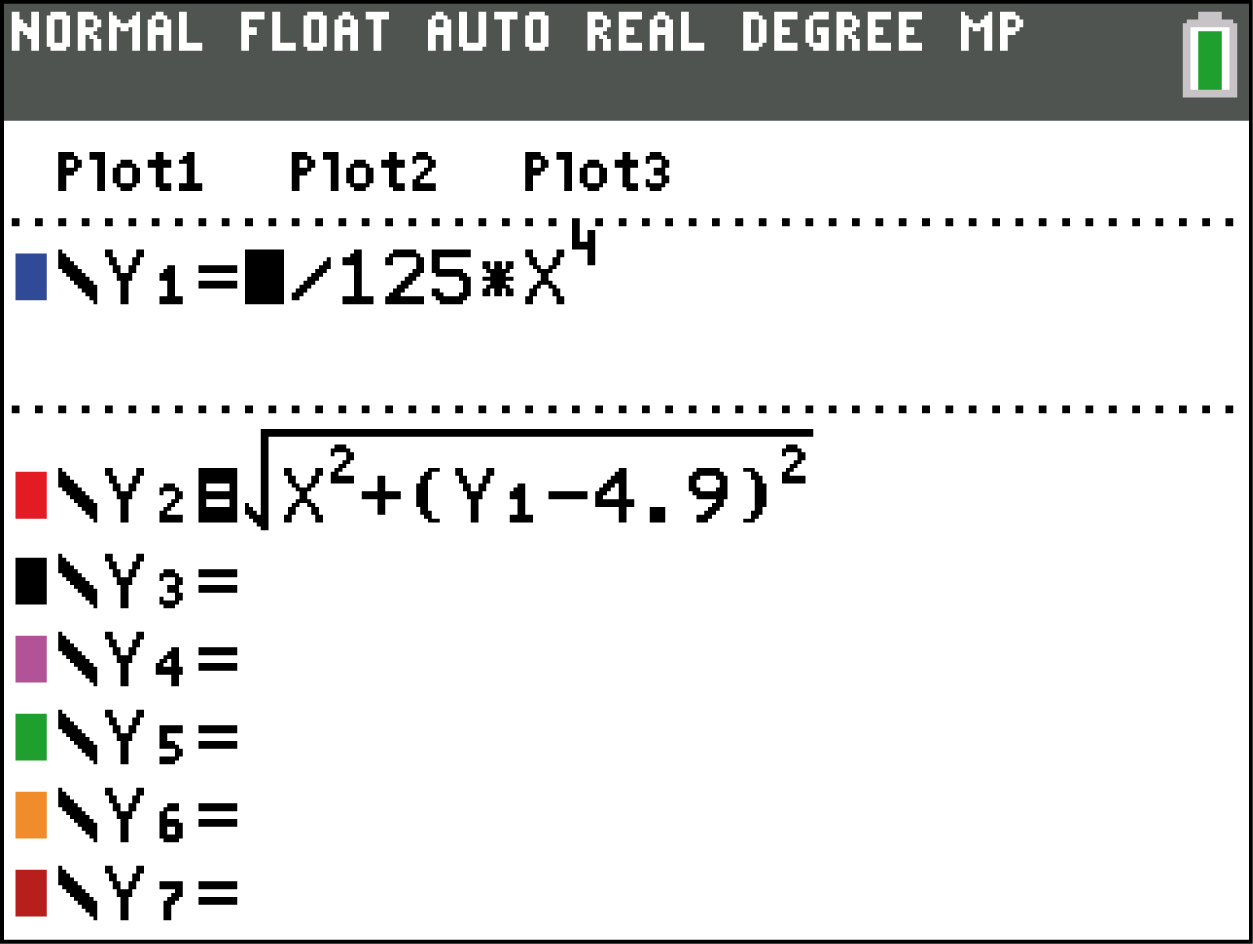 Wechsle nun in den Graphs-Modus und berechne das Minimum der Funktion:
Wechsle nun in den Graphs-Modus und berechne das Minimum der Funktion:
 m kleiner als der Radius mit 4,9
m kleiner als der Radius mit 4,9 m ist, berührt die Röhre nicht die tiefste Stelle bei
m ist, berührt die Röhre nicht die tiefste Stelle bei  im Laderaum.
im Laderaum.
Würde sich die Röhre bis zum tiefsten Punkt des Laderaums absenken lassen, so würde der Abstand zwischen dem Mittelpunkt und jedem anderem Punkt auf dem Graphen von
Formuliere also den Abstand zwischen dem Mittelpunkt
Kann dann eine Stelle gefunden werden, dessen Abstand zum Mittelpunkt
Berechne also das Minimum der Abstandsfunktion. Stelle die Funktion über den folgenden Ansatz für die Berechnung des Abstands zwischen zwei Punkten auf:
Die Funktion

2nd  CALC
CALC  3:minimum
3:minimum
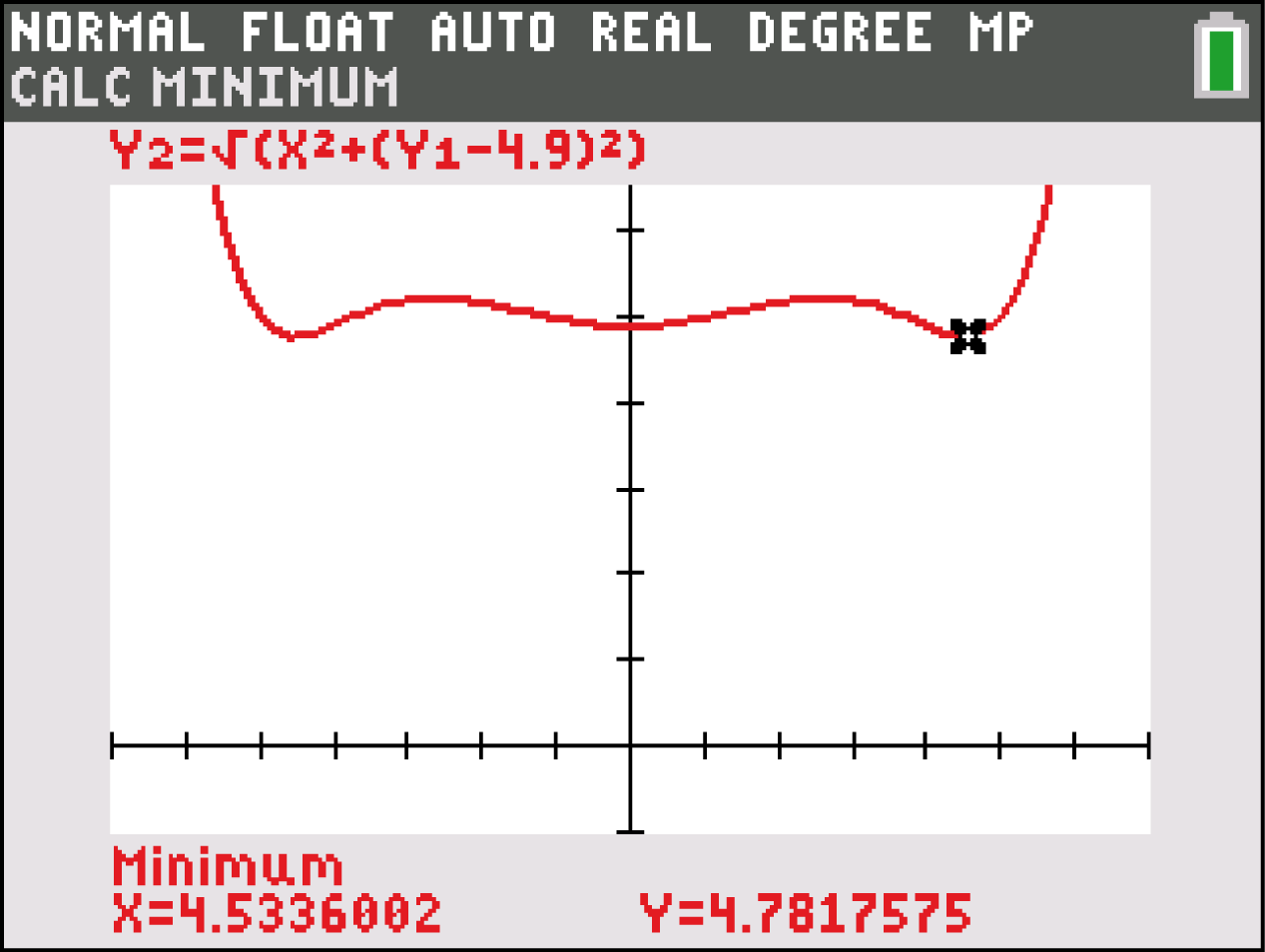
Da der minimale Abstand mit ungefähr 4,78
a)
Bestimmen der Tiefe des Laderaums in der Mitte
Der Aufgabenstellung kannst du hier entnehmen, dass der Querschnitt des Laderaums eines Lastkahns modellhaft durch die Funktion  beschrieben werden kann:
beschrieben werden kann:
 für
für  Willst du nun bestimmen, wie tief der Laderaum in der Mitte ist, so betrachte den Definitionsbereich der Funktion
Willst du nun bestimmen, wie tief der Laderaum in der Mitte ist, so betrachte den Definitionsbereich der Funktion  .
Da mit
.
Da mit  ein symmetrischer Definitionsbereich gegeben ist und da
ein symmetrischer Definitionsbereich gegeben ist und da  eine Funktion mit geraden Exponent ist, liegt die Mitte des Laderaums folglich an der Stelle
eine Funktion mit geraden Exponent ist, liegt die Mitte des Laderaums folglich an der Stelle  . Um die Tiefe zu bestimmen, musst du die Differenz zwischen den Funktionswerten von
. Um die Tiefe zu bestimmen, musst du die Differenz zwischen den Funktionswerten von  an den Stelle
an den Stelle  und
und  oder
oder  betrachten.
betrachten.
![\(\begin{array}[t]{rll}
f(x_M = 0)&=& \dfrac{1}{125} \cdot 0^4 = 0
\end{array}\)](https://mathjax.schullv.de/c10e893b984dd5f54384fb7b5aad7fe297a78836be90ab7d617b3a1bad183b5f?color=5a5a5a)
![\(\begin{array}[t]{rll}
f(x_M = 5)&=& \dfrac{1}{125} \cdot 5^4 = 5
\end{array}\)](https://mathjax.schullv.de/fba242ddea5fd8dff04b48011b99e2b1ec2b759ef08edb974c3aa9e04ddb85fc?color=5a5a5a) Die Differenz zwischen den Funktionswerten beträgt 5. Daraus folgt, dass der Laderaum in der Mitte eine Tiefe von 5 m besitzt.
Bestimmen der Breite des Laderaums in 3 m Höhe
Nun sollst du die Breite des Laderaums in 3 m Höhe bestimmen. Da
Die Differenz zwischen den Funktionswerten beträgt 5. Daraus folgt, dass der Laderaum in der Mitte eine Tiefe von 5 m besitzt.
Bestimmen der Breite des Laderaums in 3 m Höhe
Nun sollst du die Breite des Laderaums in 3 m Höhe bestimmen. Da  gilt, bedeutet das, dass du die
gilt, bedeutet das, dass du die  -Koordinaten zu
-Koordinaten zu  und
und  berechnen musst, um anhand dieser dann die Breite des Laderaums zu bestimmen.
berechnen musst, um anhand dieser dann die Breite des Laderaums zu bestimmen.
Da es sich bei um eine gerade Funktion handelt und da für diese
um eine gerade Funktion handelt und da für diese  gilt, ist es ausreichend den Funktionswert an einer dieser Stellen zu berechnen, um die Breite zu bestimmen.
gilt, ist es ausreichend den Funktionswert an einer dieser Stellen zu berechnen, um die Breite zu bestimmen.
![\(\begin{array}[t]{rll}
f(x_1) = 3&=& \dfrac{1}{125} \cdot x^4 \quad \scriptsize \mid\; \cdot 125\\[5pt]
-375&=&x^4 \quad \scriptsize \mid\; \sqrt[4]{\,}\\[5pt]
4,4&=&x
\end{array}\)](https://mathjax.schullv.de/c89074a1ca6001c40af5ac919efeea9747d2441ba15b9456a0a8c733f1d2d1fe?color=5a5a5a) Die Breite des Laderaums in 3 m Höhe beträgt also
Die Breite des Laderaums in 3 m Höhe beträgt also  Bestimmen des Bereichs mit einer Neigung unter 5 %
Hier ist der Bereich gesucht, in dem der Boden des Laderaums eine Neigung unter 5 % besitzt.
Bestimmen des Bereichs mit einer Neigung unter 5 %
Hier ist der Bereich gesucht, in dem der Boden des Laderaums eine Neigung unter 5 % besitzt.
Beachte hierbei, dass die Neigung des Laderaums durch die erste Ableitung der Funktion beschrieben werden kann. Diese gibt zu jeder Stelle
beschrieben werden kann. Diese gibt zu jeder Stelle  die Steigung der Funktion
die Steigung der Funktion  an und folglich bestimmt diese die Neigung des Rumpfes.
an und folglich bestimmt diese die Neigung des Rumpfes.
Willst du diese Aufgabe lösen, so bestimme zuerst die Stellen, an welchen die Neigung gleich 5 % ist. An diesen Stellen muss dann gelten:
 Bestimme dann mit diesen Stellen den gesuchten Bereich.
1. Schritt: Bestimmen der Ableitung von
Bestimme dann mit diesen Stellen den gesuchten Bereich.
1. Schritt: Bestimmen der Ableitung von  Die erste Ableitung von
Die erste Ableitung von  kannst du hier mittels Faktorregel bestimmen.
kannst du hier mittels Faktorregel bestimmen.
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{125} \cdot x^4 \\[5pt]
f‘(x)&=& \dfrac{4}{125} \cdot x^3
\end{array}\)](https://mathjax.schullv.de/f28f59f6db174658dd761e29806d07f25bcda75222c282b311650e40f0d5ad69?color=5a5a5a) 2. Schritt: Bestimmen der Stellen mit einer Neigung von 5 %
Setze nun den Funktionsterm von
2. Schritt: Bestimmen der Stellen mit einer Neigung von 5 %
Setze nun den Funktionsterm von  mit 0,05 gleich, um die Stellen mit einem Anstieg von 5 % zu bestimmen:
mit 0,05 gleich, um die Stellen mit einem Anstieg von 5 % zu bestimmen:
![\(\begin{array}[t]{rll}
f‘(x)&=& 0,05 \\[5pt]
0,05&=& \dfrac{4}{125} \cdot x^3 \quad \scriptsize \mid\; \cdot \dfrac{125}{4}\\[5pt]
1,5625&=& x^3 \quad \scriptsize \mid\; \sqrt[3]{\;}\\[5pt]
1,16&=& x
\end{array}\)](https://mathjax.schullv.de/c03cff72c20f07b72a78207c175b208a3b8f0d0ab952c92656d59e5788a036ee?color=5a5a5a) Aufgrund der Symmetrie und der oben beschrieben Eigenschaften des Graphen von
Aufgrund der Symmetrie und der oben beschrieben Eigenschaften des Graphen von  ergibt sich hier, dass der Laderaum bis zu 1,16 m links und 1,16 m rechts von der Mitte eine Neigung besitzt, die kleiner als 5 % ist.
Berechnen des Volumens des Laderaums
Der Querschnitt des Laderaums ist auf der gesamten Länge gleich und wird durch den Graphen der Funktion
ergibt sich hier, dass der Laderaum bis zu 1,16 m links und 1,16 m rechts von der Mitte eine Neigung besitzt, die kleiner als 5 % ist.
Berechnen des Volumens des Laderaums
Der Querschnitt des Laderaums ist auf der gesamten Länge gleich und wird durch den Graphen der Funktion  beschrieben. Weiterhin kannst du der Aufgabenstellung entnehmen, dass der Laderaum des Lastkahns eine Länge von 50 m besitzt.
beschrieben. Weiterhin kannst du der Aufgabenstellung entnehmen, dass der Laderaum des Lastkahns eine Länge von 50 m besitzt.
Deine Aufgabe ist es nun das Volumen des Laderaums zu berechnen. Beim Laderaum handelt es sich also um einen Körper. Dieser Körper besitzt eine Grundfläche , in Form des Querschnitts des Laderaums und eine Länge von
, in Form des Querschnitts des Laderaums und eine Länge von  . Das Volumen berechnet sich dann über folgende Formel:
. Das Volumen berechnet sich dann über folgende Formel:
 Gehe wie folgt vor, um das Volumen
Gehe wie folgt vor, um das Volumen  des Laderaums zu berechnen:
des Laderaums zu berechnen:
 Der Querschnitt des Laderaums wird über den Graphen von
Der Querschnitt des Laderaums wird über den Graphen von  im Bereich
im Bereich  beschrieben. Betrachte vor dem Integrieren den Graphen der Funktion
beschrieben. Betrachte vor dem Integrieren den Graphen der Funktion  im GRAPH Modus deines GTR:
im GRAPH Modus deines GTR:
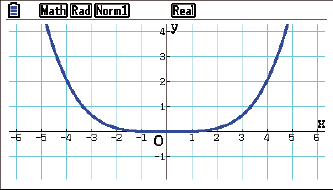 Oben kannst du sehen, dass sich der Graph von
Oben kannst du sehen, dass sich der Graph von  im betrachteten Bereich oberhalb der
im betrachteten Bereich oberhalb der  -Achse befindet. Möchtest du nun die Querschnittsfläche berechnen, so berechne zunächst die Fläche eines Rechtecks mit der Höhe und der Breite des Querschnitts und subtrahiere von dieser dann das Integral über
-Achse befindet. Möchtest du nun die Querschnittsfläche berechnen, so berechne zunächst die Fläche eines Rechtecks mit der Höhe und der Breite des Querschnitts und subtrahiere von dieser dann das Integral über  im Bereich
im Bereich  und
und  .
.
Das Integral über im betrachteten Bereich kannst du ebenfalls im GRAPH deines GTR berechnen:
SHIFT
im betrachteten Bereich kannst du ebenfalls im GRAPH deines GTR berechnen:
SHIFT  G-Slov
G-Slov 
 dx
Mit dem GTR folgt:
dx
Mit dem GTR folgt:
 Willst du nun den Flächeninhalt
Willst du nun den Flächeninhalt  der Querschnittsfläche berechnen, so subtrahiere vom Flächeninhalt des oben beschriebenen Rechtecks die berechneten 10
der Querschnittsfläche berechnen, so subtrahiere vom Flächeninhalt des oben beschriebenen Rechtecks die berechneten 10  ;
2. Schritt: Berechnen des Volumens
;
2. Schritt: Berechnen des Volumens  Setze
Setze  und
und  in die Volumenformel ein, um das gesuchte
in die Volumenformel ein, um das gesuchte  zu berechnen:
zu berechnen:
![\(\begin{array}[t]{rll}
V&=&40\,\text{m}^2 \cdot 50\,\text{m} = 2.000\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/8afb2c333992a6164a517dbd239a728267d07e622c62a5b793e45a290a46519d?color=5a5a5a) Der Laderaum besitzt ein Volumen von
Der Laderaum besitzt ein Volumen von  .
.
Da es sich bei
Beachte hierbei, dass die Neigung des Laderaums durch die erste Ableitung der Funktion
Willst du diese Aufgabe lösen, so bestimme zuerst die Stellen, an welchen die Neigung gleich 5 % ist. An diesen Stellen muss dann gelten:
Deine Aufgabe ist es nun das Volumen des Laderaums zu berechnen. Beim Laderaum handelt es sich also um einen Körper. Dieser Körper besitzt eine Grundfläche
- Berechne den Flächeninhalt des Querschnitts. Verwende hierzu ein Integral und deinen GTR
- Setze
und
in die Volumenformel ein und berechne das Volumen

Das Integral über

b)
Berechnen des Abstands der Stützen zueinander
Der Lastkahn steht zur Wartung auf einer ebenen Plattform an Land. Dort wird er durch gerade Stützen stabilisiert, die orthogonal zur Außenwand angebracht sind. Die Befestigungspunkte dieser Stützen sind:
Willst du den Abstand berechnen, so musst du zunächst die Stützen durch Geraden beschreiben und über den Schnittpunkt dieser mit der -Achse den gesuchten Abstand berechnen.
-Achse den gesuchten Abstand berechnen.
Gehe dabei so vor: zur Stütze zu
zur Stütze zu  Dir ist bekannt, dass die Stütze am Punkt
Dir ist bekannt, dass die Stütze am Punkt  orthogonal zur Außenwand verläuft. Daraus folgt, dass die gesuchte Gerade
orthogonal zur Außenwand verläuft. Daraus folgt, dass die gesuchte Gerade  der Normalen an den Graphen von
der Normalen an den Graphen von  im Punkt
im Punkt  entspricht.
entspricht.
Die Steigung von
von  kannst du mit diesem Zusammenhang
kannst du mit diesem Zusammenhang
 und der Ableitung
und der Ableitung  von
von  berechnen:
Den
berechnen:
Den  -Achsenabschnitt der Geraden
-Achsenabschnitt der Geraden  berechnest du über eine Punktprobe mit dem Punkt
berechnest du über eine Punktprobe mit dem Punkt  :
Gerade
:
Gerade  ergibt sich also zu:
ergibt sich also zu:  2. Schritt: Bestimmen des Schnittpunkts der Geraden
2. Schritt: Bestimmen des Schnittpunkts der Geraden  mit der
mit der  -Achse
Den Schnittpunkt von
-Achse
Den Schnittpunkt von  mit der
mit der  -Achse bestimmst du, indem du den Funktionsterm von
-Achse bestimmst du, indem du den Funktionsterm von  mit gleich Null setzt und die Gleichung nach
mit gleich Null setzt und die Gleichung nach  auflöst:
auflöst:
 schneidet also bei
schneidet also bei  die
die  -Achse. Beachte wieder die Symmetrie des Graphen von
-Achse. Beachte wieder die Symmetrie des Graphen von  um den Abstand
um den Abstand  zwischen den Stützen zu berechnen:
zwischen den Stützen zu berechnen:
![\(\begin{array}[t]{rll}
d&=& 2 \cdot \left|-8,16\right| = 16,32 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b3ab868dd1fbde94880ee1c72545c6af5cd94a338b59334ca0f4081e2853a289?color=5a5a5a) Der Abstand zwischen den zwei Stützen ist 16,32 m
Der Abstand zwischen den zwei Stützen ist 16,32 m
Willst du den Abstand berechnen, so musst du zunächst die Stützen durch Geraden beschreiben und über den Schnittpunkt dieser mit der
Gehe dabei so vor:
- Bestimme die Steigung der Geraden der Stütze zu
über die Steigung der zugehörigen Normalen
- Ermittle den
-Achsenabschnitt über eine Punktprobe
- Bestimme die Schnittstelle mit der
-Achse und bestimme mittels der Symmetrie des Graphen von
den gesuchten Abstand
Die Steigung
c)
Berechnen der Breite der Zwischendecke
Der Laderaum kann durch eine horizontale Zwischendecke der Länge 50 m in zwei Teilräume geteilt werden. Das Volumen des unteren Teilraums beträgt dann 500  .
.
Deine Aufgabe ist es nun, die Breite der Zwischendecke zu berechnen. Fertige dir dazu zunächst eine Skizze an:
der Zwischendecke zu berechnen. Fertige dir dazu zunächst eine Skizze an:
 Willst du diese Aufgabe lösen, so musst du hier mit einem Integral arbeiten. Dabei ist es vorteilhaft nur einen Teil der gesamten Fläche zu betrachten, denn diese lässt sich in zwei gleich große Flächenstücke zerteilen.
Willst du diese Aufgabe lösen, so musst du hier mit einem Integral arbeiten. Dabei ist es vorteilhaft nur einen Teil der gesamten Fläche zu betrachten, denn diese lässt sich in zwei gleich große Flächenstücke zerteilen.
Willst du die Breite der Zwischendecke berechnen, so dir bekannt sein, an welcher Stelle
der Zwischendecke berechnen, so dir bekannt sein, an welcher Stelle  diese am Graphen der Funktion
diese am Graphen der Funktion  anliegt. Gehe dazu so vor:
anliegt. Gehe dazu so vor:
 Willst du berechnen, welchen Flächeninhalt
Willst du berechnen, welchen Flächeninhalt  die Zwischendecke mit dem Graphen von
die Zwischendecke mit dem Graphen von  einschließt, so setze
einschließt, so setze  und
und  in die Volumenformel aus der Teilaufgabe a ein:
in die Volumenformel aus der Teilaufgabe a ein:
![\(\begin{array}[t]{rll}
V&=&A \cdot l \quad \scriptsize \mid\;: l \\[5pt]
A&=&\dfrac{500\,\text{m}^3}{50\,\text{m}} = 10\,\text{m}^2\\[5pt]
\end{array}\)](https://mathjax.schullv.de/7ab1b70385951c78c76ab4d71d80d3d30d728f684c5357fa4256354ede1a4c85?color=5a5a5a) Der Flächeninhalt des betrachteten halben Flächenstücks ist also:
Der Flächeninhalt des betrachteten halben Flächenstücks ist also:  2. Schritt: Bestimmen der gesuchten Breite
Analog zum Aufgabenteil a berechnet sich der Flächeninhalt der halben Fläche über eine Rechteckfläche und ein Integral über den Graphen von
2. Schritt: Bestimmen der gesuchten Breite
Analog zum Aufgabenteil a berechnet sich der Flächeninhalt der halben Fläche über eine Rechteckfläche und ein Integral über den Graphen von  . Das hier betrachtete Rechteck besitzt dabei die Länge
. Das hier betrachtete Rechteck besitzt dabei die Länge  und die Höhe
und die Höhe  . Das Integral über
. Das Integral über  folglich die Grenzen 0, da nur die halbe Fläche betrachtet wird und
folglich die Grenzen 0, da nur die halbe Fläche betrachtet wird und  .
.
Insgesamt ergibt sich damit für :
:
 Diese Gleichung gilt es nun nach
Diese Gleichung gilt es nun nach  zu lösen. Setze diese dazu mit
zu lösen. Setze diese dazu mit  gleich.
gleich.
Stellst du die Gleichung so um, dass auf einer Seite Null steht, so kannst du diese wie in den folgenden dargestellten Schritten mit deinem GTR lösen:![\(\begin{array}[t]{rll}
5&=&u \cdot f(u) - \displaystyle\int_{0}^{u} f(x)\;\mathrm dx \quad \scriptsize \mid\; -5\\[5pt]
0&=&u \cdot f(u) - \displaystyle\int_{0}^{u} f(x)\;\mathrm dx - 5
\end{array}\)](https://mathjax.schullv.de/11f6f0d1fd1594448d7ffd8a46b0f83101423a4c07b6c46843c53cda8316aa2b?color=5a5a5a) Übertrage nun den rechten Teil dieser Gleichung sowie den Funktionsterm von
Übertrage nun den rechten Teil dieser Gleichung sowie den Funktionsterm von  wie folgt in den Graph - Modus deines GTR:
wie folgt in den Graph - Modus deines GTR:
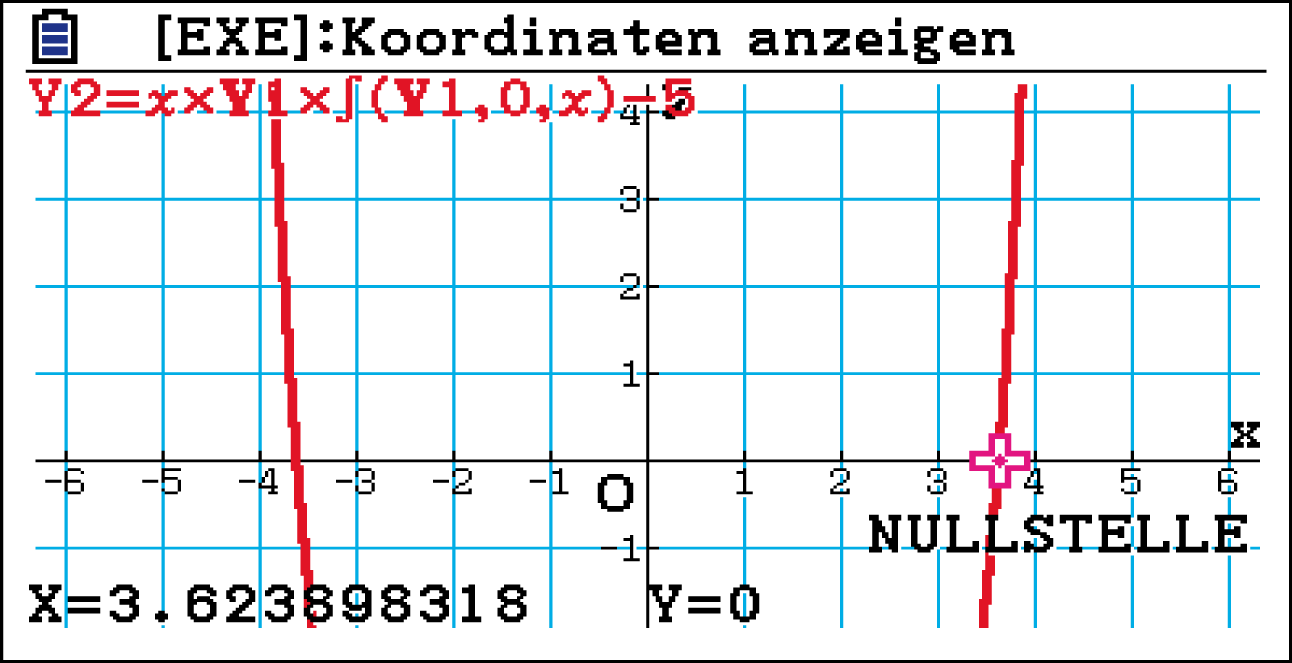
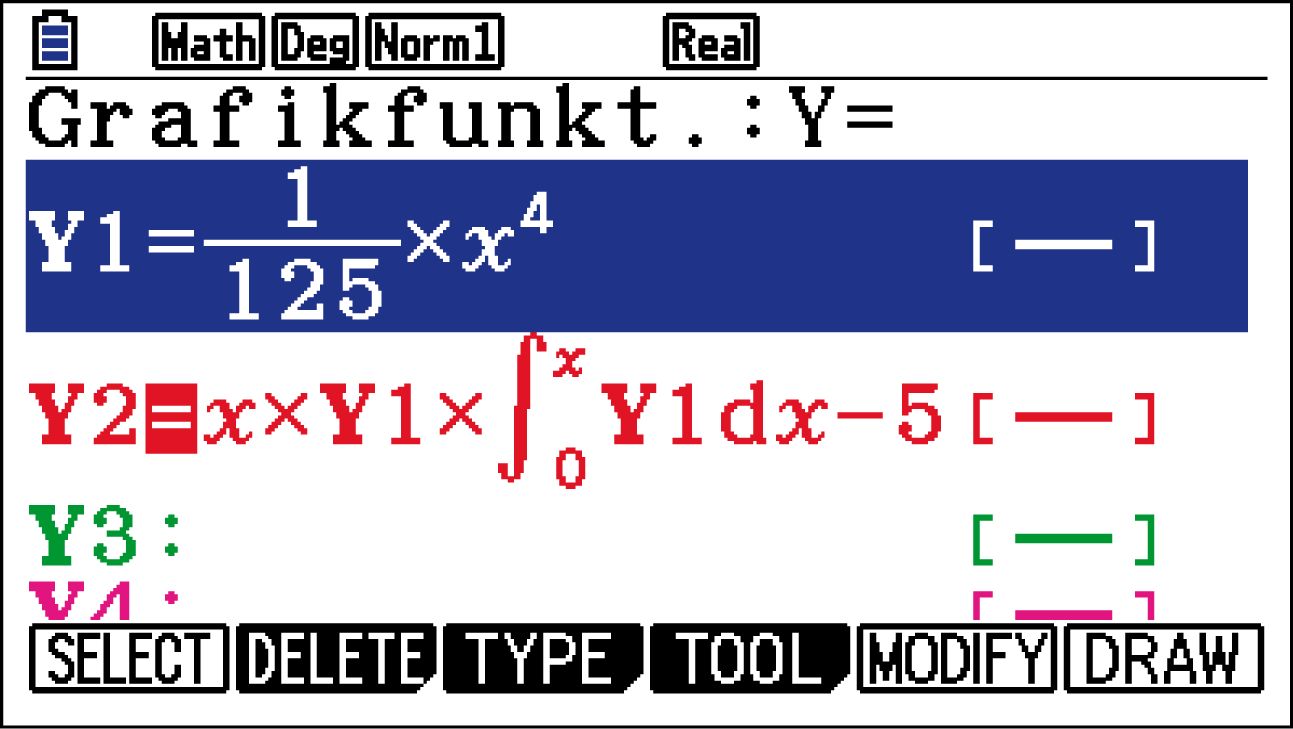 Wechsle nun in den Graph-Modus und berechne über die gegebene Eingabenfolge die Nullstelle der Gleichung und so den Wert für
Wechsle nun in den Graph-Modus und berechne über die gegebene Eingabenfolge die Nullstelle der Gleichung und so den Wert für  :
:
 ergibt sich also:
ergibt sich also: 
Die Breite der Zwischendecke beträgt folglich
der Zwischendecke beträgt folglich  .
.
Deine Aufgabe ist es nun, die Breite

Willst du die Breite
- Bestimme den Flächeninhalt
der Fläche, die die Zwischendecke mit
einschließt
- Stelle den Ansatz zur Berechnung des Flächeninhalts des halben Flächenstückes in Abhängigkeit von
auf
- Löse die Gleichung nach
und berechne die gesuchte Breite mit Hilfe deines GTR
Insgesamt ergibt sich damit für
Stellst du die Gleichung so um, dass auf einer Seite Null steht, so kannst du diese wie in den folgenden dargestellten Schritten mit deinem GTR lösen:

OPTN  CALC
CALC 
 dx
dx
Für 
Die Breite
d)
Würde sich die Röhre bis zum tiefsten Punkt des Laderaums absenken lassen, so würde der Abstand zwischen dem Mittelpunkt und jedem anderem Punkt auf dem Graphen von
Formuliere also den Abstand zwischen dem Mittelpunkt
Kann dann eine Stelle gefunden werden, dessen Abstand zum Mittelpunkt
Berechne also das Minimum der Abstandsfunktion. Stelle die Funktion über den folgenden Ansatz für die Berechnung des Abstands zwischen zwei Punkten auf:
Die Funktion

SHIFT  G-Slov
G-Slov  MIN
MIN
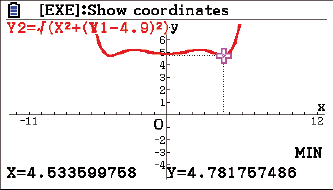
Da der minimale Abstand mit ungefähr 4,78