Bei einem dieser Gewächshäuser können die Ecken der Dachfläche durch die Punkte , , und beschrieben werden.
Stelle dieses Gewächshaus in einem geeigneten Koordinatensystem dar. Berechne den Rauminhalt dieses Gewächshauses. Ermittle eine Koordinatengleichung der Ebene, die die Lage der Dachfläche beschreibt.

Die Firma bietet die Gewächshäuser mit unterschiedlichen Neigungen der Dachflächen an. Die Lage jeder dieser Dachflächen kann durch eine Ebene beschrieben werden, die zur Schar mit gehört.
Berechne den Wert von a, für den die Neigung der Dachfläche beträgt. Es gibt eine Gerade g, die in allen Ebenen der Ebenenschar liegt.
Bestimme eine Gleichung dieser Geraden g. Untersuche, für welche Werte von im gesamten Gewächshaus eine Mindesthöhe von gegeben ist.

Rauminhalt
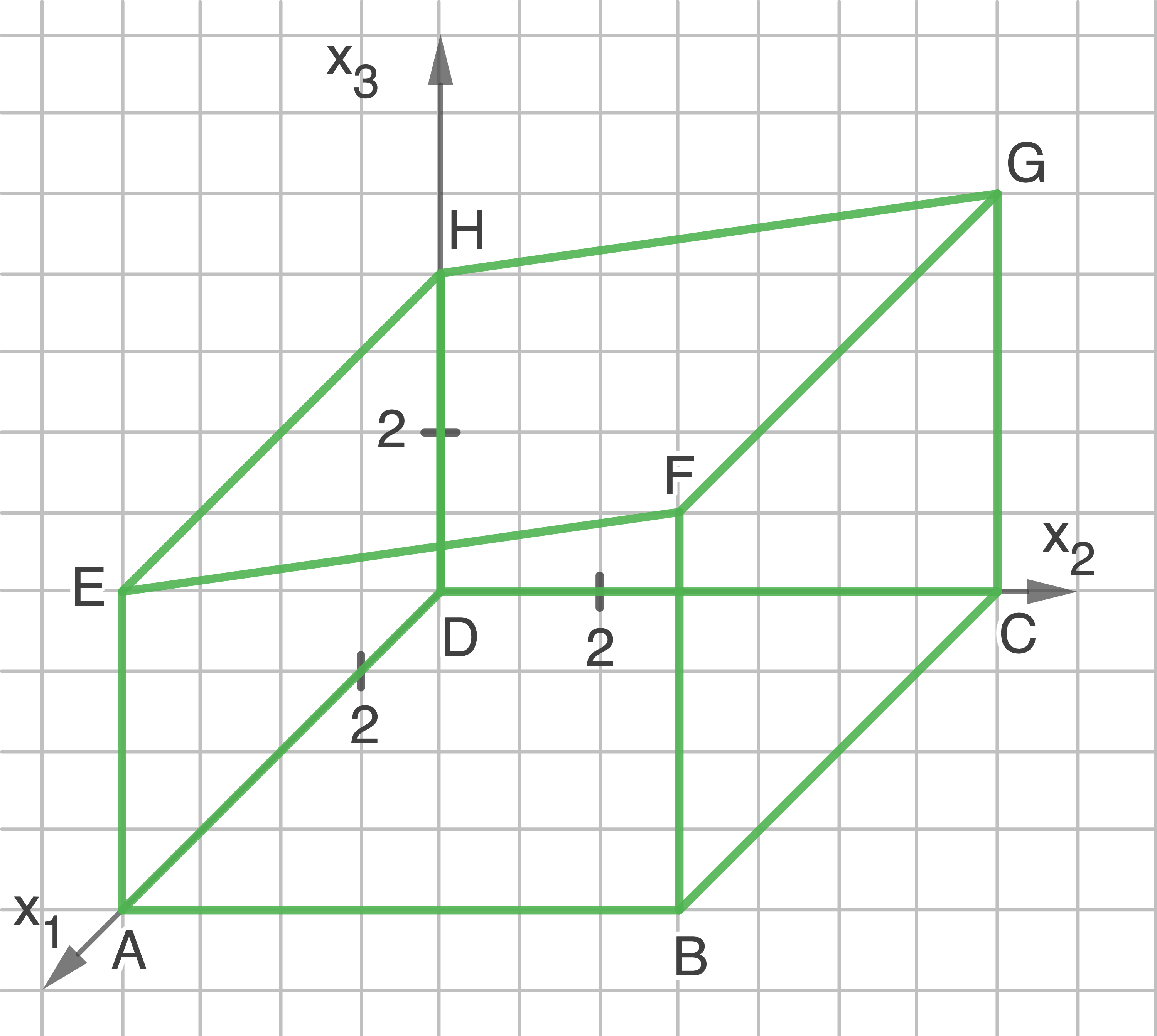
Bei dem Gewächshaus handelt es sich um ein Prisma mit der trapezförmigen Grundfläche Für das Volumen folgt: Der Rauminhalt des Gewächshauses beträgt Koordinatengleichung
Durch die folgenden beiden Vektoren kann die Ebene aufgespannt werden: Mit dem Kreuzprodukt folgt ein möglicher Normalenvektor: Eine Koordinatengleichung der Ebene, die die Lage der Dachfläche beschreibt, lautet

Wert von a
Ein Normalenvektor der Ebene ist , ein Normalenvektor der Ebene ist Mit der Formel für den Schnittwinkel zweier Ebenen folgt: Wegen ergibt sich als Lösung Geradengleichung
Die gesuchte Gerade ist die Schnittgerade der Ebenen, folglich wird die Schnittgerade von und berechnet: Aus dem LGS ergeben sich und mit Daraus ergibt sich folgende Geradengleichung: Mindesthöhe
Das Rechteck stellt die hohe Wand dar. Die Punkte und liegen auf und deshalb ist diese Höhe für alle Werte von konstant. Der Punkt liegt auf der Ebene und die Koordinate stellt die Höhe der Wand dar. Es muss folglich gelten und somit folgt