Wahlteil A1

Aufgabe A 1.1

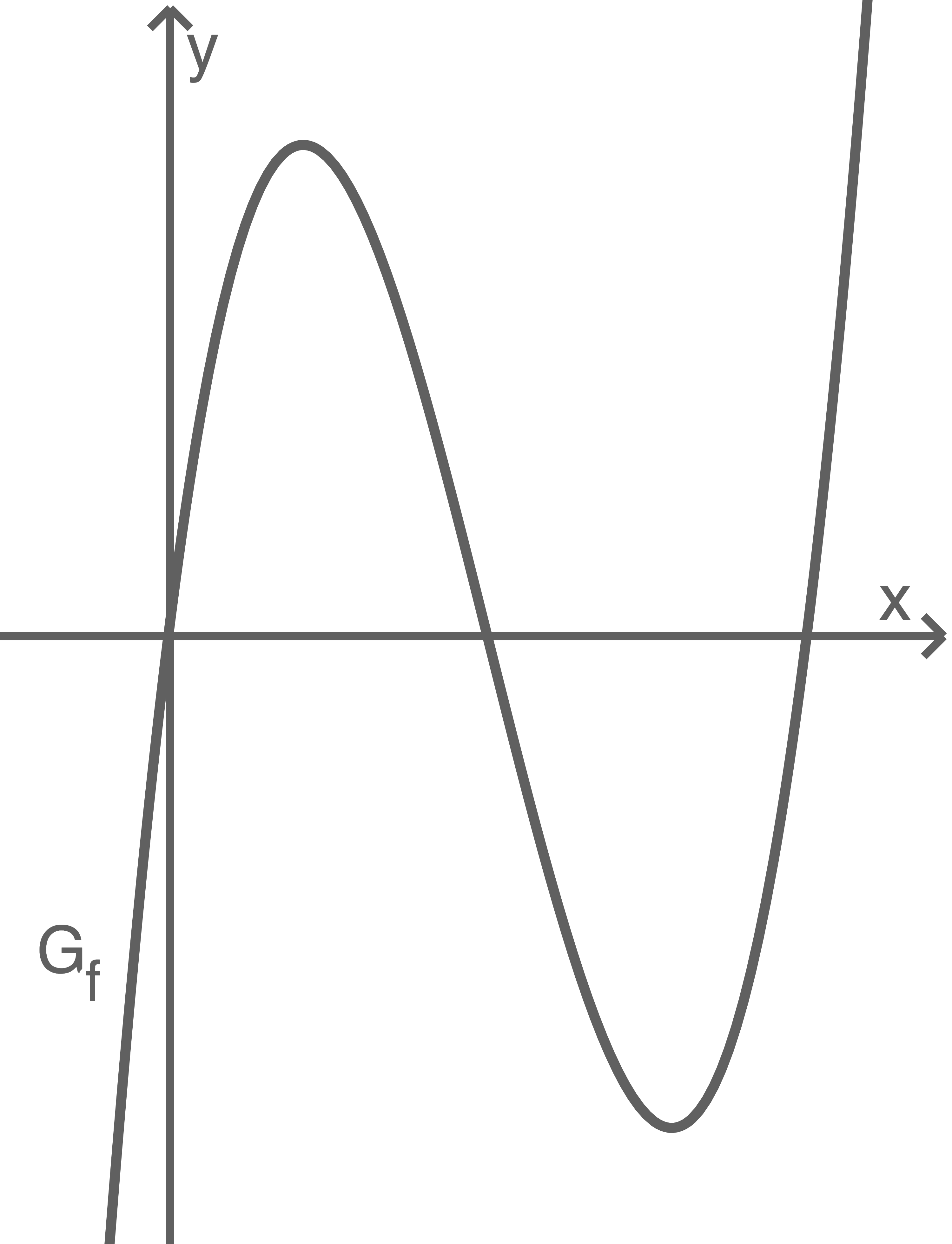
Die Abbildung zeigt den Graphen $G_f$ der Funktion $f$ mit $f(x)=x^3-6x^2+8x$ .

Berechne die Nullstelle von $f$ .

(1,5 VP)

Berechne die Koordinaten des Wendepunktes $W$ von $G_f$ .

(1,5 VP)

Die Gerade $t_1$ ist die Tangente an $G_f$ in $W$ .
Zeige, dass $y=-4x+8$ eine Gleichung von $t_1$ ist.

(1 VP)

Die Gerade $t_2$ ist die Tangente an $G_f$ im Ursprung $O$ . Die Geraden $t_1$ und $t_2$ schneiden sich im Punkt $Q$ . Berechne für das Dreieck $OWQ$ die Weite des Innenwinkels bei $Q$ .

(2 VP)

Für ein $u>0$ ist die Tangente an $G_f$ im Punkt $B(u\mid f(u))$ parallel zu $t_2$ . Bestimme den Wert von $u$ .

(1,5 VP)

Die Funktion $I_0$ mit $I_0(x)=\displaystyle\int_{0}^{x}f(t)\;\mathrm dt$ besitzt im Intervall $[0;4]$ ihren maximalen Wert an der Stelle $x_0$ . Gib $x_0$ an und begründe deine Angabe.

(1,5 VP)

Für die Funktion $h$ mit $h(x)=x^3-4x$ gilt $f(x)=h(x-2)$ . Erläutere, welche Symmetrieeigenschaft daraus für $G_f$ folgt.

(1,5 VP)

Der Graph $G_{f*}$ entsteht durch Spiegelung des Graphen $G_f$ an der Geraden mit der Gleichung $x=a.$
Die Tangente an $G_{f*}$ im Wendepunkt von $G_{f*}$ schneidet die $y$ -Achse im Punkt $S(0 \mid 16).$
Bestimme den Wert von $a.$

(2,5 VP)

Aufgabe A 1.2

Für jedes $a \gt 0$ ist die Funktion $f_a$ gegeben durch $f_a(x)=a\cdot \sin(a\cdot \pi \cdot x)$ . Die zugehörigen Graphen werden mit $G_a$ bezeichnet. Der Punkt $H_a\pmatrix{\dfrac{1}{2a}\mid a}$ ist ein Hochpunkt von $G_a.$

Gib die Periode von $f_a$ an.

(0,5 VP)

Der Punkt $H_a$ bildet mit den beiden von $H_a$ am wenigsten weit entfernten Tiefpunkten von $G_a$ ein Dreieck. Zeige, dass der Flächeninhalt dieses Dreiecks unabhängig von $a$ ist.

(2 VP)

Ermittle den Wert von $a$ , für den $H_a$ vom Ursprung den Abstand $1$ hat.

(2 VP)

Bestimme eine Gleichung der Kurve $K$ , auf der alle Punkte $H_a$ liegen.

(1 VP)

Auf $K$ gibt es einen Punkt $H_a$ , in dem die Tangente an $K$ parallel zur Geraden mit der Gleichung $y=-2x$ ist.
Bestimme den Wert von $a.$

(1,5 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung A 1.1

Nullstellen bestimmen:

$\begin{array}[t]{rll} f(x)&=&0& \\[5pt] x^3-6x^2+8x&=& 0 \\[5pt] x\cdot(x^2-6x+8)&=& 0 \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt $x_1=0$ und $x^2-6x+8=0.$

Anwenden der $pq-$ Formel:

$\begin{array}[t]{rll} x_{2;3}&=&-\dfrac{(-6)}{2}\pm\sqrt{\left(\dfrac{-6}{2}\right)^2 -8} & \\[5pt] x_{2;3}&=& 3\pm\sqrt{9 -8}& \\[5pt] x_{2;3}&=&3\pm\sqrt{1} & \\[5pt] \end{array}$

Es folgt: $x_2=2$ und $x_3=4.$

Koordinaten des Wendepunkts berechnen:

Erste und zweite Ableitung bilden:

$\(f$

Notwendige Bedingung für Wendestellen anwenden:

$\(\begin{array}[t]{rll} f$

Hinreichende Bedingung für Wendestellen prüfen:

$\(f$

Bestimmung der $y$ -Koordinate:

$\begin{array}[t]{rll} f(2)&=&2^3-6\cdot2^2+8\cdot2 & \\[5pt] f(2)&=&0 & \\[5pt] \end{array}$

Die Koordinaten des Wendepunkts folgen mit $W(2\mid0).$

Tangentengleichung überprüfen:

$y=-4x+8$

Punktprobe mit $W(2\mid0)$ :

$\begin{array}[t]{rll} 0&=&-4\cdot2+8 & \\[5pt] 0&=&0 \end{array}$

Steigung an der Stelle $x=2$ überprüfen:

$\(\begin{array}[t]{rll} f$

Da der Punkt $W$ in $y$ liegt und die Steigung an der Stellle $x=2$ der Tangentensteigung von $y$ entspricht, ist $y=-4x+8$ eine Gleichung von $t_1.$

Innenwinkel bei $Q$ berechnen:

Die Winkelsumme eines Dreiecks beträgt $180^{\circ}.$

Innenwinkel bei $O:$

$\(\begin{array}[t]{rll} \tan(\alpha_1)&=& f$

Innenwinkel bei $W:$

$\(\begin{array}[t]{rll} \tan(\alpha_2)&=&\mid f$

Innenwinkel bei $Q:$

$\begin{array}[t]{rll} 180°&=\, \alpha_1+\alpha_2+\alpha_3 & \\[5pt] 180°&= \, 82,9°+76,0°+\alpha_3 & \\[5pt] 180°&=\, 158,9°+\alpha_3 &\quad \scriptsize \mid\;-158,9° \\[5pt] 21,1°&=\, \alpha_3 \end{array}$

Wert von $u$ bestimmen:

Voraussetzung für die Parallelität ist, dass $t_u$ die gleiche Steigung wie $t_2$ hat. Somit lässt sich $u$ wie folgt berechnen:

$\(\begin{array}[t]{rll} f$

Durch Anwendung des Satzes vom Nullprodukt ergeben sich die Lösungen $u_1=0$ und $u_2=4.$ Wegen der Voraussetzung $u>0$ folgt $u=4$ als einzige Lösung.

Die Funktion $I_0$ beschreibt den orientierten Flächeninhalt zwischen dem Graphen von $f$ und der $x$ - Achse. Der Graph von $f$ verläuft für $0\lt x\lt2$ oberhalb und für $2\lt x\lt4$ unterhalb der $x-$ Achse. Daher ist $x_0=2.$

Der Graph $G_h$ von $h$ ist punktsymmetrisch zum Ursprung, denn der Funktionsterm von $h$ enthält nur Potenzen mit ungeraden Exponenten. $G_f$ ist gegenüber $G_h$ um 2 Einheiten nach rechts verschoben, also ist $G_f$ punktsymmetrisch zu $W(2\mid 0).$

Da die Tangente am Wendepunkt von $G_{f*}$ symmetrisch zu der Tangente am Wendepunkt von $G_f$ ist, muss die Steigung 4 betragen. Durch Einsetzen des enthaltenen Punkt $S$ folgt nun die Tangentengleichung:

$\begin{array}[t]{rll} 16&=& 4\cdot0+c & \\[5pt] 16&=& c \end{array}$

$y=4x+16$

Aufgrund der Symmetrie muss $W^*$ ebenso wie $W$ auf der $x$ -Achse liegen:

$\begin{array}[t]{rll} 0&=& 4\cdot x+16 &\quad \scriptsize \mid\; -16\\[5pt] -16&=& 4\cdot x &\quad \scriptsize \mid\; :4\\[5pt] -4&=&x \end{array}$

$W^*(-4\mid 0)$

Wegen der Spiegelung an der Achse $a$ haben die beiden Wendepunkte $W$ und $W^*$ den gleichen Abstand zur Spiegelachse. Somit liegt $a$ genau in der Mitte zwischen den beiden Wendestellen.

$\begin{array}[t]{rll} a&=& \dfrac{-4+2}{2}& \\[5pt] a&=& -1 \end{array}$

Lösung A 1.2

Periode von $f_a$ berechnen:

Aus der Formel $p=\dfrac{2\pi}{b}$ folgt für $f_a$ :

$\begin{array}[t]{rll} p&=& \dfrac{2\pi}{a\cdot\pi}& \\[5pt] &=&\dfrac{2}{a} \end{array}$

Flächeninhalt des Dreiecks berechnen:

Da die Periode $p=\dfrac{2}{a}$ beträgt, haben zwei Tiefpunkte einen Abstand von $\dfrac{2}{a}.$ Die Höhe des Dreiecks entspricht der doppelten Amplitude, also $h=2a.$ Somit folgt:

$\begin{array}[t]{rll} A&=& \dfrac{1}{2} \cdot\dfrac{2}{a} \cdot 2a& \\[5pt] &=&2 \end{array}$

Der Flächeninhalt $A$ des Dreiecks ist demnach unabhängig von $a.$

Rechenweg anzeigen

$4 a^4 - 4a^2 +1=0$

Anwenden der Substitution mit $z=a^2$ :

$\begin{array}[t]{rll} z_{1,2}&=&\dfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot4\cdot1}}{2\cdot 4} & \\[5pt] &=&\dfrac{4\pm0}{8} & \\[5pt] &=&\dfrac{1}{ 2} & \\[5pt] \end{array}$

Rücksubstitution mit $z=\dfrac{1}{2}$ :

$\begin{array}[t]{rll} \dfrac{1}{2}&=&a^2 &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt] \pm\sqrt{\dfrac{1}{2}}&=&a \end{array}$

Da $a>0$ gelten soll, folgt also: $a=\sqrt{\dfrac{1}{2}}$

1. Schritt: Ortskurve bestimmen

Aus den Koordinaten von $H_a$ folgt $x=\dfrac{1}{2a}$ und somit $a=\dfrac{1}{2x}.$

Da $y=a$ gilt, ergibt sich $y=\dfrac{1}{2x}$ als eine Gleichung von K.

2. Schritt: Wert von $a$ bestimmen

Da die Tangente am gesuchten Punkt parallel zu $y=-2x$ sein soll, muss die Tangentensteigung ebenfalls $-2$ betragen.

$\(\begin{array}[t]{rll} K$

Aus $a=\dfrac{1}{2x}$ folgt:

$\begin{array}[t]{rll} a_1&=&\dfrac{1}{2\cdot(-\dfrac{1}{2})} & \\[5pt] &=&-1 \end{array}$

$\begin{array}[t]{rll} a_2&=&\dfrac{1}{2\cdot\dfrac{1}{2}} & \\[5pt] &=&1 \end{array}$

Da $a\gt 0$ gelten soll, folgt also $a=1$ als einzige Lösung.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?