Analytische Geometrie

Aufgabe II 1

Gegeben sind die Punkte $A(5 \mid -5 \mid 12),$ $B(5 \mid 5 \mid 12)$ und $C(-5 \mid 5 \mid 12).$

Zeige, dass das Dreieck $ABC$ gleichschenklig ist.

(2 BE)

Begründe, dass $A,$ $B$ und $C$ Eckpunkte eines Quadrats sein können, und gib die Koordinaten des vierten Eckpunkts $D$ dieses Quadrats an.

(3 BE)

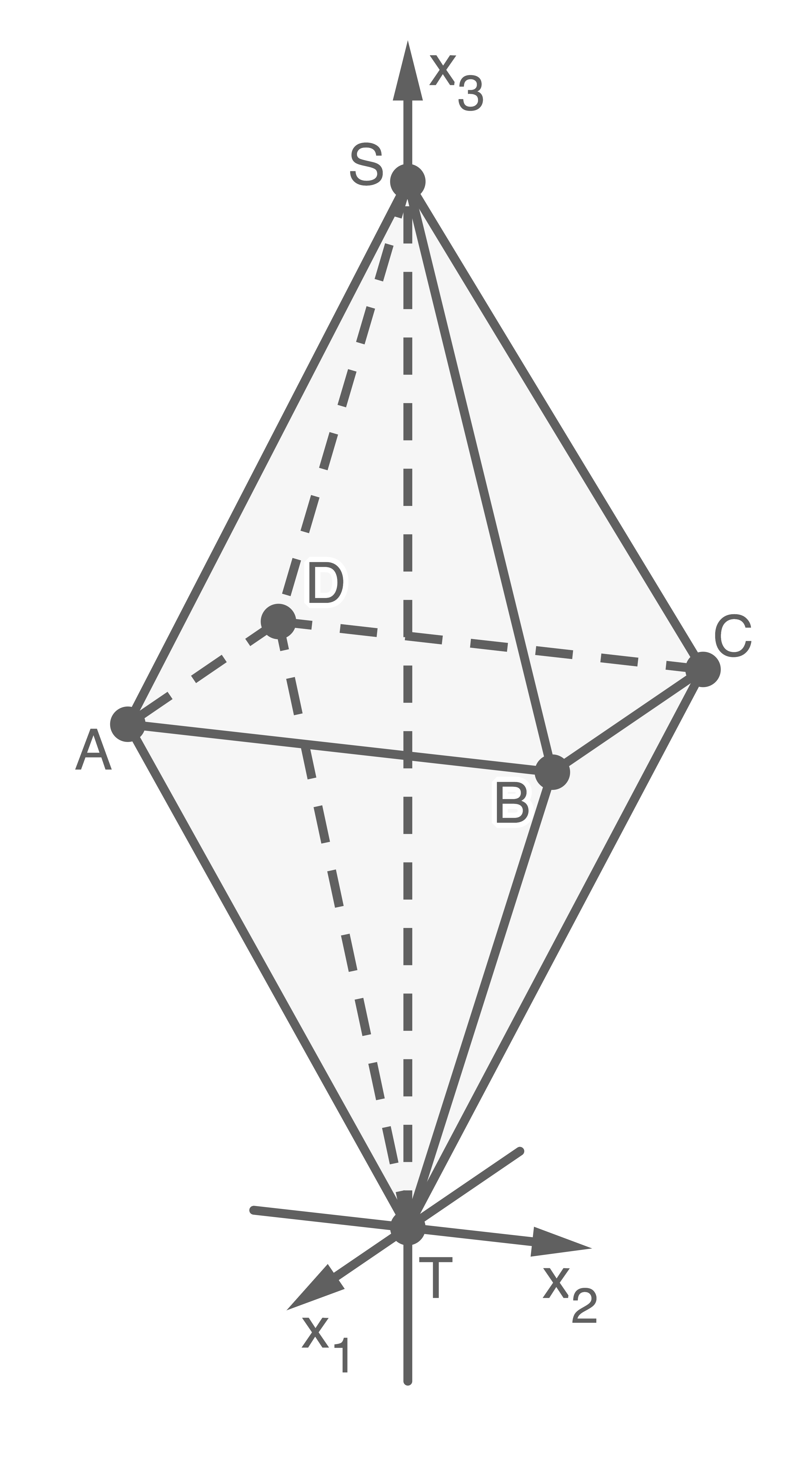
Im Folgenden wird die abgebildete Doppelpyramide betrachtet. Die beiden Teilpyramiden $ABCDS$ und $ABCDT$ sind gleich hoch.
Der Punkt $T$ liegt im Koordinatenursprung, der Punkt $S$ ebenfalls auf der $x_3$ -Achse.
Die Seitenfläche $BCT$ liegt in einer Ebene $E.$

Neues Abi BaWü 2024 Teil B Doppelpyramide

Ermittle den Flächeninhalt des Dreiecks $BCT.$

(3 BE)

Bestimme die Größe des Winkels, den die Seitenfläche $BCT$ mit der Fläche $ABCD$ einschließt.

(3 BE)

$E$ gehört zur Schar der Ebenen $E_k : kx_2 -5x_3 = 5k-60$ mit $k \in \mathbb{R}.$

Alle Ebenen der Schar schneiden sich in einer Gerade. Weise nach, dass die Kante $\overline{BC}$ auf dieser Geraden liegt.

(2 BE)

Ermittle diejenigen Werte von $k,$ für die $E_k$ mit der Seitenfläche $ADS$ mindestens einen Punkt gemeinsam hat.

(4 BE)

Die Seitenfläche $ADT$ liegt in der Ebene $F.$ Gib einen Normalenvektor von $F$ an und begründe deine Angabe, ohne die Koordinaten von $A$ und $D$ zu verwenden.
Bestimme denjenigen Wert von $k,$ für den $E_k$ senkrecht zu $F$ steht.

(4 BE)

Die Doppelpyramide wird so um die $x_1$ -Achse gedreht, dass die bisher mit $BCT$ bezeichnete Seitenfläche in der $x_1x_2$ -Ebene liegt und der bisher mit $S$ bezeichnete Punkt eine positive $x_2$ -Koordinate hat.
Bestimme diese $x_2$ -Koordinate und veranschauliche dein Vorgehen durch eine Skizze.

(4 BE)

Aufgabe II 2

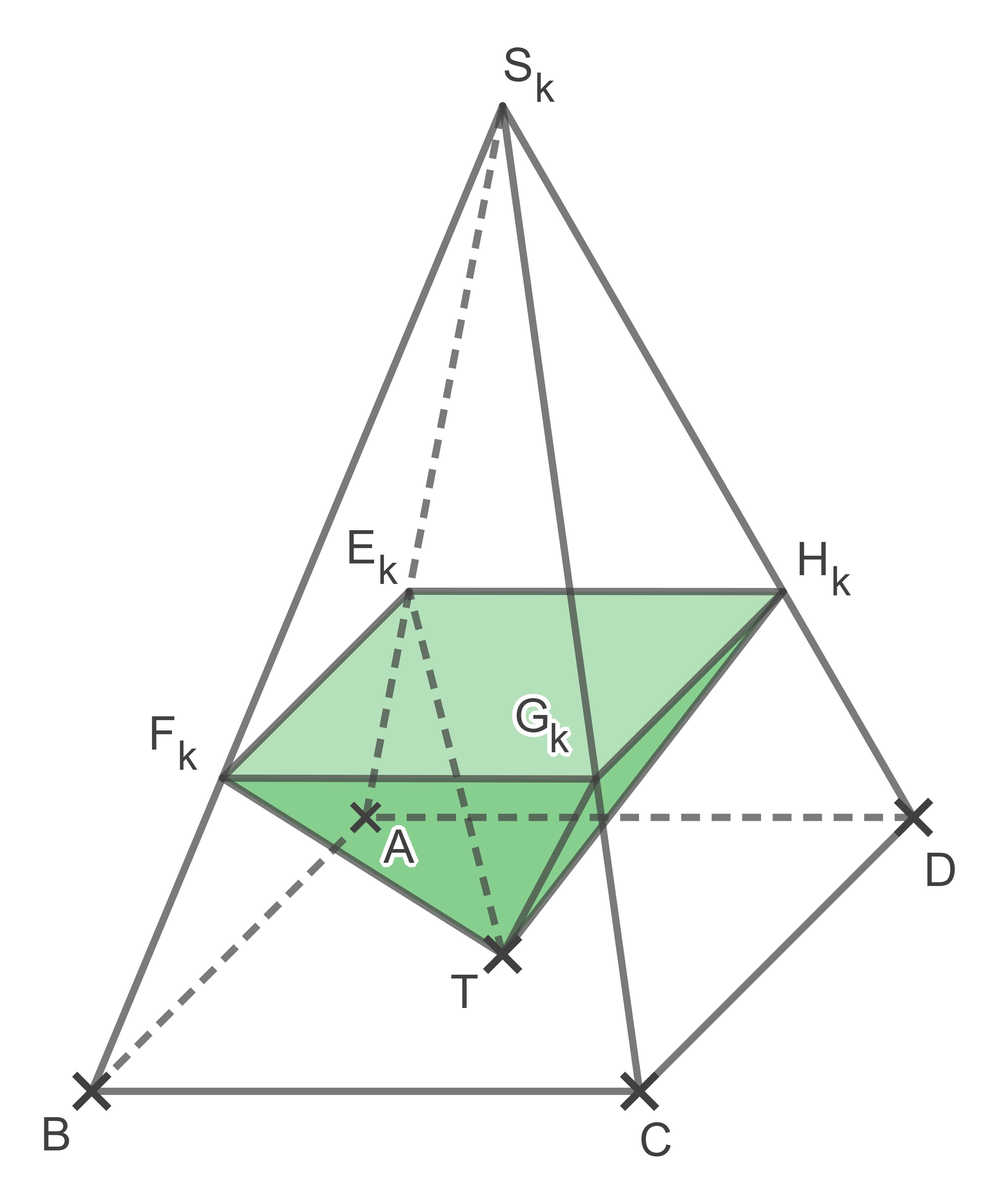
Betrachtet werden die Pyramiden $ABCDS_k$ mit $A(0\mid 0\mid0)$ , $B(2\mid0\mid0)$ , $C(2\mid2\mid0)$ , $D(0\mid2\mid0)$ und $S_k(1\mid 1\mid k)$ mit $k\gt1.$
Die gemeinsame Grundfläche $ABCD$ dieser Pyramiden ist quadratisch. Der Schnittpunkt der Diagonalen der Grundfläche $ABCD$ wird mit $T$ bezeichnet.
Die Abbildung zeigt beispielhaft eine dieser Pyramiden.

Diagramm eines geometrischen Körpers mit verschiedenen Punkten und Linien, die eine dreidimensionale Struktur darstellen.

Berechne den Inhalt der Oberfläche der Pyramide $ABCDS_k.$

(5 BE)

Der Punkt $S_k$ wird am Punkt $C$ gespiegelt.
Gib die Koordinaten des Spiegelpunktes zu $S_k$ an.
Berechne den Wert von $k$ so, dass $S_k$ zu seinem Spiegelpunkt den Abstand $6$ hat.

(4 BE)

Die Seitenfläche $ABS_k$ liegt in der Ebene $L$ .
Bestimme eine Gleichung von $L$ in Koordinatenform.
[zur Kontrolle: $k \cdot y-z=0$ ]

(3 BE)

Bestimme denjenigen Wert von $k$ , für den die Seitenfläche $ABS_k$ gegenüber der Grundfläche $ABCD$ um einen Winkel der Größe $60^{\circ}$ geneigt ist.

(3 BE)

Untersuche, ob es einen Wert für $k \gt 1$ gibt, sodass das Dreieck $BS_kD$ rechtwinklig ist.

(3 BE)

Die Ebene mit der Gleichung $z=1$ schneidet die vier vom Punkt $S_k$ ausgehenden Kanten der Pyramide $ABCDS_k$ in den Punkten $E_k$ , $F_k$ , $G_k$ und $H_k$ (vgl. Abbildung).

Bestimme die $x$ - und die $y$ -Koordinate von $F_k$ .

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung II 1

Ein Dreieck ist gleichschenklig, wenn zwei Seiten des Dreiecks gleich lang sind. Hier gilt:

$\left| \overrightarrow{AB} \right| = \left| \pmatrix{0 \\ 10 \\0} \right| = \sqrt{0^2+ 10^2 +0^2}$ $= 10$

$\left| \overrightarrow{BC} \right| = \left| \pmatrix{-10 \\ 0 \\0} \right| = \sqrt{(-10)^2+ 0^2 +0^2}$ $= 10$

Da die Vektoren gleich lang sind, handelt es sich um ein gleichschenkliges Dreieick.

Wenn das Skalarprodukt zweier Vektoren gleich $0$ ist, bilden sie einen rechten Winkel.

$\overrightarrow{AB} \circ \overrightarrow{BC} = \pmatrix{0 \\ 10 \\0} \circ \pmatrix{-10 \\ 0 \\0}$ $= 0 \cdot (-10) + 10 \cdot 0+ 0\cdot 0$ $= 0$

Damit bilden die Vektoren einen rechten Winkel. Da die Vektoren zudem noch gleich lang sind (siehe Aufgabe a)), können die Punkte $A$ , $B$ und $C$ die Eckpunkte eines Quadrats sein.

Der Punkt $D$ entspricht dem um den Vektor $\overrightarrow{BC}$ verschobenen Punkt $A$ . Der Punkt $A\left(5\mid -5\mid 12\right)$ muss also um $-10$ entlang der $x_1$ -Achse verschoben werden. Damit ergibt sich $D\left(-5\mid-5\mid12\right)$ .

Für die Grundseite $\overline{BC}$ des Dreiecks gilt:

$\left| \overrightarrow{BC}\right| = \left|\pmatrix{-10\\0\\0}\right| = 10$

Zudem gilt:

$\overrightarrow{TB} = \overrightarrow{OB} = \pmatrix{5\\5\\12}$

$\overrightarrow{TC} = \overrightarrow{OC} = \pmatrix{-5\\5\\12}$

Da die Beträge der Einträge der Vektoren gleich sind, sind $\overline{TB}$ und $\overline{TC}$ gleich lang, sodass es sich bei $BCT$ um ein gleichschenkliges Dreieck handelt.

Die Höhe zur Grundseite $\overline{BC}$ verläuft daher durch den Mittelpunkt $M$ von $\overline{BC}:$

$\overrightarrow{OM} = \frac{1}{2}\cdot \left(\overrightarrow{OB}+\overrightarrow{OC} \right)$ $= \frac{1}{2}\cdot \left( \pmatrix{5\\5\\12}+ \pmatrix{-5\\5\\12} \right)=\pmatrix{0\\5\\12}$

Die Höhe des Dreiecks ergibt sich damit zu:

$\left|\overrightarrow{TM}\right| = \left|\pmatrix{0\\5\\12}-\pmatrix{0\\0\\0}\right|$ $=\sqrt{0^2 +5^2+12^2}=\sqrt{169}=13$

Für den Flächeninhalt des Dreiecks $BCT$ folgt:

$\begin{array}[t]{rll} A_{\Delta BCT}&=&\frac{1}{2}\cdot \left|\overrightarrow{BC}\right|\cdot\left|\overrightarrow{TM}\right| \\[5pt] &=&\frac{1}{2}\cdot 10\cdot 13 = 65\text{ [FE]} \end{array}$

Der Winkel der beiden Ebenen entspricht gerade dem Winkel zwischen $\overrightarrow{BT}$ und $\overrightarrow{BA}$ . Dieser lässt sich wie folgt berechnen:

Vollständigen Rechenweg anzeigen

$\alpha \approx 67,4°$

Damit beträgt der gesuchte Winkel etwa $67,4°.$

Die Kante $\overline{BC}$ liegt auf dieser Geraden, wenn beide Punkte $B$ und $C$ in jeder der Ebenen $E_k$ liegen. Einsetzen der Koordinaten von $B$ in die Ebenengleichung von $E_k$ liefert:

Vollständigen Rechenweg anzeigen

$... -60 = -60$

Für die Koordinaten von $C$ folgt:

Vollständigen Rechenweg anzeigen

$... -60 = 60$

Unabhängig von $k$ liegen die Punkte $B$ und $C$ also in der Ebene $E_k.$ Damit liegt die Kante $\overline{BC}$ ebenfalls in jeder der Ebenen $E_k$ und somit auf der gemeinsamen Gerade aller Ebenen $E_k.$

Aus Teilaufgabe e) ist bekannt, dass die Kante $\overline{BC}$ in jedem Fall in der Ebene $E_k$ liegt.
Damit $E_k$ die Seitenfläche $ADS$ schneidet, muss sie die $x_3$ -Achse daher zwischen der Fläche $ABCD$ und dem Punkt $S$ schneiden.
Für Punkte auf der $x_3$ -Achse gilt $x_1=0$ und $x_2=0.$ Einsetzen in die Ebenengleichung:

Vollständigen Rechenweg anzeigen

$x_3 = 12-k$

Der Schnittpunkt von $E_k$ mit der $x_3$ -Achse hat die Koordinaten $S_k\left(0\mid0\mid12-k\right).$

Damit der Schnittpunkt im Punkt $S$ liegt, muss gelten:

$\begin{array}[t]{rll} x_3 &=& 24 \\[5pt] 12-k &=& 24 &\quad \scriptsize \mid\; -12 \\[5pt] -k &=& 12 &\quad \scriptsize \mid\; \cdot (-1) \\[5pt] k &=& -12 \end{array}$

Für $k=-12$ schneidet die Ebene $E_k$ die $x_3$ -Achse also im Punkt $S.$
Für die Fläche $ABCD$ gilt $x_3=12:$

$\begin{array}[t]{rll} x_3 &=& 12 \\[5pt] 12-k &=& 12 &\quad \scriptsize \mid\;-12 \\[5pt] -k &=& 0 \\[5pt] k &=& 0 \end{array}$

Für $k=0$ liegt der Schnittpunkt von $E_k$ mit der $x_3$ -Achse also in der Fläche $ABCD.$
Insgesamt besitzt die Ebene $E_k$ für $-12\leq k \leq 0$ mindestens einen gemeinsamen Punkt mit der Seitenfläche $ADS.$

Normalenvektor bestimmen und begründen
Die Seitenfläche $ADT$ entsteht durch Spiegelung der Seitenfläche $BCT$ an der $x_1x_3$ -Ebene. Dementsprechend entsteht auch $F$ durch Spiegelung von $E$ an der $xz$ -Ebene.
Ein Normalenvektor von $E$ ist $\pmatrix{0\\12\\-5}.$ Durch den Faktor $-1$ vor der $x_2$ -Koordinate entsteht eine Spiegelung an der $x_1x_3$ -Ebene. Also ist ein Normalenvektor von $F:$

$\overrightarrow{n_F}=\pmatrix{ 0\\-12 \\-5 }$

Parameterwert bestimmen
Die zwei Ebenen $F$ und $E_k$ stehen senkrecht zueinander, wenn das Skalarprodukt ihrer Normalenvektoren gleich null ist.

Vollständigen Rechenweg anzeigen

$k = \frac{25}{12}$

Für $k=\frac{25}{12}$ steht die Ebene $E_k$ senkrecht zur Ebene $F.$

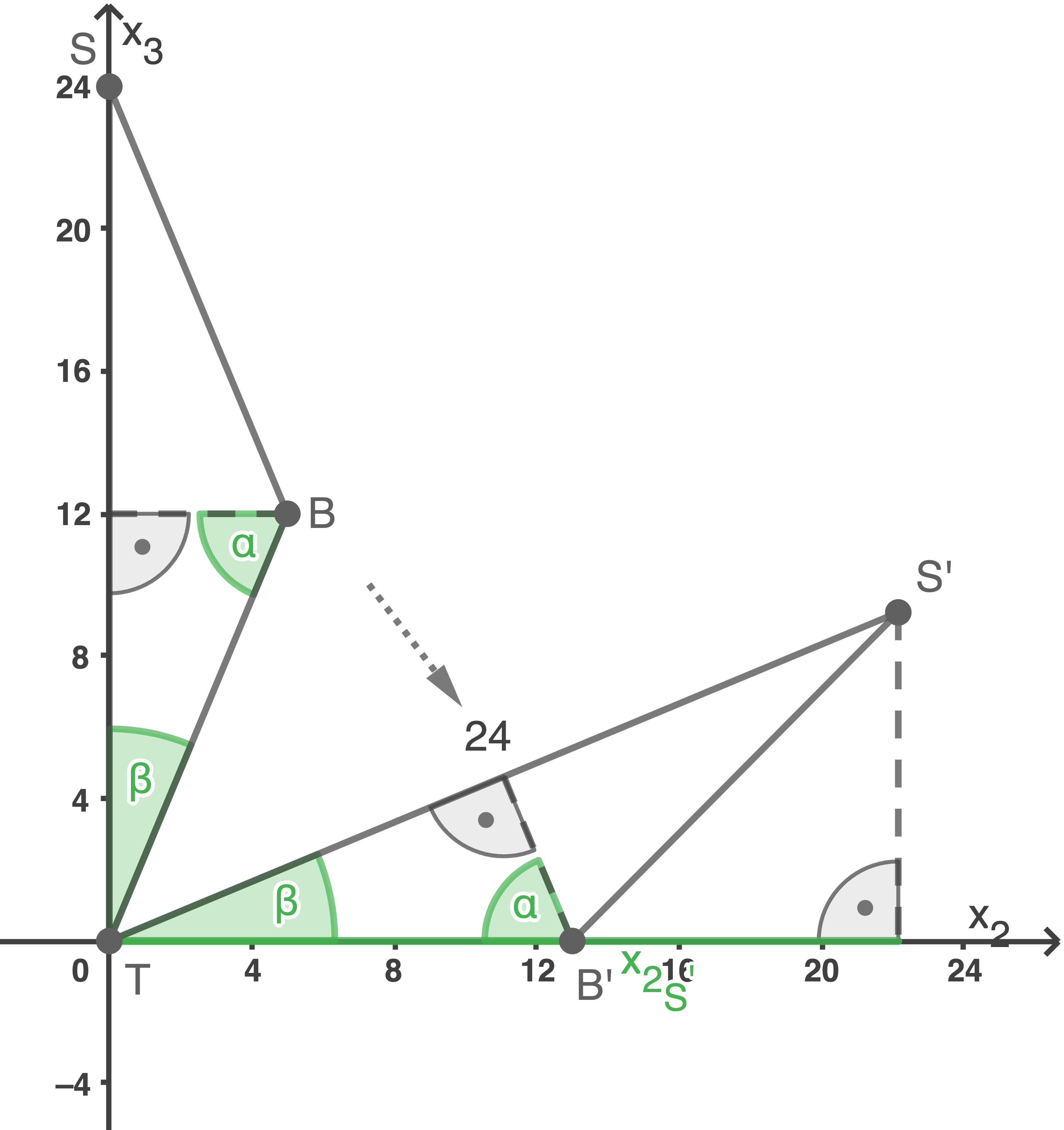
Neues Abi BaWü 2024 Teil B Doppelpyramide Drehung

$\alpha$ entspricht dem Winkel aus Teilaufgabe d).
Es gilt:

$\(\cos \beta =\frac{x_{2_{S$

Für $\beta$ gilt aufgrund der Winkelsumme im Dreieck:

Vollständigen Rechenweg anzeigen

$\beta \approx 22,6^{\circ}$

Einsetzen in die erste Gleichung:

Vollständigen Rechenweg anzeigen

$\( y_{S$

Die neue $x_2$ -Koordinate des bisher mit $S$ bezeichneten Punkts, lautet $\(x_{2_{S$

Lösung II 2

$\overrightarrow{AB}= \pmatrix{2\\0\\0}$ , $\mid \overrightarrow{AB} \mid = 2\,[\text{LE}]$
Da die Grundfläche der Pyramide quadratisch ist, kann der Flächeninhalt der Grundfläche berechnet werden durch $\mid \overrightarrow{AB} \mid^2 =2^2 =4\,[\text{FE}].$
Die Koordinaten des Mittelpunkts der Strecke $\overline{AB}$ sind gegeben durch $Z(1 \mid 0 \mid 0).$ Es gilt also $\overrightarrow{ZS}=\pmatrix{0\\1\\k}$ und damit insbesondere $\mid \overrightarrow{ZS} \mid=\sqrt{0^2+1^2+k^2}$ $=\sqrt{1+k^2}[\text{LE}].$
Der Flächeninhalt der Oberfläche der Pyramide ist gegeben durch die Summe des Flächeninhalts der Grundfläche und der vier Seitenflächen:
$4 +4 \cdot \dfrac{1}{2} \cdot 2 \cdot \sqrt{1+k^2} =$ $4+4\cdot \sqrt{1+k^2}\,[\text{FE}]$
Der Inhalt der Oberfläche der Pyramide ist gegeben durch $4+4\cdot \sqrt{1+k^2}\,[\text{FE}].$

$\(\overrightarrow{OS_k$ $=\pmatrix{2\\2\\0}+\pmatrix{2-1\\2-1\\0-k}=\pmatrix{3\\3\\-k}$

Die Koordinaten des Spiegelpunktes sind gegeben durch $\(S$

Gesucht ist nun der Wert für $k,$ sodass $\(\mid \overrightarrow{S_kS$ gilt.
$\(\overrightarrow{S_kS$

$\(\mid \overrightarrow{S_kS$ $=\sqrt{8+4k^2}$

Damit muss gelten

$\begin{array}[t]{rll} 6&=& \sqrt{8+4k^2}&\quad \scriptsize \mid ()^2\; \\[5pt] 36&=& 8+4k^2&\quad \scriptsize \mid -8\; \\[5pt] 28&=& 4k^2&\quad \scriptsize \mid :4\; \\[5pt] 7&=& k^2&\quad \scriptsize \mid \sqrt{} \; \\[5pt] \sqrt{7}&=&k \end{array}$

Für $k=\sqrt{7}$ hat $S_k$ zu seinem Spiegelpunkt den Abstand $6.$

Für den Normalenvektor $\overrightarrow{n}$ zu $L$ müssen die Gleichungen $\overrightarrow{n} \circ \overrightarrow{AB}=0$ und $\overrightarrow{n} \circ \overrightarrow{AS_k}=0$ gelten.

$\overrightarrow{n} \circ \overrightarrow{AB}=\pmatrix{n_1\\n_2\\n_3} \circ \pmatrix{2\\0\\0}$ $=2\cdot n_1\stackrel{!}{=}0$

$\overrightarrow{n} \circ \overrightarrow{AS_k}=\pmatrix{n_1\\n_2\\n_3} \circ \pmatrix{1\\1\\k}$ $=n_1+n_2+n_3\cdot k\stackrel{!}{=}0$

Die erste Gleichung liefert $n_1=0.$ Damit folgt für die zweite Gleichung

$\begin{array}[t]{rll} 0&=& n_2+n_3\cdot k &\quad \scriptsize \mid\;-n_2 \\[5pt] -n_2&=& n_3\cdot k &\quad \scriptsize \mid\;\cdot (-1)\\[5pt] n_2&=& -n_3\cdot k \end{array}$

Insgesamt ergibt sich damit der Normalenvektor $\overrightarrow{n}=\pmatrix{0\\k\\-1}.$

Damit gilt für die Gleichung von $L$ zunächst zunächst $L: 0\cdot x+k \cdot y + (-1)\cdot z$ $=k \cdot y-z=c.$

$L$ enthält nach Definition den Punkt $A$ und damit den Koordinatenursprung.

Einsetzten dieses Punktes in $L$ liefert schließlich die Gleichung $L:k \cdot y-z=0.$

Der Normalenvektor zur Grundfäche der Pyramide ist gegeben durch $\overrightarrow{m}=\pmatrix{0\\0\\1}.$

Der Normalenvektor der Fläche $ABS_k$ ist nach Teilaufgabe c) gegeben durch $\overrightarrow{n}=\pmatrix{0\\k\\-1}.$

Gesucht ist die Lösung der Gleichung

Vollständigen Rechenweg anzeigen

$\cos(60^{\circ})=\dfrac{1}{\sqrt{k^2+1}}$

Mit $\cos(60^{\circ})=\dfrac{1}{2}$ gilt:

Vollständigen Rechenweg anzeigen

$k=\sqrt{3}$

Für $k=\sqrt{3}$ ist die Seitenfläche $ABS_k$ gegenüber der Grundfläche um einen Winkel der Größe $60^{\circ}$ geneigt.

Das Dreieck $BS_kD$ kann höchstens am Punkt $S_k$ rechtwinklig sein. Dafür muss $\overrightarrow{BS_k}\circ \overrightarrow{DS_k}=0$ gelten.

$\overrightarrow{BS_k}=\pmatrix{1-2\\1-0\\k-0}=\pmatrix{-1\\1\\k}$

$\overrightarrow{DS_k}=\pmatrix{1-0\\1-2\\k-0}=\pmatrix{1\\-1\\k}$

$\overrightarrow{BS_k} \circ \overrightarrow{DS_k}=\pmatrix{-1\\1\\k} \circ \pmatrix{1\\-1\\k}$ $=-1\cdot 1 + 1 \cdot (-1) +k\cdot k)$ $=-2+k^2$

$\begin{array}[t]{rll} 0&=& -2+k^2 &\quad \scriptsize \mid\;+2 \\[5pt] 2&=& k^2 &\quad \scriptsize \mid\;\sqrt{}\\[5pt] \sqrt{2}&=& k \end{array}$

Damit ist das Dreieck für $k=\sqrt{2}$ rechtwinklig.

Die Koordinaten des Punktes $F_k$ lassen sich durch die Gleichung $\overrightarrow{OB}+t \cdot \overrightarrow{BS_k}=\pmatrix{x\\y\\1}$ berechnen.

$\pmatrix{2\\0\\0}+t\cdot \pmatrix{-1\\1\\k}=\pmatrix{x\\y\\1}$

Die letzte Zeile liefert $t=\dfrac{1}{k}.$ Damit folgt aus der zweiten Zeile $y=\dfrac{1}{k}.$ Aus der ersten Zeile lässt sich schließlich $x=2-\dfrac{1}{k}$ berechnen.

Der Punkt $F_k$ hat die Koordinaten $(2-\dfrac{1}{k}\mid \dfrac{1}{k}\mid 1).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?