Wahlteil A1

Aufgabe A1.1

Betrachtet wird das Wachstum einer Palme.
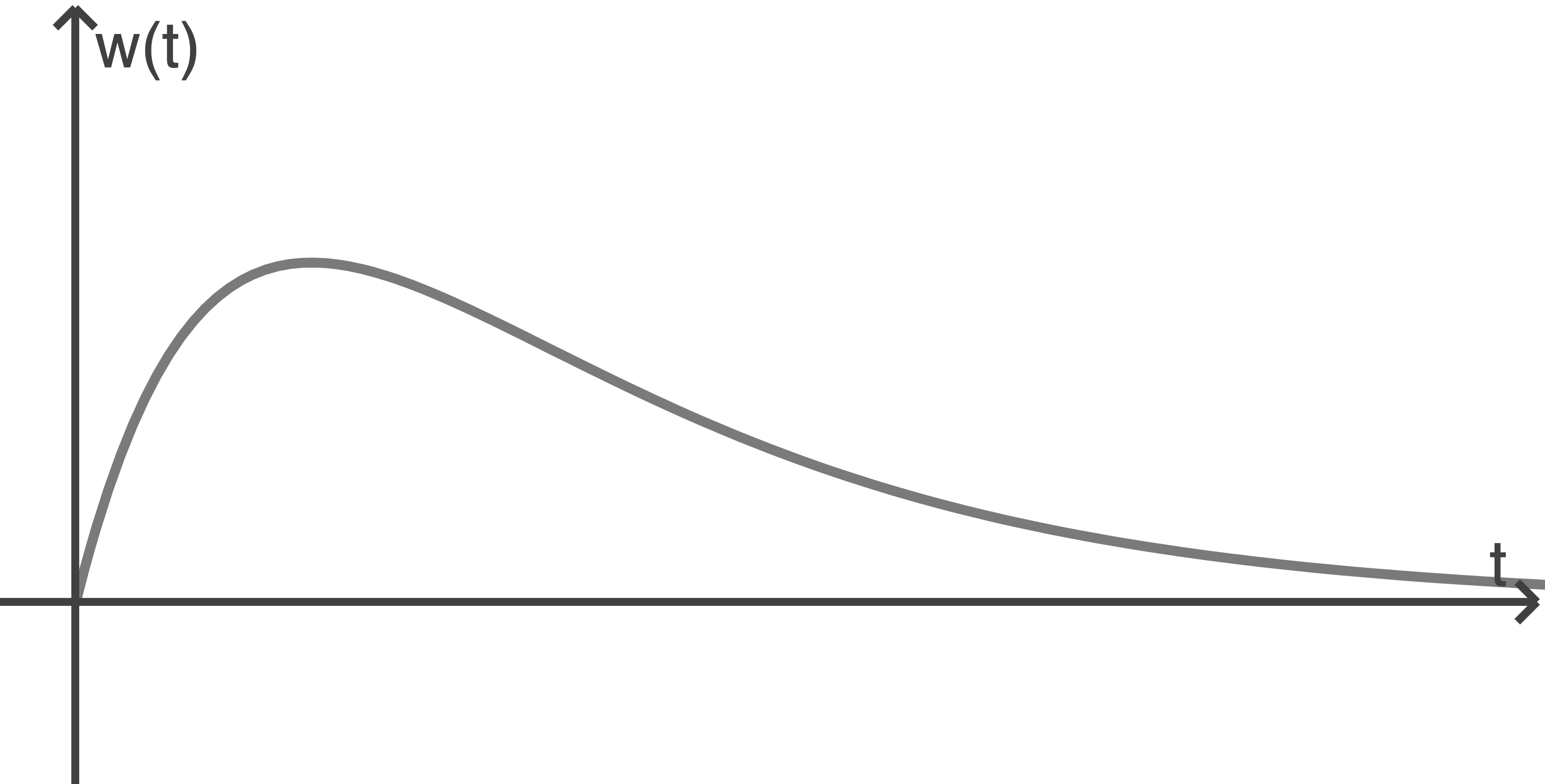
Ihre Höhe beträgt zu Beobachtungsbeginn einen Meter, die momentane Wachstumsrate ihrer Höhe wird durch die Funktion $w$ mit $w(t)=4\cdot (\mathrm e^{-t}- \mathrm e^{-2t})$ ; $\,t\geq0$
( $t$ in Jahren nach Beobachtungsbeginn, $w(t)$ in Metern pro Jahr) beschrieben.

Die Abbildung zeigt den Graphen von $w$ .

Grafik eines Zeitverlaufes mit einer Kurve für w(t), die ansteigt und dann abfällt.

Gib die momentane Wachstumsrate zum Zeitpunkt $t=1$ an.
Begründe anhand des Graphen, dass die Höhe der Palme im abgebildeten Zeitraum nie abnimmt.
Die Funktion $w$ besitzt im abgebildeten Bereich eine Wendestelle.

Beschreibe die Bedeutung dieser Wendestelle im Sachzusammenhang.

Berechne den Zeitpunkt der maximalen momentanen Wachstumsrate.

(4 VP)

Berechne die Höhenzunahme der Palme im zweiten Jahr nach Beobachtungsbeginn.
Bestimme einen integralfreien Funktionsterm der Funktion $h$ , der die Höhe der Palme zum Zeitpunkt $t$ angibt.

Ermittle rechnerisch den Zeitpunkt, an dem die Palme eine Höhe von $1,50 \,m$ hat.

Untersuche, welche Höhe die Palme maximal erreichen kann.

Formuliere eine Fragestellung im Sachzusammenhang, die auf die Gleichung $\dfrac{h(t+0,5)}{h(t)}=1,5$ führt.

(8 VP)

Aufgabe A1.2

Für jeden Wert $a\gt 0$ ist eine Funktion $f_a$ gegeben durch $f_a(x)=-\dfrac{1}{8}x^4+a^2x^2$ .

Abgebildet sind drei Graphen.

Begründe, dass zwei dieser Graphen nicht zu einer Funktion $f_a$ gehören.
Der verbleibende Graph gehört zu einer Funktion $f_a$ .

Bestimme den zugehörigen Wert von $a$ .

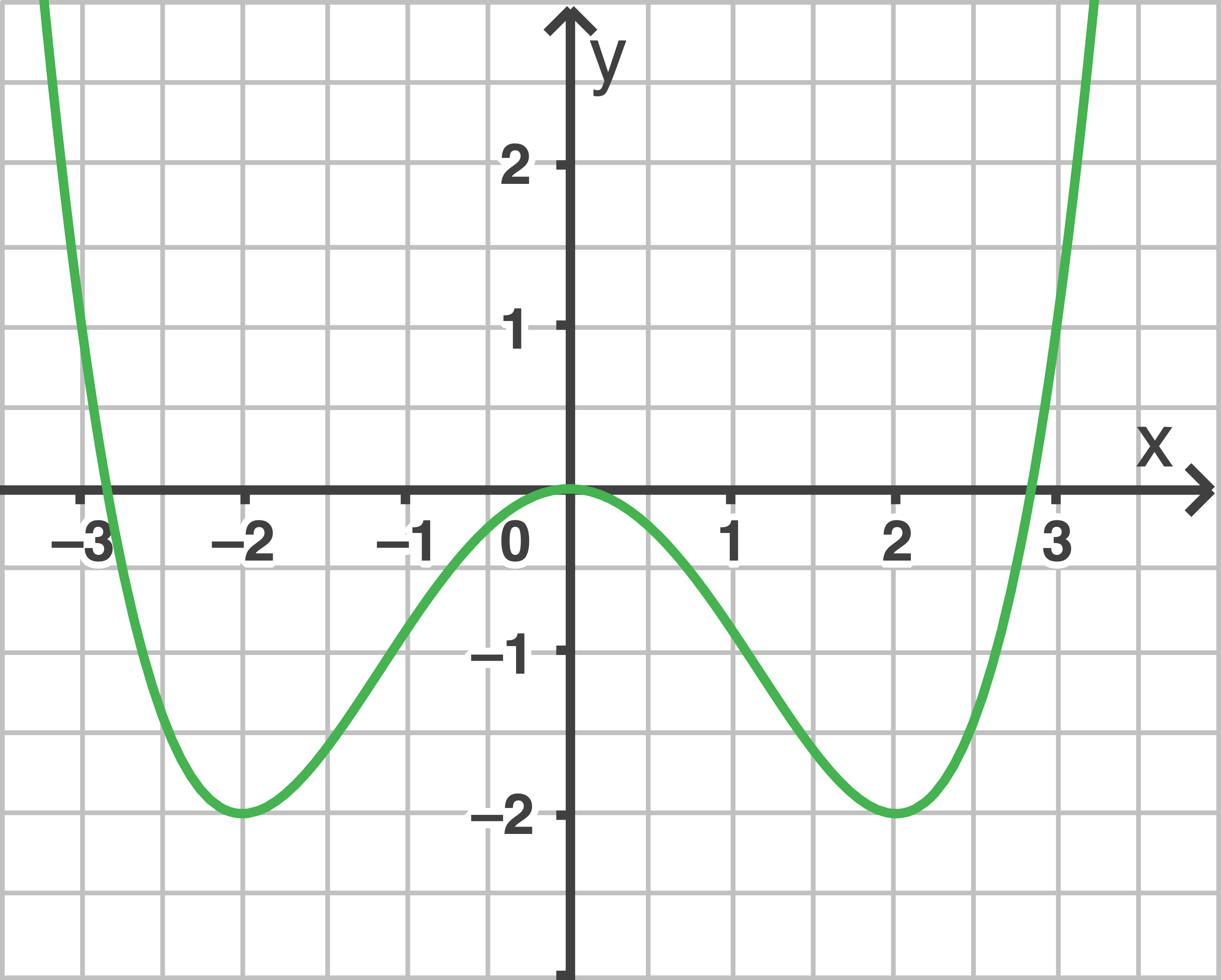
Graph einer quadratischen Funktion im Koordinatensystem mit grüner Kurve.

Abb. 1

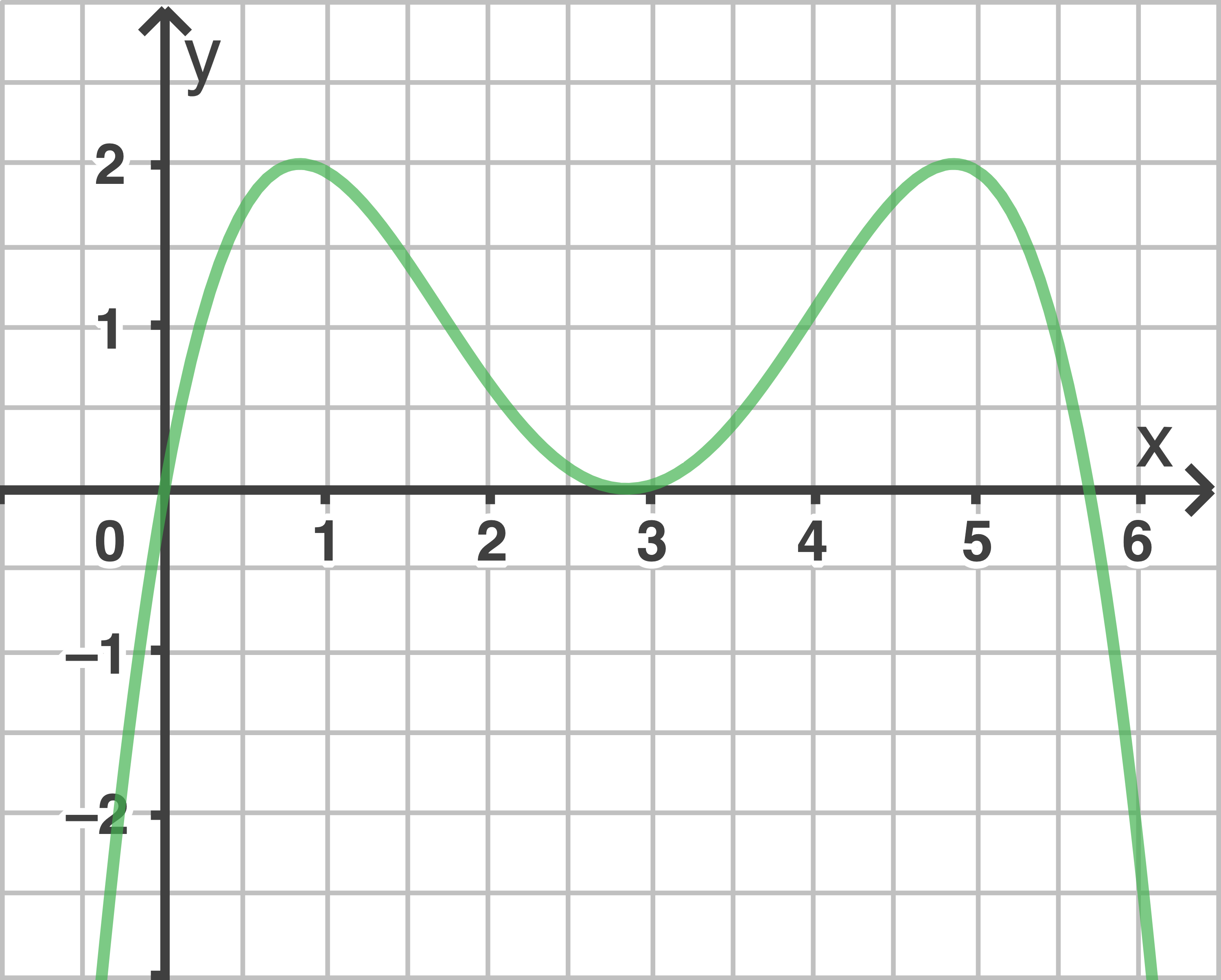
Graph einer Funktion im Koordinatensystem mit grüner Linie und Gitterlinien.

Abb. 2

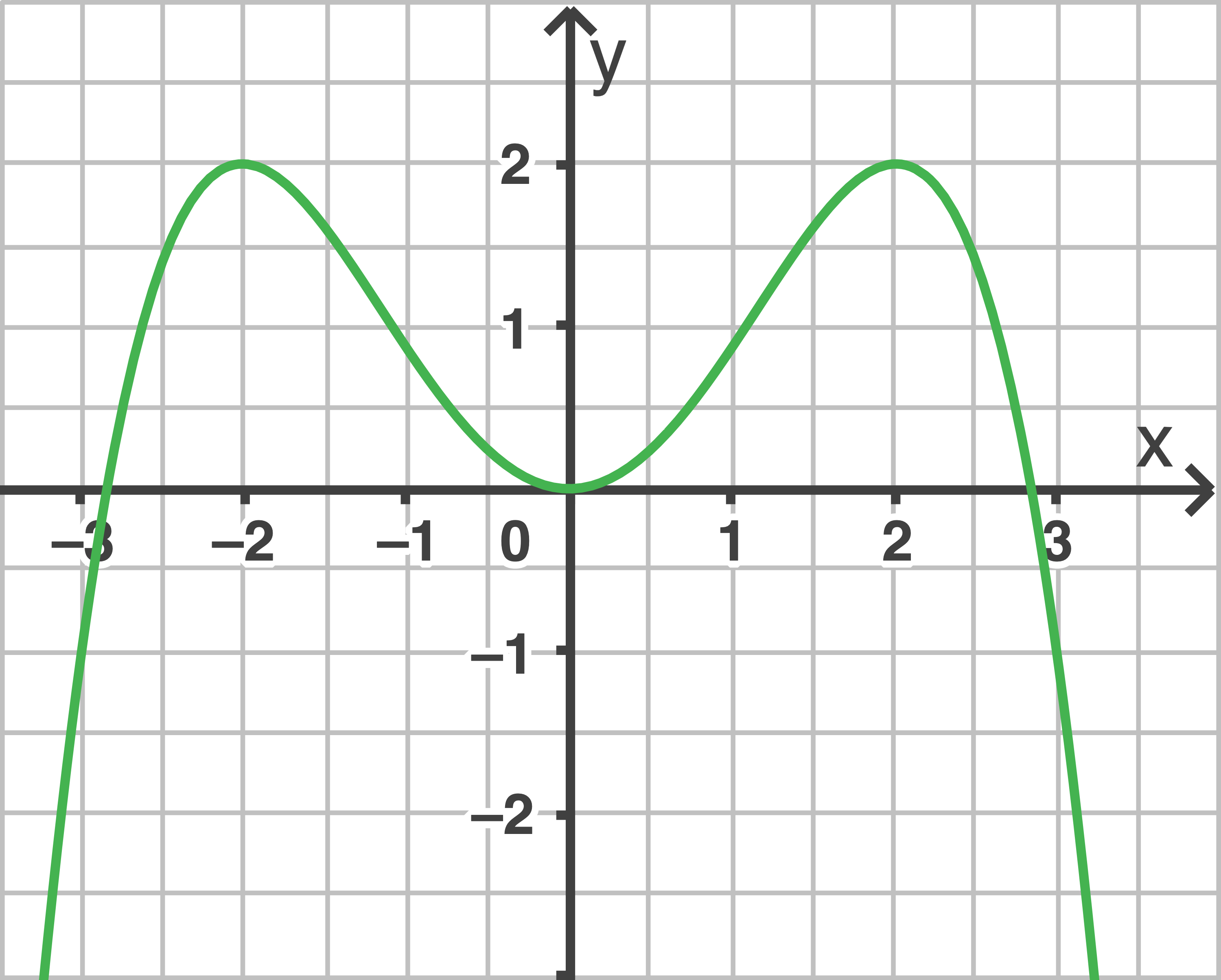
Graf einer mathematischen Funktion im Koordinatensystem mit einer grünen Kurve.

Abb. 3

(3 VP)

Jede Funktion $f_a$ besitzt an der Stelle $x_1=2a$ ein Maximum.
Ermittle eine Gleichung der Kurve, auf der die zugehörigen Hochpunkte aller Graphen von $f_a$ liegen.

(2 VP)

Der Punkt $O\, (0 \mid 0)$ sowie die Punkte $P\, (4a \mid -16a^{4})$ und $Q\, (-4a \mid -16a^{4})$ des Graphen von $f_a$ bilden ein Dreieck.
Berechne denjenigen Wert von $a$ , für den dieses Dreieck gleichseitig ist.

(3 VP)

Lösung A1.1

Momentane Wachstumsrate
Die momentane Wachstumsrate zum Zeitpunkt $t=1$ beträgt $w(1)= 4 \cdot (\mathrm e^{-1} - \mathrm e^{-2\cdot 1}) \approx 0,93$ Meter pro Jahr.

Begründung, dass die Höhe der Palme im Zeitraum nie abnimmt
Die Höhe der Palme nimmt im abgebildeten Zeitraum nie ab, da der Graph der Funktion $w$ im abgebildeten Zeitraum nur oberhalb der $t$ -Achse verläuft. Somit ist die Wachstumsrate im abgebildeten Zeitraum stets positiv.

Bedeutung der Wendestelle im Sachzusammenhang
Die Wendestelle befindet sich im Punkt mit der größten negativen Steigung. Zu diesem Zeitpunkt nimmt die Wachstumsrate der Palme am stärksten ab.

Zeitpunkt der maximalen momentanen Wachstumsrate
Den Zeitpunkt der maximalen Wachstumsrate stellt die Stelle dar, an der die Funktion ein Maximum annimmt.

Erste Ableitung von $w(t):$
Die e-Funktion wird dabei so abgeleitet, dass mit der inneren Ableitung multipliziert wird.

$w(t)=4\cdot (\mathrm e^{-t}- \mathrm e^{-2t})$

$\(w$ $=4\left(-\mathrm e^{-t} +2 \mathrm e^{-2t}\right)$

Notwendiges Kriterium für Extremstellen:

$\(\begin{array}[t]{rll} w$

Die Wachstumsrate ist zum Zeitpunkt $t \approx 0,69$ maximal.

Höhenzunahme im zweiten Jahr berechnen

Der Flächeninhalt der vom Graphen der Funktion und der $x$ -Achse eingeschlossenen Fläche stellt die Höhenzunahme dar.

$\displaystyle\int_{1}^{2}w(t)\;\mathrm dt \approx 0,70$

Vollständige Lösung anzeigen

Die Höhenzunahme im zweiten Jahr beträgt ca. 0,7 Meter.

Integralfreien Funktionsterm bestimmen

Gesucht ist eine neue Funktion $h$ , welche die Höhe der Palme angibt. Die Höhe der Palme berechnest du durch Integration. Bei einem integralfreien Funktionsterm werden die Integrationsgrenzen in das Integral eingesetzt, um so die neue Funktion zu bestimmen.
Zum Zeitpunkt $t=0$ ist die Palme einen Meter groß. Die Funktion $h$ lautet folglich:

$h(t)= 3 -4\mathrm e^{-t} +2 \mathrm e^{-2t}$

Vollständige Lösung anzeigen

Zeitpunkt für Höhe ermitteln

$h(t)=1,5$

$\begin{array}[t]{rll} 3 -4\mathrm e^{-t} +2 \mathrm e^{-2t} &=& 1,5 \quad \scriptsize \mid \; -3 \mid\, :4 \\[5pt] - \mathrm e^{-t} +0,5 \cdot \mathrm e^{-2t} &=& -0,375 \quad \scriptsize \mid \; \cdot 2 \\[5pt] -2 \mathrm e^{-t}+ \mathrm e^{-2t} &=&-0,75 \end{array}$

Um die Gleichung nach $t$ aufzulösen, wird zunächst mit $\mathrm e^{-t}=u$ substituiert:

$\begin{array}[t]{rll} -2u+u^2 &=&-0,75 \quad \scriptsize \mid\;+0,75 \\[5pt] -2u+u^2+0,75&=&0 \\[5pt] u^2-2u+0,75&=&0 \end{array}$

Anwendung der $pq$ -Formel:

$\begin{array}[t]{rll} u_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt] &=&-\dfrac{-2}{2} \pm \sqrt{\left(\dfrac{-2}{2}\right)^2-0,75}\\[5pt] &=&1\pm\sqrt{0,25}\\[5pt] &=&1\pm 0,5\\[5pt] \end{array}$

Daraus folgen $u_1=0,5$ und $u_2=1,5.$

Resubstitution:

1) $\mathrm e^{-t}=0,5$

Daraus folgt $-t=\ln(0,5)$ und somit $t_1=-\ln(0,5)\approx 0,69$

2) $\mathrm e^{-t}=1,5$

Daraus folgt $-t=\ln(1,5)$ und somit $t_2=-\ln(1,5)\approx -0,41$

Da $t\geq 0$ ist $t_1=0,69$ die einzige Lösung.

Zum Zeitpunkt $t \approx 0,7$ hat die Palme eine Höhe von $1,5\,\text{m}.$

Maximale Höhe untersuchen

Dazu wird der Grenzwert der Funktion $h$ betrachtet.
Wegen $\mathrm e^{-t} \rightarrow 0$ für $t \rightarrow +\infty$ verläuft $h(t) \rightarrow 3$ .
Somit kann die Palme in dieser Modellierung eine maximale Höhe von $3\,\text{m}$ erreichen.

Fragestellung formulieren

„In welchem Halbjahreszeitraum nimmt die Höhe der Palme um 50 % zu?“

Lösung A1.2

Begründung für Zuordnung

Für $x \rightarrow \pm \infty$ gilt: $f_a(x) \rightarrow - \infty$ . Aus diesem Grund kann Abb. 1 ausgeschlossen werden.

Der Graph von $f_a$ ist achsensymmetrisch zur $y$ -Achse, da die Funktionsgleichung ganzrational mit geradzahligen Exponenten ist. Somit kann Abb. 2 ausgeschlossen werden.

Der Graph von $f_a$ entspricht Abb. 3.

Wert von $a$ bestimmen

In Abb. 3 können die Koordinaten eines Punktes (z.B. $(2\mid 2)$ ) abgelesen und in die Funktionsgleichung eingesetzt werden.

$f_a(x)= -\dfrac{1}{8} \cdot x^4 + a^2 \cdot x^2$

$\begin{array}[t]{rll} f_a(2)&=& 2&\quad \scriptsize \\[5pt] -\dfrac{1}{8} \cdot 2^4 +a^2 \cdot 2^2&=& 2&\quad \scriptsize \\[5pt] -2 +a^2 \cdot 4 &=&2\quad \scriptsize \mid +2 \mid :4\; \\[5pt] a&=&1 \end{array}$

Ortskurve ermitteln

Zunächst wird die $y$ -Koordinate des Hochpunkts berechnet:

$f_a(2a)=-\dfrac{1}{8} \cdot 16 a^4 +4a^4 =2a^4$

Aus $H (2a \mid 2a^4)$ ergibt sich $x=2a$ und $y=2a^4$ .

$x=2a$ nach $a$ aufgelöst und in $y=2a^4$ eingesetzt ergibt:

$y=2 \cdot \left(\dfrac{x}{2} \right)^4 = \dfrac{1}{8}x^4$

Ein Dreieck ist gleichseitig, wenn alle Seiten gleich lang sind. Zunächst werden die Längen zweier Seiten in Abhängigkeit von $a$ gleichgesetzt.

$\left|\overline{OP}\right| =\left|\overline{PQ}\right|$

Vollständigen Rechenweg anzeigen

$a=\sqrt[6]{\dfrac{3}{16}}$

Da $a= \sqrt[6]{\dfrac{3}{16}} \approx 0,76$ die einzige Lösung ist und in der Aufgabenstellung davon ausgegangen wird, dass es ein $a$ gibt, für das das Dreieck gleichseitig ist, ist damit gezeigt, dass für dieses $a$ das Dreieck gleichseitig ist.