Pflichtteil 2

Aufgabe 1

Gegeben ist die Funktion $f$ mit $f(x)=4x-x^2.$ Die Abbildung zeigt ihren Graphen $G_f$ sowie die Tangenten an $G_f$ in den Schnittpunkten mit der $x$ -Achse.

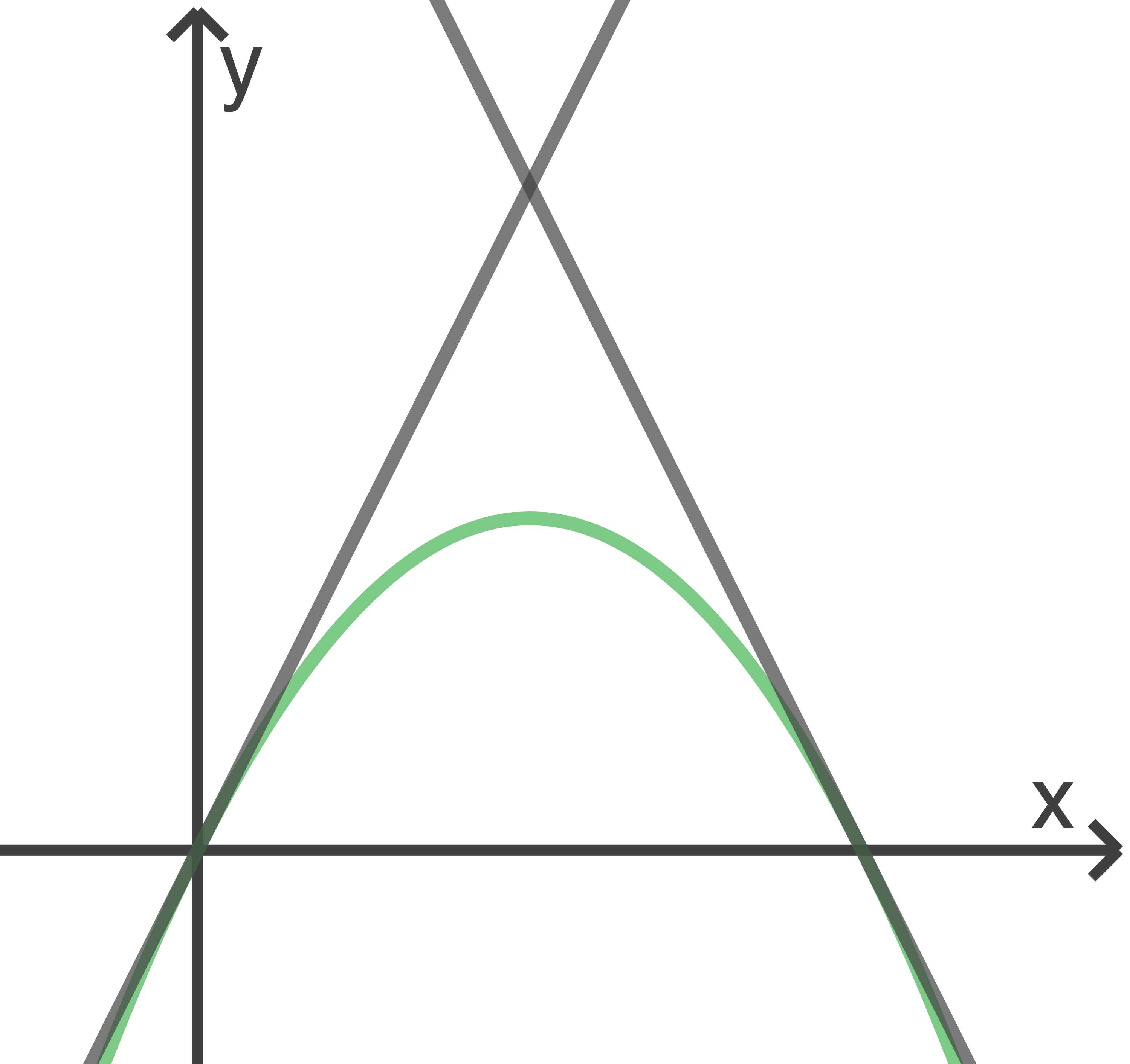
Grafik eines Koordinatensystems mit einer grünen Parabel und Achsenbeschriftungen.

Weise nach: Die Tangente an $G_f$ an der Stelle $x=0$ hat die Steigung 4.

(0,5 VP)

Die beiden Tangenten schneiden sich in einem Punkt $S.$
Berechne den Abstand des Punktes $S$ vom Ursprung.

(2 VP)

Aufgabe 2

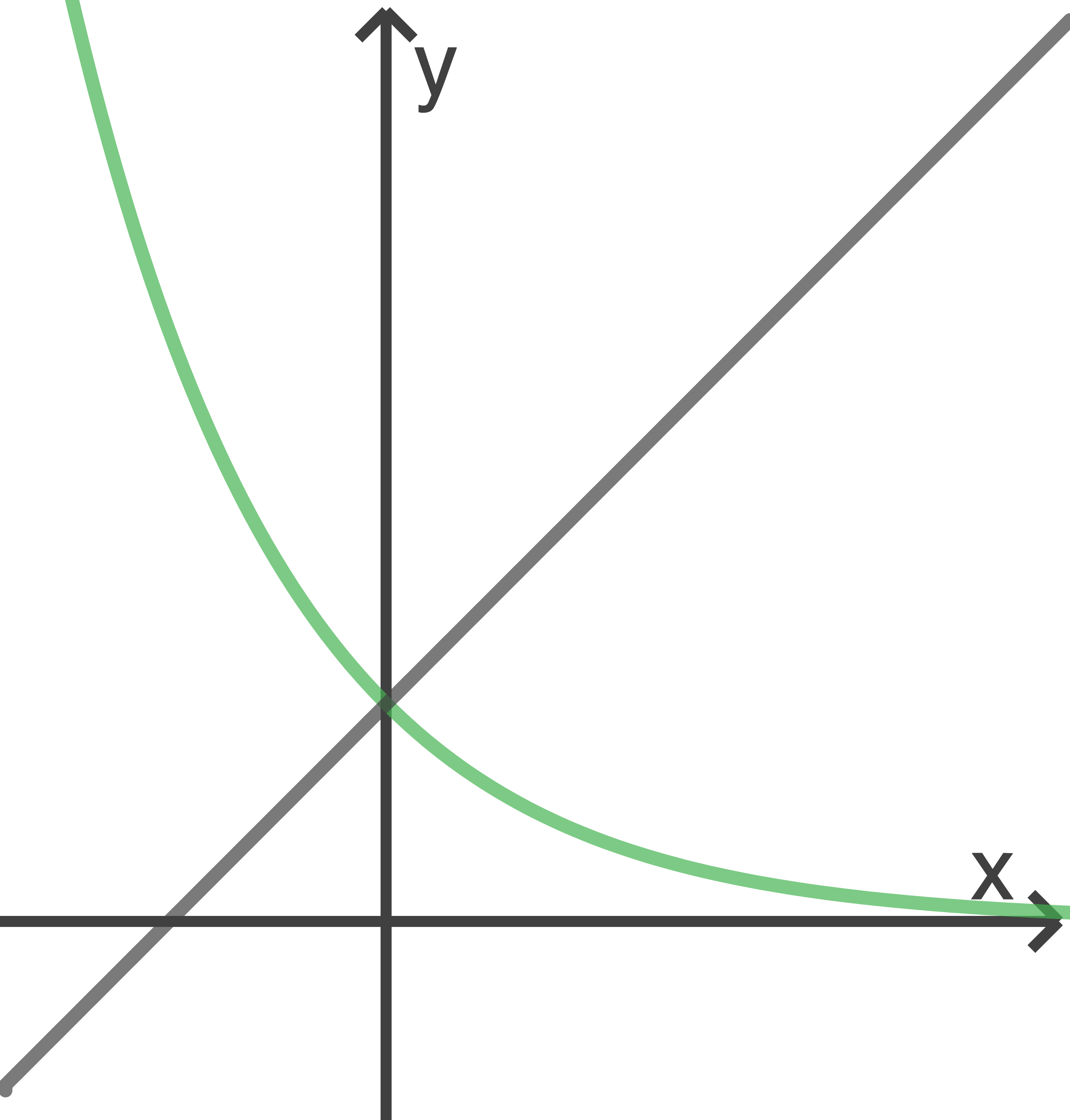
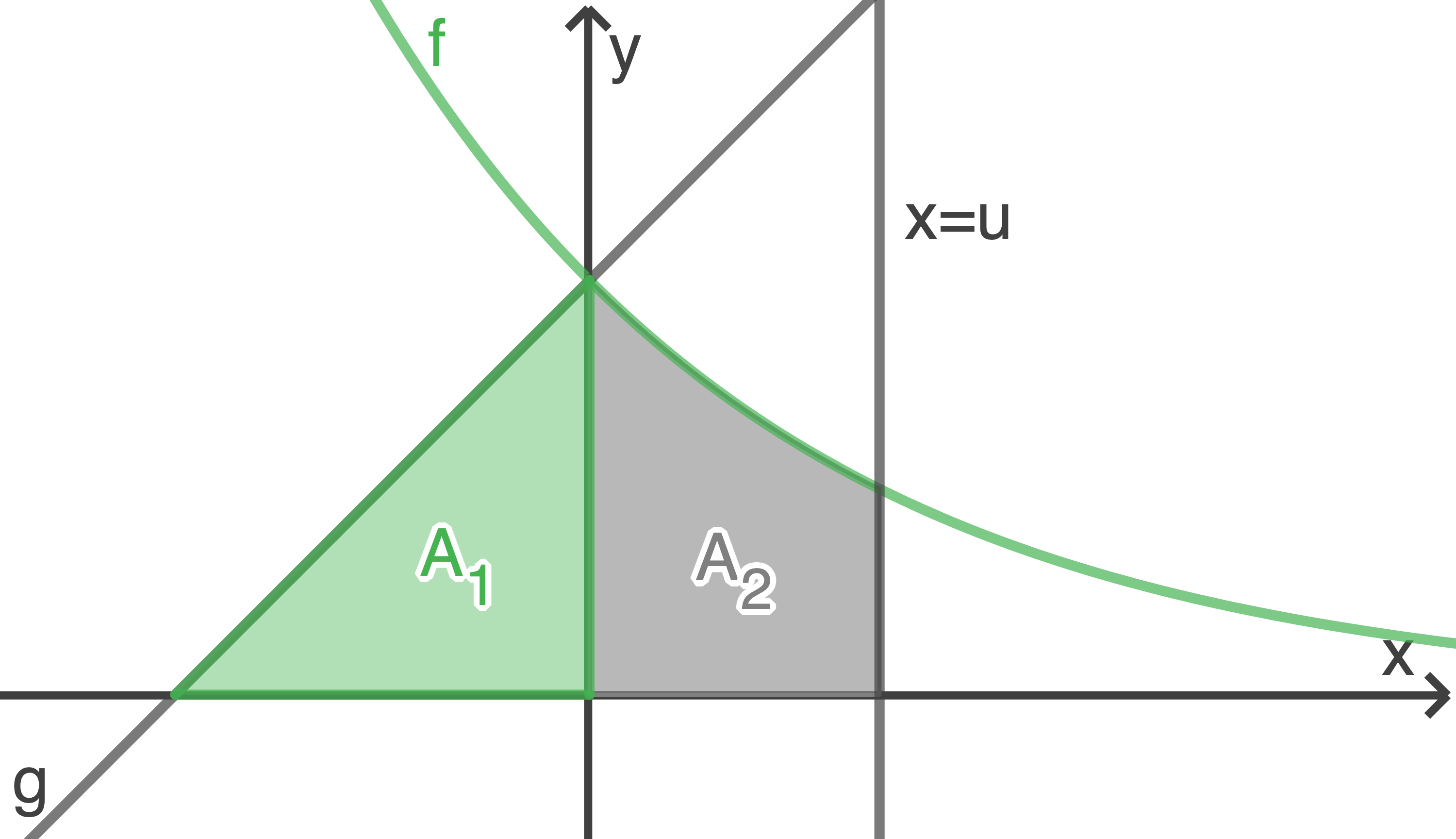
Die Abbildung zeigt die Graphen der Funktionen $f$ und $g$ mit $f(x)= \mathrm e^{-x}$ und $g(x)=x+1$ , deren Schnittpunkt auf der $y$ -Achse liegt.

Die Graphen begrenzen mit der $x$ -Achse und der Geraden $x=u$ $(u \gt 0)$ eine Fläche. Diese Fläche wird von der $y$ -Achse in zwei inhaltsgleiche Teilflächen geteilt.
Berechne den Wert von $u.$

(2,5 VP)

Grafik eines Koordinatensystems mit einer grünen Kurve und den Achsen x und y.

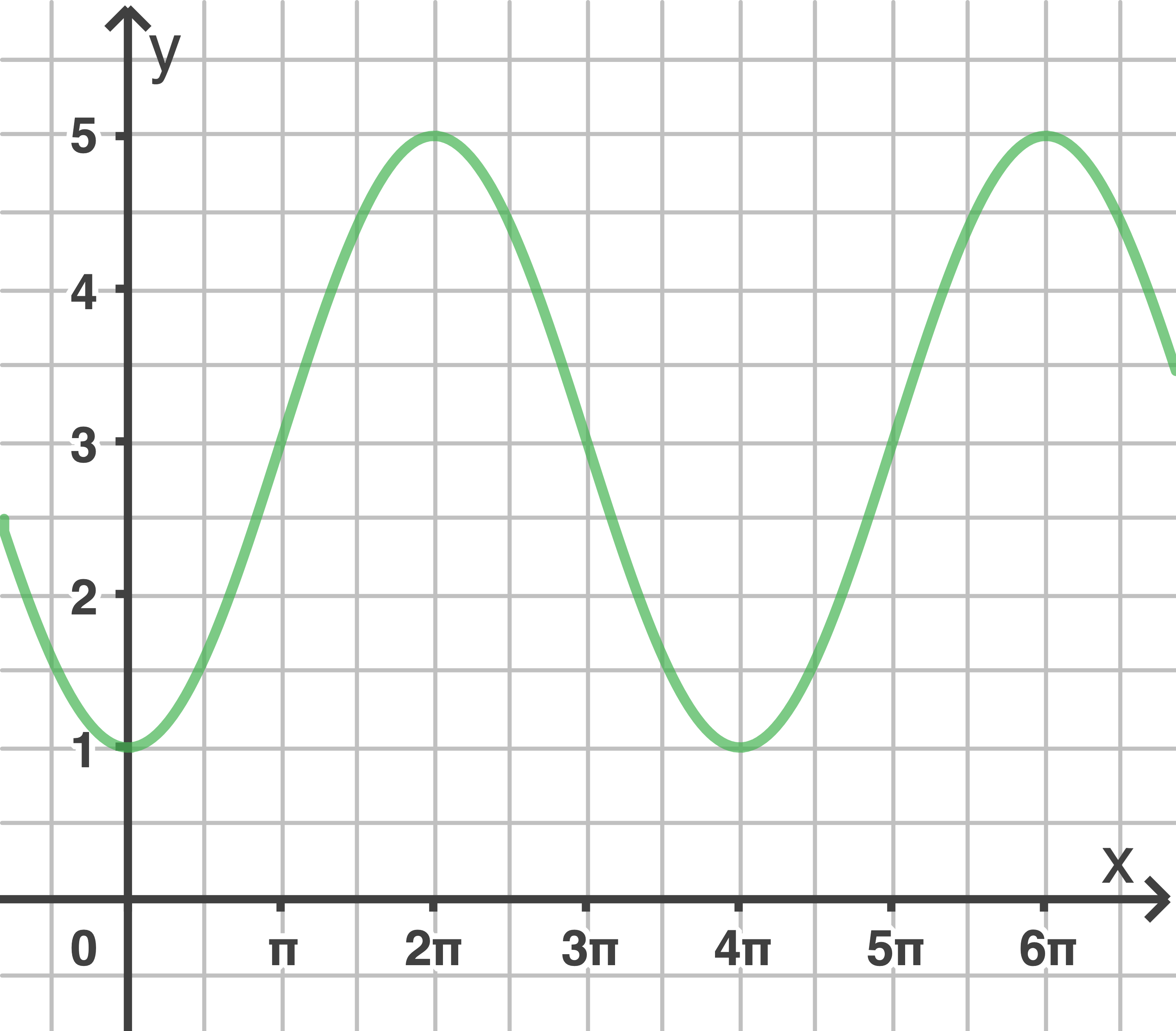
Aufgabe 3

Die Abbildung zeigt den Graphen einer trigonometrischen Funktion.
Bestimme einen möglichen Funktionsterm.

(2,5 VP)

Graph einer sinusförmigen Funktion auf einem Koordinatensystem mit Achsenbeschriftung.

Aufgabe 4

Die Abbildung zeigt den Graphen der Funktion $f.$

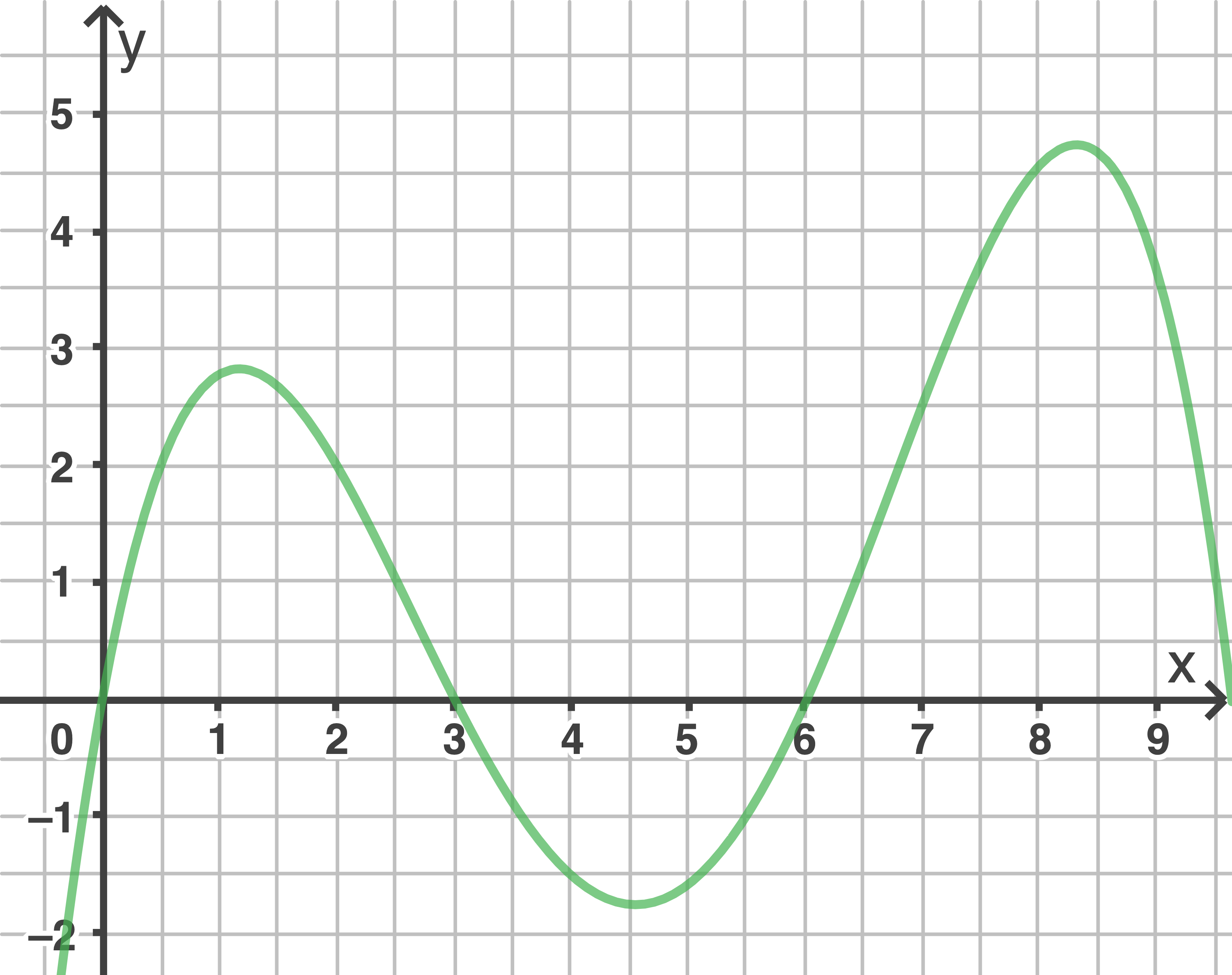
Graph einer Funktion im kartesischen Koordinatensystem mit grüner Kurve.

Begründe, dass die Ableitungsfunktion $\(f$ im Intervall $[5 ;8]$ nicht monoton ist.

(1 VP)

Bestimme die Anzahl der Nullstellen der Funktion $I_2$ mit

$I_2(x)=\displaystyle\int_{2}^{x}f(t)\;\mathrm dt, \; 2 \leq x \leq 9.$

(1,5 VP)

Aufgabe 5

Gegeben sind die Punkte $A(6 \mid 4 \mid -1)$ und $B(0 \mid -5 \mid 2)$ sowie die Ebene $E: 2x_1 -2x_2+x_3 =6.$

Die Gerade durch $A$ und $B$ schneidet $E$ im Punkt $S.$
Bestimme die Koordinaten von $S.$

(1,5 VP)

Untersuche, ob der Punkt $S$ auf der Strecke $AB$ liegt.

(1 VP)

Aufgabe 6

Gegeben ist die Ebene $E: 3x_2-4x_3 =2.$

Beschreibe die besondere Lage von $E$ im Koordinatensystem.

(0,5 VP)

Die Ebene $F$ ist orthogonal zu $E$ und hat zur $x_1-$ Achse den Abstand 2.
Bestimme eine mögliche Koordinatengleichung von $F.$

(2 VP)

Aufgabe 7

Ein Verein erhält eine Lieferung gebrauchter Computer und Bildschirme. Von den 10 Computern und 15 Bildschirmen funktionieren jeweils 3 Geräte nicht. Jemand wählt zufällig einen Computer und einen Bildschirm aus.

Berechne die Wahrscheinlichkeit dafür, dass beide ausgewählten Geräte funktionieren.

(1 VP)

Nach Inbetriebnahme der zwei ausgewählten Geräte stellt sich heraus, dass beide Geräte funktionieren. Anschließend wählt jemand aus den übrigen Geräten der Lieferung zwei Computer aus. Berechne die Wahrscheinlichkeit dafür, dass mindestens einer der beiden zuletzt ausgewählten Computer funktioniert.

(1,5 VP)

Aufgabe 8

Ein idealer Würfel wird 20-mal geworfen. Betrachtet wird die Anzahl der gewürfelten Sechsen.
Gegeben sind drei Terme:

$\text{I}: \left( \dfrac{1}{6} \right)^{11}\cdot \left( \dfrac{5}{6} \right)^{9}$

$\text{II}: \; \pmatrix{20\\11} \cdot \left( \dfrac{1}{6} \right)^{11} \cdot \left( \dfrac{5}{6} \right)^{9}$

$\text{III}: \; 1- \pmatrix{20\\9} \cdot \left(\dfrac{5}{6} \right)^9 \cdot \left(\dfrac{1}{6} \right)^{11}$

Gib an, mit welchem der drei Terme die Wahrscheinlichkeit des Ereignisses "Es wird genau 11-mal eine Sechs gewürfelt.“ berechnet werden kann.

(0,5 VP)

Formuliere für jeden der beiden verbleibenden Terme ein Ereignis im Sachzusammenhang, dessen Wahrscheinlichkeit mit dem jeweiligen Term berechnet werden kann.

(2 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

$\(f$

Mit a) folgt für die Tangente an $G_f$ an der Stelle $x=0:$

$t_1: \, y= 4x$

Da es sich bei $G_f$ um eine Parabel handelt und $G_f$ somit symmetrisch ist, muss die Schnittstelle der beiden Tangenten mittig zwischen den beiden Schnittstellen mit der $x$ -Achse liegen.
Für die Schnittstellen von $f$ mit der $x$ -Achse gilt:

$\begin{array}[t]{rll} f(x) &=& 0 \\[5pt] 4x-x^2 &=& 0 \\[5pt] x\cdot(4-x) &=& 0 \\[5pt] x_1 &=& 0 \\[5pt] x_2 &=& 4 \end{array}$

Die Schnittstelle der beiden Tangenten muss daher $x_S = 2$ sein.
Einsetzen in die Tangentengleichung liefert:

$t_{2}= 4 \cdot 2 =8$

Die Koordinaten des Schnittpunkts lauten also $S(2 \mid 8).$

Der Abstand zum Ursprung beträgt $\sqrt{2^2 +8^2} = \sqrt{68}\,\text{[LE]}.$

Lösung 2

Für die Schnittstelle von $g$ mit der $x$ -Achse gilt:

$0 = x+1$

$-1=x$

Der $y$ -Achsenabschnitt beträgt ebenfalls $1.$

Diagramm mit einer Kurve, Achsen und zwei farblich hervorgehobenen Flächen A1 und A2.

Es folgt also:

$A_1= \dfrac{1}{2} \cdot 1 \cdot 1 = \dfrac{1}{2}$

$A_2= \displaystyle\int_{0}^{u} \mathrm{e}^{-x}\;\mathrm dx = -\mathrm{e}^{-u} +1$

Gleichsetzen von $A_1$ und $A_2$ ergibt:

$\begin{array}[t]{rll} \dfrac{1}{2}&=&-\mathrm{e}^{-u} +1 &\quad \scriptsize \mid\;-1 \\[5pt] -\dfrac{1}{2}&=&-\mathrm{e}^{-u}&\quad \scriptsize \mid\; \cdot (-1) \\[5pt] \dfrac{1}{2}&=& \mathrm{e}^{-u}&\quad \scriptsize \mid\; \ln() \\[5pt] \ln \left(\dfrac{1}{2} \right)&=& -u &\quad \scriptsize \mid\; \cdot (-1) \\[5pt] -\ln \left(\dfrac{1}{2} \right)&=& u \\[5pt] \end{array}$

Lösung 3

Die allgemeine Funktionsgleichung einer Kosinus-Funktion lautet beispielsweise $f(x)= a \cdot \cos(b\cdot (x-c))+d.$ Aus der Abbildung lässt sich $d=3$ , $a=-2$ und $c=0$ ablesen.
Die Periode ergibt sich mit $p=4\pi$ und $b=\dfrac{2 \pi}{p}=\dfrac{1}{2}.$

Folglich lautet die Funktionsgleichung $f(x)= -2\cdot \cos\left( \dfrac{1}{2} x \right) +3.$

Lösung 4

Im Intervall $[5;8]$ besitzt die Funktion $f$ eine Wendestelle, weshalb $\(f$ dort eine Extremstelle hat und nicht monoton ist.

Eine Nullstelle der Funktion ist $x_1=2.$
Anhand des Verlaufs des Graphen können die Teilflächen, die der Graph von $f$ mit der $x$ -Achse einschließt, miteinander verglichen werden. Es gilt: $I_2(3)\gt 0$ , $I_2(6)\lt 0$ und $I_2(9)\gt 0.$ Deshalb muss zwischen diesen Stellen je eine Nullstelle von $I_2$ sein. Im Intervall $[2;9]$ sind insgesamt drei Nullstellen.

Lösung 5

Aufstellen der Geradengleichung:
$g: \overrightarrow{x} =\overrightarrow{OA} + t \cdot \overrightarrow{AB}\,$ $= \pmatrix{6\\4\\-1} + t\cdot \pmatrix{-6\\-9\\3}$

Aus der Geradengleichung folgt $x_1= 6-6t$ , $x_2 = 4-9t$ und $x_3 =-1+3t.$ Eingesetzt in die Ebenengleichung ergibt sich $t.$

Einsetzen anzeigen

$t=-\dfrac{1}{3}$

$t$ eingesetzt in $g$ ergibt $S(4 \mid 1 \mid 0).$

Ja, $S$ liegt auf der Strecke $\overline{AB},$ da er der Schnittpunkt der Geraden durch $A$ und $B$ mit der Ebene $E$ ist und für den zugehörigen Wert des Geradenparameters $0 \leq t=\frac{1}{3} \leq 1$ gilt.

Lösung 6

Die Ebene $E$ liegt parallel zur $x_1$ -Achse.

Da die Ebene $F$ orthogonal zu $E$ und parallel zur $x_1$ -Achse ist, muss das Skalarprodukt der Normalenvektoren der beiden Ebenen, sowie des Normalenvektors von $F$ und dem Richtungsvektor der $x_1$ -Achse Null ergeben.

$\overrightarrow{n_F}\circ \pmatrix{0\\3\\-4} =0$ und $\overrightarrow{n_F} \circ \pmatrix{1\\0\\0} =0$

Mit $\overrightarrow{n_F}= \pmatrix{0\\4\\3}$ ergibt sich die Ebenengleichung zu $F: 4x_2+3x_3 =d$

Damit $F$ den Abstand $2$ zur $x_1$ -Achse hat, genügt es einen Punkt der $x_1$ -Achse zu betrachten. Hat dieser den richtigen Abstand zu $F,$ so gilt dies aufgrund der Parallelität für die gesamte $x_1$ -Achse. Ein möglicher Punkt ist beispielsweise der Koordinatenursprung $O(0\mid 0\mid 0).$ Mit der Hesseschen Normalform folgt:

$\begin{array}[t]{rll} d(F,O) &=& 2 \\[5pt] \dfrac{\left|4\cdot 0+3\cdot 0 -d \right|}{\sqrt{0^2+ 4^2+3^2}} &=& 2 \\[5pt] \dfrac{\left| -d \right|}{5} &=& 2&\quad \scriptsize \mid\; \cdot 5 \\[5pt] \left| -d \right| &=& 10 \\[5pt] \end{array}$

Es kann also $d=10$ oder $d=-10$ gewählt werden. Eine Gleichung der Ebene $F$ lautet also:

$F:\, 4x_2+3x_3 = 10$

Lösung 7

Die Wahrscheinlichkeit dafür, dass beide ausgewählten Geräte funktionieren, ergibt sich mit der Pfadmultiplikationsregel zu:

$p= \dfrac{7}{10}\cdot \dfrac{12}{15}= \dfrac{14}{25}.$

Die Wahrscheinlichkeit, dass mindestens eines der beiden Geräte funktioniert ergibt sich mit dem Gegenereignis und der Pfadmultiplikationsregel zu:

$1-\dfrac{3}{9} \cdot \dfrac{2}{8}= \dfrac{11}{12}.$

Lösung 8

Mit Term $\text{II}$ wird die Wahrscheinlichkeit des Ereignisses „es wird genau 11-mal eine Sechs gewürfelt" berechnet.

Ein geeignetes Ereignis für Term $\text{I}$ ist: Bei den ersten 11 Würfen wird jedes Mal eine Sechs gewürfelt, danach wird keine Sechs mehr gewürfelt.

Ein geeignetes Ereignis für Term $\text{III}$ ist: Es wird nicht genau 11-mal eine Sechs gewürfelt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?