Wahlteil B2
Aufgabe B2.1
An einer rechteckigen Platte mit den Eckpunkten  ,
,  ,
,  und
und  ist im Punkt
ist im Punkt  ein
ein  langer Stab befestigt, der in positive
langer Stab befestigt, der in positive  -Richtung zeigt.
-Richtung zeigt.
Eine punktförmige Lichtquelle befindet sich zunächst im Punkt (Koordinatenangaben in
(Koordinatenangaben in  ).
).
Eine punktförmige Lichtquelle befindet sich zunächst im Punkt
a)
Bestimme eine Koordinatengleichung der Ebene  , in der die Platte liegt.
Stelle die Platte, den Stab und die Lichtquelle in einem Koordinatensystem dar.
Berechne den Winkel zwischen dem Stab und der Platte.
, in der die Platte liegt.
Stelle die Platte, den Stab und die Lichtquelle in einem Koordinatensystem dar.
Berechne den Winkel zwischen dem Stab und der Platte.
(Teilergebnis: )
)
(Teilergebnis:
(3 VP)
b)
Der Stab wirft einen Schatten auf die Platte.
Bestimme den Schattenpunkt des oberen Endes des Stabes.
Begründe, dass der Schatten vollständig auf der Platte liegt.
(3 VP)
c)
Die Lichtquelle bewegt sich von  aus auf einer zur
aus auf einer zur  -Ebene parallelen Kreisbahn, deren Mittelpunkt das obere Ende des Stabes ist. Dabei kollidiert die Lichtquelle mit der Platte.
Berechne die Koordinaten der beiden möglichen Kollisionspunkte.
-Ebene parallelen Kreisbahn, deren Mittelpunkt das obere Ende des Stabes ist. Dabei kollidiert die Lichtquelle mit der Platte.
Berechne die Koordinaten der beiden möglichen Kollisionspunkte.
(3 VP)
Aufgabe B2.2
Bei der Produktion von Bleistiften beträgt der Anteil fehlerhafter Stifte erfahrungsgemäß 
a)
Ein Qualitätsprüfer entnimmt der Produktion zufällig  Bleistifte.
Bleistifte.
Die Zufallsvariable beschreibt die Anzahl der fehlerhaften Stifte in dieser Stichprobe.
Berechne
beschreibt die Anzahl der fehlerhaften Stifte in dieser Stichprobe.
Berechne  .
Mit welcher Wahrscheinlichkeit weicht der Wert von
.
Mit welcher Wahrscheinlichkeit weicht der Wert von  um weniger als
um weniger als  vom Erfahrungswert von
vom Erfahrungswert von  ab?
ab?
Die Zufallsvariable
(3 VP)
b)
Der Betrieb erwirbt eine neue Maschine, von der behauptet wird, dass höchstens  der von ihr produzierten Bleistifte fehlerhaft sind. Diese Hypothese
der von ihr produzierten Bleistifte fehlerhaft sind. Diese Hypothese  soll mithilfe eines Tests an
soll mithilfe eines Tests an  zufällig ausgewählten Stiften überprüft werden.
Bei welchen Anzahlen fehlerhafter Stifte entscheidet man sich gegen die Hypothese, wenn die Irrtumswahrscheinlichkeit maximal
zufällig ausgewählten Stiften überprüft werden.
Bei welchen Anzahlen fehlerhafter Stifte entscheidet man sich gegen die Hypothese, wenn die Irrtumswahrscheinlichkeit maximal  betragen soll?
betragen soll?
(3 VP)
Aufgabe B2.1
a)  Bestimmen der Koordinatengleichung der Ebene
Bestimmen der Koordinatengleichung der Ebene  , in der die Platte liegt
Der Aufgabenstellung kannst du entnehmen, dass die rechteckige Platte die folgenden Eckpunkte besitzt:
, in der die Platte liegt
Der Aufgabenstellung kannst du entnehmen, dass die rechteckige Platte die folgenden Eckpunkte besitzt:
 zu bestimmen, in welcher die rechteckige Platte liegt. Die Ebenengleichung in Koordinatenform einer Ebene baut sich dabei wie folgt auf:
zu bestimmen, in welcher die rechteckige Platte liegt. Die Ebenengleichung in Koordinatenform einer Ebene baut sich dabei wie folgt auf:
 mit:
mit:
 bestimmen, so bestimmst du zunächst den Normalenvektor
bestimmen, so bestimmst du zunächst den Normalenvektor  über das Kreuz- bzw. Vektorprodukt. Verwende dazu die Koordinaten der Eckpunkte der rechteckigen Platte.
über das Kreuz- bzw. Vektorprodukt. Verwende dazu die Koordinaten der Eckpunkte der rechteckigen Platte.
 über das Kreuzprodukt
Willst du den Normalenvektor
über das Kreuzprodukt
Willst du den Normalenvektor  der Ebene
der Ebene  bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene
bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene  aufspannen. Gehe hier beispielsweise von Punkte
aufspannen. Gehe hier beispielsweise von Punkte  aus. Punkt
aus. Punkt  ist über eine Kante mit Punkt
ist über eine Kante mit Punkt  und
und  verbunden:
verbunden:
![\(\begin{array}[t]{rll}
\overrightarrow{AB} &=&\overrightarrow{OB} - \overrightarrow{OA} & \\[5pt]
&=& \begin{pmatrix}0 \\ 6 \\ 0\end{pmatrix} - \begin{pmatrix}10\\6\\0\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}0 &-& 10 \\ 6 &-& 6 \\ 0 &-& 0\end{pmatrix} & \\[5pt]
&=& \begin{pmatrix}-10 \\ 0 \\ 0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/dd61f4afb9ae8bcb124aaef1a5699fea71f158f86c1ca3e573ac3ed772b1c8be?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{AD}&=& \overrightarrow{OD} - \overrightarrow{OA}& \\[5pt]
&=& \begin{pmatrix}10 \\ 0 \\ 3\end{pmatrix} - \begin{pmatrix}10\\6\\0\end{pmatrix} & \\[5pt]
&=& \begin{pmatrix}10 &-& 10 \\ 0 &-& 6 \\ 3 &-& 0\end{pmatrix}& \\[5pt]
&=&\begin{pmatrix}0 \\ -6 \\ 3\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/7e0c555f2176daacf7a5c908a3d82bff1adabf083fd7fc47c8b0024749706870?color=5a5a5a) Berechne nun wie folgt das Kreuzprodukt der Vektoren
Berechne nun wie folgt das Kreuzprodukt der Vektoren  und
und  , um den Normalenvektor
, um den Normalenvektor  zu bestimmen:
Da beim Normalenvektor
zu bestimmen:
Da beim Normalenvektor  nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
 2. Schritt: Bestimmen der Koordinatengleichung über eine Punktprobe
Setzt du nun den Normalenvektor
2. Schritt: Bestimmen der Koordinatengleichung über eine Punktprobe
Setzt du nun den Normalenvektor  in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
Die Konstante
in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
Die Konstante  bestimmst du hier nun, indem du beispielsweise die Koordinaten von
bestimmst du hier nun, indem du beispielsweise die Koordinaten von  mit
mit  für
für  ,
,  und
und  einsetzt und die Gleichung nach
einsetzt und die Gleichung nach  löst:
löst:
 Eine Koordinatengleichung der Ebene
Eine Koordinatengleichung der Ebene  lautet also:
lautet also:
 .
.
 Darstellen des Sachverhaltes in einem Koordinatensystem
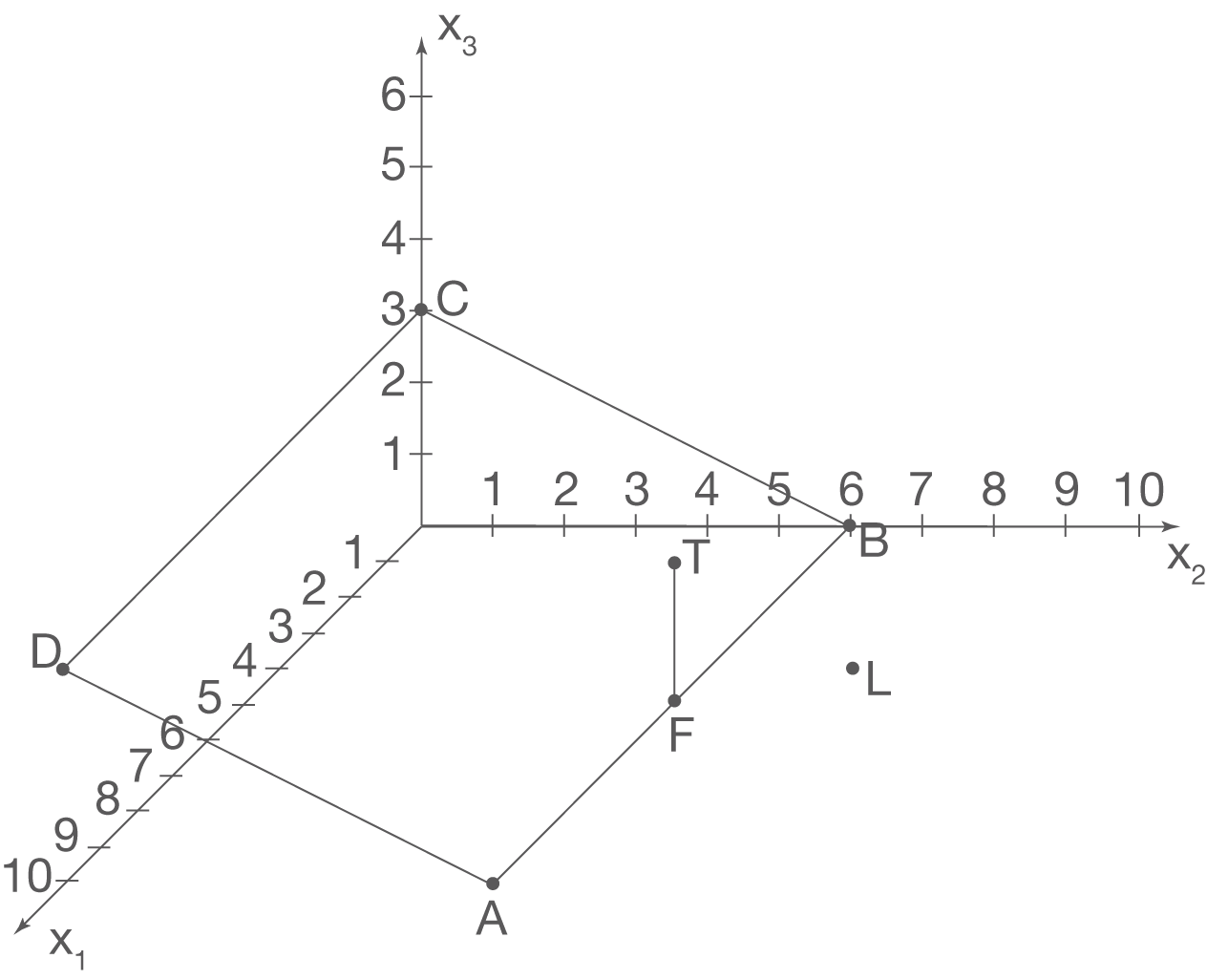
Hier sollst du nun die Platte, den Stab und die Lichtquelle in einem Koordinatensystem darstellen. Orientiere dich beim Zeichnen der Achsen an den Koordinaten der einzuzeichnenden Punkte und denke daran, dass alle Koordinatenangaben in deinem Koordinatensystem in m sind. Zeichne zunächst die Platte mit:
Darstellen des Sachverhaltes in einem Koordinatensystem
Hier sollst du nun die Platte, den Stab und die Lichtquelle in einem Koordinatensystem darstellen. Orientiere dich beim Zeichnen der Achsen an den Koordinaten der einzuzeichnenden Punkte und denke daran, dass alle Koordinatenangaben in deinem Koordinatensystem in m sind. Zeichne zunächst die Platte mit:
 ein und von diesem dann einen 2 m langen Stab. Zuletzt zeichnest du die Lichtquelle
ein und von diesem dann einen 2 m langen Stab. Zuletzt zeichnest du die Lichtquelle  bei
bei  ein.
ein.
Deine Zeichnung sollte hier so aussehen:
 Bestimmen des Winkels zwischen Stab und Platte
Nun sollst du den Winkel
Bestimmen des Winkels zwischen Stab und Platte
Nun sollst du den Winkel  zwischen dem Stab bei
zwischen dem Stab bei  und der Platte
und der Platte  bestimmen. Da der Stab durch einen Vektor
bestimmen. Da der Stab durch einen Vektor  (siehe oben) und die Platte
(siehe oben) und die Platte  durch eine Ebene repräsentiert werden können, gilt es hier einen Winkel zwischen einer Ebene und einem Vektor zu berechnen.
durch eine Ebene repräsentiert werden können, gilt es hier einen Winkel zwischen einer Ebene und einem Vektor zu berechnen.
Für die Berechnung eines Winkels zwischen einem Vektor und einer Ebene gilt dabei folgendes: mit:
mit:
 der den Stab repräsentiert und bestimme dann mit dem Normalenvektor
der den Stab repräsentiert und bestimme dann mit dem Normalenvektor  der Ebene
der Ebene  den hier gesuchten Winkel.
den hier gesuchten Winkel.
Da der Stab 2 m lang ist und in positive -Richtung zeigt, ergibt sich der Vektor
-Richtung zeigt, ergibt sich der Vektor  hier wie folgt:
hier wie folgt:
 Setze nun
Setze nun  und
und  in den Zusammenhang von oben ein, um den hier gesuchten Winkel
in den Zusammenhang von oben ein, um den hier gesuchten Winkel  zu bestimmen:
Der Winkel zwischen Stab und Platte beträgt also ungefähr 63,4°.
zu bestimmen:
Der Winkel zwischen Stab und Platte beträgt also ungefähr 63,4°.
;
;
und
.
,
und
: Einträge des Normalenvektors
der Ebene
: Über Punktprobe zu bestimmende Konstante
Hast du den Normalenvektor  der Ebene
der Ebene  bestimmt, so bestimmst du über eine Punktprobe die Konstante
bestimmt, so bestimmst du über eine Punktprobe die Konstante  . Verwende dazu die Koordinaten von Punkt
. Verwende dazu die Koordinaten von Punkt  ,
,  ,
,  oder
oder  .
.
1. Schritt: Bestimmen des Normalenvektors ;
;
und
.
Deine Zeichnung sollte hier so aussehen:

Für die Berechnung eines Winkels zwischen einem Vektor und einer Ebene gilt dabei folgendes:
: Betrachteter Vektor;
: Normalenvektor der betrachteten Ebene.
Da der Stab 2 m lang ist und in positive
b)  Berechnen des Schattenpunktes des oberen Endes des Stabes
Der Aufgabenstellung kannst du entnehmen, dass sich im Punkt
Berechnen des Schattenpunktes des oberen Endes des Stabes
Der Aufgabenstellung kannst du entnehmen, dass sich im Punkt  eine punktförmige Lichtquelle befindet. Weiterhin weißt du, dass der Stab einen Schatten auf die Platte wirft. Deine Aufgabe ist es dabei, die Koordinaten des Schattenpunktes
eine punktförmige Lichtquelle befindet. Weiterhin weißt du, dass der Stab einen Schatten auf die Platte wirft. Deine Aufgabe ist es dabei, die Koordinaten des Schattenpunktes  des oberen Endes des Stabes, welcher dieser auf die Platte wirft, zu bestimmen.
des oberen Endes des Stabes, welcher dieser auf die Platte wirft, zu bestimmen.
Aus dem vorhergegangenen Aufgabenteil weißt du, dass das obere Ende des Stabes die Koordinaten besitzt. Nun werden von Punkt
besitzt. Nun werden von Punkt  aus Lichtstrahlen in Richtung des Stabes geworfen. Das heißt, die „Richtung des Schattens“ des oberen Endes des Stabes wird durch den Vektor
aus Lichtstrahlen in Richtung des Stabes geworfen. Das heißt, die „Richtung des Schattens“ des oberen Endes des Stabes wird durch den Vektor  bestimmt. Willst du nun ausgehend von dem Wissen über diesen Vektor den Schattenpunkt
bestimmt. Willst du nun ausgehend von dem Wissen über diesen Vektor den Schattenpunkt  bestimmen, so gehst du hier so vor:
bestimmen, so gehst du hier so vor:
 Soll Gerade
Soll Gerade  die Richtung des Lichtes, ausgehend von Punkt
die Richtung des Lichtes, ausgehend von Punkt  beschreiben, so muss diese den Vektor
beschreiben, so muss diese den Vektor  als Stütz- und den Vektor
als Stütz- und den Vektor  als Richtungsvektor besitzen.
als Richtungsvektor besitzen.
![\(\begin{array}[t]{rll}
\overrightarrow{LT}&=& \overrightarrow{OT} - \overrightarrow{OL} &\\[5pt]
&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} - \begin{pmatrix}8 \\ 10 \\ 2\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}5 &-& 8 \\ 6 &-& 10 \\ 2 &-& 2\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/f3e54cbb98e5f6d6fffc106812b214b8d31052ff9137e515b46b1d151008ec10?color=5a5a5a)
![\(\begin{array}[t]{rll}
l: \quad \overrightarrow{x} &=& \overrightarrow{OT} + t \cdot \overrightarrow{LT}&\\[5pt]
&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} + t \cdot \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/337088f1d403968d343b25119aae02dcd471bfcadbe6db687f9aa73dc4f76d6f?color=5a5a5a) 2. Schritt: Bestimmen des Schattenpunktes
2. Schritt: Bestimmen des Schattenpunktes  Willst du den Schnittpunkt von Ebene
Willst du den Schnittpunkt von Ebene  und Gerade
und Gerade  bestimmen, so formulierst du zunächst Gerade
bestimmen, so formulierst du zunächst Gerade  als einen einzelnen Vektor. Anschließend setzt du die Einträge dieses Vektors in die Koordinatengleichung von
als einen einzelnen Vektor. Anschließend setzt du die Einträge dieses Vektors in die Koordinatengleichung von  ein und berechnest den zu
ein und berechnest den zu  zugehörigen Parameterwert von
zugehörigen Parameterwert von  .
.
![\(\begin{array}[t]{rll}
l: \quad \overrightarrow{x_l}&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} + t \cdot \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}5 - 3 \cdot t \\ 6 - 4 \cdot t \\ 2\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/db7cda6f53ce90404abadb996d5412cc675cece47a3d654d73ab3b5c8d393c78?color=5a5a5a) Ein Einsetzen von
Ein Einsetzen von  in die Koordinatengleichung von
in die Koordinatengleichung von  , für
, für  ,
,  und
und  ergibt:
ergibt:
 Setze nun
Setze nun  in die Geradengleichung von
in die Geradengleichung von  ein, um die Koordinaten von Schattenpunkt
ein, um die Koordinaten von Schattenpunkt  zu bestimmen:
zu bestimmen:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} + 1 \cdot \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}5 &-& 3 \\ 6 &-& 4 \\ 2 &+& 0\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}2 \\ 2 \\ 2\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/3a7b22251d72978d9be8afdecc59a72818009ee197e6d98075b10eaa27cbdf44?color=5a5a5a) Der Schattenpunkt des oberen Endes des Stabes hat die Koordinaten:
Der Schattenpunkt des oberen Endes des Stabes hat die Koordinaten:  .
.
 Begründen, dass der Schatten vollständig auf der Platte liegt
Nun sollst du begründen, dass der Schatten, den der Stab wirft, sich vollständig auf der Platte befindet. Von oben weißt du, dass der Schattenpunkt, welcher vom oberen Ende des Stabes geworfen wird, die Koordinaten
Begründen, dass der Schatten vollständig auf der Platte liegt
Nun sollst du begründen, dass der Schatten, den der Stab wirft, sich vollständig auf der Platte befindet. Von oben weißt du, dass der Schattenpunkt, welcher vom oberen Ende des Stabes geworfen wird, die Koordinaten  besitzt.
besitzt.
Willst du hier begründen, dass der Schatten, welcher vom Stab geworfen wird, sich vollständig auf der Platte befindet, so musst du hier folgendes tun: mit den Koordinaten der Eckpunkte
mit den Koordinaten der Eckpunkte  ,
,  ,
,  und
und  , so kannst du hier folgendes feststellen:
, so kannst du hier folgendes feststellen:
 liegt also offensichtlich auf der Platte. Da auch der Anfangspunkt
liegt also offensichtlich auf der Platte. Da auch der Anfangspunkt  mit
mit  des Stabes sich auf der Platte befindet, muss sich der Schatten zwischen
des Stabes sich auf der Platte befindet, muss sich der Schatten zwischen  und
und  ebenfalls auf der Platte befinden. Dies lässt sich auch wie folgt an der Zeichnung aus a veranschaulichen:
ebenfalls auf der Platte befinden. Dies lässt sich auch wie folgt an der Zeichnung aus a veranschaulichen:
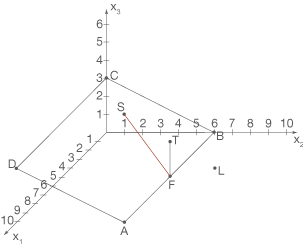 Der Schatten wurde hier in rot eingezeichnet.
Der Schatten wurde hier in rot eingezeichnet.
Aus dem vorhergegangenen Aufgabenteil weißt du, dass das obere Ende des Stabes die Koordinaten
- Formuliere eine Gerade
, die die Richtung des Lichtes ausgehend vom Punkt
beschreibt.
- Schneide die Gerade mit der Ebene
, die die Platte repräsentiert
- Der Schnittpunkt von Gerade
und Ebene
ist dann der gesuchte Schattenpunkt
.
Willst du hier begründen, dass der Schatten, welcher vom Stab geworfen wird, sich vollständig auf der Platte befindet, so musst du hier folgendes tun:
- Vergleiche die Koordinaten von Punkt
mit den Koordinaten der Eckpunkte der Platte.
- Analysiere die Koordinaten von Punkt
nochmals genauer und setze sie in Relation zu den Koordinaten von
.
- Veranschauliche deine Überlegungen an der Skizze aus Aufgabenteil a.
- Der Schattenpunkt
liegt in der Ebene
.
- Die
-Koordinate von
liegt zwischen den
-Koordinaten von
und
.
- Die
-Koordinate von
liegt zwischen den
-Koordinaten von
und
.

c)  Berechnen der Koordinaten der möglichen Kollisionspunkte
Der Aufgabenstellung kannst du nun entnehmen, dass sich die Lichtquelle von
Berechnen der Koordinaten der möglichen Kollisionspunkte
Der Aufgabenstellung kannst du nun entnehmen, dass sich die Lichtquelle von  aus auf einer zur
aus auf einer zur  -Ebene parallelen Kreisbahn bewegt. Der Mittelpunkt dieser Kreisbahn ist dabei Punkt
-Ebene parallelen Kreisbahn bewegt. Der Mittelpunkt dieser Kreisbahn ist dabei Punkt  , also das obere Ende des Stabes. Bewegt sich die Lichtquelle wie eben beschrieben auf der Kreisbahn, so kollidiert diese mit der Platte
, also das obere Ende des Stabes. Bewegt sich die Lichtquelle wie eben beschrieben auf der Kreisbahn, so kollidiert diese mit der Platte  . Deine Aufgabe ist es nun, die Koordinaten dieser möglichen Kollisionspunkte zu berechnen.
. Deine Aufgabe ist es nun, die Koordinaten dieser möglichen Kollisionspunkte zu berechnen.
Willst du hier die möglichen Kollisionspunkte bestimmen, so bestimmst du zunächst die Ebene , auf welcher sich die Lichtquelle bewegt. Beachte dabei, dass diese parallel zur
, auf welcher sich die Lichtquelle bewegt. Beachte dabei, dass diese parallel zur  -Ebene verlaufen muss.
-Ebene verlaufen muss.
Hast du Ebene bestimmt, so schneidest du diese mit der Ebene
bestimmt, so schneidest du diese mit der Ebene  , in welcher sich auch die Platte befindet. Da du hier zwei Ebenen schneidest, ergibt sich als Resultat eine Schnittgerade. Auf dieser Schnittgeraden müssen sich dann die möglichen Kollisionspunkte befinden. Überlege dir folgendes, um diese dann zu bestimmen:
, in welcher sich auch die Platte befindet. Da du hier zwei Ebenen schneidest, ergibt sich als Resultat eine Schnittgerade. Auf dieser Schnittgeraden müssen sich dann die möglichen Kollisionspunkte befinden. Überlege dir folgendes, um diese dann zu bestimmen:
 Wie oben beschrieben, müssen die gesuchten Kollisionspunkte auf der Schnittgeraden liegen, welche sich ergibt, wenn du Ebene
Wie oben beschrieben, müssen die gesuchten Kollisionspunkte auf der Schnittgeraden liegen, welche sich ergibt, wenn du Ebene  und Ebene
und Ebene  schneidest. Da die Kreisbahn parallel zur
schneidest. Da die Kreisbahn parallel zur  -Ebene sein soll, muss die Ebene, in welcher sie sich befindet, ebenfalls parallel zur
-Ebene sein soll, muss die Ebene, in welcher sie sich befindet, ebenfalls parallel zur  -Ebene sein.
-Ebene sein.
Betrachtest du die Koordinaten von und
und  genauer, so kannst du erkennen, dass beide eine
genauer, so kannst du erkennen, dass beide eine  -Koordinate von
-Koordinate von  haben. Da nun Punkt
haben. Da nun Punkt  und Punkt
und Punkt  in der Ebene
in der Ebene  liegen sollen und diese darüber hinaus auch noch parallel zur
liegen sollen und diese darüber hinaus auch noch parallel zur  -Ebene sein soll, lautet eine Koordinatengleichung dieser Ebene:
-Ebene sein soll, lautet eine Koordinatengleichung dieser Ebene:
 .
Willst du nun die Schnittgerade
.
Willst du nun die Schnittgerade  bestimmen, so formulierst du aus den Koordinatengleichungen von
bestimmen, so formulierst du aus den Koordinatengleichungen von  und
und  ein unterbesetztes Gleichungssystem. Führe in diesem Gleichungssystem für
ein unterbesetztes Gleichungssystem. Führe in diesem Gleichungssystem für  einen Parameter ein, um es eindeutig lösen zu können:
Gib nun die Lösungsmenge des LGS an und formuliere aus dieser wie folgt die Gerade
einen Parameter ein, um es eindeutig lösen zu können:
Gib nun die Lösungsmenge des LGS an und formuliere aus dieser wie folgt die Gerade 
![\(\begin{array}[t]{rll}
\mathbb L &=& \left\{\begin{pmatrix}r \\ 2 \\ 2\end{pmatrix}\right\}\;& \\[5pt]
&=& \; \left\{\begin{pmatrix}0 \\ 2 \\ 2\end{pmatrix} + r \cdot \begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix}\right\}
\end{array}\)](https://mathjax.schullv.de/df60e25c675592e8c48180868c03ed9b6380894392ecf844cb99e413ef1ee347?color=5a5a5a) Schnittgerade
Schnittgerade  hat also folgende Gleichung:
hat also folgende Gleichung:
 2. Schritt: Bestimmen der möglichen Kollisionspunkte
Nun weißt du folgende zwei Dinge über die Lage der Kollisionspunkte:
2. Schritt: Bestimmen der möglichen Kollisionspunkte
Nun weißt du folgende zwei Dinge über die Lage der Kollisionspunkte:
 liegen und einen Abstand von 5 zu
liegen und einen Abstand von 5 zu  besitzen. Formuliere dazu auch hier wieder Gerade
besitzen. Formuliere dazu auch hier wieder Gerade  als Vektor um:
als Vektor um:
![\(\begin{array}[t]{rll}
s:\quad \overrightarrow{x_S}&=& \overrightarrow{K_r} & \\[5pt]
&=& \begin{pmatrix}0 \\ 2 \\ 2\end{pmatrix} + r \cdot \begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}r \\ 2 \\ 2\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/140de7c62e96609d1d0a6da987346251034d10419a9c7954e55c1ab45894c72a?color=5a5a5a) Bestimmst du nun den Betrag des Vektors
Bestimmst du nun den Betrag des Vektors  , so hast du den von
, so hast du den von  abhängigen Abstand zwischen Punkt
abhängigen Abstand zwischen Punkt  und den Kollisionspunkten
und den Kollisionspunkten  . Setzt du diesen Abstand gleich 5 so kannst du wie folgt die Koordinaten der möglichen Kollisionspunkte bestimmen:
. Setzt du diesen Abstand gleich 5 so kannst du wie folgt die Koordinaten der möglichen Kollisionspunkte bestimmen:
![\(\begin{array}[t]{rll}
5&=& \left|\overrightarrow{TK_r}\right|& \\[5pt]
&=& \left|\begin{pmatrix}r \\ 2 \\ 2\end{pmatrix} - \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix}\right|& \\[5pt]
&=&\left|\begin{pmatrix}r - 5 \\ -4 \\ 0\end{pmatrix}\right| & \\[5pt]
&=& \sqrt{(r - 5)^2 + (-4)^2 + 0^2}& \\[5pt]
&=& \sqrt{(r - 5)^2 + 16}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7f42e6a17b12dfeee87eeece375ed78ab1b53ac49589f300f2be3dcb08e453ea?color=5a5a5a) Diese Gleichung kannst du nun graphisch mit Hilfe deines GTR lösen. Übertrage die rechte Seite dazu in den Y-Editor, als eine von x-abhängige Gleichung. Die linke Seite der Gleichung überträgst du als eine zur
Diese Gleichung kannst du nun graphisch mit Hilfe deines GTR lösen. Übertrage die rechte Seite dazu in den Y-Editor, als eine von x-abhängige Gleichung. Die linke Seite der Gleichung überträgst du als eine zur  -Achse parallele Gerade in deinen GTR (siehe unten links). Wechsle anschließend in den GRAPH-Modus und bestimme über
-Achse parallele Gerade in deinen GTR (siehe unten links). Wechsle anschließend in den GRAPH-Modus und bestimme über
die Schnittpunkte der beiden Funktionen.
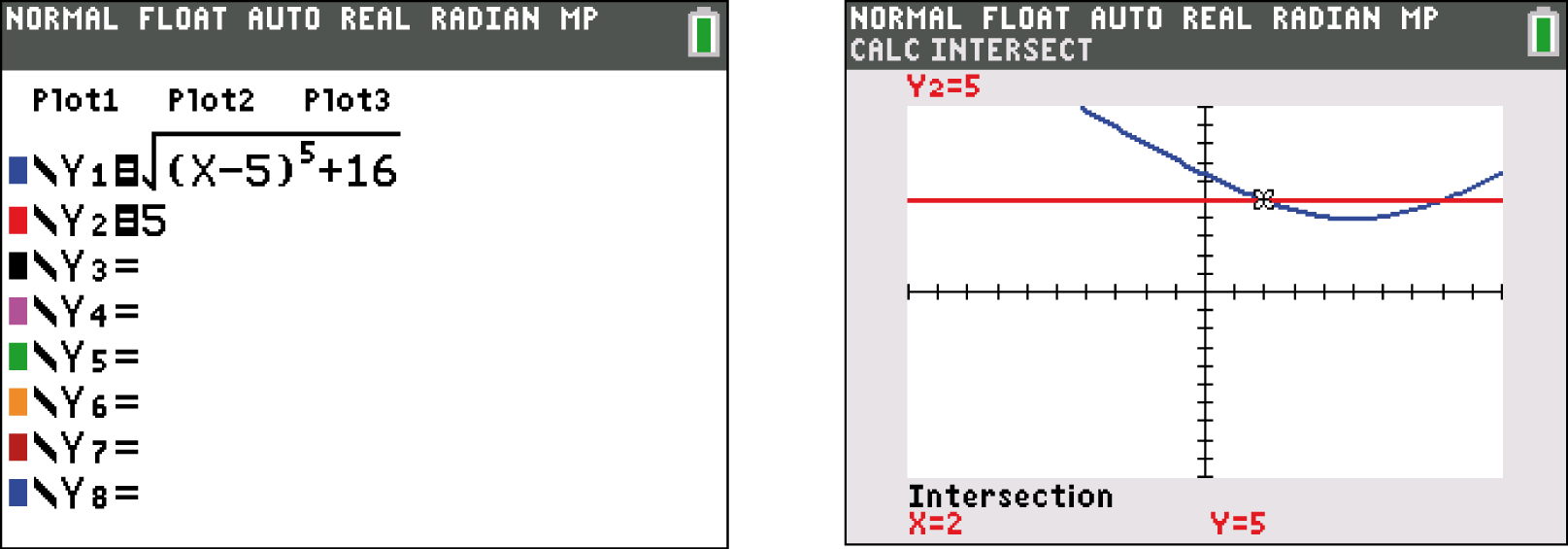 Als Lösung der Gleichung hat sich also ergeben:
Als Lösung der Gleichung hat sich also ergeben:  und
und  . Setze diese nun in die allgemeinen Koordinaten von
. Setze diese nun in die allgemeinen Koordinaten von  ein, so ergeben sich folgende zwei möglich Kollisionspunkte:
ein, so ergeben sich folgende zwei möglich Kollisionspunkte:
Willst du hier die möglichen Kollisionspunkte bestimmen, so bestimmst du zunächst die Ebene
Hast du Ebene
- Die Kollisionspunkte müssen sich auf der Schnittgeraden befinden;
- der Radius der Kreisbahn wird durch den Abstand zwischen
und
bestimmt;
- da es sich beim Punkt
um den Mittelpunkt des Kreises handelt, muss der Abstand zwischen
und den Kollisionspunkten gerade dem Radius entsprechen.
- Verwende beim Berechnen die allgemeinen Koordinaten der Kollisionspunkte, die sich aus der Schnittgeraden ergeben.
Betrachtest du die Koordinaten von
- Sie liegen auf der Gerade
und
- sie besitzen zum Punkt
einen Abstand von 5 m.
|
2ND |

und
.
Lösung B2.2
a)  Berechnen der gesuchten Wahrscheinlichkeit
Der Aufgabenstellung kannst du entnehmen, dass bei der Produktion von Bleistiften erfahrungsgemäß der Anteil der fehlerhaften Stifte bei 5 % liegt. Nun werden der Produktion zur Qualitätsprüfung zufällig 800 Bleistifte entnommen. Die Zufallsvariable
Berechnen der gesuchten Wahrscheinlichkeit
Der Aufgabenstellung kannst du entnehmen, dass bei der Produktion von Bleistiften erfahrungsgemäß der Anteil der fehlerhaften Stifte bei 5 % liegt. Nun werden der Produktion zur Qualitätsprüfung zufällig 800 Bleistifte entnommen. Die Zufallsvariable  beschreibt dabei die Anzahl der fehlerhaften Stifte in der vorliegenden Stichprobe. Deine Aufgabe ist es nun, die Wahrscheinlichkeit
beschreibt dabei die Anzahl der fehlerhaften Stifte in der vorliegenden Stichprobe. Deine Aufgabe ist es nun, die Wahrscheinlichkeit  zu berechnen.
zu berechnen.
Da die Zufallsvariable nur die Ausprägungen
nur die Ausprägungen
 näherungsweise binomialverteilt. Für den Stichprobenumfang gilt
näherungsweise binomialverteilt. Für den Stichprobenumfang gilt  . Die Wahrscheinlichkeit
. Die Wahrscheinlichkeit  für einen fehlerhaften Stift ergibt sich aus dem relativen Anteil der fehlerhaften Stifte in der Produktion. Für
für einen fehlerhaften Stift ergibt sich aus dem relativen Anteil der fehlerhaften Stifte in der Produktion. Für  gilt also:
gilt also:
Willst du die hier gesuchte Wahrscheinlichkeit mit deinem GTR berechnen, so wechselst du zunächst in den Calculator-Modus deines GTR. In diesem wendest du dann den binomCdf-Befehl an, auf welchen du über
zugreifst. Willst du die Wahrscheinlichkeit hier berechnen, so wendest du den binomCdf-Befehl wie in den unten stehenden Schaubildern an.
hier berechnen, so wendest du den binomCdf-Befehl wie in den unten stehenden Schaubildern an.
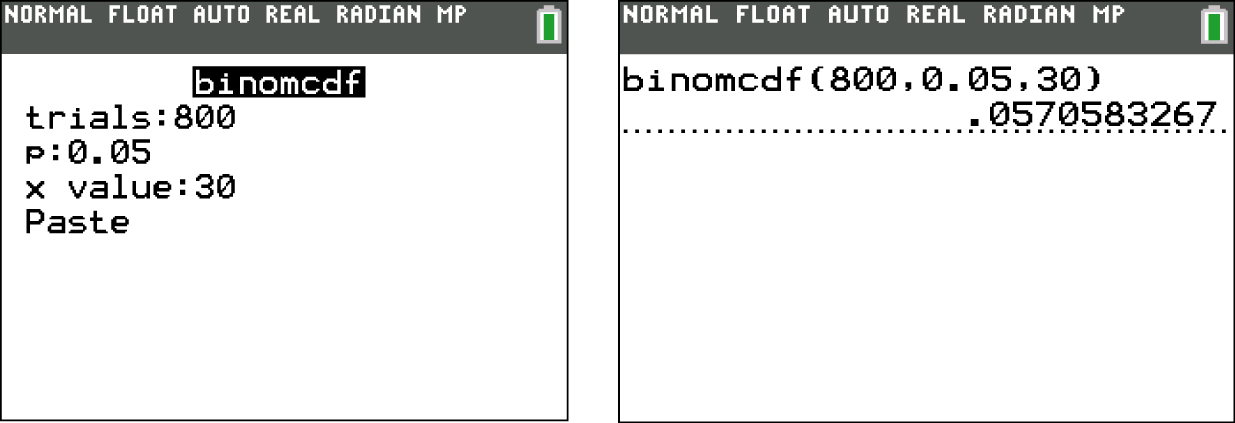 Für die Wahrscheinlichkeit
Für die Wahrscheinlichkeit  gilt also:
gilt also:  .
.
 Wahrscheinlichkeit, für die geg. Abweichung vom Erwartungswert
Hier sollst du nun die Wahrscheinlichkeit dafür bestimmen, dass der Wert von
Wahrscheinlichkeit, für die geg. Abweichung vom Erwartungswert
Hier sollst du nun die Wahrscheinlichkeit dafür bestimmen, dass der Wert von  um weniger als 10 vom Erwartungswert der Zufallsvariable
um weniger als 10 vom Erwartungswert der Zufallsvariable  abweicht. Bestimme dazu zunächst den Erwartungswert der Zufallsvariablen
abweicht. Bestimme dazu zunächst den Erwartungswert der Zufallsvariablen  . Der Erwartungswert einer binomialverteilten Zufallsvariablen ergibt sich dabei wie folgt:
. Der Erwartungswert einer binomialverteilten Zufallsvariablen ergibt sich dabei wie folgt:
 bestimmt, so formulierst du im nächsten Schritt die hier zu berechnende Wahrscheinlichkeit. Beachte dabei das hier eine Abweichung „nach oben“ und „nach unten“ beachtet werden muss. Die hier zu berechnende Wahrscheinlichkeit hat also diese Gestalt:
bestimmt, so formulierst du im nächsten Schritt die hier zu berechnende Wahrscheinlichkeit. Beachte dabei das hier eine Abweichung „nach oben“ und „nach unten“ beachtet werden muss. Die hier zu berechnende Wahrscheinlichkeit hat also diese Gestalt:
 mit:
mit:
 Setze
Setze  und
und  in die Formel für den Erwartungswert
in die Formel für den Erwartungswert  ein, um diesen zu bestimmen:
ein, um diesen zu bestimmen:
 2. Schritt: Berechnen der gesuchten Wahrscheinlichkeit
Soll der Wert von
2. Schritt: Berechnen der gesuchten Wahrscheinlichkeit
Soll der Wert von  um weniger als 10 vom Erwartungswert
um weniger als 10 vom Erwartungswert  abweichen so müssen folgende zwei Sachverhalte für Zufallsvariable
abweichen so müssen folgende zwei Sachverhalte für Zufallsvariable  erfüllt sein:
erfüllt sein:
 Diese Wahrscheinlichkeit kannst du nun wie oben mit deinem GTR berechnen. Da dieser aber nur Wahrscheinlichkeiten der Gestalt
Diese Wahrscheinlichkeit kannst du nun wie oben mit deinem GTR berechnen. Da dieser aber nur Wahrscheinlichkeiten der Gestalt  berechnen kann, musst du die hier vorliegende Wahrscheinlichkeit zunächst wie folgt umformen:
Berechne nun
berechnen kann, musst du die hier vorliegende Wahrscheinlichkeit zunächst wie folgt umformen:
Berechne nun  und
und  wie oben mit deinem GTR. Du solltest zu folgendem Ergebnis gekommen sein:
wie oben mit deinem GTR. Du solltest zu folgendem Ergebnis gekommen sein:
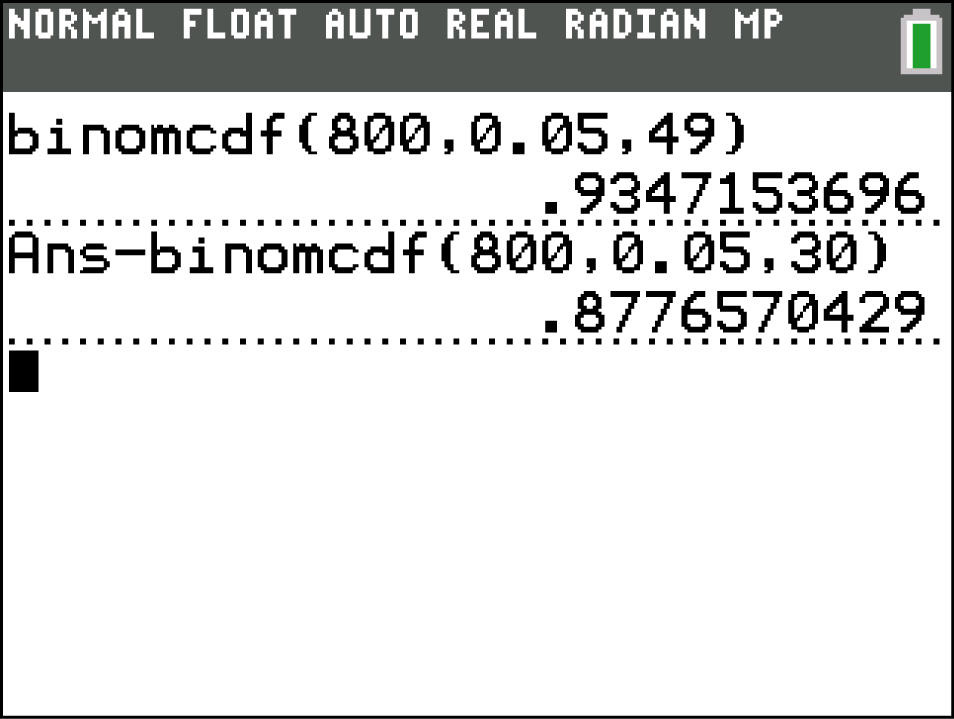 Mit einer Wahrscheinlichkeit von 0,8777 bzw. 87,77 % weicht der Wert von
Mit einer Wahrscheinlichkeit von 0,8777 bzw. 87,77 % weicht der Wert von  um weniger als 10 vom Erwartungswert ab.
um weniger als 10 vom Erwartungswert ab.
Da die Zufallsvariable
- „Stift ist fehlerhaft“ und
- „Stift ist nicht fehlerhaft“
Willst du die hier gesuchte Wahrscheinlichkeit mit deinem GTR berechnen, so wechselst du zunächst in den Calculator-Modus deines GTR. In diesem wendest du dann den binomCdf-Befehl an, auf welchen du über
|
2ND |
zugreifst. Willst du die Wahrscheinlichkeit

: untere Grenze für die Wahrscheinlichkeit
: obere Grenze für die Wahrscheinlichkeit
muss größer 30 und
muss kleiner 50 sein.

b)  Bestimmen des Ablehnungsbereichs
Der Aufgabenstellung kannst du nun entnehmen, dass der Betrieb eine neue Maschine erwirbt, von der behauptet wird, dass höchstens 2 % der von ihr produzierten Stifte fehlerhaft sind. Diese Hypothese
Bestimmen des Ablehnungsbereichs
Der Aufgabenstellung kannst du nun entnehmen, dass der Betrieb eine neue Maschine erwirbt, von der behauptet wird, dass höchstens 2 % der von ihr produzierten Stifte fehlerhaft sind. Diese Hypothese  soll hier mit Hilfe eines Tests an 800 zufällig ausgewählten Stiften überprüft werden. Deine Aufgabe ist es dabei, zu bestimmen, ab welcher Anzahl von fehlerhaften Stiften man sich gegen die Hypothese entscheidet. Die Irrtumswahrscheinlichkeit soll hier maximal 5 % betragen.
soll hier mit Hilfe eines Tests an 800 zufällig ausgewählten Stiften überprüft werden. Deine Aufgabe ist es dabei, zu bestimmen, ab welcher Anzahl von fehlerhaften Stiften man sich gegen die Hypothese entscheidet. Die Irrtumswahrscheinlichkeit soll hier maximal 5 % betragen.
Betrachte dazu zunächst die Zufallsvariable . Zufallsvariable
. Zufallsvariable  beschreibt hier die Anzahl der fehlerhaften Bleistifte und ist mit gleicher Begründung wie oben näherungsweise binomialverteilt. Für diese gilt dabei
beschreibt hier die Anzahl der fehlerhaften Bleistifte und ist mit gleicher Begründung wie oben näherungsweise binomialverteilt. Für diese gilt dabei  und
und  . Da hier die Anzahl an fehlerhaften Bleistiften ermittelt werden soll, ab welcher nicht mehr angenommen wird, dass die Maschine eine Ausschussquote von 2 % hat, müssen hier die Hypothesen wie folgt lauten:
. Da hier die Anzahl an fehlerhaften Bleistiften ermittelt werden soll, ab welcher nicht mehr angenommen wird, dass die Maschine eine Ausschussquote von 2 % hat, müssen hier die Hypothesen wie folgt lauten:
 entscheidet, suchst du hier den Ablehnungsbereich für die Hypothese
entscheidet, suchst du hier den Ablehnungsbereich für die Hypothese  :
:
 zu bestimmen. Bestimme diesen über die Irrtumswahrscheinlichkeit bzw. über die Wahrscheinlichkeit für den Fehler 1. Art.
zu bestimmen. Bestimme diesen über die Irrtumswahrscheinlichkeit bzw. über die Wahrscheinlichkeit für den Fehler 1. Art.
Der Ablehnungsbereich wird hier über die kleinste natürliche Zahl bestimmt, für welche folgender Zusammenhang noch erfüllt ist: Füge nun die linke Seite der Gleichung als Funktion in den Y=-Editor deines GTR ein, denke dabei daran, dass
Füge nun die linke Seite der Gleichung als Funktion in den Y=-Editor deines GTR ein, denke dabei daran, dass  und
und  gelten muss (linke Abbildung). Wechsle nun ins Table-Menü und suche die Stelle, an welcher zum ersten Mal
gelten muss (linke Abbildung). Wechsle nun ins Table-Menü und suche die Stelle, an welcher zum ersten Mal
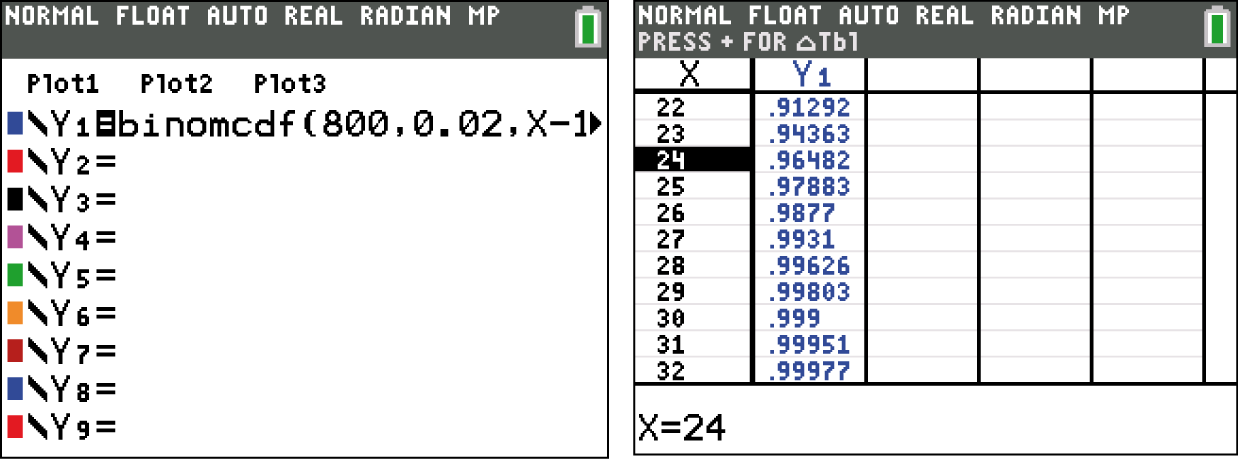 Da für X = 24 das erste mal die Aussage erfüllt ist, gilt hier für den Ablehnungsbereich:
Da für X = 24 das erste mal die Aussage erfüllt ist, gilt hier für den Ablehnungsbereich:
Betrachte dazu zunächst die Zufallsvariable
- Ablehnungsbereich:
.
Der Ablehnungsbereich wird hier über die kleinste natürliche Zahl bestimmt, für welche folgender Zusammenhang noch erfüllt ist:
.

- Ablehnungsbereich:
.
Lösung B2.1
a)  Bestimmen der Koordinatengleichung der Ebene
Bestimmen der Koordinatengleichung der Ebene  , in der die Platte liegt
Der Aufgabenstellung kannst du entnehmen, dass die rechteckige Platte die folgenden Eckpunkte besitzt:
, in der die Platte liegt
Der Aufgabenstellung kannst du entnehmen, dass die rechteckige Platte die folgenden Eckpunkte besitzt:
 zu bestimmen, in welcher die rechteckige Platte liegt. Die Ebenengleichung in Koordinatenform einer Ebene baut sich dabei wie folgt auf:
zu bestimmen, in welcher die rechteckige Platte liegt. Die Ebenengleichung in Koordinatenform einer Ebene baut sich dabei wie folgt auf:
 mit:
mit:
 bestimmen, so bestimmst du zunächst den Normalenvektor
bestimmen, so bestimmst du zunächst den Normalenvektor  über das Kreuz- bzw. Vektorprodukt. Verwende dazu die Koordinaten der Eckpunkte der rechteckigen Platte.
über das Kreuz- bzw. Vektorprodukt. Verwende dazu die Koordinaten der Eckpunkte der rechteckigen Platte.
 über das Kreuzprodukt
Willst du den Normalenvektor
über das Kreuzprodukt
Willst du den Normalenvektor  der Ebene
der Ebene  bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene
bestimmen, so benötigst du zunächst 2 Vektoren, welche die Ebene  aufspannen. Gehe hier beispielsweise von Punkte
aufspannen. Gehe hier beispielsweise von Punkte  aus. Punkt
aus. Punkt  ist über eine Kante mit Punkt
ist über eine Kante mit Punkt  und
und  verbunden:
verbunden:
![\(\begin{array}[t]{rll}
\overrightarrow{AB} &=&\overrightarrow{OB} - \overrightarrow{OA} & \\[5pt]
&=& \begin{pmatrix}0 \\ 6 \\ 0\end{pmatrix} - \begin{pmatrix}10\\6\\0\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}0 &-& 10 \\ 6 &-& 6 \\ 0 &-& 0\end{pmatrix} & \\[5pt]
&=& \begin{pmatrix}-10 \\ 0 \\ 0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/dd61f4afb9ae8bcb124aaef1a5699fea71f158f86c1ca3e573ac3ed772b1c8be?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{AD}&=& \overrightarrow{OD} - \overrightarrow{OA}& \\[5pt]
&=& \begin{pmatrix}10 \\ 0 \\ 3\end{pmatrix} - \begin{pmatrix}10\\6\\0\end{pmatrix} & \\[5pt]
&=& \begin{pmatrix}10 &-& 10 \\ 0 &-& 6 \\ 3 &-& 0\end{pmatrix}& \\[5pt]
&=&\begin{pmatrix}0 \\ -6 \\ 3\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/7e0c555f2176daacf7a5c908a3d82bff1adabf083fd7fc47c8b0024749706870?color=5a5a5a) Berechne nun wie folgt das Kreuzprodukt der Vektoren
Berechne nun wie folgt das Kreuzprodukt der Vektoren  und
und  , um den Normalenvektor
, um den Normalenvektor  zu bestimmen:
Da beim Normalenvektor
zu bestimmen:
Da beim Normalenvektor  nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
nicht die Länge, sondern nur die Richtung entscheidend ist, ist hier folgende Umformung zulässig:
 2. Schritt: Bestimmen der Koordinatengleichung über eine Punktprobe
Setzt du nun den Normalenvektor
2. Schritt: Bestimmen der Koordinatengleichung über eine Punktprobe
Setzt du nun den Normalenvektor  in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
Die Konstante
in die allgemeine Koordinatengleichung von oben ein, so ergibt sich diese hier zu:
Die Konstante  bestimmst du hier nun, indem du beispielsweise die Koordinaten von
bestimmst du hier nun, indem du beispielsweise die Koordinaten von  mit
mit  für
für  ,
,  und
und  einsetzt und die Gleichung nach
einsetzt und die Gleichung nach  löst:
löst:
 Eine Koordinatengleichung der Ebene
Eine Koordinatengleichung der Ebene  lautet also:
lautet also:
 .
.
 Darstellen des Sachverhaltes in einem Koordinatensystem
Hier sollst du nun die Platte, den Stab und die Lichtquelle in einem Koordinatensystem darstellen. Orientiere dich beim Zeichnen der Achsen an den Koordinaten der einzuzeichnenden Punkte und denke daran, dass alle Koordinatenangaben in deinem Koordinatensystem in m sind. Zeichne zunächst die Platte mit:
Darstellen des Sachverhaltes in einem Koordinatensystem
Hier sollst du nun die Platte, den Stab und die Lichtquelle in einem Koordinatensystem darstellen. Orientiere dich beim Zeichnen der Achsen an den Koordinaten der einzuzeichnenden Punkte und denke daran, dass alle Koordinatenangaben in deinem Koordinatensystem in m sind. Zeichne zunächst die Platte mit:
 ein und von diesem dann einen 2 m langen Stab. Zuletzt zeichnest du die Lichtquelle
ein und von diesem dann einen 2 m langen Stab. Zuletzt zeichnest du die Lichtquelle  bei
bei  ein.
ein.
Deine Zeichnung sollte hier so aussehen:

 Bestimmen des Winkels zwischen Stab und Platte
Nun sollst du den Winkel
Bestimmen des Winkels zwischen Stab und Platte
Nun sollst du den Winkel  zwischen dem Stab bei
zwischen dem Stab bei  und der Platte
und der Platte  bestimmen. Da der Stab durch einen Vektor
bestimmen. Da der Stab durch einen Vektor  (siehe oben) und die Platte
(siehe oben) und die Platte  durch eine Ebene repräsentiert werden können, gilt es hier einen Winkel zwischen einer Ebene und einem Vektor zu berechnen.
durch eine Ebene repräsentiert werden können, gilt es hier einen Winkel zwischen einer Ebene und einem Vektor zu berechnen.
Für die Berechnung eines Winkels zwischen einem Vektor und einer Ebene gilt dabei folgendes: mit:
mit:
 der den Stab repräsentiert und bestimme dann mit dem Normalenvektor
der den Stab repräsentiert und bestimme dann mit dem Normalenvektor  der Ebene
der Ebene  den hier gesuchten Winkel.
den hier gesuchten Winkel.
Da der Stab 2 m lang ist und in positive -Richtung zeigt, ergibt sich der Vektor
-Richtung zeigt, ergibt sich der Vektor  hier wie folgt:
hier wie folgt:
 Setze nun
Setze nun  und
und  in den Zusammenhang von oben ein, um den hier gesuchten Winkel
in den Zusammenhang von oben ein, um den hier gesuchten Winkel  zu bestimmen:
Der Winkel zwischen Stab und Platte beträgt also ungefähr 63,4°.
zu bestimmen:
Der Winkel zwischen Stab und Platte beträgt also ungefähr 63,4°.
;
;
und
.
,
und
: Einträge des Normalenvektors
der Ebene
: Über Punktprobe zu bestimmende Konstante
Hast du den Normalenvektor  der Ebene
der Ebene  bestimmt, so bestimmst du über eine Punktprobe die Konstante
bestimmt, so bestimmst du über eine Punktprobe die Konstante  . Verwende dazu die Koordinaten von Punkt
. Verwende dazu die Koordinaten von Punkt  ,
,  ,
,  oder
oder  .
.
1. Schritt: Bestimmen des Normalenvektors ;
;
und
.
Deine Zeichnung sollte hier so aussehen:

Für die Berechnung eines Winkels zwischen einem Vektor und einer Ebene gilt dabei folgendes:
: Betrachteter Vektor;
: Normalenvektor der betrachteten Ebene.
Da der Stab 2 m lang ist und in positive
b)  Berechnen des Schattenpunktes des oberen Endes des Stabes
Der Aufgabenstellung kannst du entnehmen, dass sich im Punkt
Berechnen des Schattenpunktes des oberen Endes des Stabes
Der Aufgabenstellung kannst du entnehmen, dass sich im Punkt  eine punktförmige Lichtquelle befindet. Weiterhin weißt du, dass der Stab einen Schatten auf die Platte wirft. Deine Aufgabe ist es dabei, die Koordinaten des Schattenpunktes
eine punktförmige Lichtquelle befindet. Weiterhin weißt du, dass der Stab einen Schatten auf die Platte wirft. Deine Aufgabe ist es dabei, die Koordinaten des Schattenpunktes  des oberen Endes des Stabes, welcher dieser auf die Platte wirft, zu bestimmen.
des oberen Endes des Stabes, welcher dieser auf die Platte wirft, zu bestimmen.
Aus dem vorhergegangenen Aufgabenteil weißt du, dass das obere Ende des Stabes die Koordinaten besitzt. Nun werden von Punkt
besitzt. Nun werden von Punkt  aus Lichtstrahlen in Richtung des Stabes geworfen. Das heißt, die „Richtung des Schattens“ des oberen Endes des Stabes wird durch den Vektor
aus Lichtstrahlen in Richtung des Stabes geworfen. Das heißt, die „Richtung des Schattens“ des oberen Endes des Stabes wird durch den Vektor  bestimmt. Willst du nun ausgehend von dem Wissen über diesen Vektor den Schattenpunkt
bestimmt. Willst du nun ausgehend von dem Wissen über diesen Vektor den Schattenpunkt  bestimmen, so gehst du hier so vor:
bestimmen, so gehst du hier so vor:
 Soll Gerade
Soll Gerade  die Richtung des Lichtes, ausgehend von Punkt
die Richtung des Lichtes, ausgehend von Punkt  beschreiben, so muss diese den Vektor
beschreiben, so muss diese den Vektor  als Stütz- und den Vektor
als Stütz- und den Vektor  als Richtungsvektor besitzen.
als Richtungsvektor besitzen.
![\(\begin{array}[t]{rll}
\overrightarrow{LT}&=& \overrightarrow{OT} - \overrightarrow{OL} &\\[5pt]
&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} - \begin{pmatrix}8 \\ 10 \\ 2\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}5 &-& 8 \\ 6 &-& 10 \\ 2 &-& 2\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/f3e54cbb98e5f6d6fffc106812b214b8d31052ff9137e515b46b1d151008ec10?color=5a5a5a)
![\(\begin{array}[t]{rll}
l: \quad \overrightarrow{x} &=& \overrightarrow{OT} + t \cdot \overrightarrow{LT}&\\[5pt]
&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} + t \cdot \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/337088f1d403968d343b25119aae02dcd471bfcadbe6db687f9aa73dc4f76d6f?color=5a5a5a) 2. Schritt: Bestimmen des Schattenpunktes
2. Schritt: Bestimmen des Schattenpunktes  Willst du den Schnittpunkt von Ebene
Willst du den Schnittpunkt von Ebene  und Gerade
und Gerade  bestimmen, so formulierst du zunächst Gerade
bestimmen, so formulierst du zunächst Gerade  als einen einzelnen Vektor. Anschließend setzt du die Einträge dieses Vektors in die Koordinatengleichung von
als einen einzelnen Vektor. Anschließend setzt du die Einträge dieses Vektors in die Koordinatengleichung von  ein und berechnest den zu
ein und berechnest den zu  zugehörigen Parameterwert von
zugehörigen Parameterwert von  .
.
![\(\begin{array}[t]{rll}
l: \quad \overrightarrow{x_l}&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} + t \cdot \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}5 - 3 \cdot t \\ 6 - 4 \cdot t \\ 2\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/db7cda6f53ce90404abadb996d5412cc675cece47a3d654d73ab3b5c8d393c78?color=5a5a5a) Ein Einsetzen von
Ein Einsetzen von  in die Koordinatengleichung von
in die Koordinatengleichung von  , für
, für  ,
,  und
und  ergibt:
ergibt:
 Setze nun
Setze nun  in die Geradengleichung von
in die Geradengleichung von  ein, um die Koordinaten von Schattenpunkt
ein, um die Koordinaten von Schattenpunkt  zu bestimmen:
zu bestimmen:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=& \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix} + 1 \cdot \begin{pmatrix}-3 \\ -4 \\ 0\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}5 &-& 3 \\ 6 &-& 4 \\ 2 &+& 0\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}2 \\ 2 \\ 2\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/3a7b22251d72978d9be8afdecc59a72818009ee197e6d98075b10eaa27cbdf44?color=5a5a5a) Der Schattenpunkt des oberen Endes des Stabes hat die Koordinaten:
Der Schattenpunkt des oberen Endes des Stabes hat die Koordinaten:  .
.
 Begründen, dass der Schatten vollständig auf der Platte liegt
Nun sollst du begründen, dass der Schatten, den der Stab wirft, sich vollständig auf der Platte befindet. Von oben weißt du, dass der Schattenpunkt, welcher vom oberen Ende des Stabes geworfen wird, die Koordinaten
Begründen, dass der Schatten vollständig auf der Platte liegt
Nun sollst du begründen, dass der Schatten, den der Stab wirft, sich vollständig auf der Platte befindet. Von oben weißt du, dass der Schattenpunkt, welcher vom oberen Ende des Stabes geworfen wird, die Koordinaten  besitzt.
besitzt.
Willst du hier begründen, dass der Schatten, welcher vom Stab geworfen wird, sich vollständig auf der Platte befindet, so musst du hier folgendes tun: mit den Koordinaten der Eckpunkte
mit den Koordinaten der Eckpunkte  ,
,  ,
,  und
und  , so kannst du hier folgendes feststellen:
, so kannst du hier folgendes feststellen:
 liegt also offensichtlich auf der Platte. Da auch der Anfangspunkt
liegt also offensichtlich auf der Platte. Da auch der Anfangspunkt  mit
mit  des Stabes sich auf der Platte befindet, muss sich der Schatten zwischen
des Stabes sich auf der Platte befindet, muss sich der Schatten zwischen  und
und  ebenfalls auf der Platte befinden. Dies lässt sich auch wie folgt an der Zeichnung aus a veranschaulichen:
ebenfalls auf der Platte befinden. Dies lässt sich auch wie folgt an der Zeichnung aus a veranschaulichen:
 Der Schatten wurde hier in rot eingezeichnet.
Der Schatten wurde hier in rot eingezeichnet.
Aus dem vorhergegangenen Aufgabenteil weißt du, dass das obere Ende des Stabes die Koordinaten
- Formuliere eine Gerade
, die die Richtung des Lichtes ausgehend vom Punkt
beschreibt.
- Schneide die Gerade mit der Ebene
, die die Platte repräsentiert
- Der Schnittpunkt von Gerade
und Ebene
ist dann der gesuchte Schattenpunkt
.
Willst du hier begründen, dass der Schatten, welcher vom Stab geworfen wird, sich vollständig auf der Platte befindet, so musst du hier folgendes tun:
- Vergleiche die Koordinaten von Punkt
mit den Koordinaten der Eckpunkte der Platte.
- Analysiere die Koordinaten von Punkt
nochmals genauer und setze sie in Relation zu den Koordinaten von
.
- Veranschauliche deine Überlegungen an der Skizze aus Aufgabenteil a.
- Der Schattenpunkt
liegt in der Ebene
.
- Die
-Koordinate von
liegt zwischen den
-Koordinaten von
und
.
- Die
-Koordinate von
liegt zwischen den
-Koordinaten von
und
.

c)  Berechnen der Koordinaten der möglichen Kollisionspunkte
Der Aufgabenstellung kannst du nun entnehmen, dass sich die Lichtquelle von
Berechnen der Koordinaten der möglichen Kollisionspunkte
Der Aufgabenstellung kannst du nun entnehmen, dass sich die Lichtquelle von  aus auf einer zur
aus auf einer zur  -Ebene parallelen Kreisbahn bewegt. Der Mittelpunkt dieser Kreisbahn ist dabei Punkt
-Ebene parallelen Kreisbahn bewegt. Der Mittelpunkt dieser Kreisbahn ist dabei Punkt  , also das obere Ende des Stabes. Bewegt sich die Lichtquelle wie eben beschrieben auf der Kreisbahn, so kollidiert diese mit der Platte
, also das obere Ende des Stabes. Bewegt sich die Lichtquelle wie eben beschrieben auf der Kreisbahn, so kollidiert diese mit der Platte  . Deine Aufgabe ist es nun, die Koordinaten dieser möglichen Kollisionspunkte zu berechnen.
. Deine Aufgabe ist es nun, die Koordinaten dieser möglichen Kollisionspunkte zu berechnen.
Willst du hier die möglichen Kollisionspunkte bestimmen, so bestimmst du zunächst die Ebene , auf welcher sich die Lichtquelle bewegt. Beachte dabei, dass diese parallel zur
, auf welcher sich die Lichtquelle bewegt. Beachte dabei, dass diese parallel zur  -Ebene verlaufen muss.
-Ebene verlaufen muss.
Hast du Ebene bestimmt, so schneidest du diese mit der Ebene
bestimmt, so schneidest du diese mit der Ebene  , in welcher sich auch die Platte befindet. Da du hier zwei Ebenen schneidest, ergibt sich als Resultat eine Schnittgerade. Auf dieser Schnittgeraden müssen sich dann die möglichen Kollisionspunkte befinden. Überlege dir folgendes, um diese dann zu bestimmen:
, in welcher sich auch die Platte befindet. Da du hier zwei Ebenen schneidest, ergibt sich als Resultat eine Schnittgerade. Auf dieser Schnittgeraden müssen sich dann die möglichen Kollisionspunkte befinden. Überlege dir folgendes, um diese dann zu bestimmen:
 Wie oben beschrieben, müssen die gesuchten Kollisionspunkte auf der Schnittgeraden liegen, welche sich ergibt, wenn du Ebene
Wie oben beschrieben, müssen die gesuchten Kollisionspunkte auf der Schnittgeraden liegen, welche sich ergibt, wenn du Ebene  und Ebene
und Ebene  schneidest. Da die Kreisbahn parallel zur
schneidest. Da die Kreisbahn parallel zur  -Ebene sein soll, muss die Ebene, in welcher sie sich befindet, ebenfalls parallel zur
-Ebene sein soll, muss die Ebene, in welcher sie sich befindet, ebenfalls parallel zur  -Ebene sein.
-Ebene sein.
Betrachtest du die Koordinaten von und
und  genauer, so kannst du erkennen, dass beide eine
genauer, so kannst du erkennen, dass beide eine  -Koordinate von
-Koordinate von  haben. Da nun Punkt
haben. Da nun Punkt  und Punkt
und Punkt  in der Ebene
in der Ebene  liegen sollen und diese darüber hinaus auch noch parallel zur
liegen sollen und diese darüber hinaus auch noch parallel zur  -Ebene sein soll, lautet eine Koordinatengleichung dieser Ebene:
-Ebene sein soll, lautet eine Koordinatengleichung dieser Ebene:
 .
Willst du nun die Schnittgerade
.
Willst du nun die Schnittgerade  bestimmen, so formulierst du aus den Koordinatengleichungen von
bestimmen, so formulierst du aus den Koordinatengleichungen von  und
und  ein unterbesetztes Gleichungssystem. Führe in diesem Gleichungssystem für
ein unterbesetztes Gleichungssystem. Führe in diesem Gleichungssystem für  einen Parameter ein, um es eindeutig lösen zu können:
Gib nun die Lösungsmenge des LGS an und formuliere aus dieser wie folgt die Gerade
einen Parameter ein, um es eindeutig lösen zu können:
Gib nun die Lösungsmenge des LGS an und formuliere aus dieser wie folgt die Gerade  :
:
![\(\begin{array}[t]{rll}
\mathbb L &=& \left\{\begin{pmatrix}r \\ 2 \\ 2\end{pmatrix}\right\}\;& \\[5pt]
&=& \; \left\{\begin{pmatrix}0 \\ 2 \\ 2\end{pmatrix} + r \cdot \begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix}\right\}
\end{array}\)](https://mathjax.schullv.de/df60e25c675592e8c48180868c03ed9b6380894392ecf844cb99e413ef1ee347?color=5a5a5a) Schnittgerade
Schnittgerade  hat also folgende Gleichung:
hat also folgende Gleichung:
 2. Schritt: Bestimmen der möglichen Kollisionspunkte Nun weißt du folgende zwei Dinge über die Lage der Kollisionspunkte:
2. Schritt: Bestimmen der möglichen Kollisionspunkte Nun weißt du folgende zwei Dinge über die Lage der Kollisionspunkte:
 liegen und einen Abstand von 5 zu
liegen und einen Abstand von 5 zu  besitzen. Formuliere dazu auch hier wieder Gerade
besitzen. Formuliere dazu auch hier wieder Gerade  als Vektor um:
als Vektor um:
![\(\begin{array}[t]{rll}
s:\quad \overrightarrow{x_S}&=& \overrightarrow{K_r} & \\[5pt]
&=& \begin{pmatrix}0 \\ 2 \\ 2\end{pmatrix} + r \cdot \begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}r \\ 2 \\ 2\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/140de7c62e96609d1d0a6da987346251034d10419a9c7954e55c1ab45894c72a?color=5a5a5a) Bestimmst du nun den Betrag des Vektors
Bestimmst du nun den Betrag des Vektors  , so hast du den von
, so hast du den von  abhängigen Abstand zwischen Punkt
abhängigen Abstand zwischen Punkt  und den Kollisionspunkten
und den Kollisionspunkten  . Setzt du diesen Abstand gleich 5 so kannst du wie folgt die Koordinaten der möglichen Kollisionspunkte bestimmen:
. Setzt du diesen Abstand gleich 5 so kannst du wie folgt die Koordinaten der möglichen Kollisionspunkte bestimmen:
![\(\begin{array}[t]{rll}
5&=& \left|\overrightarrow{TK_r}\right|& \\[5pt]
&=& \left|\begin{pmatrix}r \\ 2 \\ 2\end{pmatrix} - \begin{pmatrix}5 \\ 6 \\ 2\end{pmatrix}\right|& \\[5pt]
&=&\left|\begin{pmatrix}r - 5 \\ -4 \\ 0\end{pmatrix}\right| & \\[5pt]
&=& \sqrt{(r - 5)^2 + (-4)^2 + 0^2}& \\[5pt]
&=& \sqrt{(r - 5)^2 + 16}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7f42e6a17b12dfeee87eeece375ed78ab1b53ac49589f300f2be3dcb08e453ea?color=5a5a5a) Diese Gleichung kannst du nun graphisch mit Hilfe deines GTR lösen. Übertrage die rechte Seite dazu in das GRAPH-Menü, als eine von x-abhängige Gleichung. Lasse dir den Graph anzeigen und bestimme über die folgende Eingabenfolge den Wert für
Diese Gleichung kannst du nun graphisch mit Hilfe deines GTR lösen. Übertrage die rechte Seite dazu in das GRAPH-Menü, als eine von x-abhängige Gleichung. Lasse dir den Graph anzeigen und bestimme über die folgende Eingabenfolge den Wert für  , an welchem die Gleichung den Wert 5 annimmt:
, an welchem die Gleichung den Wert 5 annimmt:
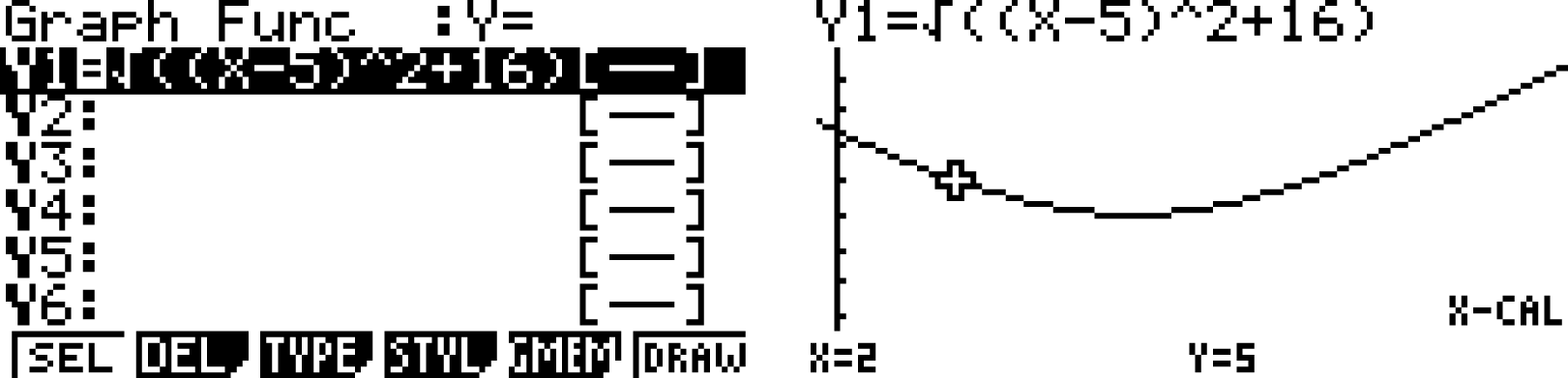 Als Lösung der Gleichung hat sich also ergeben:
Als Lösung der Gleichung hat sich also ergeben:  und
und  . Setze diese nun in die allgemeinen Koordinaten von
. Setze diese nun in die allgemeinen Koordinaten von  ein, so ergeben sich folgende zwei möglich Kollisionspunkte:
ein, so ergeben sich folgende zwei möglich Kollisionspunkte:
Willst du hier die möglichen Kollisionspunkte bestimmen, so bestimmst du zunächst die Ebene
Hast du Ebene
- Die Kollisionspunkte müssen sich auf der Schnittgeraden befinden;
- der Radius der Kreisbahn wird durch den Abstand zwischen
und
bestimmt;
- da es sich beim Punkt
um den Mittelpunkt des Kreises handelt, muss der Abstand zwischen
und den Kollisionspunkten gerade dem Radius entsprechen.
- Verwende beim Berechnen die allgemeinen Koordinaten der Kollisionspunkte, die sich aus der Schnittgeraden ergeben.
Betrachtest du die Koordinaten von
- Sie liegen auf der Gerade
und
- sie besitzen zum Punkt
einen Abstand von 5 m.
|
F5 (G-Solv) |
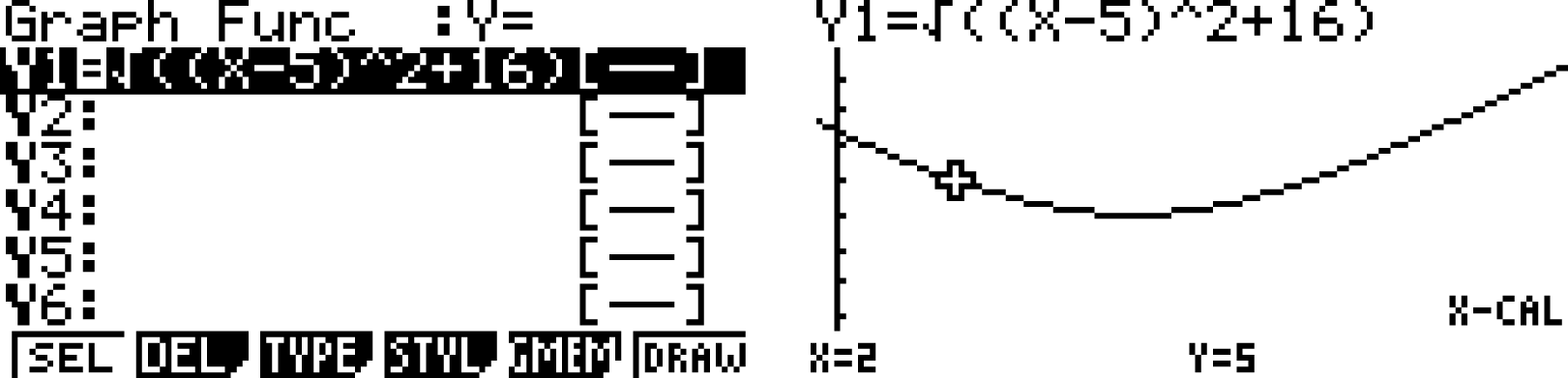
und
.
Lösung B2.2
a)  Berechnen der gesuchten Wahrscheinlichkeit
Der Aufgabenstellung kannst du entnehmen, dass bei der Produktion von Bleistiften erfahrungsgemäß der Anteil der fehlerhaften Stifte bei 5 % liegt. Nun werden der Produktion zur Qualitätsprüfung zufällig 800 Bleistifte entnommen. Die Zufallsvariable
Berechnen der gesuchten Wahrscheinlichkeit
Der Aufgabenstellung kannst du entnehmen, dass bei der Produktion von Bleistiften erfahrungsgemäß der Anteil der fehlerhaften Stifte bei 5 % liegt. Nun werden der Produktion zur Qualitätsprüfung zufällig 800 Bleistifte entnommen. Die Zufallsvariable  beschreibt dabei die Anzahl der fehlerhaften Stifte in der vorliegenden Stichprobe. Deine Aufgabe ist es nun, die Wahrscheinlichkeit
beschreibt dabei die Anzahl der fehlerhaften Stifte in der vorliegenden Stichprobe. Deine Aufgabe ist es nun, die Wahrscheinlichkeit  zu berechnen.
zu berechnen.
Da die Zufallsvariable nur die Ausprägungen
nur die Ausprägungen
 näherungsweise binomialverteilt. Für den Stichprobenumfang gilt
näherungsweise binomialverteilt. Für den Stichprobenumfang gilt  . Die Wahrscheinlichkeit
. Die Wahrscheinlichkeit  für einen fehlerhaften Stift ergibt sich aus dem relativen Anteil der fehlerhaften Stifte in der Produktion. Für
für einen fehlerhaften Stift ergibt sich aus dem relativen Anteil der fehlerhaften Stifte in der Produktion. Für  gilt also:
gilt also:
 Die hier gesuchte Wahrscheinlichkeit kannst du mit deinem GTR berechnen.
Die hier gesuchte Wahrscheinlichkeit kannst du mit deinem GTR berechnen.
Willst du die hier gesuchte Wahrscheinlichkeit mit deinem GTR berechnen, so wechselst du zunächst in den STAT-Modus deines GTR. In diesem wendest du dann den Binomial C,D-Befehl an, auf welchen du über
zugreifst. Willst du die Wahrscheinlichkeit hier berechnen, so wendest du den binomCdf-Befehl wie in den unten stehenden Schaubildern an.
hier berechnen, so wendest du den binomCdf-Befehl wie in den unten stehenden Schaubildern an.
 Für die Wahrscheinlichkeit
Für die Wahrscheinlichkeit  gilt also:
gilt also:  .
.
 Wahrscheinlichkeit, für die geg. Abweichung vom Erwartungswert
Hier sollst du nun die Wahrscheinlichkeit dafür bestimmen, dass der Wert von
Wahrscheinlichkeit, für die geg. Abweichung vom Erwartungswert
Hier sollst du nun die Wahrscheinlichkeit dafür bestimmen, dass der Wert von  um weniger als 10 vom Erwartungswert der Zufallsvariable
um weniger als 10 vom Erwartungswert der Zufallsvariable  abweicht. Bestimme dazu zunächst den Erwartungswert der Zufallsvariablen
abweicht. Bestimme dazu zunächst den Erwartungswert der Zufallsvariablen  . Der Erwartungswert einer binomialverteilten Zufallsvariablen ergibt sich dabei wie folgt:
. Der Erwartungswert einer binomialverteilten Zufallsvariablen ergibt sich dabei wie folgt:
 bestimmt, so formulierst du im nächsten Schritt die hier zu berechnende Wahrscheinlichkeit. Beachte dabei das hier eine Abweichung „nach oben“ und „nach unten“ beachtet werden muss. Die hier zu berechnende Wahrscheinlichkeit hat also diese Gestalt:
bestimmt, so formulierst du im nächsten Schritt die hier zu berechnende Wahrscheinlichkeit. Beachte dabei das hier eine Abweichung „nach oben“ und „nach unten“ beachtet werden muss. Die hier zu berechnende Wahrscheinlichkeit hat also diese Gestalt:
 mit:
mit:
 Setze
Setze  und
und  in die Formel für den Erwartungswert
in die Formel für den Erwartungswert  ein, um diesen zu bestimmen:
ein, um diesen zu bestimmen:
 2. Schritt: Berechnen der gesuchten Wahrscheinlichkeit
Soll der Wert von
2. Schritt: Berechnen der gesuchten Wahrscheinlichkeit
Soll der Wert von  um weniger als 10 vom Erwartungswert
um weniger als 10 vom Erwartungswert  abweichen so müssen folgende zwei Sachverhalte für Zufallsvariable
abweichen so müssen folgende zwei Sachverhalte für Zufallsvariable  erfüllt sein:
erfüllt sein:
 Diese Wahrscheinlichkeit kannst du nun wie oben mit deinem GTR berechnen. Da dieser aber nur Wahrscheinlichkeiten der Gestalt
Diese Wahrscheinlichkeit kannst du nun wie oben mit deinem GTR berechnen. Da dieser aber nur Wahrscheinlichkeiten der Gestalt  berechnen kann, musst du die hier vorliegende Wahrscheinlichkeit zunächst wie folgt umformen:
Berechne nun
berechnen kann, musst du die hier vorliegende Wahrscheinlichkeit zunächst wie folgt umformen:
Berechne nun  und
und  wie oben mit deinem GTR. Du solltest zu folgendem Ergebnis gekommen sein:
wie oben mit deinem GTR. Du solltest zu folgendem Ergebnis gekommen sein:
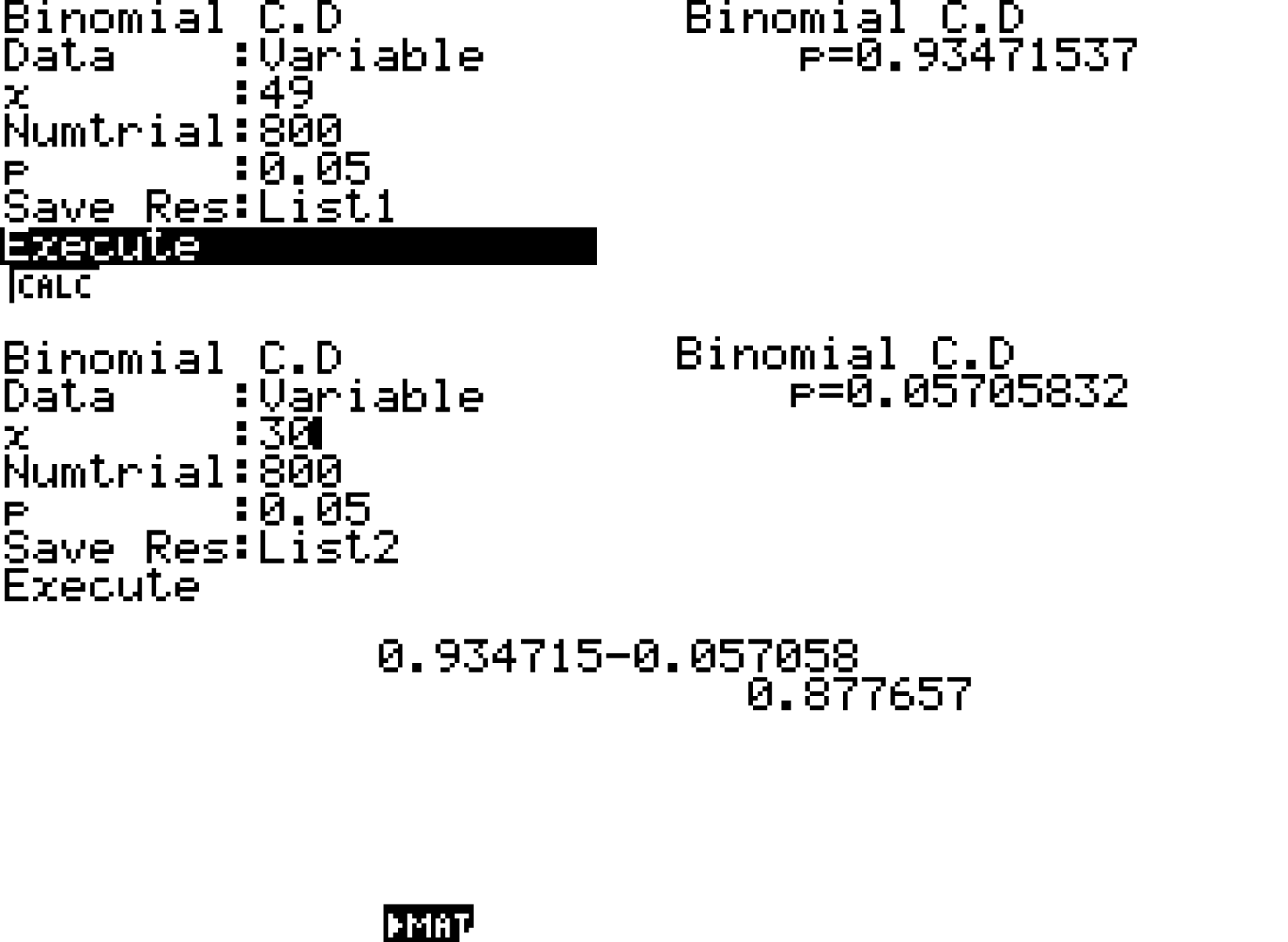 Mit einer Wahrscheinlichkeit von 0,8777 bzw. 87,77 % weicht der Wert von
Mit einer Wahrscheinlichkeit von 0,8777 bzw. 87,77 % weicht der Wert von  um weniger als 10 vom Erwartungswert ab.
um weniger als 10 vom Erwartungswert ab.
Da die Zufallsvariable
- „Stift ist fehlerhaft“ und
- „Stift ist nicht fehlerhaft“
Willst du die hier gesuchte Wahrscheinlichkeit mit deinem GTR berechnen, so wechselst du zunächst in den STAT-Modus deines GTR. In diesem wendest du dann den Binomial C,D-Befehl an, auf welchen du über
|
DIST |
zugreifst. Willst du die Wahrscheinlichkeit

: untere Grenze für die Wahrscheinlichkeit und
: obere Grenze für die Wahrscheinlichkeit.
muss größer 30 und
muss kleiner 50 sein

b)  Bestimmen des Ablehnungsbereichs
Der Aufgabenstellung kannst du nun entnehmen, dass der Betrieb eine neue Maschine erwirbt, von der behauptet wird, dass höchstens 2 % der von ihr produzierten Stifte fehlerhaft sind. Diese Hypothese
Bestimmen des Ablehnungsbereichs
Der Aufgabenstellung kannst du nun entnehmen, dass der Betrieb eine neue Maschine erwirbt, von der behauptet wird, dass höchstens 2 % der von ihr produzierten Stifte fehlerhaft sind. Diese Hypothese  soll hier mit Hilfe eines Tests an 800 zufällig ausgewählten Stiften überprüft werden. Deine Aufgabe ist es dabei, zu bestimmen, ab welcher Anzahl von fehlerhaften Stiften man sich gegen die Hypothese entscheidet. Die Irrtumswahrscheinlichkeit soll hier maximal 5 % betragen.
soll hier mit Hilfe eines Tests an 800 zufällig ausgewählten Stiften überprüft werden. Deine Aufgabe ist es dabei, zu bestimmen, ab welcher Anzahl von fehlerhaften Stiften man sich gegen die Hypothese entscheidet. Die Irrtumswahrscheinlichkeit soll hier maximal 5 % betragen.
Betrachte dazu zunächst die Zufallsvariable . Zufallsvariable
. Zufallsvariable  beschreibt hier die Anzahl der fehlerhaften Bleistifte und ist mit gleicher Begründung wie oben näherungsweise binomialverteilt. Für diese gilt dabei
beschreibt hier die Anzahl der fehlerhaften Bleistifte und ist mit gleicher Begründung wie oben näherungsweise binomialverteilt. Für diese gilt dabei  und
und  . Da hier die Anzahl an fehlerhaften Bleistiften ermittelt werden soll, ab welcher nicht mehr angenommen wird, dass die Maschine eine Ausschussquote von 2 % hat, müssen hier die Hypothesen wie folgt lauten:
. Da hier die Anzahl an fehlerhaften Bleistiften ermittelt werden soll, ab welcher nicht mehr angenommen wird, dass die Maschine eine Ausschussquote von 2 % hat, müssen hier die Hypothesen wie folgt lauten:
 entscheidet, suchst du hier den Ablehnungsbereich für die Hypothese
entscheidet, suchst du hier den Ablehnungsbereich für die Hypothese  :
Ablehnungsbereich:
:
Ablehnungsbereich:  Um diese Aufgabe zu lösen, gilt es hier also den Ablehnungsbereich
Um diese Aufgabe zu lösen, gilt es hier also den Ablehnungsbereich  zu bestimmen. Bestimme diesen über die Irrtumswahrscheinlichkeit bzw. über die Wahrscheinlichkeit für den Fehler 1. Art.
zu bestimmen. Bestimme diesen über die Irrtumswahrscheinlichkeit bzw. über die Wahrscheinlichkeit für den Fehler 1. Art.
Der Ablehnungsbereich wird hier über die kleinste natürliche Zahl bestimmt, für welche folgender Zusammenhang noch erfüllt ist: Diese Ungleichung kannst du nun mit deinem GTR lösen. Forme diese dazu zunächst wie folgt um:
Diese Ungleichung kannst du nun mit deinem GTR lösen. Forme diese dazu zunächst wie folgt um:
 Diese Ungleichung kannst du nun über systematischen Probieren mit deinem GTR berechnen. Wechsle dazu in den STAT-Modus und erstelle da eine Tabelle mit den Werten von z.B. 1 bis 50 (Abbildung links). Wechsle dann in das Menü für den Binomial C,D-Befehl und gib für n = 800 und p = 0, 02 ein. Den Befehl wendest du auf die Spalte in der Tabelle an, in welcher du die Werte von 1 bis 50 gespeichert hast (hier List 1). Speichere das Resultat in der zweiten Spalte der Tabelle (List 2, siehe Abb. in der Mitte). Suche zu letzt im Resultat nach jenem Wert, an welchem X erstmals größer als 0,95 ist (Abb. rechts).
Diese Ungleichung kannst du nun über systematischen Probieren mit deinem GTR berechnen. Wechsle dazu in den STAT-Modus und erstelle da eine Tabelle mit den Werten von z.B. 1 bis 50 (Abbildung links). Wechsle dann in das Menü für den Binomial C,D-Befehl und gib für n = 800 und p = 0, 02 ein. Den Befehl wendest du auf die Spalte in der Tabelle an, in welcher du die Werte von 1 bis 50 gespeichert hast (hier List 1). Speichere das Resultat in der zweiten Spalte der Tabelle (List 2, siehe Abb. in der Mitte). Suche zu letzt im Resultat nach jenem Wert, an welchem X erstmals größer als 0,95 ist (Abb. rechts).
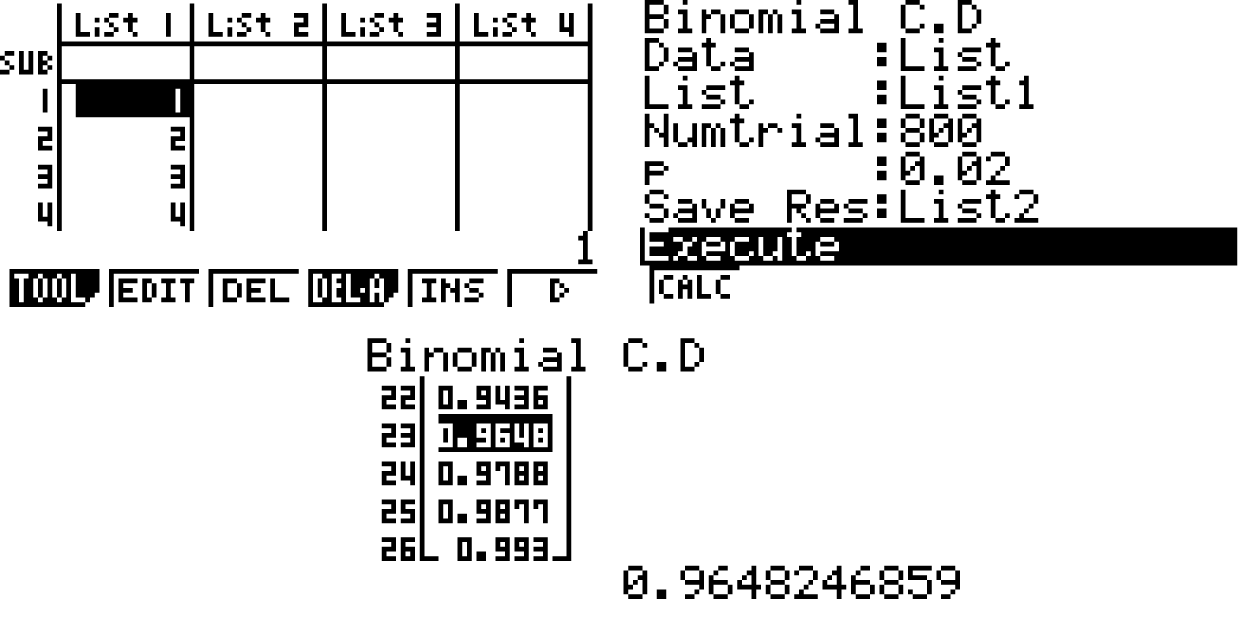 Für X = 23 ist hier der Wert erstmals größer 0,95. Da hier zur Berechnung g ? 1 ignoriert wurde, muss X um 1 erhöht werden, um den Ablehnungsbereich korrekt zu bestimmen. Das heißt, für X = 24 ist das erste mal die Aussage erfüllt. Für den Ablehnungsbereich gilt hier:
Ablehnungsbereich:
Für X = 23 ist hier der Wert erstmals größer 0,95. Da hier zur Berechnung g ? 1 ignoriert wurde, muss X um 1 erhöht werden, um den Ablehnungsbereich korrekt zu bestimmen. Das heißt, für X = 24 ist das erste mal die Aussage erfüllt. Für den Ablehnungsbereich gilt hier:
Ablehnungsbereich:  Das heißt, bei mindestens 24 fehlerhaften Stiften entscheidet man sich gegen die Nullhypothese.
Das heißt, bei mindestens 24 fehlerhaften Stiften entscheidet man sich gegen die Nullhypothese.
Betrachte dazu zunächst die Zufallsvariable
Der Ablehnungsbereich wird hier über die kleinste natürliche Zahl bestimmt, für welche folgender Zusammenhang noch erfüllt ist:
