Analytische Geometrie

Aufgabe II 1

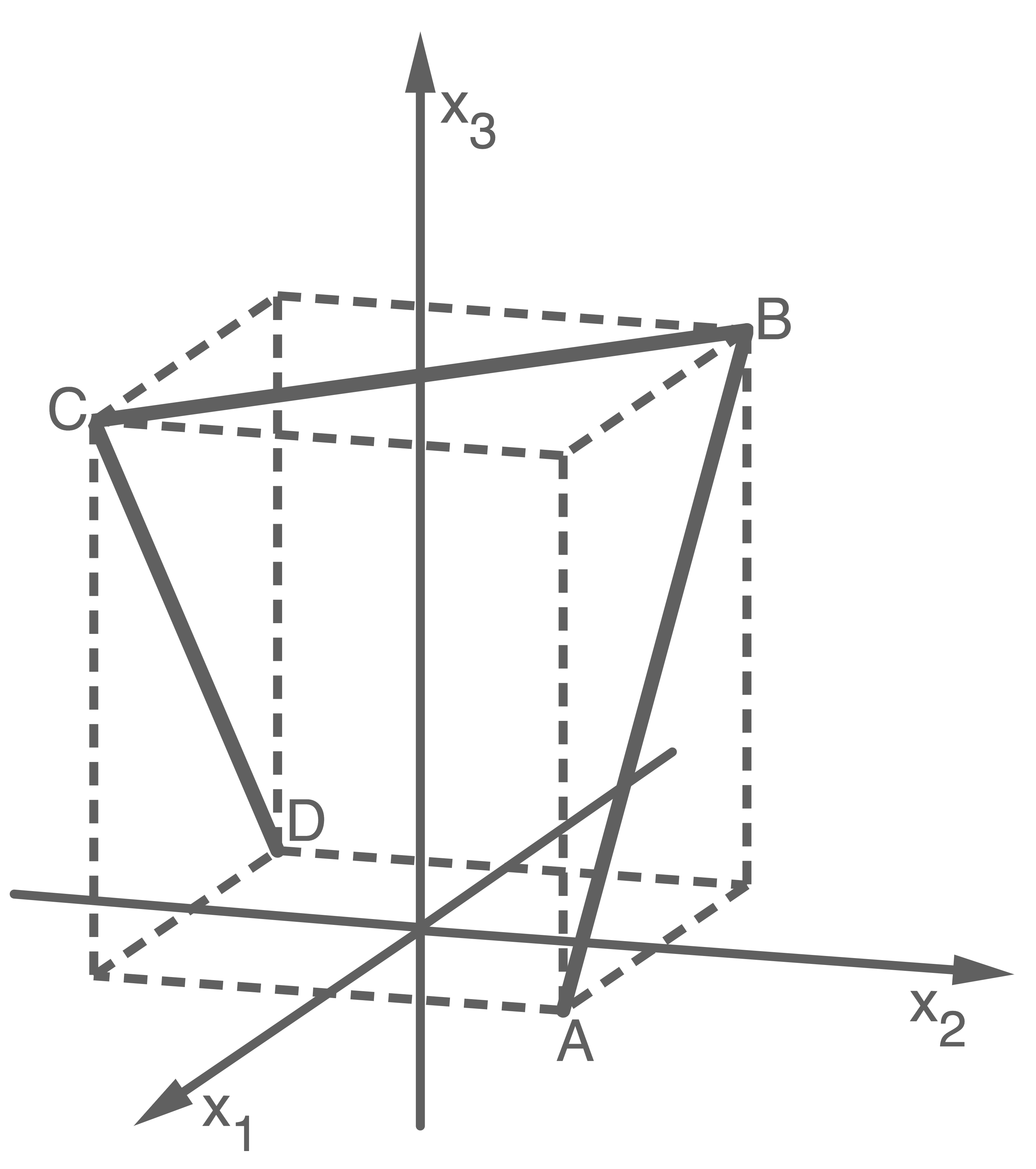
Im Koordinatensystem ist der Streckenzug abgebildet, der aus den Strecken $\overline{A B},$ $\overline{B C}$ und $\overline{C D}$ besteht mit $A(11\mid 11\mid 0),$ $B(-11\mid 11\mid 28),$ $C(11\mid -11\mid 28)$ und $D(-11\mid -11\mid 0).$

Die Punkte $A,$ $B,$ $C$ und $D$ sind Eckpunkte eines Quaders, der gestrichelt dargestellt ist.

Quader - Schleswig-Holstein Abi 2022 (Analytische Geometrie)

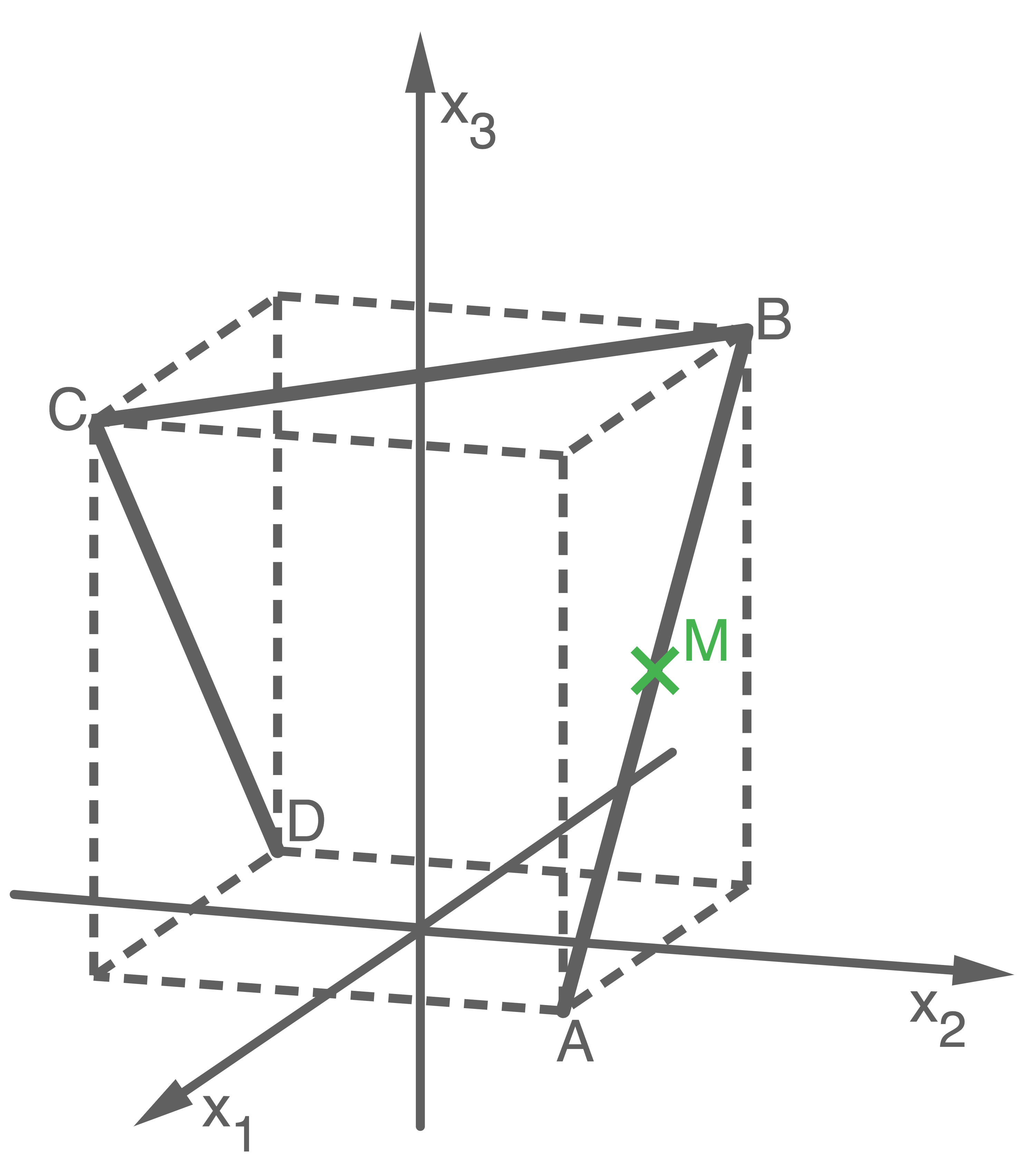
Zeichne den Mittelpunkt $M$ der Strecke $\overline{A B}$ in die obige Abbildung und gib seine Koordinaten an.

(2 BE)

Prüfe rechnerisch, ob der Punkt $N(-9\mid -11\mid 3)$ auf der Strecke $\overline{C D}$ liegt.

(5 BE)

Berechne die Länge des abgebildeten Streckenzuges.

(3 BE)

Die Ebene $E$ enthält die Punkte $A,$ $B$ und $C.$

Bestimme eine Gleichung von $E$ in Koordinatenform.

[Kontrolle: $\left.\quad 14 x_{1}+14 x_{2}+11 x_{3}=308\right]$

(4 BE)

Der Abstand des Punktes $D$ von der Ebene $E$ wird mit $d$ bezeichnet.

Berechne den Wert von $d$ .
Begründe, dass der Term $\frac{d}{6} \cdot|\overrightarrow{A B} \times \overrightarrow{B C}|$ das Volumen der Pyramide $A B C D$ angibt.

(6 BE)

Berechne die Größe $\varphi$ des Winkels, unter dem $E$ die $x_{1} x_{2}$ -Ebene schneidet.

(4 BE)

Für jede reelle Z a h l $h$ wird der Punkt $P_{h}(0\mid 0\mid h)$ betrachtet.

Beschreibe die Lage des Punktes $P_{h}$ für $0 \lt h\lt 28.$

(2 BE)

Bestimme die beiden Werte von $h,$ so dass ein Dreieck $B P_{h} C$ mit rechtem Winkel bei $P_{h}$ vorliegt, und gib alle Werte von $h$ an, für die sich ein stumpfwinkliges Dreieck $B P_{h} C$ ergibt.

(6 BE)

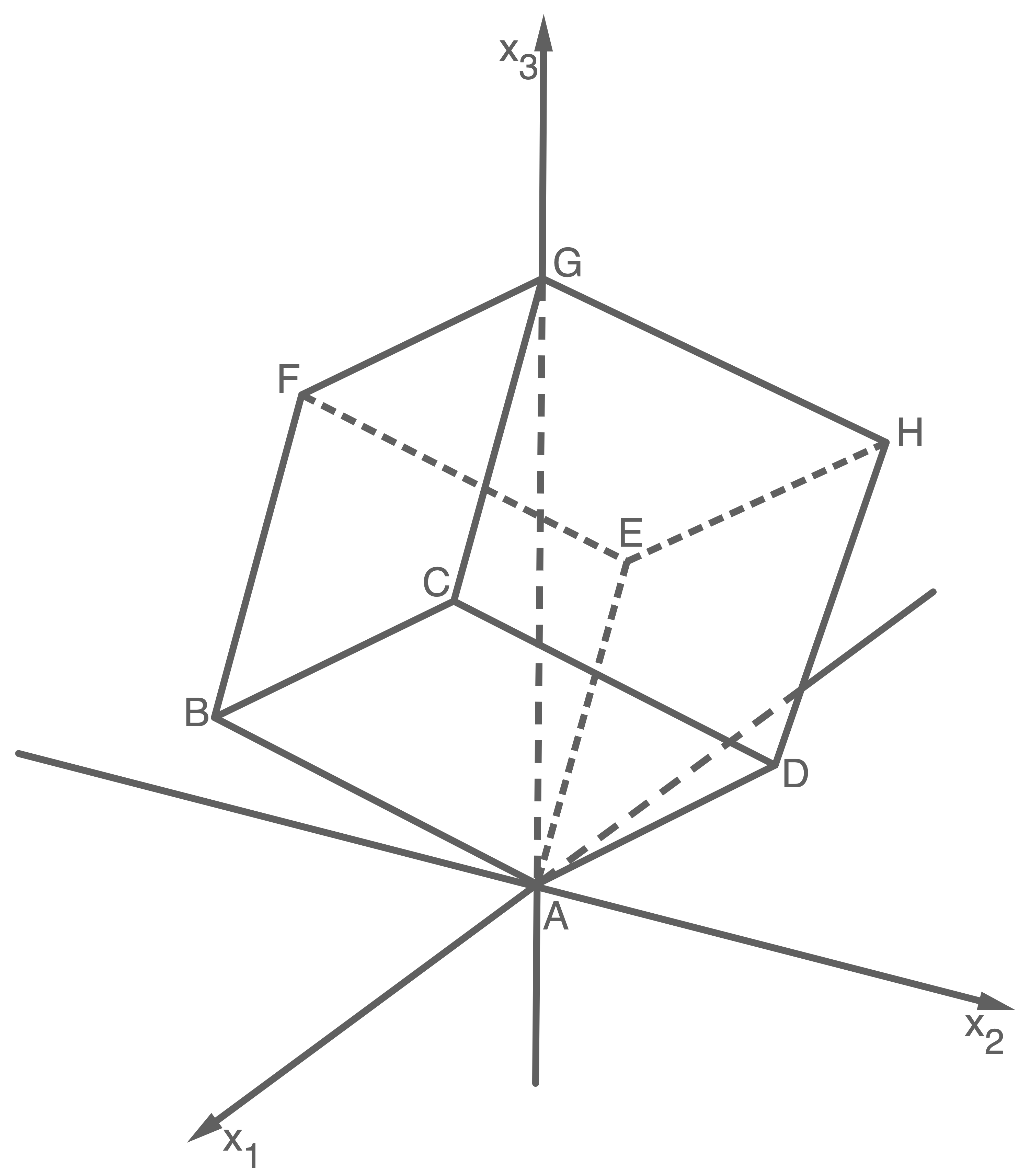
Aufgabe II 2

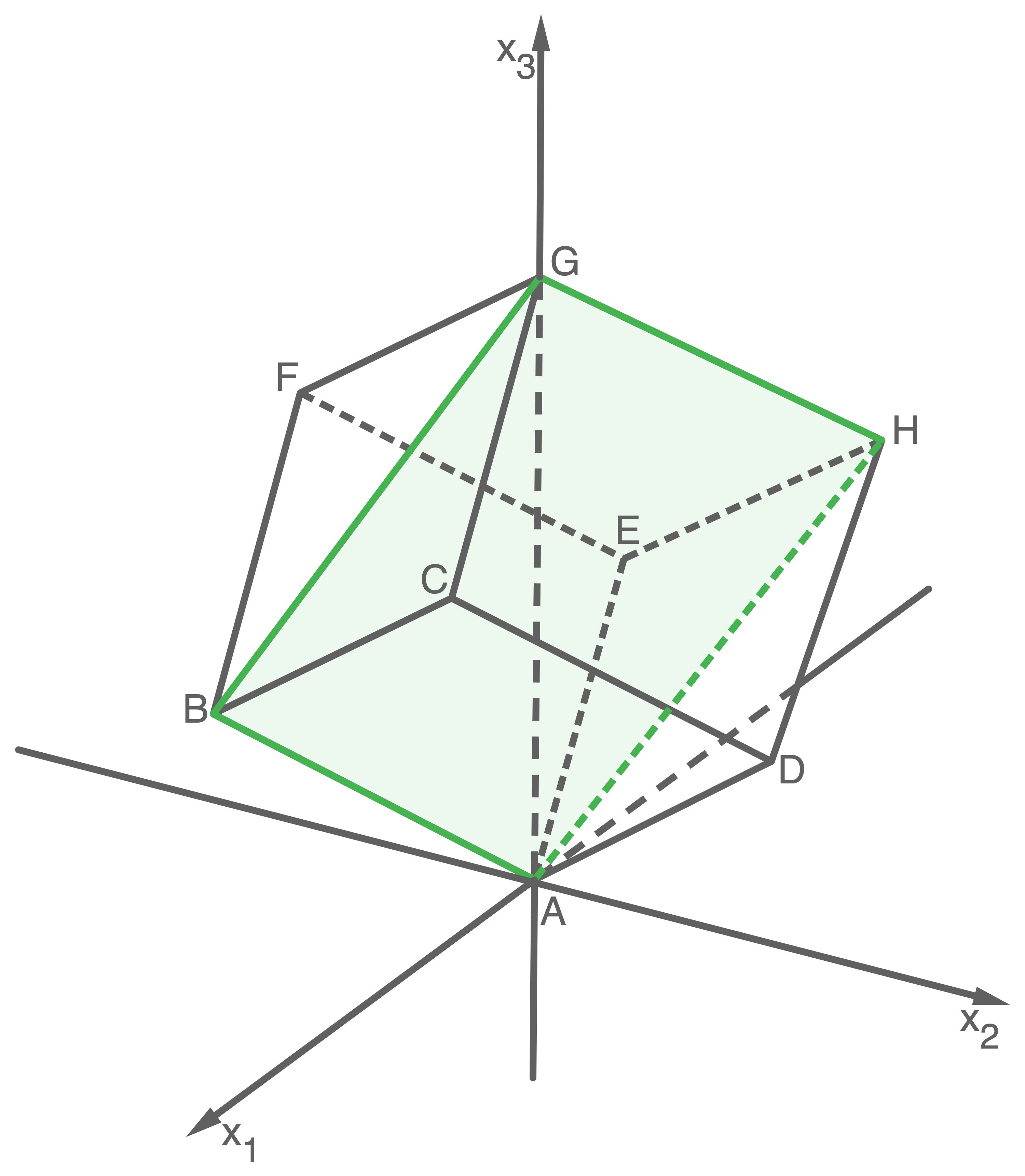
Betrachtet wird der abgebildete Würfel mit $A \left(0 \mid 0\mid 0\right),$ $B\left(3\mid -3 \mid 3\right),$ $G \left(0 \mid 0\mid 9\right)$ und $H\left(-3 \mid 3\mid 6\right).$

Berechne das Volumen des Würfels.

(2 BE)

Begründe, dass das Viereck $ABGH$ ein Rechteck ist, und zeichne dieses in die Abbildung ein.

(3 BE)

Das Viereck $ABGH$ liegt in der Ebene $L.$
Bestimme eine Gleichung von $L$ in Parameterform und Koordinatenform.

[Kontrollergebnis: $x_1 + x_2 = 0$ ]

(5 BE)

Bestimme die Größe des Winkels, den die Ebene $L$ mit der $x_1x_3$ -Ebene einschließt.

(2 BE)

Ermittle die Koordinaten von $F$ .

(5 BE)

Die Ebene, die durch die Mittelpunkte der Kanten $\overline{BC},\overline{CG},\overline{AD}$ und $\overline{DH}$ verläuft, teilt den Würfel in zwei Teilkörper.
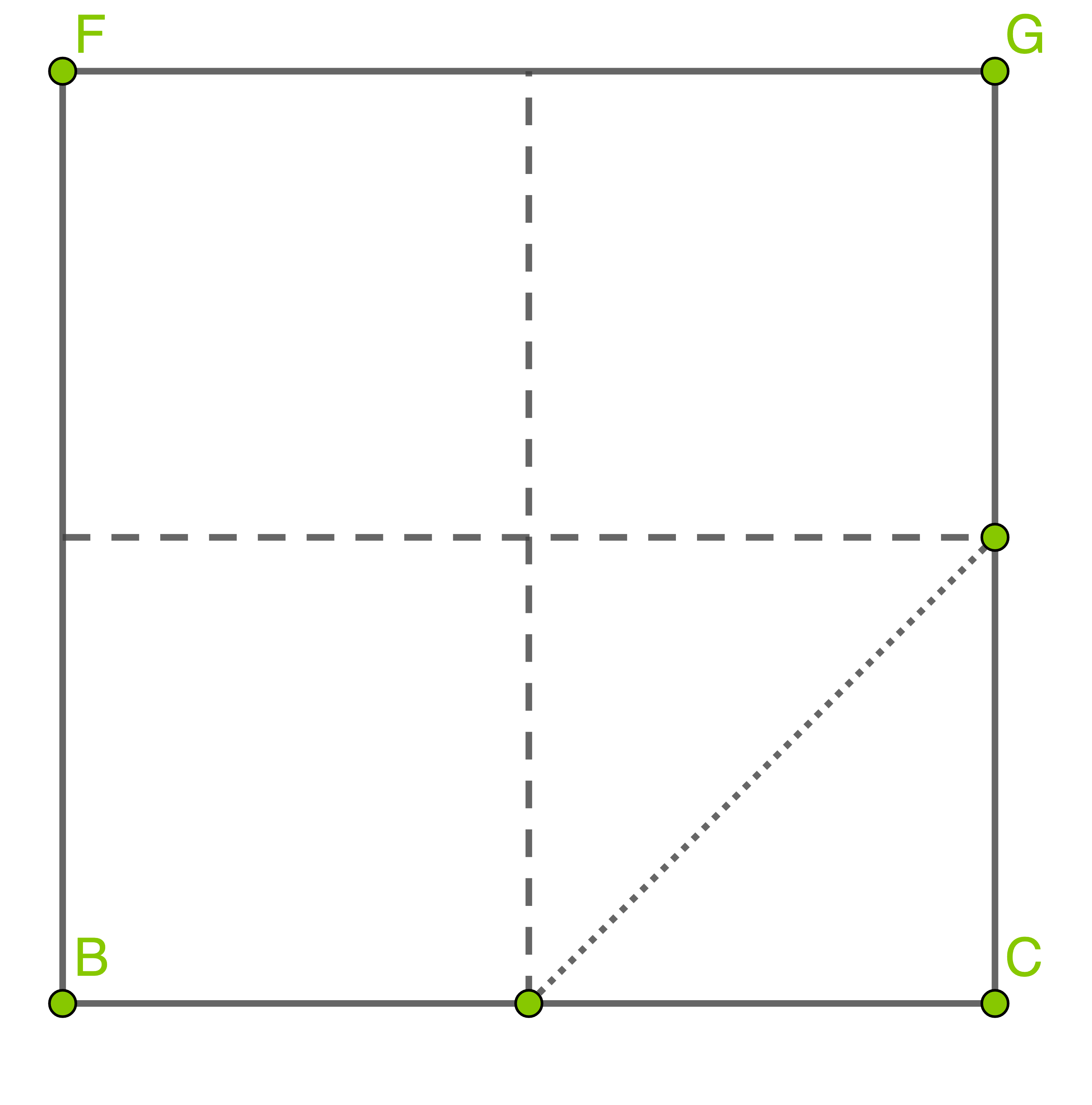
Bergründe mithilfe einer Skizze, dass das Volumen des kleineren Teilkörpers ein Achtel des Volumens des Würfels ist.

(5 BE)

Gegeben ist die Schar der Ebenen $x_3=k$ mit $k\in\mathbb{R}.$
Gib in Abhängigkeit von $k$ die unterschiedlichen Arten der Figuren an, in denen die Ebenen für $0\lt k \lt 9$ den Würfel schneiden.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung II 1

Mittelpunkt - Schleswig-Holstein Abi 2022 (Analytische Geometrie)

Die Koordinaten ergeben sich aus denen von $A$ und $B:$

$M\left(\frac{11+(-11)}{2}\,\bigg \vert\, \frac{11+11}{2}\,\bigg \vert\, \frac{0+28}{2}\right)$ $= M(0\mid 11\mid 14)$

Die Strecke $\overline{CD}$ ist Teil der Geraden $g_{CD}$ durch $C$ und $D$ mit:

$g_{CD}: \overrightarrow{x} =\overrightarrow{OC}+r \cdot \overrightarrow{C D}$ $=\pmatrix{11 \\ -11 \\ 28}+r \cdot\pmatrix{-22 \\ 0 \\ -28},$ $r\in \mathbb{R}$

Durch die Punktprobe mit $N$ ergibt sich:

Rechenweg anzeigen

$\pmatrix{-20 \\ 0 \\ -25} = r \cdot\pmatrix{-22 \\ 0 \\ -28}$

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& -20 &=& -22r &\quad \scriptsize\mid\;:(-22)\\[5pt] & \frac{10}{11} &=& r\\[5pt] \text{II}\quad& 0 &=& 0r \\[5pt] & 0 &=& 0 \\[5pt] \text{III}\quad& -25 &=& -28r &\quad \scriptsize\mid\;:(-28) \\[5pt] & \frac{25}{28} &=& r \end{array}$

Die Gleichungen $\text{I}$ und $\text{III}$ stehen also im Widerspruch zueinander, sodass es keinen Wert für $r$ gibt, für den das Gleichungssystem erfüllt ist.

Der Punkt $N$ liegt also nicht auf der Geraden $g_{CD}$ und kann damit inbesondere nicht auf der Strecke $\overline{CD}$ liegen.

Die Länge des Streckenzugs ergibt sich aus den Beträgen der drei einzelnen Verbindungsvektoren:

Rechenweg anzeigen

$l\approx 102,33\,\text{[LE]}$

Mit dem Kreuzprodukt lässt sich ein Normalenvektor von $E$ berechnen. Das Kreuzprodukt kann mit dem Taschenrechner berechnet werden:

$\overrightarrow{AB}\times \overrightarrow{BC} = \pmatrix{-22 \\ 0 \\ 28} \times\pmatrix{22 \\ -22 \\ 0}$ $=\pmatrix{616 \\ 616 \\ 484}=44 \cdot\pmatrix{14 \\ 14 \\ 11}$

Als Normalenvektor kann also der gekürzte Vektor $\vec{n}=\pmatrix{14\\14\\11}$ verwendet werden.

Einsetzen in die allgemeine Ebenengleichung in Koordinatenform und Durchführen einer Punktprobe beispielsweise mit $A$ ergibt:

Rechenweg anzeigen

$e = 308$

Eine Gleichung von $E$ in Koordinatenform lautet also:

$E:\quad 14x_1 + 14x_2 +11x_3 = 308$

Abstand berechnen

Der Abstand eines Punkts zu einer Ebene lässt sich mit der entsprechenden Formel bzw. der Hesseschen Normalenform berechnen:

$d =\left|\dfrac{14 \cdot(-11)+14 \cdot(-11)+11 \cdot 0-308}{\sqrt{14^{2}+14^{2}+11^{2}}}\right|$ $=\dfrac{616}{\sqrt{513}} \approx 27,20$

Bedeutung des Terms begründen

Als Grundfläche der Pyramide $A B C D$ kann die Fläche des Dreiecks $A B C$ betrachtet werden. Ihr Inhalt ist $G=\frac{1}{2} \cdot|\overrightarrow{A B} \times \overrightarrow{B C}|.$ In der Pyramide ist die zugehörige Spitze dann der Punkt $D,$ die Höhe folglich $d$ und das Volumen $\frac{1}{3} \cdot G \cdot d=\frac{d}{6} \cdot|\overrightarrow{A B} \times \overrightarrow{B C}|$ .

Mit dem Normalenvektor $\pmatrix{0 \\ 0 \\ 1}$ der $x_{1} x_{2}$ -Ebene und der Formel für den Schnittwinkel zweier Ebenen ergibt sich

$\cos (\varphi)=\frac{\pmatrix{14 \\ 14 \\ 11}\circ\pmatrix{0 \\ 0 \\ 1}}{\pmatrix{14 \\ 14 \\ 11} \cdot\pmatrix{0 \\ 0 \\ 1}}=\frac{11}{\sqrt{513}}$ und damit $\varphi = \cos^{-1}\left(\frac{11}{\sqrt{513}}\right) \approx 60,94^{\circ}.$

$P_{h}$ liegt auf der $x_{3}$ -Achse im Bereich $0 \lt x_{3} \lt 28$ bzw. innerhalb des Quaders.

Parameterwerte für rechten Winkel bestimmen

Damit bei $P_h$ ein rechter Winkel vorliegt, muss das Skalarprodukt von $\overrightarrow{BP_h}$ und $\overrightarrow{P_hC}$ Null ergeben:

Mit $\overrightarrow{B P_{h}}=\pmatrix{11 \\ -11 \\ h-28}$ und $\overrightarrow{C P_{h}}=\pmatrix{-11 \\ 11 \\ h-28}$ gilt:

Rechenweg anzeigen

$\begin{array}[t]{rll} h_1 &=& 28-11 \cdot \sqrt{2} \\[5pt] h_2 &=& 28+ 11 \cdot \sqrt{2} \end{array}$

Für $h_1 = 28-11 \cdot \sqrt{2}$ und $h_2= 28 +11 \cdot \sqrt{2}$ besitzt das Dreieck $BP_hC$ bei $P_h$ einen rechten Winkel.

Parameterwerte für ein stumpfwinkliges Dreieck angeben

Je näher der Punkt $P_h$ an der Strecke $\overline{BC}$ liegt, desto stumpfer wird der Winkel bei $P_h.$
Da sich für $h_1$ und $h_2$ ein rechter Winkel ergibt, ist das Dreieck $BP_hC$ daher für alle reellen Zahlen $h$ mit $28-11 \cdot \sqrt{2}\lt h\lt 28+11 \cdot \sqrt{2}$ stumpfwinklig.

Lösung II 2

Volumen des Würfels berechnen:

Die Kantenlängen eines Würfels sind alle gleich lang und somit lässt sich das Volumen eines Würfels mit $V_{\text{Würfel}}=a\cdot a\cdot a=a^3$ berechnen.

Kantenlänge $\vert\,\overrightarrow{AB}\,\vert$ berechnen:

$\begin{array}[t]{rll} \bigg\vert\,\overrightarrow{AB}\,\bigg\vert&=& \bigg\vert\,\pmatrix{3\\-3\\3}-\pmatrix{0\\0\\0}\,\bigg\vert \\[5pt] &=& \sqrt{3^2+(-3)^2+3^2}\\[5pt] &=& \sqrt{27} \end{array}$

Volumenberechnung:

$\begin{array}[t]{rll} V_{\text{Würfel}}&=& \left(\sqrt{27}\right)^3 \\[5pt] &=& 81\sqrt{3}\,[VE]\\[5pt] &\approx& 140,30\,[VE] \end{array}$

Das Volumen des Würfels beträgt $81\sqrt{3}\, [VE]$ .

Form des Vierecks $ABGH$ begründen:

Die Merkmale eines Rechtecks sind einerseits, dass alle Innenwinkel rechte Winkel sind, und dass die gegenüberliegenden Seiten gleich lang sind.
Die Kanten $\overline{AB}$ und $\overline{GH}$ und die Seitendiagonalen $\overline{AH}$ und $\overline{BG}$ sind jeweils gleich lang.
Da $\overline{BG}$ auf der Seitenfläche $BFGC$ liegt, steht $\overline{BG}$ senkrecht zu $\overline{AB}$ . Ebenso mit der selben Argumentation steht $\overline{AH}$ senkrecht zu $\overline{GH}$ .
Mit diesen Seitenverhältnissen innerhalb des Würfels ist bewiesen, dass es sich bei $ABGH$ um ein Rechteck handelt.

Rechteck $ABGH$ zeichnen:

Ebenengleichung $L$ in Koordinatenform aufstellen:

Spannvektoren $\overrightarrow{AB}$ und $\overrightarrow{AG}$ aufstellen:

$\begin{array}[t]{rll} \overrightarrow{AB}&=& \pmatrix{3-0\\-3-0\\3-0}\\[5pt] &=& \pmatrix{3\\-3\\3} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{AG}&=& \pmatrix{0-0\\0-0\\9-0}\\[5pt] &=& \pmatrix{0\\0\\9} \end{array}$

Normalenvektor aufstellen:

Ein Normalenvektor $\overrightarrow{n}$ kannst du mit dem Kreuzprodukt von $\overrightarrow{AB}$ und $\overrightarrow{AG}$ berechnen.

$\overrightarrow{n}=\pmatrix{1\\1\\0}$

Vollständige Lösung anzeigen

Normalenform aufstellen und in Koordinatenform umwandeln:

$\begin{array}[t]{rll} L:0&=& \pmatrix{1\\1\\0}\circ \left[\pmatrix{x_1\\x_2\\x_3}-\pmatrix{0\\0\\0}\right] \\[5pt] L:0&=&x_1+x_2\\[5pt] \end{array}$

Eine Gleichung von $L$ in Koordinatenform ist gegeben durch $L: x_1+x_2=0$ .

Größe des Winkels $\varphi$ bestimmen:

Ein Normalenvektor der $x_1x_3$ -Ebene ist gegeben durch $\overrightarrow{n_{x_1x_3}}=\pmatrix{0\\1\\0}$ .

$\varphi= 45^{\circ}$

Vollständige Lösung anzeigen

Der Winkel, den die Ebene $L$ mit der $x_1x_3$ -Ebene einschließt, beträgt $45^{\circ}$ .

Alternative Lösung:

Da $L$ die $x_3$ -Achse enthält und den Winkel halbiert, den die positive $x$ -Achse und die negative $x_2$ -Achse einschließen, beträgt die Größe des gesuchten Winkels $45^{\circ}$ .

Koordinaten des Punktes $F$ bestimmen:

Die Koordinaten des Mittelpunktes $M$ von $\overline{BG}$ sind gegeben durch $M(1,5\mid -1,5\mid 6)$ .

Koordinaten des Punktes $F$ ermitteln:

Die Strecke $\overline{CF}$ steht senkrecht zu der Ebene $L$ .

$\overrightarrow{OF}= \pmatrix{1,5-\dfrac{3 \sqrt{3}}{2}\\-1,5-\dfrac{3 \sqrt{3}}{2}\\6}$

Vollständige Lösung anzeigen

Die Koordinaten des Punktes $F$ liegen bei $F\left(1,5-\dfrac{3\sqrt{3}}{2}\,\bigg \vert \, -1,5-\dfrac{3 \sqrt{3}}{2}\,\bigg \vert \, 6\right)$ .

Volumen des kleineren Teilkörpers erläutern:

Skizze:

Diagramm eines Quadrats mit Punkten F, G, B und C sowie gestrichelten Linien.

Begründung:

Bei dem kleineren Teilkörper handelt es sich um ein Prisma, wessen Grundfläche eine Teilfläche der Seitenfläche $BFGC$ ist. Der Inhalt dieser Teilfläche beträgt ein Achtel des Inhalts der Seitenfläche $BFGC$ . Die Höhe des Prismas stimmt mit der Kantenlänge des Würfels überein.

Damit ist bewiesen, dass das Volumen des kleineren Teilkörpers ein Achtel des Volumens des Würfels ist.

Schnittfiguren erläutern:

Für $0\lt k\leq 3$ und $6\leq k \lt 9$ handelt es sich bei der jeweiligen Schnittfigur um ein Dreieck.
Für $3\lt k \lt 6$ handelt es sich bei der jeweiligen Schnittfigur um ein Sechseck.

(Tipp: Um diese Vorangehensweise zu veranschaulichen, setze die Zahlen von $0-9$ in die gegebene Schar ein und vergleiche die unterschiedlichen Figuren miteinander. Es kann auch helfen sich das Ganze einmal aufzuzeichnen.)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?