Wahlteil A2

Aufgabe A 2.1

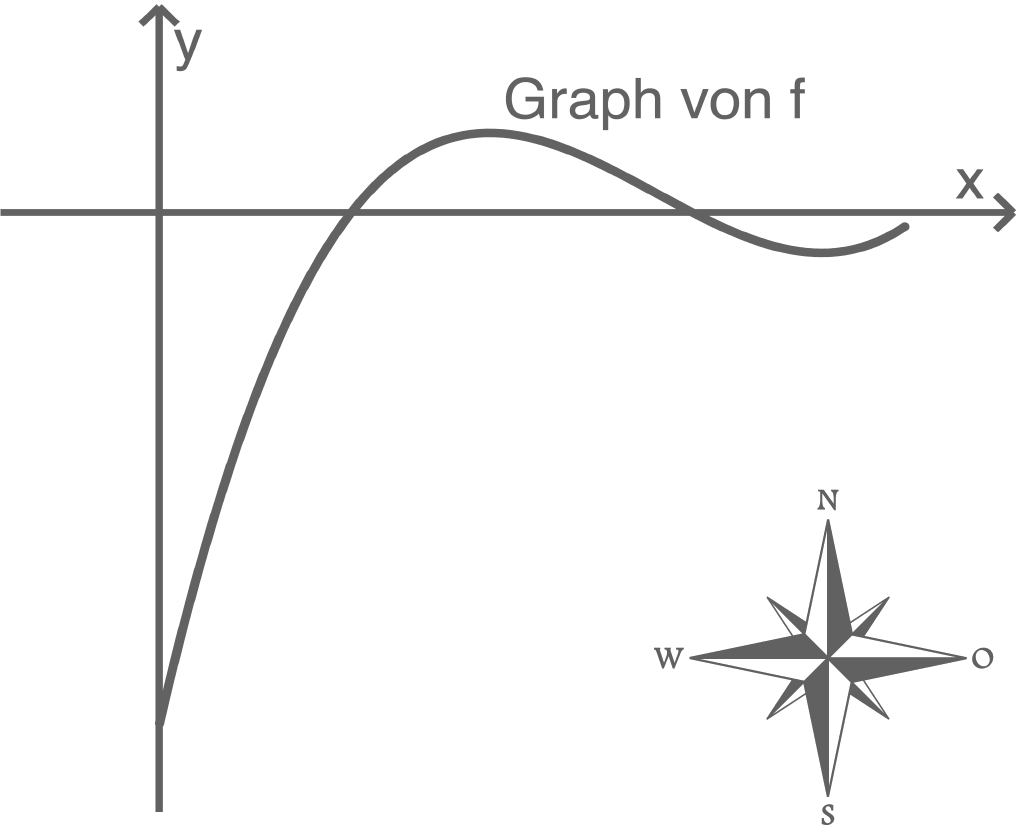
Die Abbildung stellt die Planskizze einer Landstraße dar. Der Verlauf dieser Landstraße wird durch den Graphen der Funktion $f$ mit $f(x)=\dfrac{3}{8} x^3-\dfrac{27}{8} x^2+9 x-\dfrac{13}{2}$ für $0 \leq x \leq \dfrac{9}{2}$ beschrieben.

Die positive $y$ -Achse beschreibt dabei die Himmelsrichtung Norden, die positive $x$ -Achse die Himmelsrichtung Osten.

Eine Längeneinheit im Koordinatensystem entspricht einem Kilometer in der Realität.

Bestimme die Koordinaten des Punkts $P,$ der den nördlichsten Punkt der Landstraße darstellt.

(2,5 VP)

An der Stelle $x_0=3$ wechselt das Vorzeichen der Funktion $\(f$ vom Negativen ins Positive. Beschreibe, was dies für den Verlauf der Landstraße bedeutet.

$($ Teilergebnis: $P(2 \mid 1))$

(1 VP)

Ein Teil des Graphen der Funktion $g$ mit $g(x)=-\dfrac{27}{8} x^2+\dfrac{75}{8} x-\dfrac{13}{2}$ stellt einen Fahrradweg dar, der zwei Punkte der Landstraße verbindet. Diese beiden Punkte werden durch $A(a \mid f(a))$ und $B(b \mid f(b))$ mit $a\lt b$ dargestellt.

Bestimme die Koordinaten von $A$ und $B$ .

(2 VP)

$($ Teilergebnis: $a=0, \; b=1 )$

Berechne $\displaystyle\int_{0}^{1}(g(x)-f(x))\;\mathrm dx$ und interpretiere das Ergebnis im Sachzusammenhang.

(2,5 VP)

Im Folgenden wird auch der Höhenverlauf der Landstraße betrachtet. Stellt $R(r \mid f(r))$ einen Punkt auf der Landstraße dar, so gilt für seine Höhe $h(r):$

$h(r)=u(f(r))$ mit $u(x)=2-\dfrac{1}{500}(x-1)^2$

$( h(r)$ in Kilometer über der Meereshöhe $)$

Zeige, dass der westlichste Punkt der Landstraße auf einer Höhe von etwa 1890 Meter liegt.

(1,5 VP)

Begründe, dass kein Punkt der Landstraße höher als 2000 Meter liegt.

(1,5 VP)

Der am höchsten gelegene Punkt auf der Landstraße wird durch den Punkt $S$ auf dem Graphen von $f$ dargestellt. Bestimme die Koordinaten von $S.$

(1,5 VP)

Zum Abfluss von Regenwasser sind die durch $P(2 \mid 1)$ und $Q(0 \mid f(0))$ dargestellten Punkte auf der Landstraße durch ein geradlinig verlaufendes Rohr verbunden.

Berechne das Gefälle dieses Rohrs.

(3 VP)

Aufgabe A 2.2

Für jedes $a \in \mathbb{R}$ ist eine Funktion $f_{a}$ gegeben durch $f_{a}(x)=\sin \left(\dfrac{\pi}{a^2+1} \cdot x\right).$

Die zugehörigen Graphen werden mit $G_{a}$ bezeichnet.

Berechne die Größe des Steigungswinkels der Tangente an $G_0$ im Ursprung.

(1,5 VP)

Bestimme denjenigen Wert von $a,$ für den die Periode von $f_{a}$ minimal wird.

(1 VP)

Die Tangente an $G_{a}$ an der Stelle $x_0=0$ und die Tangente an $G_{a}$ an der kleinsten positiven Nullstelle von $f_{a}$ schließen mit der $x$ -Achse ein Dreieck ein.

Bestimme alle Werte von $a,$ für die der Inhalt dieses Dreiecks $2,5 \pi$ beträgt.

(3 VP)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung A 2.1

Der nördlichste Punkt der Landstraße entspricht dem Hochpunkt des Graphen von $f.$

1. Schritt: Ableitung bestimmen

$\(f$

2. Schritt: Notwendige Bedingung

$\(\begin{array}[t]{rll} f$

Mit der $abc$ -Formel folgt:

Rechenweg anzeigen

$x_1=2 \; \; \; x_2=4$

Der Abbildung aus der Aufgabenstellung kann entnommen werden, dass der Graph von $f$ an der Stelle $x_1$ ein Maximum annimmt. Auf die Überprüfung der hinreichenden Bedingung kann somit verzichtet werden.

3. Schritt: $y$ -Koordinate bestimmen

$\begin{array}[t]{rll} f(2)&=&\dfrac{3}{8} \cdot 2^3-\dfrac{27}{8} \cdot 2^2+9 \cdot 2-\dfrac{13}{2} & \\[5pt] &=& 1& \\[5pt] \end{array}$

Die Koordinaten des nördlichsten Punkts der Landstraße sind somit gegeben durch $P(2\mid1).$

Bedeutung beschreiben

Der Vorzeichenwechsel der zweiten Ableitung vom Negativen ins Positive beschreibt einen Wechsel von einer Rechtskurve in eine Linkskurve des Graphen von $f.$

Koordinaten bestimmen

Es soll gelten:

$f(x)=g(x)$

Rechnung anzeigen

Mit dem Satz vom Nullprodukt folgt: $x_3=-1, x_4=0$ und $x_5=1$

Da die Funktion $f$ nur für $0 \leq x\leq \dfrac{9}{2}$ definiert ist, ergeben sich die Schnittstellen mit $x_4=0$ und $x_5=1.$

Die $y$ -Koordinaten ergeben sich mit:

$\begin{array}[t]{rll} g(0)&=& -\dfrac{27}{8} \cdot 0^2+\dfrac{75}{8} \cdot 0-\dfrac{13}{2} & \\[5pt] &=& -\dfrac{13}{2}& \\[5pt] g(1)&=& -\dfrac{27}{8} \cdot 1^2+\dfrac{75}{8} \cdot 1-\dfrac{13}{2} & \\[5pt] &=& -\dfrac{1}{2} & \\[5pt] \end{array}$

Die Koordinaten von $A$ und $B$ sind somit gegeben durch $A\left(0 \mid -\dfrac{13}{2}\right)$ und $B\left(1 \mid -\dfrac{1}{2}\right).$

Wert des Integrals berechnen

Rechenweg anzeigen

$\displaystyle\int_{0}^{1}\left(g(x)-f(x)\right)\;\mathrm dx \approx 0,094$

Ergebnis interpretieren

Die Fläche, die von der Landstraße und dem Fahrradweg eingeschlossen wird, hat einen Inhalt von ca. $0,094 \,\text{km} ^2.$

Höhe nachweisen

Die Funktion $f,$ die den Verlauf der Landstraße beschreibt, ist nur für $0 \leq x \leq \dfrac{9}{2}$ definiert. Der westlichste Punkt der Landstraße besitzt somit die $x$ -Koordinate $0.$

Die Höhe dieses Punkts folgt nun mit:

$h(0)= 1,8875 \; [\,\text{km}]$

Rechenweg anzeigen

Somit liegt der westlichste Punkt der Landstraße auf einer Höhe von ca. 1890 Metern.

Begründung

Wegen $(x-1)^2\geq 0$ folgt auch $\dfrac{1}{500}\left(x-1\right)^2 \geq 0.$

Somit gilt: $u(x)=2-\dfrac{1}{500}(x-1)^2 \leq 2$

Daraus folgt nun auch $h(r)=u(f(r))\leq 2.$

Koordinaten bestimmen

Ableitungen bilden:

$\(u$

Notwendige Bedingung:

$\(\begin{array}[t]{rll} u$

Hinreichende Bedingung:

$\(u$

Somit liegt an der Stelle $x=1$ ein Maximum vor.

Wegen $h(r)=u(f(r))$ besitzt die Funktion $h$ für $f(r)=1$ ein Maximum.

Der Punkt $S$ besitzt somit die $y$ -Koordinate $1.$

3. Schritt: $x$ -Koordinate bestimmen

Aus Aufgabenteil a) folgt $f(2)=1.$

Der Punkt $S$ entspricht dem Punkt $P$ und besitzt folglich die Koordinaten $S(2 \mid 1).$

$y$ -Koordinate berechnen:

$\begin{array}[t]{rll} f(0)&=& \dfrac{3}{8} \cdot 0^3-\dfrac{27}{8} \cdot 0^2+9 \cdot 0-\dfrac{13}{2}& \\[5pt] &=& -\dfrac{13}{2} \end{array}$

Höhe der Punkte bestimmen:

$\begin{array}[t]{rll} h(2)&=& u(1) &\\[5pt] &=& 2-\dfrac{1}{500}(1-1)^2&\\[5pt] &=& 2&\\[5pt] \end{array}$

Aus Aufgabenteil c) folgt $h(0)=1,8875.$

Gefälle berechnen:

Rechenweg anzeigen

$\dfrac{h(2)-h(0)}{d(P,Q)} \approx 1,4\,\%$

Das Gefälle des Rohrs beträgt somit etwa $1,4 \,\% .$

Aufgabe A 2.2

Tangentensteigung bestimmen:

$\(\begin{array}[t]{rll} f_0$

$\(\begin{array}[t]{rll} m&=& f_0$

Die Größe des Steigungswinkels folgt mit:

$\begin{array}[t]{rll} \tan (\alpha)&=& m & \\[5pt] \tan (\alpha)&=& \pi &\quad \scriptsize \mid\; \tan^{-1} \\[5pt] \alpha&\approx& 72,3^{\circ} \end{array}$

Für die Periode gilt: $b=\dfrac{2\pi}{p}$

Aus der Funktionsgleichung ergibt sich $b=\dfrac{\pi}{a^2+1}.$ Somit folgt:

$\begin{array}[t]{rll} \dfrac{\pi}{a^2+1}&=& \dfrac{2\pi}{p_a} &\quad \scriptsize \mid\;\cdot p_a \quad \scriptsize \mid\;:\pi \\[5pt] \dfrac{p_a}{a^2+1}&=& 2&\quad \scriptsize \mid\; \cdot (a^2+1)\\[5pt] p_a&=& 2\cdot (a^2+1) & \\[5pt] \end{array}$

Die Periode von $f_a$ wird also für $a=0$ minimal.

Aus dem Verlauf der Sinusfunktion und der Periodenlänge $p_a =2\cdot (a^2+1)$ folgt, dass sich die kleinste positive Nullstelle des Graphen von $f_a$ an der Stelle $x=a^2+1$ befindet.

Somit sind die Punkte $O(0 \mid 0)$ und $P_a(a^2+1 \mid 0)$ Eckpunkte des Dreiecks.

Die Tangente an $G_{a}$ an der Stelle $x_0=0$ und die Tangente an $G_{a}$ an der kleinsten positiven Nullstelle von $f_{a}$ schneiden sich im Punkt $E_a.$ Dieser Punkt ist ein weiterer Punkt des Dreiecks, welcher aufgrund der Symmetrie der Sinusfunkion die $x$ -Koordinate $\dfrac{a^2+1}{2}$ annimmt.

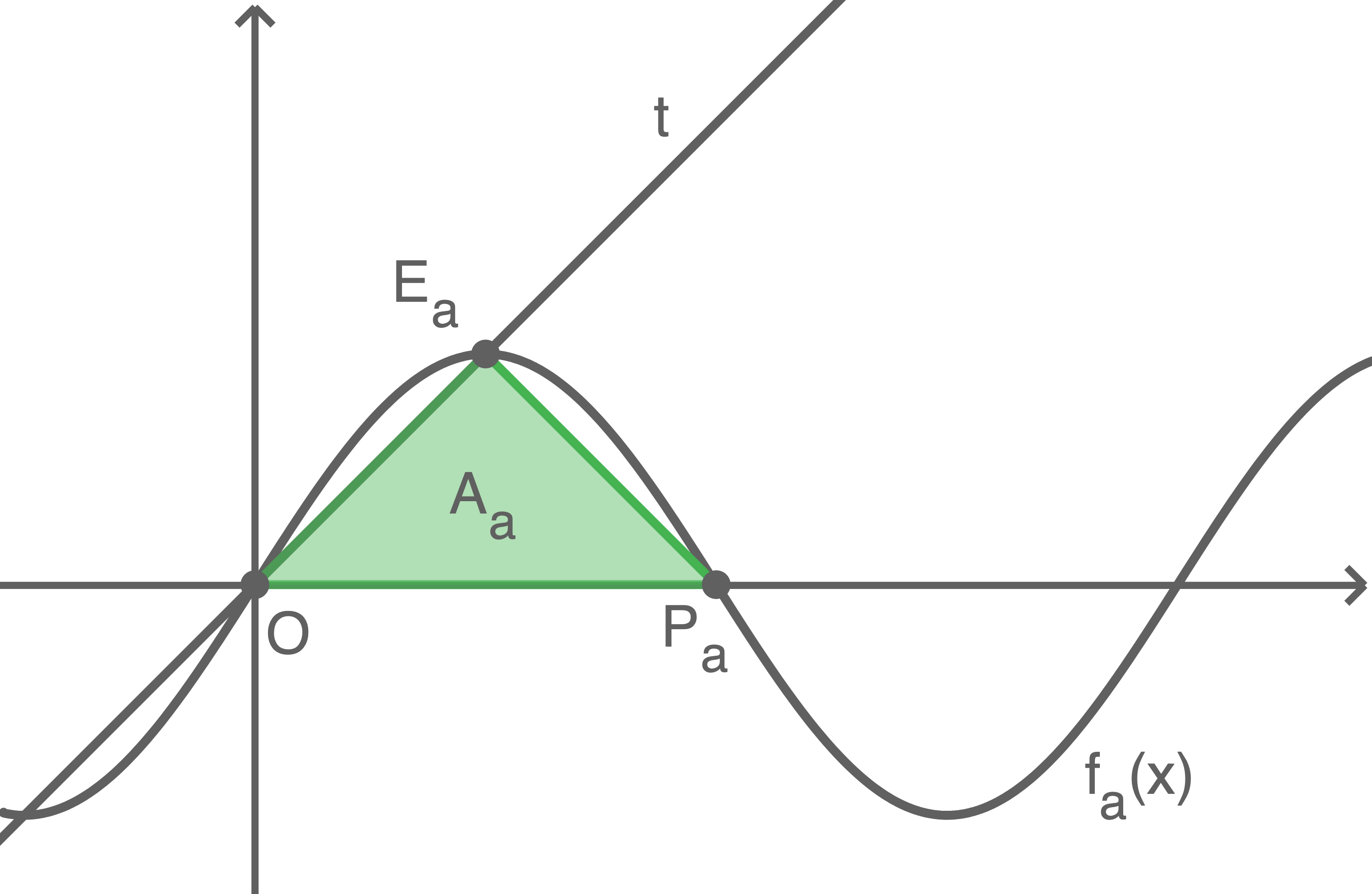
Hilfsskizze Sinusfunktion Dreieck BW Abi 2023

Gleichung der Tangente an den Ursprung bestimmen:

$\(\begin{array}[t]{rll} t: y&=& f_a$

Die $y$ -Koordinate von $E_a$ ergibt sich also mit:

$\begin{array}[t]{rll} y&=& \dfrac{\pi}{a^2+1} \cdot \dfrac{a^2+1}{2} & \\[5pt] &=& \dfrac{\pi}{2} \end{array}$

Der Flächeninhalt $A_a$ des Dreiecks lässt sich nun wie folgt berechnen:

$\begin{array}[t]{rll} A_a&=& \dfrac{1}{2}\cdot |OP_a|\cdot \dfrac{\pi}{2} & \\[5pt] &=&\dfrac{1}{2}\cdot (a^2+1)\cdot \dfrac{\pi}{2}& \\[5pt] &=& \dfrac{\pi}{4}\cdot (a^2+1) \; [\text{FE}]& \\[5pt] \end{array}$

Es soll nun gelten:

$\begin{array}[t]{rll} A&=& 2,5 \pi& \\[5pt] \dfrac{\pi}{4}\cdot (a^2+1)&=& 2,5 \pi&\quad \scriptsize \mid\; \cdot 4 \quad \scriptsize \mid\; : \pi\ \\[5pt] a^2 +1&=& 10 &\quad \scriptsize \mid\; -1\\[5pt] a^2&=& 9 & \\[5pt] a&=& \pm 3 & \\[5pt] \end{array}$

Für $a_1=-3$ und $a_2=3$ beträgt der Flächeninhalt des Dreiecks somit $2,5 \pi.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?