Wahlaufgaben (W1-W6)
W1
Gegeben ist die in  definierte Funktionenschar
definierte Funktionenschar  mit
mit  ;
;  .
.
a)
Zeige, dass  die erste Ableitung von
die erste Ableitung von  ist.
ist.
(2 BE)
b)
Untersuche, für welche Werte des Parameters  der Graph von
der Graph von  eine waagerechte Tangente besitzt.
eine waagerechte Tangente besitzt.
(3 BE)
W2
a)
Für eine Funktion  gilt:
gilt: 
Bestimme die Extremstellen des Graphen von
Bestimme die Extremstellen des Graphen von
(3 BE)
b)
Eine ganzrationale Funktion  hat die Nullstellen
hat die Nullstellen 
 und
und 
Für gilt außerdem:
gilt außerdem:  und
und 
Gib eine Funktionsgleichung für an.
an.
Für
Gib eine Funktionsgleichung für
(2 BE)
W3
Gegeben sind der Punkt  und die Ebene
und die Ebene 
 mit
mit  und
und  gegeben.
gegeben.
a)
Gib eine Gleichung der Gerade  an, die durch den Punkt
an, die durch den Punkt  und senkrecht zu
und senkrecht zu  verläuft.
verläuft.
Zusätzlich ist die Schar der Geraden
(2 BE)
b)
Zeige, dass es genau einen Wert für  gibt, so dass die zugehörige Gerade
gibt, so dass die zugehörige Gerade  parallel zu
parallel zu  ist und nicht in
ist und nicht in  liegt.
liegt.
(3 BE)
W4
Gegeben sind die Punkte  und
und  Gib die Koordinaten des Mittelpunktes der Strecke
Gib die Koordinaten des Mittelpunktes der Strecke  an und bestimme eine Gleichung derjenigen Mittelsenkrechten von
an und bestimme eine Gleichung derjenigen Mittelsenkrechten von  die parallel zur
die parallel zur  -Ebene verläuft.
-Ebene verläuft.
(5 BE)
W5
Die Abbildung zeigt den Graphen der Dichtefunktion der normalverteilten Zufallsgröße 
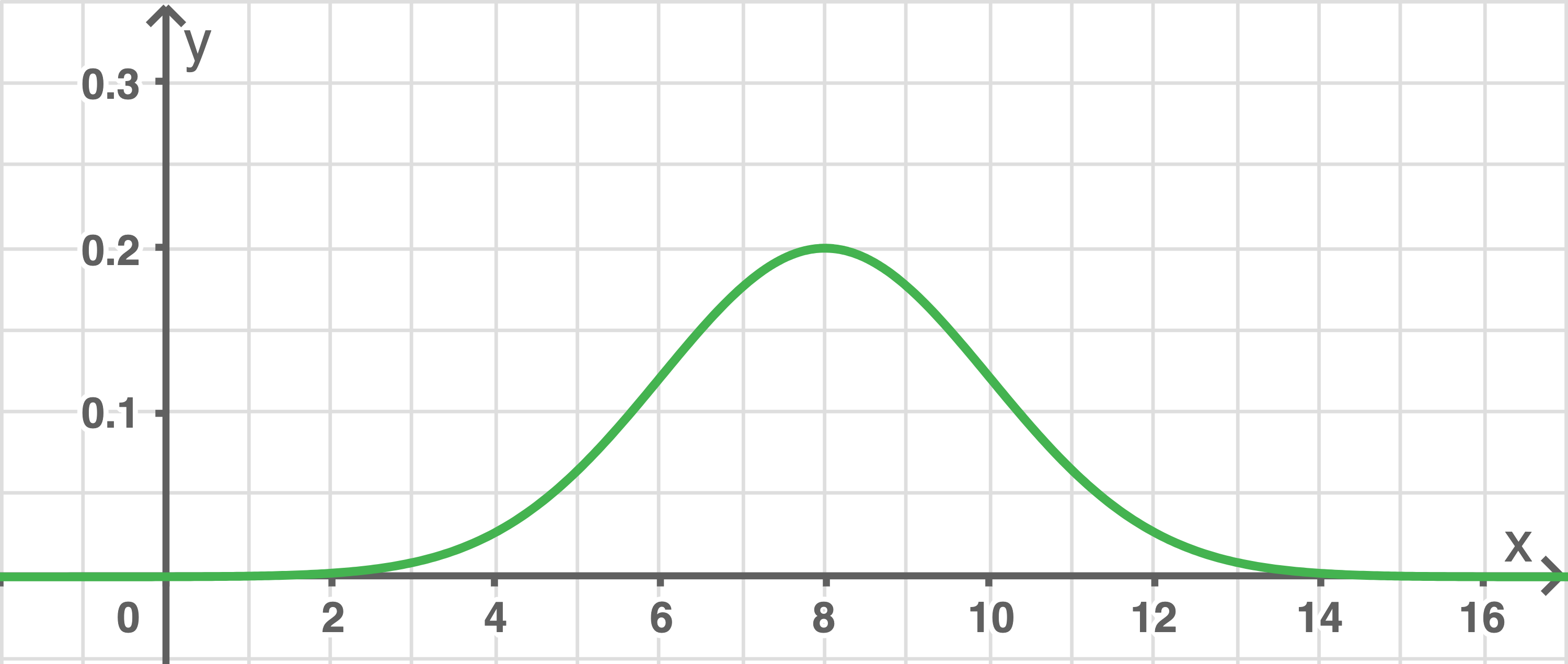

a)
Die Wahrscheinlichkeit dafür, dass  einen Wert aus dem Intervall
einen Wert aus dem Intervall ![\([6;10]\)](https://mathjax.schullv.de/0ab277b497c2e66caf6452b44aee8fe815cb9237a1eeea5d2e9a8b2637e1e3d5?color=5a5a5a) annimmt, beträgt etwa
annimmt, beträgt etwa 
Berechne die Wahrscheinlichkeit dafür, dass einen Wert annimmt, der größer als
einen Wert annimmt, der größer als  ist.
ist.
Berechne die Wahrscheinlichkeit dafür, dass
(2 BE)
b)
Die Zufallsgröße  ist ebenfalls normalverteilt. Der Erwartungswert von
ist ebenfalls normalverteilt. Der Erwartungswert von  ist ebenso groß wie der Erwartungswert von
ist ebenso groß wie der Erwartungswert von  die Standardabweichung von
die Standardabweichung von  ist größer als die Standardabweichung von
ist größer als die Standardabweichung von 
Skizziere in der Abbildung einen möglichen Graphen der Dichtefunktion von
Skizziere in der Abbildung einen möglichen Graphen der Dichtefunktion von
(3 BE)
W6
In einem Gefäß befinden sich schwarze (s) und weiße (w) Kugeln. Ohne Zurücklegen wird zweimal nacheinander genau eine Kugel gezogen. Für das Zufallsexperiment gilt das untenstehende unvollständige Baumdiagramm.
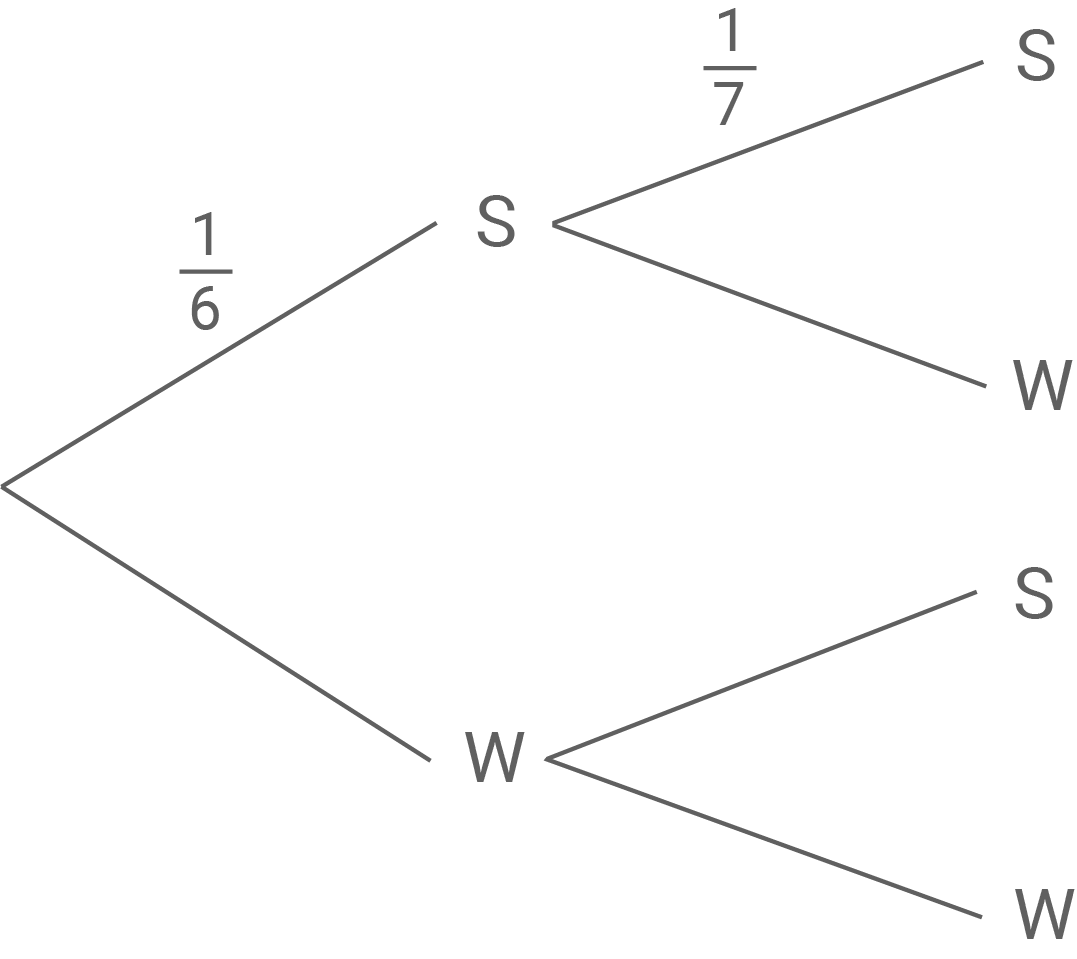

a)
Berechne die Wahrscheinlichkeit dafür, dass mindestens eine weiße Kugel gezogen wird.
(1 BE)
b)
Ermittle die Anzahl der weißen und der schwarzen Kugeln, die sich vor dem Ziehen im Gefäß befanden.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
W1
a)
b)
W2
a)
1. Schritt: Notwendiges Kriterium
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/4e6dbb02eb82d86bf19e631f248badc536cbc08fa1787991d26b2b295bca8b4d?color=5a5a5a) Anwenden der pq-Formel ergibt:
Anwenden der pq-Formel ergibt:
![\(\begin{array}[t]{rll}
x_{1,2} &=& - \dfrac{-2}{2} \pm \sqrt{\left( \dfrac{-2}{2} \right)^2 - (-24)} \\[5pt]
x_{1,2} &=& 1 \pm 5
\end{array}\)](https://mathjax.schullv.de/9a2766074e40f95c556f919c39da6af8fa45d1b0ccea7692d20309b5cf61d9c5?color=5a5a5a) Somit ist
Somit ist  und
und  2. Schritt: Hinreichendes Kriterium
2. Schritt: Hinreichendes Kriterium
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/3729eb20d877dfa6178f81d86267c327fb3d1b4d75d170cc301c0a64afb6ca3b?color=5a5a5a) Folglich gibt
Folglich gibt  die Stelle eines Hochpunkts und
die Stelle eines Hochpunkts und  die Stelle eines Tiefpunkts an.
die Stelle eines Tiefpunkts an.
b)
W3
a)
Die Gerade  besitzt als Richtungsvektor den Normalenvektor von
besitzt als Richtungsvektor den Normalenvektor von 

b)
Der Richtungsvektor von  muss senkrecht zum Normalenvektors von
muss senkrecht zum Normalenvektors von  sein:
sein:

 also
also  Die Punktprobe von
Die Punktprobe von  mit
mit  ergibt:
ergibt:
 Damit ist ausgeschlossen, dass
Damit ist ausgeschlossen, dass  in
in  liegt.
Somit ist gezeigt, dass es genau ein
liegt.
Somit ist gezeigt, dass es genau ein  gibt.
gibt.
W4
W5
a)
Der Graph der Dichtefunktion ist symmetrisch zu  Daher gilt:
Wegen der Symmetrie gilt
Daher gilt:
Wegen der Symmetrie gilt  Folglich beträgt die Wahrscheinlichkeit dafür, dass
Folglich beträgt die Wahrscheinlichkeit dafür, dass  einen Wert annimmt, der größer als 10 ist
einen Wert annimmt, der größer als 10 ist 
b)
In grün ist der ursprüngliche Graph dargestellt, in grau der Graph einer möglichen Dichtefunktion von 
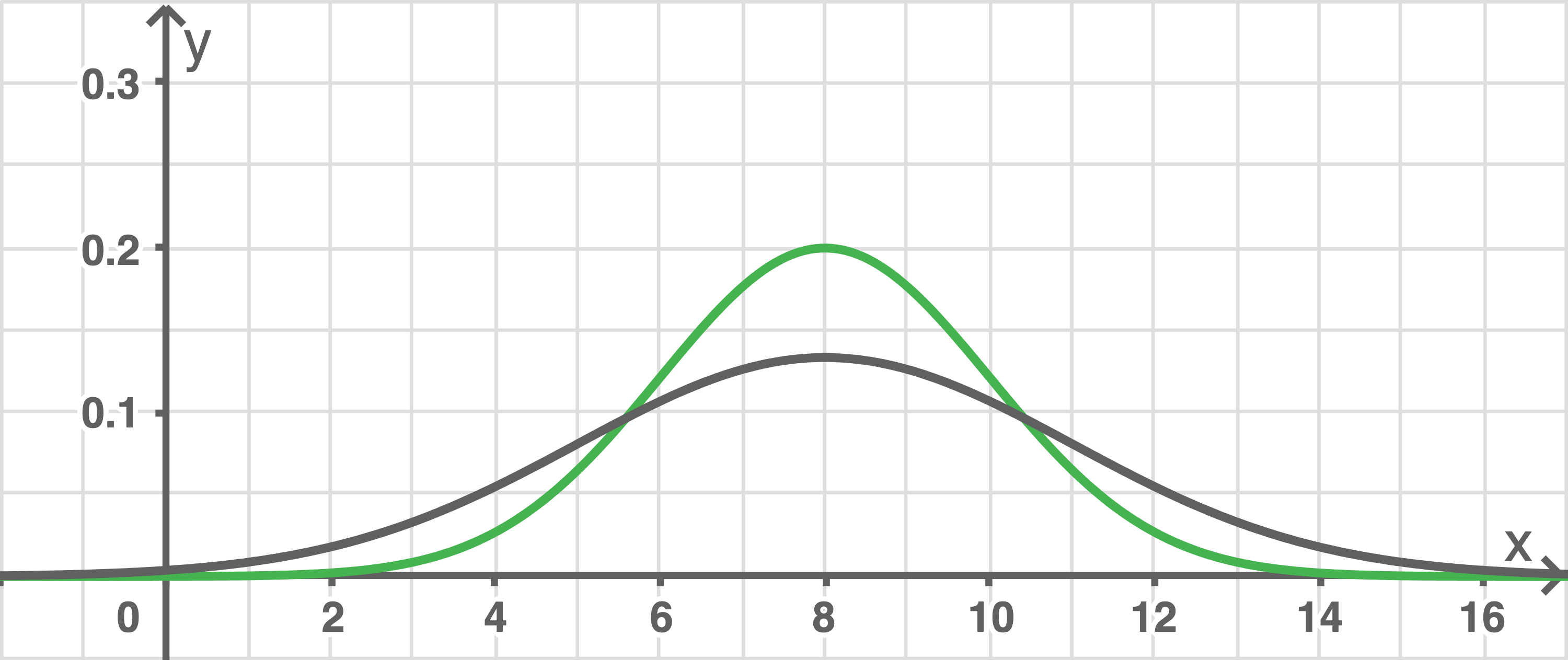

W6
a)
Das Gegenereignis von „mindestens eine weiße Kugel“ ist „zwei schwarze Kugeln“. Die gesuchte Wahrscheinlichkeit ergibt sich also mit der Pfadmultiplikationsregel wie folgt:

b)
Mit den Angaben aus dem Baumdiagramm muss folgendes gelten: